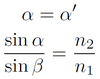Reflexion und Brechung von Mikrowellen
| Reflexion und Brechung von Mikrowellen | |
 Grundaufbau der Experimente mit verwendeten Geräten | |
| Kurzbeschreibung | |
|---|---|
| Mittels eines Mikrowellensenders und einer E-Feld-Sonde wird die Brechung und Reflexion von Mikrowellen untersucht. | |
| Kategorien | |
| Elektrizitätslehre, Optik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Felder |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, Schülereinzelexperiment, Schülergruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Matthias Wegen |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Stephan Pfeiler |
Die im Rahmen dieses Beitrages vorgestellten Experimente übertragen die aus der Lichtoptik bekannten Phänomene der Brechung und Reflexion auf die Ausbreitung von Mikrowellen. Dabei zeigt sich, dass die bekannten Gesetze zur Beschreibung dieser Phänomene für beide Abschnitte des elektromagnetischen Spektrums gelten, wenn die Versuchsanordnungen und Geräte entsprechend angepasst werden. Insbesondere wird ein Versuchsaufbau vorgestellt, der das Brechungs- und Reflexionsgesetz der Lichtoptik für Mikrowellen bestätigt und darüber hinaus die fokussierende Wirkung einer für Mikrowellen modifizierten Sammellinse zeigt.
Inhaltsverzeichnis
Didaktischer Teil
Begründung der Themenwahl
Die kontrollierte Verwendung von elektromagnetischen Wellen, sowohl natürlicher als auch künstlich erzeugter Quellen, stellt einen Grundpfeiler des Zusammenlebens unserer modernen Gesellschaft dar. Mikrowellen werden dabei vorrangig in der Nachrichtentechnik angewandt, wo sie hauptsächlich zur Übertragung von Informationen verwendet werden (vgl. Bundesnetzagentur[1]) . In Großgeräten wie Teilchenbeschleunigern werden sie zur Beschleunigung von Teilchen eingesetzt (vgl. Wille[2]), um das Standardmodell der Teilchenphysik zu überprüfen oder neue Theorien zu falsifizieren. Das wohl bekannteste Beispiel für den Einsatz von Mikrowellen im Alltag ist der Mikrowellenherd, der Speisen und Getränke aufgrund der Absorption von Mikrowellen erwärmt. Neben der gegebenen Gegenwartsbedeutung und Zugänglichkeit besitzen Mikrowellen eine exemplarische Bedeutung, Konzepte und Eigenschaften elektromagnetischer Wellen zu verdeutlichen. Von Vorteil ist dabei, dass Mikrowellen aufgrund ihrer Wellenlänge von 300 mm bis 1 mm kurzwellig genug sind, um störende Phänomene wie Beugung und Interferenz (siehe Interferenz von Mikrowellen) zu vernachlässigen, anderseits langwellig geung sind, um Wellenphänomene wie Stehwelligkeit zu zeigen (vgl. Tipler/Mosca[3], siehe auch Wellenlänge stehender Mikrowellen ).
Ziel/Motivation
Die Phänomene der Brechung und Reflexion werden im Kontext der Lichtoptik in der Grundschule eingeführt und in der Sekundarstufe I ausführlich behandelt (vgl. Rahmenlehrplan Sek I[4]). Daraus ergibt sich das bekannte Brechungsgesetz nach Snellius und das Reflexionsgesetz. In der Sekundarstufe II wird die Wellenoptik eingeführt, die häufig aus einem Konflikt zur bereits erlernten Lichtoptik heraus generiert wird (vgl. Rahmenlehrplan Sek II[5]). Als Beispiel sei hier das Phänomen der Beugung genannt, dass nicht mit dem aus der Lichtoptik bekannten Strahlenmodell erklärt werden kann. In den meisten Curricula werden zwar die neuen Phänomene der Wellenoptik (Beugung, Interferenz, Polarisation, Absorption) ausführlich behandelt, aber häufig ein Rückschluss auf die Gesetze der Lichtoptik verpasst. So ist den Schülern nicht klar, dass auch Wellen der Reflexion und Brechung gehorchen und wie dieser Vorgang physikalisch begründet werden kann. Allenfalls stellt sich ein intuitives Verständnis dieser physikalischen Vorgänge ein, dass keinesfalls als gesichert angenommen werden kann. Ziel der vorgestellten Versuche ist es, diese Trennung zwischen Wellen- und Lichtoptik aufzulösen und ein Transfer zwischen beiden Disziplinen herzustellen. Es zeigt sich, dass die erlernten Methoden und Konzepte aus der Lichtoptik weiterhin verwendet werden können, wenn Modifizierungen in der Auswertung und Darstellung der Ergebnisse durchgeführt werden.
Physikalische Grundlagen
Für die Versuche wird das aus der Lichtoptik bekannte Reflexions- und Brechungsgesetz benötigt (siehe Abbildung rechts). Dabei ist der Winkel des einfallenden Strahls, der Winkel des reflektierten Strahls bezüglich eines senkrecht auf der reflektierenden Fläche stehenden Lotes. Einfallender und reflektierter Strahl liegen mit dem Lot in einer Ebene und sind beide gleich groß. Bei der Brechung gibt den Winkel des gebrochenen Strahls bezüglich des Lotes an. Die optische Dichte der verschiedenen Medien wird mit bzw. bezeichnet (vgl. Nolting[6]). Je nachdem, wie das Verhältnis der optischen Dichten zueinander ist, fällt die Brechung stärker oder schwächer aus. Der Grenzfall der Totalreflexion wird in diesem Beitrag nicht betrachtet.
Versuchsanleitung
Verwendete Geräte
- Mikrowellen-Quelle (Gunn+Hornantenne)
- E-Feld-Sonde
- DC-V-Messgerät
- Optische Bank (mit diversen Aufsätzen zur Fixierung der Geräte)
- Reflexionsschirm[7]
- Sammellinse[8]
- Halbzylinder mit Winkelskale[8]
- Quarzsand
- diverse Kabel
Versuchsaufbau
Das Experiment besteht aus einen grundlegenden Aufbau, der je nach Versuch modifiziert werden kann. Zentrum des Aufbaus stellt die optische Bank dar, auf der alle benötigten Geräte montiert werden. Die Erzeugung der Mikrowellen wird durch ein Gunn-Element realisiert, das die Strahlung über Hohlraumresonator und Hornantenne mit einer Frequenz von 9,4 MHz [9] und einer typischen Abstrahlcharakteristik aussendet (siehe Abstrahlcharakteristik Mikrowellensender). In ausreichendem Abstand (Fernfeld, d= 400 mm)[10] kann die Strahlung als ebene Welle modelliert werden. Die Messung der Strahlung erfolgt über eine E-Feld-Sonde, die die elektrische Komponente des Feldes parallel zur Achse der Sonde misst. Das Signal wird gleichgerichtet, wobei aufgrund der nichtlinearen Diodenkennlinie von einer quadratischen Proportionalität zwischen Feldstärke und Spannung ausgegangenen werden kann. Mikrowellen-Quelle und E-Feld-Sonde sind so auszurichten, dass die Wellennormale der Mikrowellen orthogonal zur Achse der E-Feld-Sonde steht. So wird sichergestellt, dass die E-Feld-Sonde das maximale Signal anzeigt. Bei allen Versuchen muss sichergestellt werden, dass die E-Feld-Sonde das Hauptmaximum der Abstrahlcharakteristik misst, sowohl in horizontaler als auch in vertikaler Richtung. Zwischen Mikrowellen-Quelle und E-Feld-Sonde werden die jeweiligen Geräte zur Untersuchung der lichtoptischen Phänomene eingebracht. Es ist darauf zu achten, dass sich alle Geräte in einer Ebene befinden (optische Mittelebene), um einen optimalen Strahlengang zu ermöglichen.
Sicherheitshinweis
Die von der Mikrowellen-Quelle ausgesandte Strahlung weist eine nur geringe Leistung von 10 mW auf. Trotzdem sollte es vermieden werden, direkt in den aktiven Hornstrahler zu schauen. Eine Bestrahlung über längeren Zeitraum kann zu einer Beeinträchtigung der Sehleistung führen (vgl. ICNIRP[11]).
Versuch I (Brechungsgesetz)
In diesem Versuch wird zwischen Mikrowellen-Quelle und E-Feld-Sonde der Halbzylinder mit Winkelskale eingebracht. Dabei befindet sich die E-Feld-Sonde auf einem drehbaren Arm, in dessen Drehachse der Halbzylinder ruht. Wird der Zylinder um seine Achse gedreht, so verändert sich der Winkel, unter dem die Mikrowellen aus dem Halbzylinder austreten. Bei dem Übergang an der ebenen Grenzfläche zwischen Halbzylinder und Luft findet die Brechung statt. Mit der E-Feld-Sonde wird derjenige Winkel gesucht, unter dem das Maximum des Signals zu finden ist. Wenn in den Halbzylinder Quarzsand eingefüllt wird, lässt sich aus einer Messreihe mit mehreren Winkeln sowohl das Brechungsgesetz überprüfen, als auch die Brechzahl von Quarzsand berechnen.
Versuchsdurchführung
Mikrowellen-Quelle, E-Feld-Sonde und Halbzylinder werden in der optischen Mittelebene ausgerichtet. Es ist darauf zu achten, dass sich der Halbzylinder im Fernfeld der Mikrowellen-Strahlung befindet. Der Versuchsaufbau wird so ausgerichtet, dass die E-Feld-Sonde unter einem Winkel von 0° das Hauptmaximum anzeigt. Anschließend wird eine Messreihe im unbefülltem Zustand aufgenommen, um den systematischen Fehler der Versuchsanordnung zu untersuchen. Dafür werden für verschiedene Winkel des Halbzylinders die Hauptmaxima der Strahlung untersucht. Es empfiehlt sich, den Halbzylinder über seine gesamte Ausdehnung zu vermessen. Nun kann mit der Untersuchung der Brechung begonnen werden, wozu der Halbzylinder gleichmäßig mit Quarzsand gefüllt wird. Um den korrekten Strahlengang zu überprüfen, wird sowohl der Winkel am Halbzylinder als auch an der E-Feld-Sonde auf 0° gestellt. In dieser Position muss das Hauptmaximum gemessen werden. Ist dies nicht der Fall, muss die horizontale und vertikale Ausrichtung des Versuchsaufbaus korrigiert werden. Um das Brechungsgesetz zu überprüfen, wird nun der Winkel an dem Halbzylinder variiert und anschließend der Winkel bestimmt, unter dem die E-Feld-Sonde das Hauptmaximum der Strahlung misst. Beide Winkel werden notiert.
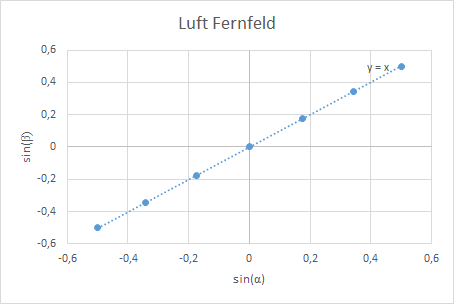
Brechung an Luft
|
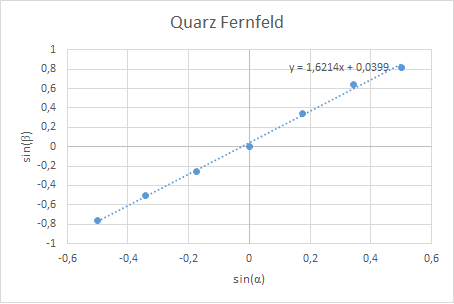
Brechung an Quarz
|
Versuchsauswertung
Die Ergebnisse der zwei Messreihen können in einem Diagramm dargestellt werden. Dazu wird von den gemessenen Winkeln der Sinus gebildet. Lässt sich zwischen Einfalls- und Ausfallswinkel ein linearer Zusammenhang generieren, so ist das Brechungsgesetz gültig. Der Anstieg der Regressionsgeraden gibt den Brechungsindex des jeweiligen Mediums an. Für Luft beträgt er , für Quarzsand rund . Dieses Ergebnis deckt sich mit einem geringen Fehler von unter 10 % mit der Vorgabe von [8]. Die Ungenauigkeit kommt dadurch zu Stande, dass nur mit einer Winkelauflösung von 5° gemessen werden konnte und nicht wie vom Hersteller vorgegeben mit einer Auflösung von 2°.
Versuch II (Sammellinse)
In diesem Versuch soll die fokussierende Wirkung einer Sammellinse auf Mikrowellen untersucht werden. Dazu wird eine mit Quarzsand befüllte Sammellinse zwischen die Mikrowellen-Quelle und die E-Feld-Sonde eingebracht. Die Sammellinse besteht aus zwei sphärischen PVC-Schalen, die an einer gemeinsamen Sehne zusammengefügt sind. Sie lässt sich mit Quarzsand befüllen, so dass die Mikrowellen beim Durchgang durch die Sammellinse gebrochen werden. Die Brechung fällt umso stärker aus, je weiter die Strahlen von der Mittelachse der Linse entfernt sind, was als fokussierende Wirkung bezeichnet wird. Wird davon ausgegangen, dass die Mikrowellen-Quelle ebene Wellen als Parallelstrahlen aussendet, werden die Strahlen nach Durchgang durch die Sammellinse im Brennpunkt fokussiert. Um diesen Effekt zu überprüfen, wird die Halbwertsbreite der Strahlung in einem festgewählten Abstand zuerst ohne Sammellinse gemessen und danach mit der Halbwertsbreite der Strahlung nach Durchgang durch die Sammellinse verglichen.
Versuchsdurchführung
Mikrowellen-Quelle, E-Feld-Sonde und Sammellinse werden in der optischen Mittelebene ausgerichtet. Der Abstand zwischen Mikrowellen-Quelle und Sammellinse sollte mindestens 400 mm betragen, um die ausgehenden Strahlen erst im Fernfeld zu brechen. Die E-Feld-Sonde wird in der Brennebene der Sammellinse positioniert, die in einem Abstand von ca. 160 mm liegt [8]. Die Messung der Halbwertsbreite ohne Sammellinse sollte also in einem Abstand von ca. 560 mm durchgeführt werden. Dazu wird die E-Feld-Sonde transversal zur Ausbreitungsrichtung der Mirkowellen verschoben, bis das Maximum gefunden ist. Der Wert des Maximums wird notiert. Die Verbindungslinie zwischen dieser Stelle und der Mikrowellen-Quelle ist die optische Achse, auf der später die Sammellinse positioniert werden muss. Vorerst wird die Halbwertsbreite gemessen, in dem die E-Feld-Sonde solange transversal verschoben wird, bis die Hälfte des maximal gemessenen Signals angezeigt wird. Die Messung wird in anderer Richtung wiederholt. Sowohl der Wert des Signals als auch der Abstand der beiden Halbwertsbreiten voneinander wird notiert. Die Messung wird wiederholt, nachdem die Sammellinse zwischen Mikrowellen-Quelle und E-Feld-Sonde eingebracht ist. Wieder wird sowohl der Wert des Signals als auch der Abstand der Halbwertsbreiten voneinander notiert.
Halbwertsbreiten ohne Linse
|
Halbwertsbreite mit Linse
|
Versuchsauswertung
Die Halbwertsbreiten und die dabei auftretenden Maxima werden miteinander verglichen. Es zeigt sich, dass die Halbwertsbreite der Strahlung durch die Sammellinse erheblich verringert wird. Es lässt sich auf eine fokussierende Wirkung der mit Quarzsand gefüllten Sammellinse schließen. Dieses Ergebnis wird auch dadurch bestätigt, als dass die Feldstärke der Strahlung im Brennpunkt der Sammellinse erheblicher höher ist als an gleicher Position ohne vorhergehender Brechung in der Sammellinse. Damit wird gezeigt, dass sich der Einsatz optischer Geräte, wie sie aus der Lichtoptik bekannt sind, auch für Mikrowellen realisieren lässt. In diesem Fall muss allerdings auf andere Medien als Glas zurückgegriffen werden, da sonst die Strahlung nicht gebrochen wird. Im Falle von Mikrowellen bietet sich Quarzsand zur Modellierung von Linsen und Prismen an, der in nichtbrechendes Material wie PVC gefüllt wird.
Halbwertsbreiten ohne Linse
|
Halbwertsbreite mit Linse
|
Versuch III (Reflexion)
In diesem Versuch soll die Reflexion von Mikrowellen untersucht werden. Dazu wird zwischen Mikrowellen-Quelle und E-Feld-Sonde eine Metall-Platte eingebracht, die um ihre Achse drehbar ist. Je nachdem, unter welchem Winkel die Mikrowellen auf die Metall-Platte fallen, kann das Hauptmaximum der Strahlung an einem anderen Ort im Raum gemessen werden. Aus dem Vergleich der Winkel von einfallenden und reflektierten Strahlen lässt sich das Reflexionsgesetz überprüfen.
Versuchsdurchführung
Mikrowellen-Quelle und E-Feld-Sonde werden in der optischen Mittelebene ausgerichtet. Wird die Metall-Platte zwischen Quelle und Sonde positioniert, so muss das gemessene Signal auf 0 V fallen. Ist dies nicht der Fall, muss der Versuchsaufbau hinsichtlich weiterer reflektierender Flächen im Raum untersucht werden, die die Mikrowellen ungewollt zur Sonde lenken. Nach der Justierung des Versuchsaufbaus folgt die Messung der Hauptmaxima. Dazu wird zuerst der Einfallswinkel der Strahlung im Bezug zur Flächennormalen der Metallplatte eingestellt und notiert. Mit der E-Feld-Sonde wird nun die Position des Hauptmaximums identifiziert, indem die Sonde durch den Raum bewegt wird. Es empfiehlt sich, die Sonde auf einer Geraden festen Abstandes parallel zur optischen Bank zu bewegen, um reproduzierbare Ergebnisse zu erzielen. Ist das Hauptmaximum gefunden, wird der Winkel notiert und das Vorgehen für weitere Einfallswinkel wiederholt. Zweckmäßige Intervalle sind Winkel zwischen 20° und 70° im Abstand von 10°.
| 1 | 20 | 20 |
| 2 | 30 | 30 |
| 3 | 40 | 40 |
| 4 | 50 | 50 |
| 5 | 60 | 60 |
| 6 | 70 | 70 |
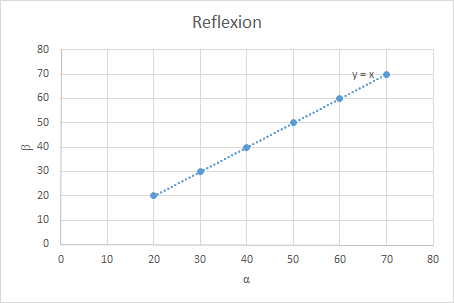
Versuchsauswertung
Die Ergebnisse der Messreihe können in einem Diagramm dargestellt werden. Lässt sich zwischen Einfalls- und Ausfallswinkel ein linearer Zusammenhang generieren, so ist das Reflexionsgesetz gültig. Der Anstieg der Regressionsgeraden sollte dabei 1 betragen. Mögliche Fehler bestehen darin, dass die Metall-Platt nicht komplett eben ist und weitere reflektierende Materialien im Raum die Messung beeinflussen.
Einbringung in den Unterricht
Die langwierigen Vorbereitungen und notwendigen, mehrmaligen Messungen lassen die Versuche ungeeignet für Demonstrationszwecke erscheinen. Einzig die fokussierende Wirkung der Sammellinse kann als Lehrerexperiment dazu dienen, eine Motivation zu schaffen, das Phänomen der Brechung auch bei Mikrowellen zu untersuchen. Denoch ist ein Einsatz als Schülerexperiment einzeln oder in Gruppen denkbar. Die klare Zielsetzung und der modulhafte Aufbau der Experimente bieten eine Öffnung hinsichtlich der Planung und Durchführung einzelner Experimente an. So können zum Beispiel die Winkel zur Überprüfung des Brechungs- bzw. Reflexionsgesetzes von den Schülern selbst bestimmt werden. Sie sind frei in der Wahl der Auflösung als auch des Umfangs der Winkel. Bei der Überprüfung des Reflexionsgesetzes kann es den Schülern überlassen werden, eine Methode zu entwickeln, wie die Reflexionswinkel präzise und reproduzierbar gemessen werden können. Im Rahmen einer Projektarbeit kann der Brechungsindex verschiedener Materialien untersucht werden. Die Durchführung der Experimente kann durch Gruppenarbeit erleichtert werden, in dem eine Arbeitsteilung zwischen den Bereichen Justage und Durchführung, Ablesen der Instrumente und Aufnahme der Ergebnisse stattfindet.
Literatur
- ↑ Bundesnetzagentur (2014): Frequenzplan, verfügbar unter Bundesnetzagentur [05.02.2016]
- ↑ Wille, K. (1996): Physik der Teilchenbeschleuniger und Synchrotronstrahlungsquellen ; Teubner, Stuttgart
- ↑ Tipler, P. A., Mosca G (2009): Physik für Wissenschaftler und Ingenieure; Spektrum Akademischer Verlag, Heidelberg
- ↑ Senatsverwaltung für Bildung, Jugend und Sport (2006): Rahmenlehrplan für Physik, Sekundarstufe I, verfügbar unter Bildungsserver Berlin Brandenburg [05.02.2016]
- ↑ Senatsverwaltung für Bildung, Jugend und Sport (2006): Rahmenlehrplan für Physik, Sekundarstufe II, verfügbar unter Bildungsserver Berlin Brandenburg [05.02.2016]
- ↑ Nolting, W. (2011): Grundkurs Theoretische Physik, Elektrodynamik; Springer, Heidelberg
- ↑ Leybold, Versuch 3.7.4.3, verfügbar im Online-Katalog [05.02.2016]
- ↑ 8,0 8,1 8,2 8,3 Leybold, Versuch 3.7.4.5, verfügbar im Online-Katalog [05.02.2016]
- ↑ Leybold, Versuch 3.7.4.1, verfügbar im Online-Katalog [05.02.2016]
- ↑ Universität Bern, Skriptum zur Vorlesung "Microwavephysics and Quasioptics" 2009, verfügbar im Online-Verzeichnis [05.02.2016]
- ↑ Internationalen Kommission für den Schutz vor nichtionisierender Strahlung (1998), verfügbar unter ICNIRP [05.02.2016]