Messung der Abstrahlcharakteristik eines Mikrowellensenders

Messung der Abstrahlcharakteristik eines Mikrowellensenders
Vermessung der Abstrahlcharakteristik mit Oszilloskop und Lautsprecher
Kurzbeschreibung
Mittels eines Mikrowellensenders und einer E-Feldsonde wird die Abstrahlcharakteristik und die Abstandsabhängigkeit der elektrischen Feldstärke bestimmt.
Kategorien
Elektrizitätslehre
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	Energie
Sonstiges
Durchführungsform	Lehrerdemoexperiment, Schülereinzelexperiment, Schülergruppenexperiment
Anzahl Experimente in dieser Unterkategorie	2
Anspruch des Aufbaus	leicht
Informationen
Name:	Tom Beutler
Kontakt:	${\text{tom.beutler}}$@${\text{gmx.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Franz Boczianowski und Nico Westphal

Eine Mikrowelle ist eine elektromagnetische Welle. Ihre Frequenz liegt im Bereich von 300 MHz bis 300 GHz mit Wellenlängen von 1m bis 1mm. Brechung, Reflexion und Interferenz sind Eigenschaften die allen Wellen gemein sind. Ein deutlicher Unterschied liegt in ihrer Erzeugung. Mikrowellen werden meist als stehende Welle in einem Hohlleiter erzeugt und über eine ausgedehnte Antenne in den freien Raum abgestrahlt. Man unterscheidet hier zwischen dem Nah- und dem Fernfeld. Im Fernfeld kann man den Sender als eine punktförmige Quelle betrachten.

Im beschriebenen Experiment werden wir im Fernfeld die elektrische Feldstärke ${\vec {E}}$ mittels einer E-Feld-Sonde untersuchen. Der Versuch dient der inhaltlichen Erarbeitung der ${\frac {1}{\vec {r}}}$ Abhängigkeit von ${\vec {E}}$.

Um auf die Richtungsabhängigkeit aufmerksam zu machen und die Abstrahlcharakteristik zu bestimmen, messen wir neben der Abstandsabhängigkeit (longitudinaler Feldverlauf) von ${\vec {E}}$ auch die Winkelabhängigkeit in einer Ebene in einem festen Abstand d (transversaler Feldverlauf). Zum besseren Verständnis der Begrifflichkeit siehe auch Leybold, Versuch 3.7.4.1 .

Kurzgefasst: ${\vec {E}}\sim {\frac {1}{\vec {r}}}$

Didaktischer Teil

Die Physik als Wissenschaft zeichnet sich im Vergleich zur Realität dadurch aus, dass häufig Vereinfachungen und Einschränkungen zur Modellierung der Realität vorgenommen werden. Schülern und Studenten soll so die Möglichkeit gegeben werden, schwierige Aufgaben adäquat zu lösen. Dementsprechend müssen auch Bilder, Darstellungen, Grafiken usw. eingesetzt werden, um Probleme und Zusammenhänge einfacher zu gestalten bzw. ein besseres und tieferes Verständnis aufzubauen. Das beschriebene Experiment eignet sich, um die Erstellung, den Umgang und die Interpretation von analogen und logischen Bildern zu trainieren und einen Zusammenhang zwischen ihnen herzustellen.

In einem angeleiteten Schülerexperiment nehmen die Schüler zuerst einige transversale Feldverläufe auf. Sinnvoll ist hier in Abständen von 6, 12, 18, und 24 cm zu messen. Dies kann zum Beispiel in unterschiedlichen Gruppen erfolgen. Das Ziel ist, alle Verläufe in einen Graphen der Funktion (vgl. Abb. 4) über die y-Achse aufzutragen und die Gerade zu identifizieren, auf der die Maxima liegen, sodass im Anschluss die Messung des longitudinalen Feldverlaufs erfolgen kann. Dies verlangt von den Schülern eine hohe kognitive Aufmerksamkeit. Sie müssen zum einen semantisch klar (vgl. Kircher S.219) arbeiten, um die unterschiedlichen Feldverläufe im Nachhinein zu identifizieren. Zum Anderen müssen sie auch syntaktisch klar Einträge vornehmen. Vor allem aber die Fülle an Informationen (vier Feldverläufe mit je 10-20 Messungen) zwingt die Schüler dazu sparsam zu arbeiten. Ist die Gestaltung der Graphen (logische Bilder) abgeschlossen, ist es sinnvoll nach Wainer (aus Kircher S.219) vorzugehen. Als erstes lesen die Schüler die benötigten Einzelwerte (nur Maxima) ab und setzen sie im Anschluss in Relation. Das Verorten der Maxima im Raum aus einem zwei dimensionalen Graphen erfordert eine hohe Vorstellungskraft. Das vorherige Experimentieren dient hier als Unterstützung für schwächere Schüler. Damit wird auch Bruners Lerntheorie (aus Kircher S.126) folge geleistet, dass jeder zu lernende Sachverhalt erst enaktiv (z.B. Experiment) und dann ikonisch (Bild) bearbeitet werden soll.

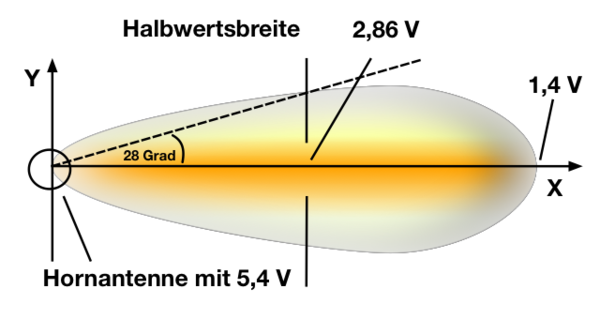
Einen starken Fokus legen wir nun auf die Visualisierung der Abstrahlungskeule. Sie dient als analoge Darstellung dazu, eine Struktur aufzuzeigen, die nicht direkt beobachtbar ist und besitzt vor allem die Gefahr eine Fehlvorstellung hervorzurufen, wie es bei analogen Bildern passieren kann (vgl. Kircher S.218). Schaut man sich das Bild (vgl. Abb. 5) an, so kann man zu der Vermutung kommen, dass die Hornantenne nur im Bereich der Keule abstrahlt und dahinter keine Werte messbar sind. Dies könnte zum einen schon das Wort Abstrahlungskeule suggerieren, zum anderen ist das Verständnis der Darstellung keinesfalls trivial. Die Schüler haben allerdings durch die Messung des longitudinalen Feldverlaufs festgestellt, dass es sehr wohl Werte jenseits der Keule gibt. Um ein tieferes Verständnis aufzubauen, hat man nun folgende Möglichkeiten. Entweder lässt man die Schüler die Orte mit der gleichen Spannung U = 1,4 V ausmessen, was messtechnisch schwieriger sein dürfte, oder man lässt sie aus den Messdaten zum transversalen Feldverlauf (evtl. plus zwei weitere Messreihen) die Keule zeichnen. Zweiteres dürfte kognitiv anspruchsvoller sein, da bei der ersten Methode die Keulenform bereits beim ausmessen nachvollzogen wird, während hier aus einem U-y-Diagramm mit Angaben zu x eine x-y-Abbildung gewonnen werden soll. Egal auf welchem Weg man zum analogen Bild kommt, wichtig ist vor allem eine anschließende Sicherungsphase, in der man auf die Darstellung und seine Funktion eingeht.

Versuchsanleitung

Grundsätzliches zu diesem Versuch

Häufig ist es bei Experimenten sinnvoll, sich im Vorfeld zu überlegen, inwiefern Einflussfaktoren die Güte meiner Ergebnisse beeinflussen und ob ein Einsatz im Unterricht möglich und sinnvoll ist. Beim Arbeiten mit der Hornantenne ist folgendes zu beachten (vgl. auch Leybold, Versuch 3.7.4.1, S.3 Leybold, Versuch 3.7.4.1, verfügbar unter [2] ):

• Durch Reflexion der Mikrowellen an senkrechten Flächen können Messergebnisse leicht verfälscht werden.
• Die Hornantenne ist so zu platzieren, dass sie 4m von reflektierenden Flächen entfernt ist.
• Mit Noppenabsorbern (falls vorhanden) kann ein reflexarmer Messraum gebaut bauen.
• In Kabelschleifen können durch das zeitlich veränderliche Magnetfeld der Mikrowelle Spannungen induziert werden. → Diese sind zu vermeiden.
• Die Versuchsperson beeinflusst die Messergebnisse. → Beim Messen muss sie sich hinter die Hornantenne stellen.

Materialien

Abb. 1: Experimentieraufbau

Folgende Materialien werden für den Aufbau des Experimentes benötigt:

• Gunn-Oszillator mit großer Hornantenne
• Gunn-Versorgung mit Netzteil
• E-Feld-Sonde
• Stativklemme mit Sockel
• Voltmeter DC
• 2 Hochfrequenz-Kabel (HF-Kabel)
• Experimentierkabel

Zusätzlich/Optional

• optische Bänke
• Messschiene
• Kariertes Papier

Aufbau

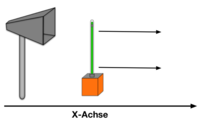
In Abb. 1 sieht man den vollständigen, beschrifteten Aufbau des Versuchs. Die Grundlage ist ein Experimentierset von Leybold. Dort finden sich auch weitere Hinweise zu einem Teil der verwendeten Materialien und zum Aufbau (siehe [3], Leybold, Versuch P3.7.4.1).

Wir beginnen mit dem Mikrowellensender. Zunächst verbinden wir die Hornantenne mit dem Gunn-Oszillator. Im Anschluss nehmen wir eine Stativklemme und befestigen sie an einem Stativ. Nun kann der Mikrowellensender mithilfe der Klemme in Position gebracht werden. Wir beachten dabei, dass die Trichtermündung von der Hornantenne mit der Hochfrequenzdiode der E-Feldsonde auf gleicher Höhe ist (vgl. Abb. 1 links oben). Nur so erzielen wir optimale Ergebnisse.

Die Gunn-Versorgung und den Mikrowellensender können wir nun mithilfe eines Hochfrequenzkabels verbinden (vgl. Abb. 1 rechts oben). An der Gunn-Versorgung wählen wir den beschrifteten "OUT" Ausgang. Am Mikrowellensender steht uns nur ein Eingang zur Verfügung. Im gleichen Zug nehmen wir uns das zweite Hochfrequenzkabel und verbinden die E-Feld-Sonde mit dem "IN" Eingang an der Gunn-Versorgung. Da die E-Feld-Sonde leicht zerbrechlich ist und im Vergleich zum HF-Kabel ein geringes Gewicht aufweist, sollte man darauf achten, dass die Kabel nicht frei hängen.

Im letzten Arbeitsschritt nehmen wir uns zwei Experimentierkabel und verbinden das Voltmeter mit der Gunn-Versorgung. Für Demonstrationszwecke empfehlen wir ein großes analoges Voltmeter, während bei einer genauen Messung ein digitales bevorzugt werden sollte. Das Netzteil kann nun in die Steckdose gesteckt werden.

Es ist zu beachten, dass es keinen Schalter gibt, um die Gunn-Versorgung vom Strom zu trennen, d.h. für Umbau- oder Präzisionsarbeiten muss der Netzstecker aus der Steckdose gezogen werden. Weiterhin sollte vor dem Einschaltvorgang die Sonde aus dem E-M-Feld geführt werden, da die gemessenen Spannungen weit außerhalb des zu messenden Bereiches liegen können.

Durchführung

Zur Messung des E-Feldes verwenden wir die E-Feld-Sonde. Sie misst die elektrische Feldstärke im Mikrowellenfeld punktförmig und gibt uns eine Spannung $U$ an, aus der wir über $U\sim E^{2}$ auf $E$ rückschließen können.

Longitudinaler Feldverlauf

Abb. 2: Messung des longitudinalen Feldverlaufs

Nach dem Einschaltvorgang bewegen wir die E-Feld-Sonde in das elektrische Feld und platzieren sie so, dass sie die Hornantenne berührt. Dies ist der Startpunkt für die Messung. Wir bewegen die Sonde nun entlang einer Geraden von der Hornantenne weg und messen in Abständen von ein bis zwei Zentimeter die Spannung auf einem digitalen Voltmeter ab (vgl. Abb. 2). Die Werte variieren evtl. durch vorhandene Reflexionen leicht, sodass wir kurz warten und den augenscheinlichen Mittelwert aufnehmen. Ab einem Abstand von 40 cm zur Hornantenne können die Abstände auf fünf Zentimeter vergrößert werden. Um zu gewährleisten, dass wir uns auf einer Geraden von der Hornantenne wegbewegen und um den Abstand zu protokollieren, verwenden wir eine Messschiene oder kariertes Papier. Wir beenden unsere Messung in einer Entfernung von einem Meter.

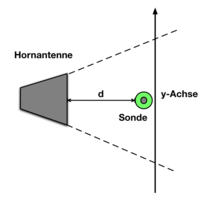
Transversaler Feldverlauf

Abb. 3: Messung des transversalen Feldverlaufs

Nach dem Einschaltvorgang bewegen wir die E-Feld-Sonde in das elektrische Feld und platzieren sie in einem Bereich von d = 10 - 25 cm vor der Hornantenne. Die Winkelabhängigkeit von ${\vec {E}}$ bestimmen wir nun, indem wir die E-Feld-Sonde senkrecht zu d (entlang der y-Achse) in ein Zentimeterschritten verschieben und die Spannung protokollieren (vgl. Abb. 3). Unsere Messung beginnt bei einen Winkel von 0 Grad, hier sollte ein Maximum vorliegen, und endet bei $\pm \alpha _{0}$. $\pm \alpha _{0}$ beschreibt die Winkel, an denen die Spannung null wird. Da wir den Abstand von den 0 Grad in Zentimetern messen, müssen wir den Winkel nicht angeben.

Ergebnisse

Folgende Messwerte wurden aus einer Messkurve mithilfe einer fixierten Messschiene abgelesen und für die Auswertung im folgenden Kapitel verwendet. Für den longitudinalen Feldverlauf wurden 60 Werte aufgenommen, für den transversalen 50 in einer ersten Messung und darauf aufbauend 13 ausgewählte Werte in einer zweiten. Aus Gründen der Übersichtlichkeit beschränken wir uns bei der Tabellenform auf knapp über 30 pro Messung. In den Grafiken sind alle aufgenommenen Werte vorhanden.

Abb. 4: Graph zum Transversalen Feldverlauf

Longitudinaler Feldverlauf ${\text{Abstand}}\ \ x$ [cm] ${\text{Intensität}}$ [V] 0 4,5 2 4,7 4 4,69 6 4,65 8 3,95 10 3,35 12 2,86 14 2,60 16 2,12 18 1,78 20 1,64 22 1,49 24 1,53 26 1,30 28 1,10 30 0,93 32 0,88 34 0,78 36 0,81 38 0,80 40 0,68 45 0,59 50 0,50 55 0,40 60 0,32 65 0,29 70 0,23 75 0,18 80 0,19 85 0,17 90 0,15 95 0,14 100 0,14

Transversaler Feldverlauf ${\text{ y }}\ \$ [cm] ${\text{Intensität 1 im Abstand}}$ ${\text{von 24cm}}$ [V] 0 0 2 0,03 4 0,045 6 0,089 8 0,12 10 0,185 12 0,30 14 0,47 16 0,64 17 0,73 19 0,99 20 1,11 21 1,19 22 1,27 23 1,34 23,5 1,40 24 1,35 25 1,32 26 1,30 27 1,24 28 1,14 29 0,99 30 0,92 31 0,86 32 0,69 34 0,29 36 0,69 38 0,18 40 0,115 42 0,097 44 0,056 46 0,044 47 0,032 49 0

Transversaler Feldverlauf ${\text{ y }}\ \$ [cm] ${\text{Intensität 2 im Abstand}}$ ${\text{von 12cm}}$ [V] 0 0 8 0,05 14 0,29 16 1,20 18 1,85 21 2,53 23,5 2,86 26 2,56 28 1,88 31 1,23 33 0,33 39 0,06 49 0

Auswertung

Quellen für Messunsicherheiten/ -genauigkeit

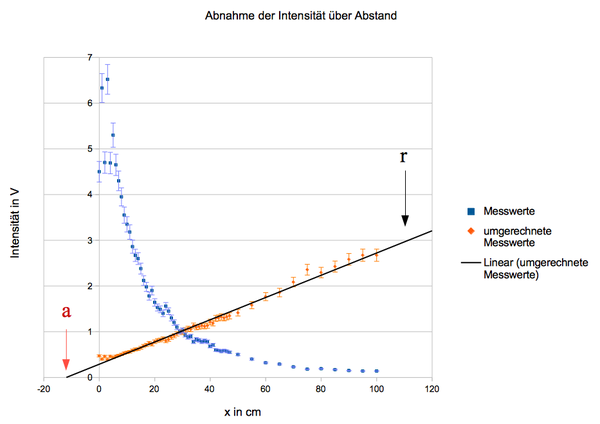
In Abb. 6 sehen wir, dass kurz vor dem Hornstrahler die Messwerte fluktuieren. An dieser Stelle ist der typische Zusammenhang zwischen ${\vec {E}}$ und ${\vec {r}}$ für das Fernfeld nicht feststellbar. Grund hierfür wird sein, dass das Nahfeld über die Hornantenne hinausreicht. Aus den gesammelten Daten entnehmen wir deshalb $U_{0}=5,4V$ als Startwert für das Fernfeld. Diesen benötigen wir im folgenden noch.

Vorhandene Quellen für Messunsicherheiten:

• optische Bank mit Lineal
• digitales Voltmeter
• Person steht beim Messen nicht hinter der Hornantenne
• Gegenstände stehen im Nahbereich

Die letzten beiden Punkte waren aus Platzgründen leider nicht anders durchführbar und hatten den größten Einfluss auf das Experiment. Beispielhaft sieht man dies, wenn man bei obigen Messwerte $U$ bei d=24cm vom longitudinalen mit dem transversalen Feldverlauf vergleicht, die an unterschiedlichen Tagen aufgenommen wurden. Hier stehen sich 1,53 V und 1,4 V gegenüber. Aus diesem Grund wurde der Fehler mit 10% abgeschätzt.

Qualitative Auswertung

Abb. 5: Abstrahlungskeule

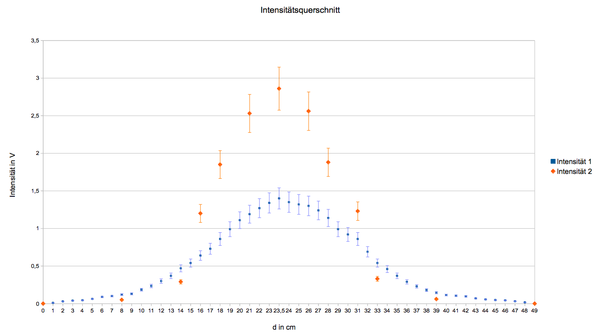
Aus den Daten zum transversalem Feldverlauf können wir entnehmen, dass die gemessenen Spannungen grafisch einer Gauß'schen Glockenkurve ähneln (vgl. Abb. 4). Das E-Feld ist in y-Richtung also nicht konstant. Vielmehr gibt es eine maximale Spannung die auf einer Geraden in x-Richtung liegt.

Obwohl wir nicht radialsymmetrisch von der Hornantenne gemessen haben, sondern in einem Abstand d entlang der y-Achse, können wir folgende Schlussfolgerungen daraus ziehen: 1. Das elektrische Feld ist im Abstand r nicht isotrop (vgl. Abb. 4). 2. Der ${\frac {1}{\vec {r}}}$ Abfall von ${\vec {E}}$ wird nicht bei beliebigen ${\vec {r}}$ beobachtbar sein, sondern ist Richtungsabhängig.

Qualitativ ist es uns nun möglich die Abstrahlungscharakteristik (vgl. Abb. 5) zu beschreiben. Dafür brauchen wir die Definition der Halbwertsbreite $b_{\frac {1}{2}}$: Als Halbwertsbreite bezeichnen wir den Abstand zwischen dem Maximum einer Funktion und dem Wert der Funktion, der die Hälfte des Maximums annimmt. Die Spannungen für die Halbwertsbreite entnehmen wir aus den Graphen (Abb. 4).

	Intensität 1 Abstand 24 cm	Intensität 2 Abstand 12 cm
$U_{max}$	1,40	2,86
${\frac {1}{2}}U_{max}$	0,70	1,43
$b_{\frac {1}{2}}$ links in cm	7,5	6,5
$b_{\frac {1}{2}}$ rechts in cm	8,5	6,5

Die Abstrahlungskeule besitzt an der Hornantenne ein Maximum mit $U_{0}=5,4V$. Auf dieses wenden wir die Definition der Halbwertsbreite an und erhalten ${\frac {1}{2}}U_{0}={\frac {1}{2}}\cdot 5,4V=2,7V$. Wie wir sehen entspricht dieser Wert am ehesten unserem Hochpunkt (aus Intensität 2) mit $U_{12cm}=2,86V$. Den Rand der Abstrahlungskeule erhalten wir, indem wir die Definition der Halbwertsbreite noch einmal anwenden. Wir legen fest, dass $U_{12cm}=2,86V$ unser Extremum ist und erhalten in sehr guter Näherung unser Maximum aus Intensität 1 mit $U_{24cm}=1,4V$. Mithilfe dieser Informationen und der obigen Tabelle, lässt sich der Halbwinkel über der Abstrahlung zu 28 Grad bestimmen (Satz von Phytagoras). Er ist ein Maß für die Abstrahlung im Raum. Umso mehr transversale Feldverläufe aufgenommen werden, umso besser und genauer kann die Abstrahlungscharakteristik gezeichnet werden.

Quantitative Auswertung

Abb. 6: Graph zum longitudinalen Feldverlauf

Mit der qualitativen Auswertung haben wir herausgefunden, dass der ${\frac {1}{\vec {r}}}$ Abfall für ${\vec {E}}$ Richtungsabhängig ist. Zur Verifizierung der Proportionalität zwischen den beiden Größen untersuchen wir die unter Ergebnisse angegebene Messreihe zum longitudinalen Feldverlauf. Zuerst tragen wir die Daten in einen Graph (Abb. 6) ein. Aufgrund der Tatsache, dass $U\sim E^{2}$ und $E^{2}\sim {\frac {1}{r^{2}}}$ gilt, berechnen wir ${\frac {1}{\sqrt {U}}}$. Wir sehen, dass die umgerechneten Werte annähernd eine Gerade beschreiben. Wir führen deshalb eine Regression durch und kommen auf f(x) = 0,024x + 0,288 mit $R^{2}=0,988$. Der Graph Abb. zeigt, dass ${\frac {1}{\sqrt {U}}}$ eine Gerade mit der Nullstelle x = -12 cm ist. Daraus folgt, dass sich das Zentrum der Energieaustrahlung mit der maximalen Energie bei x = -12cm befindet. Aus den Bauteilen des Experimentes haben wir das Zentrum mit -10 cm abgemessen. Unser Ergebnis ist also nicht befriedigend. Im Abschnitt Quellen für Messunsicherheiten/ -genauigkeit haben wir darüber diskutiert, dass sich unmittelbar vor der Hornantenne das Nahfeld befindet. Da im Nahfeld eines Senders keine Zusammenhänge erkennbar sind, haben wir uns dazu entschlossen die Werte an den Stellen x = 0 cm bis x = 4 cm aus der Regression auszuschließen. Wir kommen dadurch auf eine Regressionskurve der Form f(x) = 0,024x + 0,259 mit $R^{2}=0,991$ und einer Nullstelle bei x = -10,8 cm. Für die Energieausstrahlung gilt also ${\frac {1}{\sqrt {U}}}\sim x-a$ mit a = -10,8 cm. Alternativ können wir auch schreiben $U\sim {\frac {1}{(x-a)^{2}}}$. Setzt man $x-a=r$, so folgt $U\sim {\frac {1}{r^{2}}}$ und über die oben genannten Proportionalitäten unsere Aussage.

Die Verbindung von qualitativer und quantitativer Auswertung ergeben somit ${\vec {E}}\sim {\frac {1}{\vec {r}}}$.

Sicherheitshinweise

Von der Firma Leybold wird die Mikrowellenleistung des Gunn-Oszillators mit 10 - 15 mW angegeben. Sie ist somit für Personen ungefährlich. Da Mikrowellen jedoch nicht sichtbar sind und ein Training zur Vorbereitung im Umgang mit Sendern größerer Leistung sinnvoll ist, sollten folgende Regeln in der Schule aufgestellt werden:

• Schaue niemals direkt in die Hornantenne.
• Stelle dich nicht direkt vor die Hornantenne.
• Für Positionierungsarbeiten des Gunn-Oszillators ist der Versuchsaufbau Spannungsfrei zu schalten.