Apps zum Umgang mit Daten und Messunsicherheiten
Kompetenzen für einen adäquaten Umgang mit Messdaten und ihren Unsicherheiten sind beim Experimentieren in der Schule unabdingbar und für den Erkenntnisgewinn in der Physik notwendig. Neben normativen Gründen gibt es mittlerweile eine Reihe von empirischen, fachdidaktischen Studien, welche die Bedeutung von Kompetenzen im Umgang mit Daten unterstreichen: So konnten wir in verschiedenen Studien mit über 1500 Schüler*innen zeigen, dass Schüler*innen, die eher ein hohes Vorwissen haben, eher fachlich richtige Schlüsse aus Messdaten schließen, während hingegen Lernende, denen Kompetenzen zur Auswertung von Messdaten fehlen, eher intuitiv vorgehen und eher zu fachlich falschen Hypothesen gelangen. Vor diesem Hintergrund entwickeln wir im Projekt „Förderung der Argumentationsfähigkeit beim Experimentieren im Physikunterricht“ 10 digitale Lernumgebungen, die das fachliche Wissen der Schüler*innen im Hinblick auf den Umgang mit Daten und Messunsicherheiten fördern und als open educational resource für Physiklehrkräfte zur Einbindung im Unterricht zur Verfügung stehen.
| (A) Direktes Messen | (B) Indirektes Messen |
|---|---|
| (A1) Streuung von Messwerten
Jede Messung ist mit einer Unsicherheit versehen. Zur Angabe eines Messergebnisses gehört stets die Messunsicherheit |
(B1) Addition absoluter Unsicherheiten Verrechnung unsicherheitsbelasteter Größen mit Konstanten und Fortpflanzung von Unsicherheiten in physikalischen Gesetzmäßigkeiten (Strichrechnung) |
| (A2) Unsicherheitsbestimmung
Unsicherheiten können prinzipiell auf zwei Arten bestimmt werden: Die Unsicherheit muss recherchiert werden oder sie kann mit statistischen Mitteln abgeschätzt werden. |
(B2) Addition relativer Unsicherheiten Verrechnung unsicherheitsbelasteter Größen mit Konstanten und Fortpflanzung von Unsicherheiten in physikalischen Gesetzmäßigkeiten (Punktrechnung) |
| (A3) Messabweichung
Definition und Nennung der Eigenschaften der Messabweichung |
(B3) Gauß'sche Unsicherheitsfortpflanzung* Weiterführende Rechnungen über mehrere Stufen, in denen unsicherheitsbehaftete Größen auftreten, allgemeiner Ansatz zur Unsicherheitsfortpflanzung |
| (C) Grafische Auswertung | (D) Signifikanz |
| (C1) Unsicherheitsflächen
Darstellung von Messwerten mit Unsicherheiten im Koordinatensystem. Einführung von Unsicherheitsbalken in x- und y-Richtung. |
(D1) Vergleich von Messergebnissen Unterscheidbarkeit wird als Überschneidung von Unsicherheitsintervallen eingeführt. Insbesondere über den grafischen Zugang und der dazugehörigen Überlappung der Intervalle wird die Verträglichkeit von Messergebnissen verdeutlicht. |
| (C2) Ausgleichsgeraden
Einführung der Grundlagen für die Regression. Schüler*innen lernen die Eigenschaften der Ausgleichsgerade kennen. |
Einführung von Boxplots als weitere Darstellung eines Messergebnisses. Untersuchung der Quartile als propädeutischer Aspekt für die Einführung der Signifikanz. |
| (C3) Drei-Geraden-Methode
Eine Ausgleichsgerade ist in den seltensten Fällen eindeutig. Eine sinnvolle Ausgleichsgerade kann über die Drei-Geraden-Methode ermittelt werden. |
(D3) Hypothesentests* Einführung des Signifikanzbegriffs. Bedeutung des Signifikanzniveaus sowie Fehler erster und zweiter Art. |
Vergleich von Datenreihen
Diese Unterrichtseinheit führt die Schülerinnen und Schüler in das Thema "Messunsicherheiten" ein und vermittelt, wie Messergebnisse richtig verglichen werden. Die Lernenden bearbeiten selbstständig fünf Schritte:
- Ursachen von Messunsicherheiten
- Relevanz und Bedeutung von Messunsicherheiten
- Berechnung und Bedeutung des Mittelwertes
- Berechnung und Bedeutung der Messunsicherheit
- Vergleich von Messergebnissen
Jeder Schritt beginnt mit einem Video (2 bis 4 Minuten), gefolgt von praktischen Übungsaufgaben. Bei einer falschen Antwort erhalten die Schülerinnen und Schüler helfende Hinweise in Rot, bei einer richtigen Antwort eine zusätzliche Erklärung in Grün.
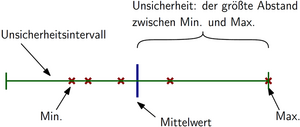
Um die Messunsicherheit zu quantifizieren, wurde die Maximalunsicherheit gewählt, also der maximale Abstand zwischen dem Mittelwert und einem der Messwerte (sehe Abbildung). Dies ist eine (große) Überschätzung der Messunsicherheit, aber mathematisch einfach. Auf diese Weise kann der Schwerpunkt auf die Bedeutung der Messunsicherheit und nicht auf die Berechnung gelegt werden. Diese Quantifizierung kann natürlich ein hervorragender Ausgangspunkt für eine Klassendiskussion und eine weitere Verfeinerung der Quantifizierung sein – vom Ausschluss von Ausreißern bis zur Berechnung der Standardabweichung.
Diese Unterrichtseinheit wurde in einer wissenschaftlichen Studie erfolgreich erprobt[1] und gibt den Lernenden alle Werkzeuge an die Hand, die sie benötigen, um zwei Messergebnisse korrekt zu vergleichen.
Diese Unterrichtseinheit ist geeignet für die Sekundarstufe I und II und hat eine Bearbeitungsdauer von etwa 60 Minnuten. Weitere Informationen zu dieser Lehreinheit finden Sie unserem Beitrag auf Lehrer-Online.
Eine englische Übersetzung der Unterrichtseinheit finden Sie hier.