Interferenz von Mikrowellen
| Interferenz von Mikrowellen | |
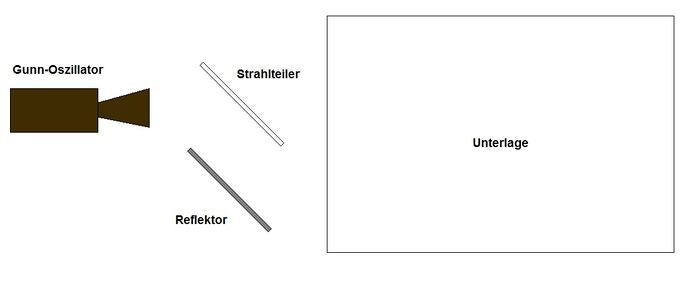
 Abb.1: Versuchsaufbau zur Mikrowelleninterferenz | |
| Kurzbeschreibung | |
|---|---|
| Qualitative Untersuchung des Interferenzmusters von Mikrowellen | |
| Kategorien | |
| Elektrizitätslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung, Energie |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Marco Damköhler |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Marc Müller |
Welleneigenschaften wie Reflexion, Beugung und Brechung sind Phänomene, die wir häufig im alltäglichen Leben wahrnehmen. Eine weitere wichtige Erscheinung ist die Überlagerung (Interferenz) von Wellen. Dabei kann jede Art von Welle interferieren, z.B. Schallwellen, Wasserwellen oder elektromagnetische Wellen, wozu u.a. die Lichtwellen, aber auch die Mikrowellen gehören. Der Frequenzbereich letzterer liegt etwa zwischen 3 und 10000 GHz, was einer Wellenlänge von ungefähr 10 cm bis 30 µm entspricht. [1]
Bei diesem Versuch experimentiert man mit Mikrowellen mit einer Frequenz von 9,4 GHz (Wellenlänge von 3,2 cm). Dabei soll das dabei entstehende Interferenzmuster untersucht werden.
Inhaltsverzeichnis
Didaktischer Teil
Mikrowellen sind heutzutage ein wesentlicher Bestandteil unseres Alltags. Fast jeder kennt den Mikrowellenherd aus dem Haushalt. Wenn man aber in der Physik von Mikrowellen spricht, so meint man die elektromagnetischen Wellen mit einer Frequenz von ca. 3 bis 10000 GHz. Dies ist einer wichtiger Aspekt, der den Schülerinnen und Schüler vorab verdeutlicht werden sollte. Weitere Geräte, die Wellen in diesem Frequenzbereich aussenden und vielen Kindern bekannt sind, sind z.B. WLAN-Router (2,4 - 2,48 GHz)[2], Bluetooth-Sender (2,40 - 2,48 GHz)[3] und Radaranlagen (30 MHz - 98 GHz)[4].
Zudem sollten bei diesem Versuch die Schülerinnen und Schüler bereits Vorkenntnisse über Wellen und deren Eigenschaften wie Reflexion, Beugung und Brechung haben. Es wäre auch sinnvoll bereits über die Interferenz gesprochen bzw. sogar mit Experimenten dieses Phänomen bei anderen "Wellenarten" (z.B. Schallwellen oder Wasserwellen) genauer beleuchtet zu haben. Darauf aufbauend kann dieses Experiment erfolgen, indem die Interferenz von Mikrowellen betrachtet wird. In der Schule behandelt man in der Sekundarstufe II allgemeiner die elektromagnetischen Schwingungen und Wellen.
Das Besondere an diesem Versuch ist, dass erstens die Interferenz von Mikrowellen nachgewiesen wird und zweitens das Interferenzmuster visualisiert wird. Dabei steht, neben der Tatsache, dass Mikrowellen interferieren, die Form des Musters im Vordergrund. Die Schülerinnen und Schüler sollten hier zu der Erkenntnis gelangen, dass es Extrema gibt und alle Maxima und Minima der selben Ordnung nicht auf einer Geraden liegen. Dieser Apsekt wird im Unterricht nämlich oft vernachlässigt, da bei sehr großer Entfernung zum Schirm, die bei der Interferenz entstehenden Kurven, als Geraden angenähert werden können. Den Schülerinnen und Schüler sollte hier aber verständlich gemacht werden, dass dies nur eine Approximation ist. Mit Hilfe der Theorie können diese Kurven noch genauer analysiert werden, sodass man letztendlich auf hyperbolische Funktionen stößt. Die Auswertung erfolgt auf rein qualitativer Ebene. Anschließend kann man die Interferenz des Lichts behandeln. Licht kann auch als elektromagnetische Welle ausgefasst werden, welches jedoch eine um vier bis sechs Größenordnungen kleinere Wellenlänge als die Mikrowellen hat.
In der Schule werden häufig Interferenzversuche mit Laserlicht gemacht, z.B. Doppelspaltversuch. Hier fällt jedoch oftmals die Dreidimensionalität dieses Phänomens unter den Tisch. Das durch den Spalt geschickte Licht wird auf einen Schirm projeziert. Betrachtet man den Schirm, so sieht man nur Punkte bzw. Streifen, die auf einer horizontalen Geraden liegen. Die Schülerinnen und Schüler könnten somit die räumliche Ausbreitung komplett unbeachtet lassen. Hier leistet der Mikrowellenversuch mehr, indem zumindest ein zweidimensionales Muster zum Vorschein kommt.
Des Weiteren wird hier (anders als bei der Wellenwanne oder bei der akustischen Interferenz mit Stimmgabeln) mit nur einem einzigen Sender und mit Hilfe eines Strahlteilers eine Überlagerung der Wellen erzeugt. Dies könnte weiter betrachtet bis zur Holografie führen.
Versuchsanleitung
Aufbau
Als Mikrowellensender wird ein Gunn-Oszillator verwendet. Dieser erzeugt elektromagnetische Wellen mit einer Frequenz von 9,4 GHz und einer Ausgangsleistung von 5 mW. Die Gleichspannung für den Oszillator liefert das Gunn-Versorgungsgerät. Am Gunn-Versorger wird zusätzlich eine E-Feld-Sonde und ein Spannungsmessgerät angeschlossen. Der im Versorger eingebaute Verstärker dient dazu, die Empfangssignale der Sonde auf ein leichter nachweisbares Niveau anzuheben. Der genaue Schaltplan zur Inbetriebnahme des Gunn-Oszillators und des Versorgungsgerätes ist der Leybold Gebrauchsanweisung 737 020, S.3, Fig.2[5] zu entnehmen.
Wichtig für die Interferenz ist die Tatsache, dass man mindestens zwei Wellen braucht, die sich dann zu einer Welle überlagern können.
Um sich erstmal mit den Geräten vertraut zu machen, bietet es sich an, zuerst eine stehende Welle zu erzeugen. Dazu stellt man in einiger Entfernung gegenüber des Gunn-Oszillator einen Reflektor auf. Dazwischen befindet sich die E-Feld-Sonde.
Da in diesem Versuch das Hauptaugenmerk auf der räumlichen Ausbreitung des Interferenzmusters liegt, braucht man hier jedoch mindestens zwei Quellen. Hierzu bietet es sich an, einen Strahlteiler zu verwenden. Dieser teilt die vom Sender eingehende Welle in zwei Teilwellen auf. Dafür eignet sich eine Platte aus Acrylglas, die in einem Winkel von 45° vor dem Sender platziert wird. Um die nun erhaltenen Teilwellen parallel auszurichten, benutzt man den Reflektor. Der gesamte Aufbau ist Abb.1 zu sehen. Der Anschaulichkeit halber folgt in Abb.2 der schematische Aufbau des Experiments.
Durchführung
Um die stehende Welle zu untersuchen, bewegt man die E-Feld-Sonde zwischen dem Reflextor und dem Gunn-Oszillator hin und her. Am Spannungsmessegerät ist erkennbar, dass sich Positionen mit minimaler Intensität und maximaler Intensität abwechseln.
Möchte man nun die räumliche Ausbreitung des Interferenzmusters analysieren, so braucht man als erstes eine große Unterlage. Auf dieser Unterlage werden möglichst parallele Linien eingezeichnet. Diese wird vor dem Mikrowellensender platziert und gut befestigt, damit sie nicht mehr verrutschen kann. Im Experiment wurden mehrere DIN-A4-Blätter mit Klebestreifen verbunden und anschließend damit auf dem Versuchstisch fixiert (vgl. Abb.4). Dann wird die E-Feld-Sonde entlang der Linien langsam bewegt. Mit dem Voltmeter kann man wiederum die Orte maximaler Intensität bestimmen. Diese Orte werden auf der Unterlage markiert.
Ergebnisse und Auswertung
Eine Überlagerung von Wellen kann natürlich auch zur destruktiven Interferenz führen. Das bedeutet, dass sich die Wellen gegenseitig auslöschen, wodruch die resultierende Welle verschwindet. An diesen Stellen würde man Minima erhalten. Der Abschnitt wird sich im Weiteren nur auf die Maxima beziehen, da auch nur diese im Experiment gemessen wurden.
Des Weiteren wird auch der Teil zur stehenden Welle nicht weiter erläutert, da dies nur zum Kennenlernen der Geräte dienen soll, aber keine nähere Relevanz für das räumliche Interferenzmuster hat.
Theoretische Vorbetrachtung
Wie schon erwähnt, ist die Interferenz ein dreidimensionales Phänomen. Für die Betrachtung des Versuches reicht es jedoch aus, dies auf zwei Dimensionen zu reduzieren. Dabei seien A und B zwei Sender, welche halbkreisförmige (im Dreidimensionalen halbkugelförmige) kohärente Wellen aussenden.
Dort, wo sich die Wellenfronten schneiden, also überlagern, erhält man Maxima. Die Ordnung der Maxima entspricht dabei der Differenz der Wellenfronten, z.B. ist das Maximum vom Schnitt des ersten roten Halbkreises mit dem des zweiten schwarzen Halbkreises ein Maximum der ersten Ordnung; genauso wie der Schnitt des dritten roten Halbkreises mit dem des vierten schwarzen Halbkreises usw. (vgl. Abb.3).
Verbindet man die Maxima der selben Ordnung, so erhält man Hyperbeln. Die Hyperbeln nähern sich asymptotisch Geraden an. Nach ungefähr fünf Perioden, kann man sagen, dass die Krümmung der Hyperbeln nur noch sehr gering ist und demzufolge eine Approximation als Geraden für große Entfernungen sinnvoll ist. Da in diesem Versuch die Mikrowellen eine Wellenlänge von ca. 3,2 cm haben, kann man diese Näherung bei einer Entfernung von etwa 16 cm zum Schirm anwenden. Bei Licht (Wellenlänge 600 nm) würde dies schon bei 3 µm der Fall sein.
Mit der Abb.3 soll nicht nur die Tatsache verdeutlicht werden, dass Interferenzhyperbeln entsehen, sondern auch das Verhalten von verändertem Senderabstand aufzeigen. Dabei sieht man, dass auch bei größer werdender Enfernung der Sender zueinander immer noch gekrümmte Kurven zu Stande kommen, wobei die Anzahl dieser zunimmt. Zudem werden die Abstände zwischen den einzelnen Hyperbeln kleiner.
Auswertung des Versuches
Bewegt man die E-Feld-Sonde langsam über die eingezeichneten Linien auf der Unterlage, so kann man auf dem Voltmeter deutliche Spannungsmaxima erkennen und kann damit auf eine Überlagerung (also Interferenz) der Mikrowellen schließen. Hat man die Sonde über die gesamte Unterlage gerückt, erhält man mehrere Maxima. Durch das Verbinden der Maxima der gleichen Ordnung werden Kurven ersichtlich, die in etwa so aussehen, wie in Abb.4 gezeigt.
Mit Hilfe der Theorie lassen sich die Kurven als Hyperbeln interpretieren. Ohne theoretisches Hintergrundwissen, lassen sich nur schwer Hyperbeln vermuten. Jedoch erkennt man deutlich, dass keine Geraden entstehen, was man ja bei der Untersuchung der Interferenz von Lichtwellen immer als Näherung annimmt.
Die Abb.4 zeigt zwar einen ungefähren hyperbolischen Verlauf der Kurven, jedoch müsste eine genauere Wiederholung des Versuches stattfinden um die Theorie noch besser experimentell zu bestätigen.
Sicherheitshinweise
Die Frequenz der Mikrowellen, welche von dem Gunn-Oszillator erzeugt werden, liegt weit überhalb der üblichen Mikrowellengeräte im Haushalt (ca. 2,5 GHz). Außerdem liegt die Ausgangsleistung der Mikrowellen im Versuch bei lediglich 5 mW. Damit ist ein gefahrloses Experimentieren möglich. Trotzdem sollte ein direktes Hineinschauen bei Betrieb vermieden werden.
Literatur
- ↑ Formeln und Tabellen für die Sekundarstufen I und II - 9.Auflage - Berlin - Verlag: Paetec
- ↑ Technische Daten zum WLAN Website des Schweizer Bundesamtes für Gesundheit. Abgerufen am 14. April 2013.
- ↑ Technische Daten zum Bluetooth Website des Schweizer Bundesamtes für Gesundheit. Abgerufen am 14. April 2013.
- ↑ Wellen- und Frequenzbereiche von Radargeräten radartutorial.de. Abgerufen am 14. April 2013.
- ↑ Gebrauchsanweisung für den Gunn-Versorger mit Verstärker (737 020) Leybold Didactic GmbH