Stehende Mikrowelle - Wellenlänge und Brechungsindex bestimmen
| Stehende Mikrowelle - Wellenlänge und Brechungsindex bestimmen | |
| Bestimmung der Wellenlänge einer Mikrowelle und der Brechzahl von einem Kunststoff | |
| Kurzbeschreibung | |
|---|---|
| Bestimmung der Wellenlänge einer stehenden Mikrowelle und der Brechzahl von einem Kunststoff über die Änderung der Phasengeschwindigkeit. Methodischer Vergleich zur Bestimmung der Brechzahl über Winkel der Wellennormale beim Durchgang durch einen mit Quarzsand gefüllten Halbzylinder. | |
| Kategorien | |
| Optik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. I: P6 9/10 und W10 9/10, Sek. II |
| Basiskonzept: | Wechselwirkung, Materie |
| Sonstiges | |
| Durchführungsform | Schülergruppenexperiment, Schülerdemoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Dirk Rathke |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Das Spektrum elektromagnetischer Wellen ist sehr breit, die Wellenlänge kann Werte über viele Größenordnungen annehmen (103 - 10-12 m). Die Mikrowellen nehmen darin nur einen kleinen Bereich ein, ihre Wellenlängen liegen im Zentimeterbereich, deshalb werden sie auch Zentimeterwellen genannt.
Die Wechselwirkung elektromagnetischer Wellen mit Materie hängt maßgeblich von ihrer Wellenlänge ab. Aber stellen sich deshalb auch wellenoptischen Phänomene in Abhängigkeit von der Wellenlänge anders dar?
Bekannte Experimente aus der Lichtwellenoptik werden mit Mikrowellen durchgeführt. Wie erwartet, werden die bekannten Gesetze der Wellenoptik, Reflexion und Brechung, bestätigt. Auf Grund der Wellenlänge von Mikrowellen, kann im Gegensatz zum Licht, eine interessante Methode zur Messung von Brechzahlen vorgestellt werden.
Die hier vorgestellten Versuche sollen anregen, neben dem sichtbaren Licht auch das gesamte elektromagnetische Spektrum in die Wellenoptik einzubeziehen und Besonderheiten auf Grund der Lage im elektromagnetischen Spektrum klar herauszustellen. Diese Betrachtung bietet die Möglichkeit, den "Blick auf das Experiment als Lernerfahrung" im fachdidaktischen Kontext zu hinterfragen.
Inhaltsverzeichnis
- 1 Didaktischer Teil
- 2 Versuchsanleitung
- 3 Versuch 1 – Reflexion und stehende Welle mit Messung der Wellenlänge
- 4 Versuch 2 – Transmission einer Stehenden Welle in Kunststoff mit Bestimmung der zugehörigen Brechzahl
- 5 Versuch 3 – Brechung am Halbzylinder mit Ermittlung der zugehörigen Brechzahl
- 6 Auswertung und Diskussion der Versuchsreihe
- 7 Literatur
- 8 Siehe auch
Didaktischer Teil
"Blick auf das Experiment als Lernerfahrung"
Das physikalische Experiment ist für den naturwissenschaftlichen Unterricht in zweifacher Hinsicht bedeutsam. Einmal als Erfahrung einer typischen Tätigkeit in den Naturwissenschaften und zum anderen als ein wichtiger Lernprozess für Schülerinnen und Schüler (SuS) im Unterricht. Häufig wird dieser Lernprozess aus der offensichtlichen Einsicht oder dem Erlebnis beim Experimentieren der SuS abgeleitet. Reinders Duit arbeitet in „Vorstellung und Experiment“ [1] klar heraus, dass die Vorstellungen der SuS auch ihre Beobachtungen leiten, ebenso „überzeugt viele Schüler die empirische Evidenz (von Experimenten) nicht ohne weiteres“. Es wird also etwas mehr notwendig sein, als ein "überzeugendes" Experiment. Selbst in der Geschichte der Naturwissenschaften finden sich Beispiele dafür, wie Erkenntnis durch Vorstellungen geleitet wurde - vergleiche geozentrisches Weltbild. Wie verhält sich damit der Zusammenhang zwischen Experiment und Verstehen in der Schule? Ist der Schluß vom Sehen, Hören usw. zum Verstehen einlösbar?
Die Unterrichtspraxis zeigt häufig, dass Lernerfolge der SuS beim Experimentieren hinter den Erwartungen zurückbleiben. Zwischen offenen und geschlossenen (nach Anleitung) Experimenten gibt es hinsichtlich der Lernerfolge keine signifikanten Unterschiede [2]. Weiter führt Scheid aus, dass es im wesentlichen auf multiple Repräsentationen und kognitive Aktivierungen der SuS ankommt, die für das Verständnis von physikalischen Vorgängen hilfreich sind. Das Konstruieren eines Konzeptes bedarf vieler Handlungen [3] und kann sicher nicht über singuläre Experimente erfolgen. Rogge empfiehlt die intuitive Erfassung einer Regelhaftigkeit bei Wiederholung bzw. ähnlichen Prozessen, Variationen, zusätzliche Strukturierungsmaßnahmen und Anwendungen des erstmalig entwickelten Konzeptes.
Was bedeutet das konkret für den Physikunterricht? Viele wellenoptische Phänomene werden in der Schule ausschließlich mit sichtbaren Licht dargestellt bzw. untersucht. Damit wird häufig das Modell elektromagnetische Welle nur über Licht etabliert. Aber das sichtbare Licht nimmt nur einen kleinen Bereich des elektromagnetischen Spektrums ein und besitzt zudem eine sehr kleine Wellenlänge. Mikrowellen haben dem gegenüber eine millionenfache größere Wellenlänge (einige Zentimeter), die mit einer E-Feldsonde leicht messbar ist. Der Unterschied der Wellenlänge von Licht und Mikrowellen bringt für das Experiment als Lernerfahrung interessante Vorteile. Sehr leicht kann z.B. die Frage untersucht werden: ob sich wellenoptische Phänomene in Abhängigkeit von der Wellenlänge anders darstellen? Allein durch die Variation der Wellenlänge kann das Modell elektromagnetische Welle im Unterricht auf Gültigkeit überprüft werden. Außerdem erlauben Mikrowellen Variationen der bekannten Standardexperimente in der Wellenoptik. Die Wellenlänge von Mikrowellen im Zentimeterbereich kann messtechnisch leicht erfasst werden und dadurch lassen sich stehende Mikrowellen recht einfach im Gegensatz zu Licht nachweisen. Selbst der Brechungsindex eines Materials kann mittels stehender Mikrowellen leicht ermittelt werden. So können SuS mit dem Modell elektromagnetische Welle Vorhersagen treffen und mit Experimenten überprüfen. Mikrowellen ermöglichen im Unterricht vielfältige Strukturierungsmöglichkeiten des Modells elektromagnetische Welle und gleichzeitig einfache Experimente als Lernerfahrung. Die hier vorgestellte Versuchsreihe bietet genau diese Aspekte.
Nach dem Rahmenlehrplan für Berlin und Brandenburg können die vorgestellten Experimente in folgende Module eingebunden werden:
- Sek. I, P6 9/10: "Von der Quelle zum Empfänger" (mehr Schwingung als Wellen), Akustik, longi./transv. Wellen,
- Sek. I, W10 9/10: "Natur des Lichts" - Themenfeld Optik, Wellentheorie,
- Sek.II: Elektromagnetische Wellen, von der Induktion.., Hertz'sche Wellen, Licht, Wellenoptik.
Versuchsanleitung
Insgesamt sind hier drei Experimente dokumentiert. Das erste Experiment zeigt die Reflexion von Mikrowellen an einer Metallplatte und die Ausbildung einer stehenden Welle. An der stehenden Welle kann die Wellenlänge der Mikrowelle gemessen werden. Das zweite Experiment zeigt durch das Hinzufügen einer Kunststoffplatte in das erste Experiment, dass Mikrowellen durch bestimmte opake Materialien transmittieren. Durch die Änderung der Phasengeschwindigkeit in der Kunststoffplatte kann auf die Brechzahl dieser geschlossen werden. Das dritte Experiment, vermutlich weniger überraschend, zeigt das Brechungsgesetz der Wellenoptik in einem klassischen Aufbau an einem Halbzylinder. Diese zweite Methode, Bestimmung der Brechzahl über Ein- und Ausfallwinkel, dient als Referenzmessung. Für die Experimente werden folgende Geräte und Zubehör benötigt:
- Generator und Verstärker (Gunn-Versorgung und Meßverstärker), Geräte Nr. 737 020 der LD DIDACTIC GmbH,
- Mikrowellenquelle (Gun-Element) mit Hornantenne, Geräte Nr. 737 01 und 737 21 der LD DIDACTIC GmbH,
- E-Feld-Sonde, Geräte Nr. 737 35 der LD DIDACTIC GmbH,
- Metall- und PE/PVC-Platte, Geräte Nr. 737 27 der LD DIDACTIC GmbH (Zubehör Physik Mikrowellen I)
- Halbzylinder hohl mit Quarzsand, Geräte Nr. 737 275 der LD DIDACTIC GmbH (Zubehör Physik Mikrowellen II)
- Voltmeter, Meßbereich ca. 3V
- langes Lineal min. 30 cm mit Millimetereinteilung
- Winkelmesser groß
- Stativmaterial
- 2 x 2m Koaxial-/HF-Kabel und diverse Bananenstecker-Kabel
Eine elektromagnetische Welle besteht aus einer E- und B-Feldkompnente die senkrecht zueinander und senkrecht zur Propagationsrichtung stehen. E- und B-Feld sind über den Wellenvektor und die Lichtgeschwindigkeit gekoppelt, ihre Amplituden sind proportional zueinander.
In den folgenden Experimenten wird nur die E-Feldkomponente gemessen. Entsprechend könnte mit einer B-Feld-Sonde auch das B-Feld berücksichtigt werden, womit aber analoge Ergebnisse zu erwarten sind.
Die E-Feld-Sonde misst die E-Feld-Komponente der Mikrowelle parallel zur Längsachse der Stabsonde (die Ausrichtung kann mittels Polarisationsgitter nachgewiesen werden). Die E-Feldmessung erfolgt nahezu punktuell, eine Hochfrequenzdiode richtet das Signal gleich. Die Diodenkennlinie ist nicht linear und die verwendete Mikrowellenquelle besitzt eine spezifische Abstrahlcharakteristik, aber trotzdem verhält sich die gemessene Spannung in guter Näherung proportional zum Quadrat der E-Feldkomponente.
Versuch 1 – Reflexion und stehende Welle mit Messung der Wellenlänge
Im ersten Versuch wird mittels E-Feld-Sonde eine stehende Welle zwischen Gunn-Oszillator mit Hornantenne (Mikrowellenquelle) und Metallplatte nachgewiesen. Eine stehende Welle zeichnet sich durch Knoten (keine Intensität) und Berge (maximale Intensität) in periodischer Wiederholung aus. Über die Knotenabstände der stehenden Welle kann deren Wellenlänge über die Beziehung Wellenlänge λ = doppelter Knotenabstand ermittelt werden. Der vorgestellte Versuch orientiert sich an LB Handblätter Physik, Versuch P3.7.4.2 (siehe [1] LB P3.7.4.2).
Aufbau
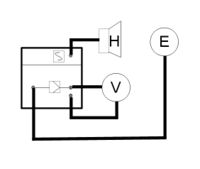
Zum Versuchsaufbau siehe Bild 1. Zwischen Gunn-Oszillator mit Hornantenne (B) und einer Metallplatte (D) mit ca. 40 cm Abstand wird ungefähr mittig die E-Feld-Sonde (C) mit Ausrichtung des Kopfes zur Metallplatte (D) positioniert. Die Hornantenne, der Kopf der E-Feld-Sonde und die Mitte der Metallplatte sollten sich auf einer gemeinsame Höhe befinden, ggf. an den Stativen einstellen. Die elektrischen Signalanschlüsse (a), (b) und (c) des Spannungsmesser (A), des Gunn-Oszillators (B) und der E-Feld-Sonde (C) am Generator/Messverstärker (737 020 LD Didactic) erfolgen nach dem Schaltungsschema in Bild 2 (Voltmeter V, Gunnelement H und E-Feldsonde E). In der Schaltung sind unbedingt HF-Kabel anzuwenden, ausser für den Spannungsmesser. Am Spannungsmesser wird ein Messbereich von 0 - 3 V (DC) eingestellt, ein optimaler Zeigerausschlag (Signalstärke) zwischen Signalminimum und -maximum durch Verschieben der E-Feld-Sonde (C) überprüft und gegebenfalls muss der Messbereich oder die Abstände von Sonde und Metallplatte angepasst werden. Es ist darauf zu achten, dass sich keine Stöhrquellen oder Reflektoren in der Versuchsumgebung befinden. Unter der E-Feld-Sonde kann ein Blatt Papier liegen, um darauf im Verlauf des Experiments die Sondenposition zu markieren.
Durchführung
Nach der Prüfung und Justierung des Aufbaus wird langsam die E-Feld-Sonde auf die Metallplatte zubewegt bis das Voltmeter einen minimalen Ausschlag zeigt. An dieser Stelle befindet sich ein Wellenknoten und es wird die Position der E-Feld-Sonde markiert. Nun wird die E-Feld-Sonde weiter verschoben und es werden die nächsten Orte der Wellenknoten markiert. Die Sonde kann ggf. auch von der Metallplatte entfernt werden. In der dokumentierten Messreihe wurden 9 aufeinanderfolgende Knotenpositionen markiert und der jeweilige Abstand mit einem Lineal (mit Millimetereinteilung) gemessen.
Ergebnisse und Zwischenauswertung
Die gemessenen Knotenabstände z sind in folgender Tabelle eingetragen:
| Messung | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| z in cm | 1,6 | 1,5 | 1,6 | 2,1 | 1,2 | 1,4 | 1,8 | 1,4 | 1,9 |
Die Wellenlänge λ berechnet sich aus dem Knotenabstand z wie folgt λ = 2z.
Für den mittleren Knotenabstand erhalten wir aus den Messdaten 1,6 cm und als mittlere Abweichung 0,2 cm. Daraus folgt mit dem mittleren Knotenabstand ẑ = (1,6 ± 0,2) cm die Wellenlänge λ = (3,2 ± 0,4)cm. Weitere Messunsicherheiten ergeben sich aus der Längenmessung der Knoten und kann mit ± 0,1 cm angenommen werden. Der Referenzwert vom Hersteller beträgt λR = 3,3 cm und liegt damit innerhalb der Messunsicherheit.
Versuch 2 – Transmission einer Stehenden Welle in Kunststoff mit Bestimmung der zugehörigen Brechzahl
Für den zweiten Versuch wird der Aufbau für die stehende Mikrowelle aus Versuch 1 übernommen, um den Brechungsindex einer Kunststoffplatte zu bestimmen. Dazu wird die Änderung der Ausbreitungsgeschwindigkeit der Mikrowelle innerhalb der Kunsstoffplatte genutzt. Damit verschiebt sich die Position der Knoten der stehenden Welle außerhalb der Platte. Mittels Verschiebung der Metallplatte kann die Knotenposition mit der Ursprungslage in Übereinstimmung gebracht werden. Aus der Verschiebung der Metallplatte Δz und der Dicke d der Kunststoffplatte kann auf den Brechungsindex der Kunststoffplatte nach folgender Beziehung geschlossen werden:
d/λn = (d + Δz)/λ da nLuft = 1 folgt
n = λ/λn = 1 + Δz/d
Aufbau
Der Aufbau von von Versuch 1 wird durch eine Kunststoffplatte (D) mit 2 cm Dicke ergänzt, wie in Abbildung 3 dargestellt.
- PE/PVC-Platte, Geräte Nr. 737 27 der LD DIDACTIC GmbH (Zubehör Physik Mikrowellen I)
Durchführung
Nach dem Aufstellen der PVC-Platte, siehe Bild 3, ist die E-Feld-Sonde so in Längstrichtung zwischen Platte und Gunn-Oszilator zu verschieben, dass das Voltmeter ein Maximum der Feldstärke anzeigt. Nun wird die Metallplatte langsam in Richtung Kunststoffplatte verschoben, bis ein Minimum angezeigt wird. Diese Position wird markiert. Das Verschieben wird bis zum nächsten Minimum fortgesetzt und der Längenabstand mit einem Lineal gemessen. So sollten mehrmals zwei Minima gefunden und die jeweilige Längendifferenz der Positionen der Metallplatte erfasst werden.
Ergebnisse und Zwischenauswertung
Die gemessenen Verschiebungen Δz sind in folgender Tabelle eingetragen:
| Messung | 1 | 2 | 3 | 4 | 5 |
| Δz in cm | 1,6 | 1,7 | 1,6 | 1,6 | 1,7 |
aus den Messwerten erhalten wir eine durchschnittliche Längendifferenz von Δẑ = (1,6 ± 0,04) cm.
Aus der Dicke d = 2 cm der Kunststoffplatte erhalten wir über folgende Beziehung ihren Brechungsindex:
d/λn = (d + Δẑ)/λ mit nLuft = 1 folgt
n = λ/λn = 1 + Δẑ/d
Damit ergibt sich nKunststoff = 1,8 ± 0,02
Für die Kunststoffplatte gibt es leider keine Referenzwert durch den Hersteller. Der recherchierte Referenzwert für Kunststoff liegt um nR = 1,65
Versuch 3 – Brechung am Halbzylinder mit Ermittlung der zugehörigen Brechzahl
Im dritten Experiment wird der Brechungsindex von Quarzsand über die Brechung einer Mikrowelle an einem Halbzylinder gefüllt mit Quarzsand bestimmt. Der Brechungsindex n wird hier nicht über die Wellenlänge nach n = λ/λn bestimmt, sondern über den Einfallwinkel α und Ausfallwinkel β von Quarzsand nach Luft (von optisch dicht zu dünn) mittels Snelliussches Brechungsgesetzes n = sinα/sinβ. Der vorgestellte Versuch orientiert sich an LB Handblätter Physik, Versuch P3.7.4.5 (siehe [2] LB P3.7.4.5).
Aufbau
Der Aufbau des Experiments erfolgt gemäß Bild 4. Die Hornantenne B sitz möglichst dicht an der runden Seite des mit Quarzsand gefüllten Halbzylinders C, sodass der Einfallswinkel α mit dem Einfallslot zusammen fällt. Die E-Feld-Sonde D steht auf der anderen Seite des Halbzylinders, um das Maximum des Ausfallstrahls zu finden. Auf eine gleiche Höhe von Antenne, Halbzylinder und Sonde ist zu achten. Die E-Feldkomponente wird wieder mit einem Voltmeter A gemessen, zur Versorgung und Signalverstärkung wird die bereits vorhandene Schaltung nach Bild 2 genutzt.
Durchführung
Der Halbzylinder ist mit einem Einfallswinkel von 0° zur Hornantenne ausgerichtet, d.h. die angenommene Wellennormale steht senkrecht auf der gegenüberliegenden Seite, dem Durchmesser des Halbzylinders. Schrittweise wird nun der Halbzylinder gedreht, erst in die eine Richtung und anschließend in die andere, sodass Einfallswinkel von 20° bis 40° in 5°-Schritten durchlaufen werden. An jeder Position wird mit der E-Feldsonde der Ausfallwinkel der ausfallenden Mikrowelle gemessen. Hier sollte auf eine deutliche Signalstärke geachtet werden. Die Werte für den Einfall- und Ausfallwinkel sind in einer Tabelle zu erfassen.
Ergebnisse und Zwischenauswertung
Die Messwerte für die Ein- und Ausfallwinkel sind in folgender Tabelle aufgelistet:
| α in ° | 40 | 35 | 30 | 25 | 20 | -20 | -25 | -30 | -35 | -40 |
| β in ° | 23 | 20 | 19 | 15 | 13 | -13 | -16 | -18 | -20 | -23 |
Die einfallende Mikrowelle fällt senkrecht auf die gewölbte Halbzylinderseite, deshalb kann (leicht idealisiert) über die gemessenen Winkel direkt auf die Brechung von Quarzsant nach Luft geschlossen werden. Der Brechungsindex für die Zylinderwand wird vernachlässigt und für Luft mit nLuft=1 angenommen.
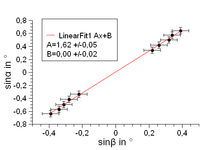
Die Sinuswerte der gemessenen Winkel wurden im Diagramm, siehe Bild 5, aufgetragen als sinα = f(sinβ) und mit der Funktion sinα = A*sinβ + B gefittet.
Aus dem Anstieg A kann direkt der Brechungsindex nQuarz (= sinα/sinβ) = 1,62 ± 0,05 für Quarzsand abgelesen werden. Der Referenzwert beträgt nR = 1,66 (1,74 nach LB Arbeitsblatt).
Auswertung und Diskussion der Versuchsreihe
Die Versuchsreihe hat gezeigt, dass bekannte Versuche aus der Lichtoptik, wie Reflexion und Brechung, auch mit Mikrowellen funktionieren und die Reflexions- und Brechungsgesetze der Licht-/Wellenoptik bestätigen. In der Transmission gibt es Unterschiede, manche für Licht opake Stoffe, wie die im Experiment 2 genutzte graue Kunststoffplatte bzw. der Quarzsand im Experiment 3, sind für Mikrowellen transparent. Wegen der wesentlich größeren Wellenlänge der Mikrowellen gegenüber Licht, kann die Wellenlänge direkt aus einer stehenden Welle gemessen werden. Deshalb kann mit einfachen Versuchsaufbauten der Brechungsindex nach dem Snelliusschen Brechungsgesetz sowohl über die Verschiebung der Wellenlänge (Experiment 2), somit über die Phasengeschwindigkeit, als auch über die Ein- und Ausfallswinkel (Experiment 3) ermittelt werden.
Die Abweichung der ermittelten Brechzahl für Kunststoff im Experiment 2 zum Referenzwert liegt zum einen am unsicheren Referenzwert und zum anderen wird vorausgesetzt, dass die Wellenausbreitung innerhlab der Platte wie eine ebene Welle erfolgt. Zum besseren Methodenvergleich der Bestimmung der Brechzahl in Experiment 2 und 3 sollte der gleiche Stoff/Festkörper genutzt werden. Die Ergebnisse liegen sonst mit den Unsicherheiten nahe den jeweiligen Referenzwerten, wobei die Genauigkeiten der Referenzwerte für die Kunststoffplatte und den Quarzsand leider unbekannt sind.
Mit den vorgestellten Experimenten konnte nachgewiesen werden, dass die Wellenlänge einer stehenden Mikrowelle im Unterricht leicht und hinreichend genau messbar ist. Der Brechungsindex eines Materials kann mittels stehender Welle leicht, aber nur in der Größenordnung, ermittelt werden. Die SuS können im Unterricht Vorhersagen aus dem Modell elektromagnetische Welle treffen und experimentell überprüfen. Die Experimente sind als Variation der Standardexperimente in der Wellenoptik sehr gut für Lernerfahrungen geeignet.
Sicherheitshinweise
Da Mikrowellen mit Kohlenwasserstoffverbindungen wechselwirken, sind beim Experimentieren grundsätzlich entsprechende Sicherheitsbestimmungen einzuhalten. Für energiereiche Mikrowellen gilt besonders: großen Abstand zur Quelle einhalten, um die Strahlungsenergie gering zu halten, die Ausbreitungsrichtung (Strahlungskeule) nicht auf Personen richten.
Die in den oben beschriebenen Experimenten genutzte Strahlungsquelle ist laut Herstellerangaben mit einer Leistung von 10 mW unbedenklich.
Literatur
- ↑ Duit, Reinders; Schülervorstellungen, R. Müller et.al, Aulis Verlag 2011
- ↑ Scheid, Jochen; Multiple Repräsentationen,Verständnis physikalischer Experimente und kognitive Aktivierung, Logos, Berlin, 2013
- ↑ Rogge, Christian; Entwicklung physikalischer Konzepte in aufgabenbasierten Lernumgebungen, Logos, 2010
- LB P3.7.4.2: LB Handblätter Physik, Versuch P3.7.4.2; http://www.ld-didactic.de/literatur/hb/d/p3/p3742_d.pdf [04.01.2015]
- LB P3.7.4.5: LB Handblätter Physik, Versuch P3.7.4.5; http://www.ld-didactic.de/literatur/hb/d/p3/p3745_d.pdf [04.01.2015]
- Versuche Mikrowellen: Versuchsbeschreibung Uni Duisburg; https://www.uni-due.de/physik/ap/ANLEITUNGEN/D16.pdf [04.01.2015]