Mechanische Schwingungen auf der Luftkissenbahn
| Mechanische Schwingungen auf der Luftkissenbahn | |
 Gleiter als Schwinger zwischen zwei Federn auf der Luftkissenbahn | |
| Kurzbeschreibung | |
|---|---|
| Die Luftkissenbahn bietet die Möglichkeit reibungsarme Federschwinungen in der Horizontalen einzuführen und quantitativ zu betrachten. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | ggf. Klasse 10, Sek II |
| Basiskonzept: | Energie |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Chris Patricia Hänsel |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Franz Boczianowski |
Schwingungen sind zeitlich periodische Vorgänge, bei denen verschiedene Energieformen periodisch umgewandelt werden. Bei mechanischen Schwingungen handelt es sich hierbei um die Umwandlung von potentieller in kinetische Energie und umgekehrt. Auf der Luftkissenbahn können wir einen horizontalen Federschwinger beobachten und die Auslenkung des Schwingers in Abhängigkeit von der Zeit messen. Auch die mathematische Betrachtung mechanischer Schwingungen bietet sich hier an.
Inhaltsverzeichnis
Didaktischer Teil
Schwingungen begegnen uns täglich in unserem Alltag, angefangen bei der Sirene des Krankenwagens, der an uns vorbeifährt, über die alte Uhr des Großvaters bis zur Schwingung unserer Herzmuskulatur. Schwingungen sind etwas selbstverständliches in unserem Leben, doch ohne sie gäbe es keine Sprache und keine Musik. Unsere Schüler*innen bringen jede Menge Vorwissen zum Thema Schwingungslehre mit, ein*e jede*r von ihnen weiß ganz genau, wie er*sie eine Schaukel auf dem Spielplatz antreibt, um dem Himmel ein Stück näher zu kommen. Und doch fällt ihnen die Beschreibung von Schwingungen mit Amplitude, Frequenz, Schwingungsdauer und Phasenwinkel zu Beginn häufig schwer.
Mit dem vorliegenden Experiment lässt sich die Auslenkung des Gleiters in Abhängigkeit von der Zeit beobachten und einfach in Diagrammen darstellen. Anhand des Versuchsaufbaus und der Diagramme kann man anschließend gut über die Eigenschaften von Schwingungen sprechen und zusätzlich auf die mathematische Beschreibung von Schwingungen eingehen. Obwohl eine gedämpfte Schwingung beobachtet wird, bietet es sich an, an dieser Stelle mathematisch zunächst über harmonische Schwingungen zu sprechen, indem eine Ausgleichsfunktion in das Diagramm gelegt wird. Die Funktion entspricht einer Sinusfunktion der Form
welche Schüler*innen der 10. Klasse in Mathematik schon kennengelernt haben und identifizieren können. In Sekundarstufe II haben die Schüler*innen zusätzlich die Differential- und Integralrechnung kennengelernt, wodurch auch die gemeinsame Lösung der Differentialgleichung
möglich wird. Hierbei ist zu beachten, dass die kumulierte Federkonstante beschrieben durch die Summe der Federkonstanten beider Federn ist. Die hierfür benötigte Ableitung von Winkelfunktionen wird seit der Umstellung auf das G8-Abitur zumeist nicht mehr behandelt, ist aber leicht einzuführen. In meinen Augen ist es nicht sinnvoll auch den Umgang mit Anfangsbedingungen einzuführen, sondern nur die Berechnung bis zur allgemeinen Lösung
durchzuführen.
Versuchsanleitung
Aufbau
Nachfolgend werden die Materialien und Geräte beschrieben, welche für den Versuch benötigt werden. Da es mehrere Möglichkeiten gibt die Messung aufzunehmen habe ich die Materialien für den mechanischen Grundaufbau und die Messung getrennt erfasst. Im Anschluss an die Beschreibung des Versuchsaufbaus werden die Vor- und Nachteile der einzelnen Messmethoden kurz beschrieben.
Für die Luftkissenbahn:
- Luftkissenbahn mit zugehörigen Endstoppern (z.B. PHYWE Artikel-Nr.: 11202-17)
- Gebläse und Schlauch zur Luftkissenbahn
- 1 Luftkissenbahnschlitten
- 4 Haken zum Einstecken
- 2 Federn mit gleicher Federkonstante
- Wasserwaage
Für die Messung:
- Messung mit CASSY
- CASSY-Grundmodul (Art. Nr. 524 013) inkl. USB-Kabel
- Bewegungsmesswandler (Art. Nr. 524 032) inkl. CASSY-BMW-Box und Anschlusskabel
- Stativmaterial (Fuß bzw. Tischklemme, 2 kurze Stativstangen, 2 Doppelmuffen)
- PC mit CASSY-Lab
- Angelsehne
- 1 weiterer Haken für den Gleiter der Luftkissenbahn
- 1 kleines Massestück (5 oder 10 g)
- Messung durch Videoanalyse
- Kamera mit Videofunktion
- Stativ zur Kamera bzw. geeignete Methode sie aufzustellen
- PC mit VianaNET oder anderer Videoanalyse-Software
Für den Grundaufbau der Luftkissenbahn wird zunächst geprüft, ob beide Endstopper an der Bahn befestigt sind und diese wenn nötig mit je zwei Schrauben befestigt. Die Bahn wird nun auf einen Versuchstisch gestellt und mithilfe der Stellschrauben unter der Bahn sowie einer Wasserwaage so ausgerichtet, dass sie sowohl der Breite, als auch der Länge nach gerade steht. Insbesondere letzteres ist wichtig, da sonst die Messungen verfälscht werden könnten. Im Anschluss wird das Gebläse mit dem zugehörigen Schlauch an der Bahn befestigt und je ein Haken in beide Endstopper gesteckt. Zu guter Letzt werden zwei Haken in den äußeren Steckplätzen des Gleiters befestigt und selbiger mithilfe der beiden Federn mit den Endstoppern verbunden und mittig auf der Bahn positioniert. Es bietet sich an die Federkonstante der beiden Federn zuvor zu bestimmen, um sie für die Berechnungen zur Verfügung zu haben.
Für die Messung mit CASSY Lab wird der Bewegungsmesswandler mit von Stativmaterial an einem Ende der Luftkissenbahn am Tisch befestigt bzw. aufgestellt. Die Angelsehne wird etwa in Länge der Luftkissenbahn zugeschnitten und an beiden Enden mit Schlaufen versehen, von denen eine an einem Haken auf dem mittleren Steckplatz des Luftkissenbahngleiters befestigt wird. Das andere Ende der Sehne wird über die Rolle des Bewegungsmesswandlers geführt und in die Schlaufe ein kleines Massestück eingehängt. Der Bewegungsmesswandler sollte hierfür geradlinig hinter der Bahn stehen, damit sich die Angelsehne nicht verfangen kann. Der Bewegungsmesswandler wird nun mithilfe der BMW-Box an das CASSY angeschlossen und selbiges mit dem PC verbunden.
Für die Messung mit Videoanalyse wird auf dem mittleren Steckplatz des Luftkissenbahngleiters ein Plättchen befestigt, welches in der Analyse als zu beobachtender Punkt dient. Die Kamera wird auf ein Stativ geschraubt bzw. anderweitig aufgestellt. Sie wird nun so eingestellt, dass die vollständige Schwingung aufgenommen werden kann. Hierfür ist es nicht notwendig die komplette Luftkissenbahn aufzunehmen.
Durchführung
In der Durchführung werden die Handhabung des Aufbaus und das Verfahren der Aufnahme von Messwerten bzw. der Beobachtung dargestellt. Um den Versuch zu beginnen muss zunächst das Gebläse eingeschaltet werden und die Stärke des Luftstroms so eingestellt werden, dass der Gleiter gut auf der Bahn schwingt, ohne plötzlich zu stoppen, da der Luftstrom nicht ausreicht. Hierbei ist zu beachten, dass der Luftstrom stärker sein muss, je schwerer der Gleiter ist. Beschwert man also den Gleiter mit Massestücken, welche im Material für die Luftkissenbahn vorhanden sind, so erfordert dies auch einen stärkeren Luftstrom, damit der Gleiter schwingt. Ist der Luftstrom eingestellt, so wird der Gleiter aus der Ruhelage ausgelenkt und somit in Schwingung versetzt. Nachfolgend werden die zwei Verfahren zur Messung näher beschrieben.
Messung mithilfe von Cassy und Bewegungsmesswandler
Bevor man die Messung mit CassyLab beginnt, ist die Aufnahme des Bewegungsmesswandlers zu eichen. In diesem wird der Weg, welchen der Gleiter zurücklegt gemessen, indem die Angelsehne eine Rolle im Gerät dreht. Während des Aufbaus bewegt man die Sehne auf der Rolle, wodurch das Cassy in der Ruhelage des Gleiters üblicherweise keine 0,00 cm anzeigt. Um den Bewegungsmesswandler zu eichen, tippt man in CassyLab die Schaltfläche -> 0 <-. Weiterhin bietet es sich an, den Messbereich im Diagramm einzugrenzen, da man den Gleiter im Allgemeinen nicht weiter als 20 cm auslenkt. Für die Messung wird der Gleiter aus der Ruhelage ausgelenkt, die Messung in CassyLab gestartet und nach etwa 10-15 vollen Schwingungen wieder gestoppt.
Messung mithilfe von Videoanalyse
Für die Aufnahme des Videos wurde hier eine Kompaktkamera (Nikon Coolpix L830, Videoeinstellung: 1080/25p) genutzt, welche wie oben beschrieben auf einen Stativ fixiert auf die Versuchsanordnung gerichtet wurde. Die Kamera wird hierbei mittig möglichst einige Meter von der Luftkissenbahn entfernt aufgestellt, um perspektivische Verzerrungen durch die Linse der Kamera so gering wie möglich zu halten. Vor Beginn der Aufnahme wird der aufgenommene Bereich durch geeignete Einstellungen des Zooms soweit verringert, dass die vollständige Schwingung aufgenommen wird, jedoch nicht der Rest der Luftkissenbahn. Weiterhin wird die Kamera auf den Gleiter fixiert, was insbesondere bei Kameras mit Autofokus notwendig ist, damit das Video nicht verschwommen ist. Sind diese Voreinstellungen getroffen, wird der Gleiter ausgelenkt und die Videoaufnahme gestartet. Die Aufnahme kann nach 10-15 vollen Schwingungen wieder gestoppt werden.
Um das Video in VianaNET zu analysieren muss es dort zunächst geladen und anschließend eingemessen werden. Hierfür wird eine bekannte Streckenlänge im Video markiert und ausgezeichnet. Anschließend wird ein Koordinatensystem angelegt, an welchem sich die Analyse orientiert. Für die Analyse selbst bietet es sich an die automatische Analyse des Programmes zu verwenden. Hierfür wählt man einen Punkt des Objektes aus, der eine Farbe besitzt die sich von den anderen Farben des Bildes gut abhebt, welche das Programm im Video verfolgen kann. Anschließend startet man die automatische Analyse.
Ergebnisse und Auswertung
Für die beiden für den Versuch verwandten Federn ergaben sich durch Messung die Federkonstanten
Damit ergibt sich insgesamt eine Federkonstante von
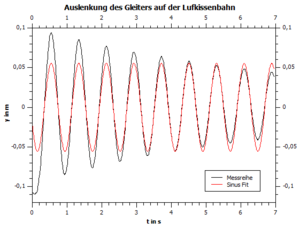
Betrachtet man die Ergebnisse der Messungen mithilfe des Bewegungsmesswandlers und des CASSY, so erkennt man im Diagramm die Darstellung einer schwach gedämpften Schwingung mit einer maximalen Auslenkung von 10 cm. Der softwareinterne Fit von QTI-Plot errechnet bei einem Ansatz von eine Ausgleichfunktion mit den Parametern
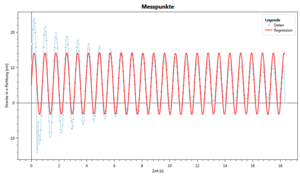
In der Videoanalyse ergab sich das nebenstehende Diagramm. In diesem erkennt man ebenfalls die Darstellung einer schwach gedämpften Schwingung, hier mit einer maximalen Auslenkung von etwa 8 cm. Zu beachten ist, das die Darstellung hier durch Viana in cm ausgegeben wurde statt wie oben in m. Hierdurch ergeben sich unterschiedliche Werte in der Ausgleichfunktion. Bei einem gewählten Ansatz von errechnet Viana die Parameter
Der Parameter dient hierbei der vertikalen Verschiebung der Funktion entlang der Auslenkungsachse und wird benötigt, da es in der Videoanalyse nicht einfach ist, das Koordinatensystem so einzulegen, dass die Schwingung um die Ruhelage bei gemessen wird. Um die Parameter mit den obigen vergleichen zu können, ist ausschließlich der Parameter umzurechnen, so dass sich ergäbe.
Betrachtet man diese Ergebnisse genauer und setzt sie in den Zusammenhang zu den Eigenschaften von Schwingungen, so lässt sich aussagen, dass die Schwingungen entsprechend der Ausgleichfunktionen eine Amplitude von 5,4 cm bzw 8,8 cm hatten, eine Schwingungsdauer von rund 0,79 s und eine Frequenz von rund 1,27 Hz. Man erkennt hier gut, dass Schwingungsdauer und Frequenz nicht von der Auslenkung abhängen sondern ausschließlich von Federkonstante und Masse des Körpers. Von diesen variiert ausschließlich die Masse marginal, da auf dem Gleiter das Plättchen für die Videoanalyse hinzukommt. Gleichzeitig entsteht jedoch weniger Reibung durch die hierbei fehlende Rolle des Bewegungsmesswandlers. Die Federkonstante hingegen bleibt gleich, da die Federn zwischen den versuchen nicht gewechselt werden.
Siehe auch
Mit dem Federpendel befassen sich auch der Artikel von Elisa Kagelmaker und der Artikel von Marcel Kerber zur Resonanz eines Federpendels. Elisa Kagelmakers Artikel legt hierbei ein besonderes Augenmerk auf die Bestimmung der Federkonstanten. Das Thema Mechanische Schwingungen findet man auch im Artikel Fadenpendel und Freier Fall von Robby Büchner sowie im Artikel Analogie zwischen Schwingungen und Kreisbewegungen von Pascal Scheipers.
Die Verwendung von Viana hat Josef Kaliski sehr ansprechend nochmals in seinem Artikel Messung der Erdbeschleunigung g (digital) mittels Video-/ Tonanalyse bzw. Lichtschranke beschrieben.