Analogie zwischen Schwingungen und Kreisbewegungen
| Analogie zwischen Schwingungen und Kreisbewegungen | |
| Abb. 1: Aufbau des Experiments | |
| Kurzbeschreibung | |
|---|---|
| Mit Hilfe dieses Versuches wird die Analogie zwischen einer harmonischen Schwingung und einer Kreisbewegung verdeutlicht. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | System |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Pascal Scheipers |
| Kontakt: | @ |
| Uni: | Ruhr-Universität Bochum |
| Betreuer*in: | R.Wackermann |
In diesem Versuch werden harmonische Schwingungen betrachtet und die mathematische Gleichbehandlung von Schwingungen und Kreisbewegungen verdeutlicht.
Inhaltsverzeichnis
Didaktischer Teil
In der Physik und somit auch im Physikunterricht werden häufig Analogien und Modelle als Vereinfachung komplexer Systeme bzw. zum formalen Beschreiben physikalischer Phänomene eingesetzt. In diesem Versuch werden Schwingungen betrachtet. Diese sind zwar anschaulich einfach zu erfassen, allerdings fällt es Schülerinnen und Schülern möglicherweise schwer, diese mathematisch zu beschreiben.
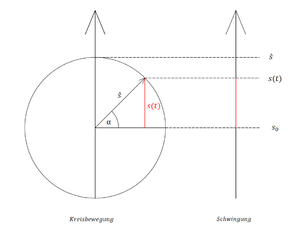
Um einen gut erfassbaren Einstieg zu schaffen, wird in diesem Versuch die Analogie zwischen harmonischen Schwingungen und Kreisbewegungen aufgezeigt. Wenn im Mathematikunterricht Kreisfunktionen behandelt wurden, können die Schülerinnen und Schüler an diesem Wissen anknüpfen. Mit Hilfe von Abbildung 2 erkennen die Schülerinnen und Schüler die zeitliche Abhängigkeit der Auslenkung und konstruieren so selbständig die Formel für die harmonische Schwingung.
Benötigte Vorkenntnisse
Da sich dieser Versuch als Einstieg in das Thema Schwingungen anbietet, sind keine Vorkenntnisse nötig. Es bietet sich an, das Thema Kräfte und Kräftegleichgewicht behandelt zu haben, um so den physikalischen Prozess der harmonischen Schwingung erklären zu können. Im Bereich der Mathematik werden die Kreisfunktionen vorausgesetzt.
Versuchsanleitung
Aufbau
Für den Aufbau des Experimentes wird zunächst ein Federpendel an eine Stativkonstruktion (vgl. Abb. 1) angebracht. Hierbei ist es empfehlenswert, eine Nut rund um den querlaufenden Stab zu fräsen, um ein etwaiges Verrutschen der Feder zu vermeiden.
Neben diesem Stativ wird ein weiteres aufgebaut, an welches ein regelbarer Motor angebracht wird. In dem Bohrfutter des Motors wird ein Stab eingebracht, an dem wiederum ein dünner Stab rechtwinklig fixiert ist. Am Ende dieses Stabes befindet sich eine Styropor-Kugel. Diese sollte etwa den gleichen Durchmesser wie die Kugel des Federpendels besitzen.
Dieser Aufbau wird nun von der Seite mit einer Projektionslampe (z.B. einer Kohlebogenlampe) so beleuchtet, dass das entstehende Bild an eine möglichst neutrale Oberfläche geworfen wird, damit ein möglichst hoher Kontrast entsteht.
Durchführung
Um den Aufbau zu justieren, wird die Höhe des sich in Ruhe befindenden Federpendels als Referenzhöhe angenommen und der Motor auf diese angepasst, sodass die Kugel des Federpendels und der Stab im Bohrfutter des Motors auf gleicher Höhe liegen.
Nun wird das Federpendel zum Schwingen angeregt. Hierbei ist darauf zu achten, das Federpendel zunächst nach oben hin auszulenken. So lässt sich eine maximale Auslenkung bestimmen, indem man die Feder solange zusammendrückt, bis sich die gesamte Feder anhebt. So wird ein mögliches „Springen“ der Federaufhängung verhindert.
Schwingt nun das Federpendel, wird die Geschwindigkeit des Motor so variiert, dass sich die Schatten beider Kugeln synchron bewegen. Um eine ungefähre Motoreinstellung zu finden, empfiehlt es sich, mit Hilfe eines Exzenters die Resonanzfrequenz der Feder zu bestimmen (vgl. Versuch: Resonanz eines Federpendels), da diese identisch mit der Eigenfrequenz der Feder ist. Dieser Vorgang kann sehr zeitintensiv sein, da er stark von der Sensibilität des Motors abhängt. Ist diese zu grob, so lässt sich die passende Frequenz nur schwierig einstellen. Daher bietet sich ein sehr sensibler Motor an.
Ergebnisse und Auswertung
Bei korrekt eingestelltem Motor erkennt man zwei synchron verlaufende Schatten, die sich auf und ab bewegen (siehe Video). Dadurch lässt sich der mathematische Zusammenhang bestätigen. Um weiter in das Thema einzusteigen, wäre eine Analyse des Videos mit Hilfe eines Computerprogramms (z.B. Viana) sinnvoll.
Mit Hilfe der Winkelfunktionen lässt sich anhand der Abbildung 2 folgende Formel aufstellen:
Mit der Zeit variiert der Winkel . Also ergibt sich zu . Diese Abhängigkeit wird mit der Winkelgeschwindigkeit zu .
Damit ergibt sich für die allgemeine Schwingungsgleichung
,
welche durch das Videoanalyseprogramm Viana bestätigt werden kann.
Sicherheitshinweise
Um das Verletzungsrisiko zu vermindern, muss darauf geachtet werden, dass die Kugel an der Feder gut befestigt ist, um ein mögliches Ablösen zu verhindern. Zudem sollten alle möglichen Stoßkanten mit Hilfe von z.B. Styroporkugeln abgesichert werden. Zusätzlich sollte wie bei jedem Versuch, bei dem elektrische Geräte verwendet werden, die Stromzufuhr erst bei Beginn der Versuchsdurchführung eingeschaltet werden, um ein unabsichtliches Starten zu verhindern.
Siehe auch
Videoanalyseprogramm VIANA: http://www.didaktik.physik.uni-due.de/viana/