Messung der Erdbeschleunigung g (digital) mittels Video-/ Tonanalyse bzw. Lichtschranke
| Messung der Erdbeschleunigung g (digital) mittels Video-/ Tonanalyse bzw. Lichtschranke | |
| Kombinierter Messaufbau zur Bestimmung der Fallbeschleunigung mittels Video- und Tonanalyse, sowie über Lichtschranken | |
| Kurzbeschreibung | |
|---|---|
| Das Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung ohne Anfangsgeschwindigkeit, also auch des freien Falls, wird in einem kombinierten Aufbau verwendet um die Fallbeschleunigung g zu bestimmen. Dazu wird die Fallzeit durch drei verschiedene Methoden: Videoanalyse, Lichtschranken, Tonanalyse gewonnen. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 9, Sek. II usw. |
| Basiskonzept: | Wechselwirkung, Energie |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Josef Kaliski |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagener |
Die Bestimmung der Erd- bzw. Fallbeschleunigung wird in der Schule in der Regel über Ausnutzung des quadratischen Zusammenhangs des Fallweges und der Fallzeit vorgenommen. Wegen der sehr kurzen Fallzeit von bzw. bei Fallhöhen von bzw. ist das jedoch schwierig. Eine Möglichkeit dem zu begegnen ist der Rückgriff auf computergestützte Messtechnik. Für die notwendige Weg-Zeit-Messung gibt es verschiedene Möglichkeiten.
Der hier vorgestellte Aufbau kombiniert drei davon: 1.) Videoanalyse und 2.) parallele Zweipunktmessung mittels Lichtschranken, sowie 3.) Tonanalyse (ebenfalls als Zweipunktmessung). Er bietet sich damit, neben der -Bestimmung, sowohl zur Thematisierung von Messmethoden, als auch zur Untersuchung von Messunsicherheiten an.
Hauptziel dieses Artikels ist es, anhand eines Praxisbeispiels eine Einführung in den Umgang mit den - für den Physikunterricht sehr potenten, in der Ausbildung aber nicht oder kaum behandelten - Programmen CASSY, VIANA und AUDACITY zu geben.
Im Unterricht wird in den meisten Fällen nur eine der drei Methoden angewendet werden. Ziel dieses Artikels ist es deshalb zusätzlich, die in diesem Fall - die Bestimmung der Fallbeschleunigung also - geeigneteste bezüglich des Erkenntnisgewinns und der Messunsicherheit zu finden.
Inhaltsverzeichnis
Didaktischer Teil
Der Berliner Rahmenlehrplan BRLP sieht im Modul "P4 - Schneller werden und bremsen" die Behandlung der gleichmäßig beschleunigten Bewegung () und des zugehörigen Weg-Zeit-Gesetzes in der Klasse 9/10 vor. Die gleichförmige, also mit konstanter Geschwindigkeit () erfolgende, Bewegung wurde in der Regel bereits in der 8. Klasse behandelt. Insbesondere soll laut BRLP der "Freie Fall" als Beispiel einer gleichmäßig beschleunigten Bewegung behandelt werden [1]
.
Wie eingangs erwähnt liegt die Hauptschwierigkeit einer direkten Beobachtung bei den sehr kurzen Fallzeiten bei üblichen Streckenlängen von ≈. So dauert der (freie) Fall eines Körpers über lediglich
Die Wissenschaftsgeschichte brachte deshalb unterschiedliche Apparaturen hervor, um den freien Fall zu verlangsamen. Klassisch sind hierbei die, schon von Galileo Galilei genutzte, schiefe Ebene, so wie die Attwood'sche Fallmaschine.
Der vorgestellte Versuchsaufbau macht sich statt mechanischer Kniffe moderne Technik zunutze. Während die Lichtschranke bzw. Aufnahme akustischer Signale mittels Mikrophon und Computer lediglich eine adäquate Zeitmessung in der benötigten Größenordnung ermöglichen, erlaubt die Videoanalyse sogar das verlangsamte Wiedergeben der direkt beobachteten Bewegung.
Die SchülerInnen können mit eigenen Augen sehen, dass es sich beim freien Fall keineswegs um eine gleichförmige Bewegung handelt.
Doch die Möglichkeiten der Videoanalyse gehen noch weiter: Nach der digitalen Verfolgung (automatisch oder manuell durch Anklicken) des zu untersuchenden Objektes erstellen gängige Programme (wie bspw. VIANA) automatisch Weg-Zeit-, Geschwindigkeits-Zeit-, und Beschleunigungs-Zeit-Diagramme.
Das funktioniert im vorgestellten Fall zwar wegen der verwendeten Kamera nicht zuverlässig, dennoch kann durch Analyse des Weg-Zeit-Diagramms mit Hilfe des Weg-Zeit-Gesetzes erstens festgestellt werden, dass es sich beim freien Fall um eine gleichmäßig beschleunigte Bewegung handelt und zweitens wie groß die Fallbeschleunigung (an der Erdoberfläche) ist.
Die Möglichkeiten der Videoanalyse gehen so weit, dass ganze Unterrichtsgänge zur Einführung der Mechanik basierend auf dieser entwickelt wurden (vgl. [2])
.
Die parallele Verwendung drei verschiedener Messverfahren bietet außerdem Anlass zur vergleichenden Fehlerabschätzung. Möchte man den Schwerpunkt hierauf legen, bietet es sich an, im Rahmen des Moduls 9/10 P4 die Fallbeschleunigung mit einer der anderen genannten Methoden zu bestimmen und diesen Versuch erst im späteren Verlauf der Sek. II, wenn weiterreichende mathematische Kenntnisse vorhanden sind, durchzuführen.
Versuchsanleitung
Aufbau
Benötigt werden:
- 1 schwerer Stativfuss
- 2 Stativstangen von ca. 1m Länge (plus ggf. Verbindungsstück)
- 1 Winkelbefestigung
- 1 kurze Stativstange (etwas länger als die Lichtschranken)
- 1 Querholm (Vierkant mit Bohrung, o. ä.)
- Bindfaden
- 1 Feuerzeug
- 1 Massestück von ca. 100g (z.B. Zylinder mit Haken)
- 2 kleine Kugeln (~1cm Durchmesser)
- 2 Lichtschranken (Art.Nr.: 337 462) + 2 Datenkabel (für das Cassy-System)
- Cassy-Grundeinheit (Art.Nr.: 524 010) + Steckmodul Timerbox / Timer S(Art.Nr.: 524 034 / 524 074)
- Videokamera (Handy, o.ä.; wenigstens 30 Bilder/Sekunde)
- Mikrofon (zb Webcam, i.d.R. reicht Qualität für Videoaufzeichnung nicht aus)
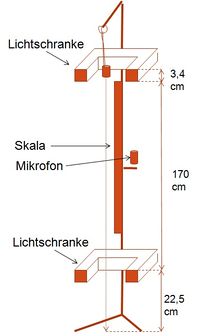
Der Aufbau an sich ist schlicht und recht schnell vorgenommen (vergleiche Abbildung rechts und Foto am Artikelanfang): In einen (schweren!) Stativfuss werden senkrecht zwei verschraubte Stativstangen von jeweils wenigstens einem Meter Länge gesteckt. Von oben wird nun zunächst die erste Lichtschranke aufgefädelt, dann ein Querholm zur Befestigung des Mikrophons, anschließend die zweite Lichtschranke und abschließend eine weitere Querstange zur Befestigung des Fallstücks. Für dieses erwies sich ein Metallzylinder () als gut geeignet. Zu letzt muss noch eine Skala angebracht werden. Viele Sammlungen halten hierfür mit Clips oder Magneten versehene Lineale bereit. Das Gewicht schließlich ist so zu befestigen, dass die obere Lichtschranke gerade noch nicht ausgelöst wird. Das verwendete Modell zeigt dies durch eine kleine LED an, die so lange leuchtet, wie der Lichtweg ununterbrochen ist. Um Schäden am Boden zu vermeiden sollte ein Kissen oder Ähnliches untergelegt werden.
Durchführung
Videoanalyse
Vor der Analyse ist das Video aufzunehmen. Im hier ausgewerteten Versuch wurde dazu eine handelsübliche Handycamera verwendet (Nokia 808, 30fps, full HD). Dabei ist die wesentliche Kennzahl die Anzahl der Bilder pro Sekunde (=fps, engl.: frames per second). Sie sollte keinesfalls unter 30 liegen, da (vgl. Auswertung) schon mit dieser Rate Abstriche in der Verwendung von VIANA zu machen sind. Die Kamera ist soweit wie möglich vom Versuch entfernt zu positionieren (falls vorhanden Zoom benutzen), und auf halber Höhe der gesamten Fallstrecke. Dadurch wird der Einfluss perspektivischer Verzerrung minimiert. Zudem sollte sie hochkant verwendet werden, um das zur Verfügung stehende Bild maximal auszunutzen. Der Zylinder sollte, von vorne betrachtet, neben der Skala und vor einem dunklen Hintergrund fallen um eine optimale Sichtbarkeit im Video zu gewährleisten. Deshalb sind die Lichtschranken etwas nach rechts verdreht.
Lichtschranke
Im vorgestellten Versuch wurde zur automatisierten Zeitmessung das Programm CASSY der Firma LD-Didaktik verwendet. Es bietet vielfältige Einstellungsmöglichkeiten, überfordert dadurch aber schnell den unerfahrenen Nutzer. Um die Einarbeitungszeit zu minimieren sind Versuchsbeispiele integriert, die neben Informationen zu den zu verwendenden Steckmodulen auch bereits die nötigen Voreinstellungen im Programm enthalten. Für die hier beabsichtigte Zeitmessung kann das Beispiel "Gleichförmige Bewegung zwischen zwei Lichtschranken" verwendet werden.
Zwar ist der Fall nicht gleichförmig, sondern gleichmäßig beschleunigt, die Zeitmessung funktioniert aber trotzdem.
Wurden das Beispiel geladen und die Lichtschranken wie vorgesehen mit dem CASSY-Modul verbunden, kann die Messung mit einem Klick auf den Stoppuhr-Button "Messung starten" (Kurzwahl: F9) in der oberen Leiste begonnen werden. Die Zeitmessung beginnt danach erst, sobald der Lichtweg der ersten Lichtschranke unterbrochen wird und endet, wenn dies auch bei der zweiten geschieht.
Tonanalyse
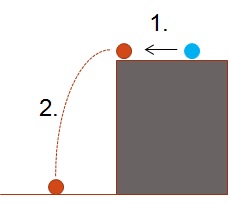
Hier wird statt des Zylinders eine Kugel als Fallkörper verwendet, welche an einer Kante positioniert (Hier: der Vorderkante der oberen Lichtschranke), durch eine Zweite angestoßen wird. Es entsteht ein "Klick"-Laut, der akustisch den Beginn der Fallzeit markiert. Das Auftreffen der Kugel verursacht ein weiteres Geräusch, wodurch das Ende des Falls deutlich wird.
Die Kugel muss so nah wie möglich an die Kante gebracht werden, sodass sie sich nach dem Stoß möglichst sofort im freien Fall befindet. Damit sie nicht ungewollt herunterfällt, sollte ein gelochtes Stück Papier untergelegt werden. Die Skizze macht deutlich, weshalb dieser Versuch nicht kombiniert mit den beiden anderen durchgeführt werden kann. Durch den Impulsübertrag von der anstoßenden Kugel erhält die Fallkugel eine horizontale Geschwindigkeitskomponente. Damit entspricht die Bahnkurve keiner senkrechten Strecke mehr, sondern einer Parabel. Diese ließe sich zwar durch Videoanalyse noch sehr gut erfassen. Das zielgenaue Treffen zweier Lichtschranken ist damit jedoch nahezu unmöglich, weswegen die Tonanalyse in einer gesonderten Durchführung erfolgen muss.
Wie schon die Kamera, ist auch das Mikrophon (integriert in Webcam von LOGITECH) auf halber Höhe anzubringen. Das verblüfft zunächst, wird durch folgende Rechnung jedoch deutlich:
In Luft beträgt die Schallgeschwindigkeit näherungsweise . Bei einer Fallstrecke von ergibt sich eine Fallzeit von , wenn man für die Erdbeschleunigung zu Grunde legt.
Angenommen das Mikrofon befände sich oben, also am Startpunkt des Falls, so würde das Akustische Signal für das Ende der Messung mit einer Verzögerung von detektiert werden. Die dann aus und errechnete Erdbeschleunigung wäre bereits um knapp 2% zu klein gegenüber dem verwendeten Referenzwert. Sollte der Versuch allerdings unter dem Gesichtspunkt der Unsicherheitsbetrachtung in den Unterricht integriert worden sein, könnte es lohnend sein, dass Mikrophon gerade am Start- oder Endpunkt zu positionieren. entspräche dann einem systematischen Fehler, der herausrechenbar ist. Ein schöner Anlass zwischen systematischen und statistischen Messunsicherheiten, die natürlich ebenfalls auftreten, zu unterscheiden.
Auswertung
Videoanalyse
Verwendung von VIANA
Zur Analyse des aufgenommenen Videos wurde das frei verfügbare Programm VIANA verwendet.
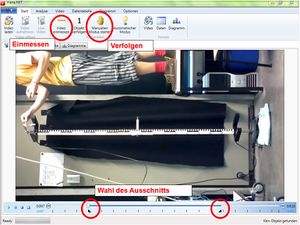
Ein Klick auf den Button "Video laden" lädt ein beliebiges Video in den gängigen Formaten. In der Zeitleiste unter dem Video kann durch verschieben der schwarzen Dreiecke der relevante Bereich eingegrenzt werden. Weil aber zum einen die Vorschau nicht (immer) zur Zeitleiste passt, und zum anderen diese Eingrenzung nicht mit gespeichert wird, empfiehlt es sich das Video zuvor mit einem anderen Programm (bspw. WINDOWS MOVIEMAKER) auf die benötigte Länge zu kürzen. Denn jede unnötige Minute bedeutet anschließend 30 zusätzliche Klicks bei der manuellen Objektverfolgung.
Jetzt kann der Maßstab durch einen Klick auf den Button "Video einmessen" festgelegt werden. Der Prozess wird durch eingeblendete Hinweise gut erklärt. Um die Messunsicherheit gering zu halten sollte jedoch nicht die Strecke des abgebildeten Lineals markiert werden (roter Pfeil im Bild), sondern die tatsächliche Fallstrecke des Zylinders (grüner Pfeil im Bild). Diese erscheint durch perspektivische Verzerrung etwas größer, entspricht aber ebenfalls den 170 cm.

Die Automatische Objektverfolgung funktionierte hier nicht. Also wird mit einem Klick auf "Manuellen Modus starten" die benutzergesteuerte Objektverfolgung begonnen. Hierbei geht ein weiteres Fenster auf und man klickt Bild für Bild auf die Stelle an der sich das Objekt befindet. Durch die endliche Belichtungszeit jedes Videobildes von Δ (30 Bilder werden pro Sekunde aufgenommen) und der zunehmend hohen Geschwindigkeit des Zylinders verschmiert dieser zu einem immer länger und dadurch immer blasser werdenden Streifen. Man hat nun zwei Möglichkeiten:
Entweder versucht man jedes Mal die Mitte des Streifens zu treffen, oder markiert jeweils den unteren Rand. Letzterer ist eindeutiger zu erkennen, weswegen hier die besseren Messergebnisse zu erwarten sind. Physikalisch macht es keinen Unterschied, weil die Wahl der Streifenmitte lediglich bedeutet, dass man jeweils die Mitte des Zeitintervalls Δ wählt, wohingegen der untere Rand dem Ende des Zeitintervalls Δ entspricht.
VIANA errechnet nun automatisch zu jedem Bild die Position des Zylinders in Metern (relativ zum frei wählbaren Ursprung, idealerweise der Ausgangslage des Zylinders). Unter dem Reiter "Diagramme" kann man sich dann verschiedene Graphische Darstellungen der Daten anzeigen lassen.
Da das Video quer aufgenommen wurde, entspricht die x-Koordinate aus VIANA hier der senkrechten Richtung, in der sich auch der Zylinder ausschließlich bewegt. Alle Abweichungen die in y-Richtung auftreten, sind Folge von Ungenauigkeiten bei der manuellen Verfolgung, weswegen jeweils nur die x-Komponente aller Größen zu betrachten ist.
Wie man in den Graphiken sieht, entspricht das Weg-Zeit-Diagramm als Einziges der Erwartung. Das liegt daran, dass das Geschwindigkeits-Zeit-Diagramm - die Ableitung des Weg-Zeit-Diagramms also - aus Differenzenquotienten, statt dem Differenzialquotienten, erstellt wurde. Bereits leichte Abweichungen der Messwerte von ihrem wahren Wert führen hier zu deutlichen Abweichungen von der Theorie. Beim Beschleunigungs-Zeit-Diagramm als Ableitung der Ableitung potentiert sich dieser Effekt.
Eine bessere Kamera, mit höherer Bildrate also, sollte hier deutlich bessere Ergebnisse erzielen. Zum Einen sinkt die Belichtungszeit pro Bild, was eine Verkürzung der auftretenden Streifen"verschmmierung" nach sich zieht und zum Anderen hätte man mehr Messwerte, sodass gerade im unteren Bereich für die einelnen Messwerte enger beieinander lägen. Aus Zeitgründen konnte nicht getestet werden, ob in diesem Fall die abgeleiteten Diagramme der Theorie entsprechen.
Unsicherheiten der Ausgangsgrößen Weg s und Zeit t
Die Unsicherheit der Wegbestimmung wurde mit abgeschätzt.
Bei der Zeitbestimmung ergab sich ein bemerkenswerter Effekt. Betrachtet man die von VIANA ausgegebenen Rohdaten (vgl. Abschnitt "Rohdaten"), so fällt auf dass der jeweilige Zeitstempel variiert - obwohl für beide Datenreihen die selbe Videodatei zu Grunde gelegt wurde! Zusätzlich treten Abweichungen sowohl absolut, als auch relativ (d.h. die unter dt eingetragenen Abstände zweier aufeinander folgender Zeitpunkte verändern sich in einem Rahmen von ungefähr ) auf. Aus diesem Grund wurde manuell ein Zeitstempel erzeugt. Dabei bekam das erste Bild die Zeit zugewiesen. In jedem weiteren Bild wächst um . Die Unsicherheit der Zeitmessung beträgt somit .
Bestimmung der Fallbeschleunigung g
Durch graphische Regression mit dem Weg-Zeit-Gesetz als Fitfunktion lässt sich die Fallbeschleunigung gewinnen. EXCEL (bzw. die Open-Source-Alternativen) liefert hierbei keine zufriedenstellenden Ergebnisse, da die Fitfunktion nicht selbstdefiniert werden kann. Stattdessen besteht einzig die Option mit einer quadratischen Funktion zu fitten. Diese verfügt dann aber auch über das lineare (entspricht: ), sowie konstante Glied (enstpricht:), was zu ernsthaften schlechten Werten für führt, weil und durch den Versuchsaufbau in guter Näherung verschwinden.
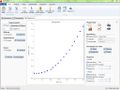
Folglich wurden die Fits mit QTI-PLOT vorgenommen:
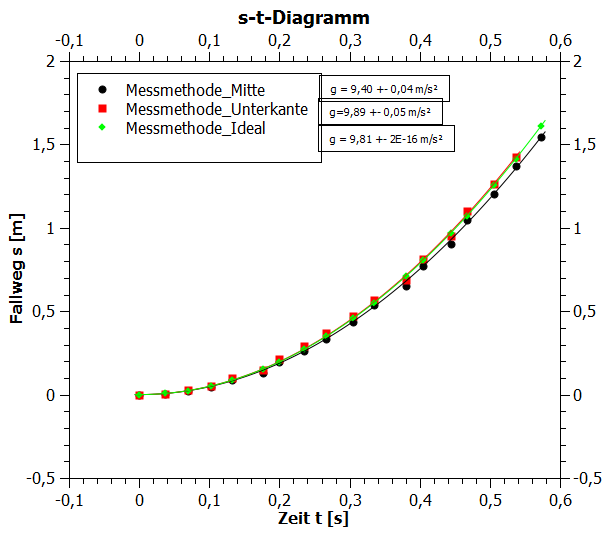
Um einen optischen Anzeiger für die Güte der Messergebnisse zu haben wurde eine Idealkurve (grün) mittels g=9,81 m/s² berechnet.Wie erwartet liegt die Kurve, deren Messwerte über die Unterkante bestimmt wurden (rot), näher an der Idealkurve, als die bei denen die Objektverfolgung über Anklicken der Mitte erfolgte (schwarz). Auffällig ist, dass bereits kleinste, kaum sichtbare Abweichungen der Graphen (vgl. rot-grün) zu deutlichen Abweichungen der berechneten Parameter, also führen. Offensichtlich liefert die Objektverfolgung über die Unterkante das bessere Ergebnis. Man erhält:
Lichtschranke
Unsicherheiten der Ausgangsgrößen Weg s und Zeit t
Während bei der Videoanalyse schon bei einfacher Durchführung des Versuchs mehrere Messwertepaare vorliegen, erhält man hier nur ein einziges, da es sich um eine Zwei-Punkt-Messung handelt. Deshalb muss der Versuch mehrfach durchgeführt werden. Der Mittelwert der Zeitmessungen ensptricht dann unserer Fallzeit , die Standardabweichung der zugehörigen Unsicherheit . Sechsfache Versuchsdurchführung ergab hier:
Die Fallstrecke entspricht jetzt dem Abstand der Lichtschranken zusammen mit der Höhe einer Lichtschranke . Es ergibt sich also insgesamt: . Der Abstand wurde mit dem Zollstock gemessen. Deshalb und weil nicht zu gewährleisten ist, dass der Aufbau absolut senkrecht steht, muss die zugehörige Unsicherheit mit ±1cm abgeschätzt werden.Sie überwiegt damit die der Höhenbestimmung der Lichtschranke mittels Messschieber deutlich, sodass angenommen werden kann:
.
Bestimmung der Fallbeschleunigung g
Durch Umstellen des Weg-Zeit-Gesetzes und Einsetzen erhält man die Fallbeschleunigung. Ihre Unsicherheit errechnet sich aus den Unsicherheiten und gemäß Gauß'scher Fehlerfortpflanzung über das umgestellte Weg-Zeit-Gesetz zu:
Tonanalyse
Verwendung von AUDACITY
Zur Aufnahme und Auswertung der Tonsignale wurden eine Webcam von LOGITECH mit integriertem Mikrophon und das frei verfügbare Programm ADACITY verwendet.
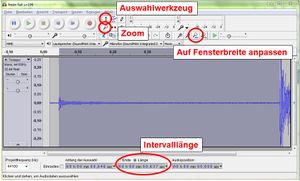
Dazu öffnet man AUDACITY. Die Webcam wird automatisch erkannt. Mit einem Klick auf den Aufnahme-Button wird eine neue Tonspur angelegt und die Aufnahme beginnt. Es bietet sich an, nicht benötigte Bereiche zu entfernen. Dazu markiert man diese und drückt die ENTF-Taste. Anschließend kann die Tonspur durch einen Klick auf den entsprechenden Button auf den auf Fensterbreite angepasst werden. Jetzt kann mit dem "Auswahlwerkzeug" ein Bereich in der Tonspur markiert werden. Dessen Länge wird unten direkt auf ms genau angezeigt. Wählt man als Anfang bzw. Ende jeweils den Beginn des zum Tonsignals gehörenden Ausschlag, entspricht die angezeigte Zeit der Fallzeit. Die Erfahrung zeigt, dass bereits hier recht valide Werte erzielt werden.
Um die Auswahl zu verfeinern, muss mit "Zoom" nach der groben Auswahl des Bereichs die Ansicht vergrößert werden. (Klickt man mit der Lupe auf die x- bzw. y-Skala wir nur in dieser Dimension vergrößert, Rechtsklick verkleinert wieder um eine Stufe). Mit dem "Auswahlwerkzeug" fährt man nun an die Grenzen des markierten Bereichs. Es erscheint eine Hand mit ausgestrecktem Finger. Mit gedrückter Linker Maustaste wird die entsprechende Grenze nun so verschoben, dass sie in der Mitte des ersten positiven Ausschlags liegt (vgl. Abbildungen).
- Detail
Unsicherheiten der Ausgangsgrößen Weg s und Zeit t
Die Fallstrecke <maht>s= 196 \pm 1 cm</math> muss hier von der Oberkante der oberen Lichtschranke bis zum Boden bestimmt werden und wurde mit einem Maßband vermessen.
Wie auch die Messung mittels Lichtschranken, entspricht die in diesem Abschnitt vorgestellte Methode einer Zweipunktmessung. Der Versuch ist deshalb mehrfach durchzuführen und die gemessenen Fallzeiten zu mitteln. Die Standardabweichung entspricht dann der Unsicherheit . Man erhält:
Bestimmung der Fallbeschleunigung g
Durch Umstellen des Weg-Zeit-Gesetzes und Einsetzen erhält man die Fallbeschleunigung. Ihre Unsicherheit errechnet sich aus den Unsicherheiten und gemäß Gauß'scher Fehlerfortpflanzung über das umgestellte Weg-Zeit-Gesetz zu:
Zusammenfassung der Ergebnisse und Fazit
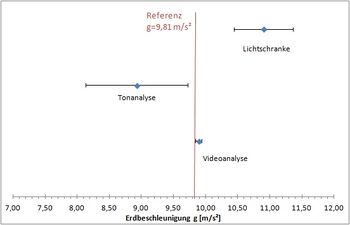
| Auswertungsmethode | Fallbeschleunigung g [m/s²] |
|---|---|
| Videoanalyse | 9,89 ± 0,05 |
| Lichtschranke | 10,9 ± 0,5 |
| Tonanalyse | 8,9 ± 0,8 |
Es fällt auf, dass keine der drei Messungen den Referenzwert von im einfachen Unsicherheitsintervall enthält. Vergegenwärtigt man sich jedoch, dass das einfache Unsicherheitsintervall nur mit 68%iger Wahrscheinlichkeit den Wahren Wert enthält stellt dies kein Problem dar.
Bezüglich der Messgenauigkeit liegt die Videoanalyse zunächst scheinbar vorn. Hier muss allerdings bedacht werden, dass ihr ca. 19 Messwertepaare zu Grunde liegen, während es bei den anderen beiden jeweils nur 6 sind. Mit jedem zusätzlichen Messwertepaar sinkt aber auch die Messunsicherheit. Es kann deshalb aus den vorliegenden Daten nicht grundsätzlich geschlossen werden, dass die Videoanalyse das genaueste Messverfahren darstellt.
Überhaupt lässt sich mit der Fallleiter (auch für CASSY erhältlich) mit sehr viel weniger Aufwand ein sehr viel genaueres Ergebnis erzielen. Hierbei wird ein in gleichmäßigen Abständen gelochter Metallstreifen senkrecht durch eine Lichtschranke fallengelassen. Man erhält bei diesem Versuch .
Noch genauere Ergebnisse lassen sich mit der Fallmaschine von ELWE (Art.nr.: U8400830) erzielen.
Dennoch zeigt der vorgestellte Versuch, dass sich mit jeder der drei vorgestellten Methoden brauchbare Messergebnisse erzielen lassen. Für die konkrete Aufgabenstellung "Ermittlung der Fallbeschleunigung g und Identifizierung des freien Falls als gleichmäßig beschleunigte Bewegung" ist sicherlich die Videoanalyse am geeignetesten, da hier die Bewegung von den SchülerInnen "verlangsamt" aber dennoch direkt als beschleunigt beobachtet werden kann (vgl. Abschnitt "Didaktische Analyse").
Rohdaten
Im Folgenden finden sich die den Berechnungen zu Grunde liegenden Rohdaten.
Videoanalyse
Es wurde das Video "Fall 1607" mit WINDWOS MOVIEMAKER gekürzt und anschließend wie beschrieben mittels VIANA ausgewertet.
Dabei ergaben sich folgende Daten:
| Zeitdifferenz dt [s] | Zeit t [s] (Mitte) | Weg s [m] (Mitte) | Zeitdifferenz dt [s] | Zeit t [s] (Unterkante) | Weg s [m] (Unterkante) |
|---|---|---|---|---|---|
| 0 | 0,028 | 0 | 0 | 0,025 | 0 |
| 0,03 | 0,058 | 0,00398425 | 0,037 | 0,062 | 0,00398425 |
| 0,034 | 0,092 | 0,02124935 | 0,033 | 0,095 | 0,0252336 |
| 0,038 | 0,13 | 0,04515487 | 0,032 | 0,127 | 0,05312338 |
| 0,028 | 0,158 | 0,08632549 | 0,031 | 0,158 | 0,09827825 |
| 0,045 | 0,203 | 0,12882419 | 0,044 | 0,202 | 0,15007355 |
| 0,022 | 0,225 | 0,19257225 | 0,023 | 0,225 | 0,21514968 |
| 0,034 | 0,259 | 0,26163264 | 0,035 | 0,26 | 0,28952241 |
| 0,033 | 0,292 | 0,33600537 | 0,032 | 0,292 | 0,37186365 |
| 0,033 | 0,325 | 0,43428362 | 0,038 | 0,33 | 0,46881382 |
| 0,035 | 0,36 | 0,53521804 | 0,03 | 0,36 | 0,56974824 |
| 0,034 | 0,394 | 0,64810522 | 0,046 | 0,406 | 0,68794776 |
| 0,037 | 0,431 | 0,77161708 | 0,024 | 0,43 | 0,8127877 |
| 0,033 | 0,464 | 0,90442552 | 0,04 | 0,47 | 0,95356465 |
| 0,028 | 0,492 | 1,04918673 | 0,022 | 0,492 | 1,10231011 |
| 0,033 | 0,525 | 1,20457261 | 0,039 | 0,531 | 1,26168025 |
| 0,034 | 0,559 | 1,37191126 | 0,031 | 0,562 | 1,42370655 |
Lichtschranke
Der zurückgelegte Weg wurde mit einem Maßband vermessen zu:
Sechsfache Durchführung ergab folgende Fallzeiten:
| Versuch 1 | Versuch 2 | Versuch 3 | Versuch 4 | Versuch 5 | Versuch 6 | |
|---|---|---|---|---|---|---|
| Zeit t [s] | 0,561 | 0,558 | 0,566 | 0,5696 | 0,5549 | 0,5707 |
Tonanalyse
Der zurückgelegte Weg wurde mit einem Maßband vermessen zu:
Sechsfache Durchführung ergab folgende Fallzeiten:
| Versuch 1 | Versuch 2 | Versuch 3 | Versuch 4 | Versuch 5 | Versuch 6 | |
|---|---|---|---|---|---|---|
| Zeit t [s] | 0,643 | 0,637 | 0,644 | 0,653 | 0,692 | 0,707 |
Literatur
- ↑ Senatsverwaltung für Bildung, Jugend und Sport Berlin: Rahmenlehrplan für die Sekundarstufe I - Physik, 1. Auflage, Berlin: 2006; Seite 45
- ↑ Martin Hopf, Thomas Wilhelm: Einführung in die Mechanik, 1. Auflage, Universität Würzburg, Ludwig-Maximilians-Universität München, Universität Wien: 2006; nur direkt erhältlich