Dynamischer Auftrieb und Strömungswiderstand - Messung mit der Einkomponentenwaage
| Dynamischer Auftrieb und Strömungswiderstand - Messung mit der Einkomponentenwaage | |
 Titelbild: Einkomponentenwaage zur Analyse der dynamischen Auftriebskraft | |
| Kurzbeschreibung | |
|---|---|
| Messung der dynamischen Auftriebskraft und des Strömungswiderstands mehrerer Probekörper mit einer Einkomponentenwaage | |
| Kategorien | |
| Mechanik, Strömungslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 9/10 (WP), Sek. II (Wahlthema) |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, Schülerdemoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Marek Mandel |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Dr. Ulrike Gromadecki-Thiele |
Bis in die 70er Jahre des 20. Jahrhunderts wurden zur Messung des Winddruckes sogenannte Einkomponentenwaagen verwendet (vgl. Brunstein et al.[1] (1977), S. 268). Ziel ist es, die auf einem von Luft umströmten Probekörper wirkende Kraft zu bestimmen. Die wirkende Kraft kann in die beiden Komponenten Strömungswiderstand und dynamische Auftriebskraft zerlegt werden. Mit der Einkomponentenwaage kann, wie der Name bereits verrät, jeweils eine der beiden Kraftkomponenten mittels des Hebelprinzips gemessen werden. Der Vorteil dieser Waage liegt darin, dass neben den Betrag der Kraft auch ihre Wirkrichtung sofort festgestellt werden kann.
Inhaltsverzeichnis
Didaktischer Teil
Fachliche Begründung im Physikunterricht
Die technische Nutzung von Luftströmungen ist aus unserem heutigen Alltag nicht mehr wegzudenken. Neben dem klassischen Thema "Fliegen" drängt seit einigen Jahren vermehrt das Thema "regenerative Energietechnik" und die damit verbundene Nutzung der Windenergie in den Vordergrund. Hierbei stellt sich die Frage, wie eigentlich moderne Windkraftanlagen funktionieren. Vielen Schülerinnen und Schülern ist lediglich der Luftwiderstand aufgrund ihrer Alltagserfahrungen (z.B. dem Gegenwind) bekannt. Ganz im Widerspruch dazu bewegen sich die Rotoren moderner Windkraftanlagen jedoch senkrecht zur Windrichtung.
Im Physikunterricht werden beide Themenfelder jedoch nur selten behandelt, obwohl sie von großer Gegenwarts- und Zukunftsbedeutung sind. Das Problem liegt hierbei in den unterschiedlichen Erklärungsansätzen für den dynamischen Auftrieb und dem oftmals noch nicht vorhandenen Fachwissen. Wodzinski[2] (1999) listet hierzu drei gängige Erklärungen auf:
- Der geläufige Ansatz ist der Druckunterschied zwischen der Ober- und Unterseite eines Tragflächenmodells. Die Form des Modells bewirkt, dass die Luft auf der Oberseite deutlich schneller vorbeiströmt als auf der Unterseite, wodurch sich nach der Bernoulli-Gleichung ein Über- und Unterdruck ausbildet.
- Oftmals wird auch die Rückstoßerklärung verwendet, welche sich auf das 3. Newtonsche Axiom (Wechselwirkungsprinzip) stützt. Da das Modell die anströmende Luft nach unten ablenkt, muss es nach dem Wechselwirkungsprinzip eine nach oben gerichtete Kraft erfahren.
- Als fachlich korrekte Erklärung wird dagegen der Vergleich mit einem rotierenden Zylinder angesehen. Zu der normalen Umströmung des Körpers muss zusätzlich eine Zirkulationsströmung beachtet werden, die aus den Wirbelbildungen an der Hinterkante des Modells (Anfahrwirbel) unter Berücksichtigung des Drehimpulserhaltungssatzes resultiert. Die Anfahrwirbel entstehen durch unterschiedlich schnelle Luftschichten. Schichten in der Nähe des Körpers werden durch Reibungseffekte stärker abgebremst. Eine ausführliche Erklärung kann in Demtröder[3] (2008), S. 251 ff nachgelesen werden.
Welcher Erklärungsansatz in der Schule verwendet werden sollte, hängt sehr vom fachlichen Stand der Schülerinnen und Schüler ab. Man sollte sich zudem die Frage stellen, wie tiefgründig und detailliert die Schülerinnen und Schüler das Prinzip des dynamischen Auftriebs verstehen sollen. Schauen wir uns nochmal die drei Ansätze genauer an: Der 1. Ansatz ist lediglich eine Schlussfolgerung aus dem 3. Ansatz. Er liefert keine Begründung für die Ausbildung des Druckunterschiedes. Auch der 2. Ansatz ist nicht ausreichend begründet, da die Ursache für die Ablenkung der Luft nach unten ungeklärt bleibt. Für die Sekundarstufe I bietet es sich daher an, die Erklärung nur mit Hilfe des Druckunterschiedes (1. Ansatz) zu führen. Der Ansatz ist fachlich korrekt und reduziert das Fachwissen nicht allzu stark. In der Sekundarstufe II kann dieser Ansatz wieder aufgegriffen werden und sich die Frage nach der Ursache für die unterschiedlichen Strömungsgeschwindigkeiten gestellt werden. Dies führt dann zur Anwendung des 3. Ansatzes. Hierbei muss beachtet werden, dass der Drehimpulserhaltungssatz zuvor thematisiert wurde. Der 2. Ansatz sollte nicht im Unterricht verwendet werden, da bei ihm nicht die grundlegenden Effekte zur Umlenkung der Luft angesprochen werden.
Bevor es jedoch zu einer Erklärung kommt, ist es im Sinne der Erkenntnisgewinnung wichtig, Beobachtungen an einem Luftstrom durchzuführen und alle auftretenden Kräfte auf ihre Abhängigkeiten hin zu untersuchen.
Methodisches Vorgehen
Da beide Versuche Grundlagen zur Strömungslehre mit Gasen vermitteln, sollten sie in einer Unterrichtsreihe möglichst zu Beginn durchgeführt werden. Um nun die Kraftwirkungen "sichtbar" zu machen, wird in beiden Versuchen auf das seit der Klassenstufe 7/8 bekannte Hebelgesetz mit der Bedingung, dass die Kräfte senkrecht zum Hebel stehen, zurückgegriffen. Dadurch kann auch die Wirkrichtung der Kraft sofort festgestellt werden und es stellt sich zudem heraus, dass die Masse des Probekörpers keinen Einfluss auf das Messergebnis hat. Die Wirkrichtung sollte vor der Versuchsdurchführung mit den Schülerinnen und Schülern besprochen werden. Nachteilig ist die zu berücksichtigende Umrechnung bei ungleicher Länge von Last- und Kraftarm. Dies kann jedoch sinnvollerweise für eine kurze Wiederholung des Hebelgesetzes genutzt werden. Es bietet sich ebenfalls an, mit den Schülerinnen und Schülern den Vorteil dieser Waage im Vergleich zu einem einfachen Federkraftmesser, der mit dem Probekörper in den Luftstrom gehalten wird, zu diskutieren.
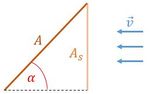
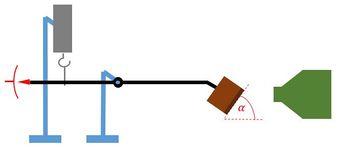
Beim Strömungswiderstand empfiehlt es sich, zuerst die Abhängigkeiten zur senkrechten Querschnittsfläche (bezogen auf den Luftstrom), zur Anströmgeschwindigkeit und zur Form durchzuführen, bevor der Anstellwinkel thematisiert wird. Eine Fläche wird daraufhin unter einem konkreten Winkel in den Luftstrom gehalten, deren senkrechte Projektion bereits zuvor vermessen wurde (siehe Abbildung 1). Eine einfache Begründung dazu wäre: Die strömende Luft nimmt die Fläche bei einem Anstellwinkel anders wahr, sie "erkennt" eine kleinere Fläche.
Beim Auftrieb sollte analog erst am Ende der Anstellwinkel thematisiert werden, allerdings müssen alle Messungen bereits unter einem konstanten Winkel zum Luftstrom erfolgen.
Versuchsanleitung zum Strömungswiderstand
Aufbau
Ein Vorteil des Experimentes liegt in seinem kostengünstigen Aufbau. Alle Materialien sollten in jeder Physiksammlung vorhanden sein. Für die Durchführung beider Versuche werden folgende Materialien benötigt:
- Luftstromerzeuger (z.B. Druckgebläse Leybold 373 041 oder Fön mit 1000 W Leistung)
- Federkraftmesser
- Windmesser (z.B. Anemometer Kaindl Windmaster 2 oder Prandtl-Sonde Leybold 373 10)
- Kugellager
- zweiseitiger Hebelarm
- Skala
- Zeiger
- Muffe mit Haken
- Stativmaterial
- verschiedene Probekörper (z.B. planare Körper aus Pappe, Tragflächenmodelle ...)
optional:
- Winkelskala
- Fadensonde
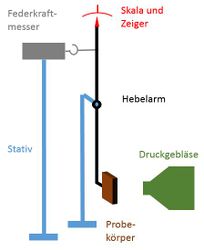
Der Aufbau erfolgt gemäß den beiden Abbildungen 2 und 3. Das Kugellager wird horizontal auf das Stativmaterial geklemmt und seine Achse falls nötig mit einer kleinen Stativstange erweitert. Anschließend wird auf diese Achse der Hebelarm vertikal befestigt. Als Hebelarm kann beispielsweise eine kleine, mittig durchbohrte Holzleiste verwendet werden. In Abbildung 3 wird der Hebelarm durch zwei Stativstangen gebildet, die an einer Muffe mit Gewinde festgeschraubt wurden. Am unteren Ende des Hebelarms wird eine Einspannvorrichtung für den Probekörper mittels Kreuzmuffe und Stativstab angebracht. Zur Messung des Anstellwinkels können optional eine selbstgebastelte Winkelskala an der Kreuzmuffe und ein kleiner Zeiger am Stativstab befestigt werden, wie es in Abbildung 3 zu erkennen ist. Der Federkraftmesser wird separat an einer neuen Stativstange horizontal gelagert und an den Haken der Muffe am oberen Ende des Hebelarms angehängt. Zur Verlängerung dieser Verbindung kann ein Faden verwendet werden. Weiterhin wird am oberen Ende ein Zeiger angebracht, die zugehörige Skala wird am hinteren Stativ befestigt. Zuletzt wird der Luftstromerzeuger auf Höhe des Probekörpers mit einem kleinen Abstand zur Messanordnung positioniert.
Durchführung
Bevor der Messvorgang gestartet wird, sollte sich die Waage im Gleichgewicht befinden. Dies kann mittels der Zeigerposition auf der Skala überprüft werden. Zum Austarieren der Waage kann der Federkraftmesser verwendet werden: Man bringt dazu die Waage in eine vertikale Lage und setzt anschließend den Federkraftmesser auf null. Falls dieser über keine Korrekturschraube verfügt, notiert man den angezeigten Wert als Offset. Der Probekörper wird anschließend eingespannt. Bevor die Messung gestartet wird, sollten die beiden Längen des Hebelarmes ausgemessen werden.
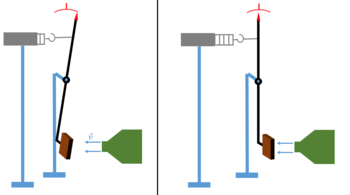
Es soll nun die Abhängigkeit des Strömungswiderstands von der Fläche und Form des Probekörpers, dem Anstellwinkel sowie der Anströmgeschwindigkeit untersucht werden. Beim Einschalten des Luftstromerzeugers kommt es aufgrund der wirkenden Widerstandskraft zur Auslenkung der Waage. Durch das Verschieben des Federkraftmessers kann die vertikale Ausgangslage wiederhergestellt werden (vgl. Abbildung 4). Am Federkraftmesser kann nun der Betrag einer Kraft abgelesen werden, die proportional zum Betrag des Strömungswiderstands ist.
Im Folgenden wird bei konstanten Parametern jeweils eine Variable verändert.
- Es können unterschiedlich große Plankörper senkrecht in den Luftstrom gehalten werden.
- Durch Variation der Leistung des Luftstromerzeugers kann die Anströmgeschwindigkeit verändert werden. Es empfiehlt sich, zuerst ohne Probekörper die Anströmgeschwindigkeit mit dem Windmesser zu bestimmen. Man halte dazu das Gerät auf Höhe der Einspannvorrichtung in den Luftstrom. Anschließend kann der Probekörper eingespannt und die Kraftmessung durchgeführt werden.
- Es können Probekörper mit verschiedener Form aber gleicher Fläche senkrecht in den Luftstrom gehalten werden. Zum Beispiel kann ein Vergleich zwischen hohlen Halbkugeln aus Plastik und Kreisscheiben, sowie Halbzylindern und Rechtecken erfolgen.
- Durch Verdrehen der Einspannung kann der Anstellwinkel des Probekörpers variiert werden. Man wählt hierzu am besten einen Winkel und eine Fläche aus, deren senkrechte Projektion zum Luftstrom bereits zuvor mit den Plankörpern vermessen wurde (siehe Abbildung 1 und Bemerkung bei Methodisches Vorgehen).
Messunsicherheiten
Quantifizierbare Messunsicherheiten
Die relative Messunsicherheit der Fläche kann allgemein mit angenommen werden, wenn die Plankörper aus Pappe selbst hergestellt wurden. Wird stattdessen beispielsweise eine quadratische Fläche mit der Länge und der Breite eines industriell hergestellten Modells mit einem Lineal abgemessen, so addieren sich die relativen Fehler: .
Die Messunsicherheit der Anströmgeschwindigkeit ist abhängig vom verwendeten Windmesser. Man beachte hierzu die entsprechenden Herstellerangaben. Für den durchgeführten Versuch wurde eine Prandtl-Sonde mit angeschlossenem U-Rohr-Manometer verwendet. Hier wurde allgemein die relative Messunsicherheit mit abgeschätzt.
Beim Federkraftmesser wurde für die Messunsicherheit der Widerstandskraft eine Skalenlänge verwendet.
Zuletzt ist noch der Strömungswiderstand der Einspannvorrichtung zu beachten, da auch diese teilweise vom Luftstrom erfasst wird. Um diesen systematischen Fehler zu umgehen, sollte man vor jeder Variation der Strömungsgeschwindigkeit einmal den Strömungswiderstand der Waage ohne Probekörper bestimmen. Der erhaltene Wert muss von jedem Messwert abgezogen werden.
Nicht-quantifizierbare Messunsicherheiten
Die vertikale Lage der Waage kann durch den Zeiger und der Skala zwar gut festgestellt werden, eine bessere Möglichkeit würde hier jedoch eine Wasserwaage bieten. Die Strömung ist nicht vollständig laminar hinter der Düse des Luftstromerzeugers. Weiterhin werden Reibungsverluste im Kugellager vernachlässigt.
Ergebnisse
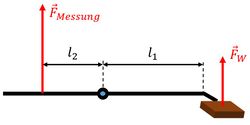
Die Waage befindet sich im Gleichgewicht, sowohl die am Federkraftmesser angreifende Kraft als auch die Widerstandskraft am Probekörper wirken senkrecht zum Hebelarm. Damit sind beide Kräfte proportional zueinander und können mit Hilfe des Hebelgesetzes umgerechnet werden: Seien wie in Abbildung 5 gezeigt und die Längen des Hebelarmes und der am Federkraftmesser abgelesene Wert, dann berechnet sich der Betrag des Strömungswiderstandes durch
- .
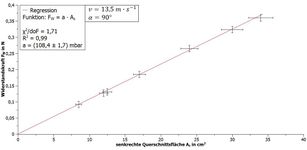
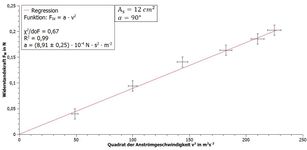
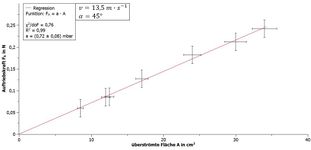
Die gemessenen Werte können nach der Umrechnung mit einem Analyse- und Visualisierungsprogramm (in den folgenden Beispielen mit QTI-Plot) verarbeitet und der jeweilige funktionale Zusammenhang grafisch dargestellt werden. In den Abbildungen 6 und 7 sind Beispielmessungen mit den entsprechenden Fitkurven dargestellt. In Tabelle 1 werden verschiedene Formen miteinander verglichen. Bei senkrechter Position des Plankörpers zum Luftstrom wurden die Parameter und gewählt, die Abhängigkeit vom Anstellwinkel wurde nur für den Winkel mit einer überströmten Fläche von gezeigt. Man beachte, dass alle Fitkurven zwangsweise durch den Ursprung verlaufen müssen. Um bei der Abhängigkeit von einen quadratischen Fit zu vermeiden, wurde hier die Darstellung in Abhängigkeit zu gewählt.
| Form | Strömungswiderstand | Form | Strömungswiderstand |
|---|---|---|---|
| hohle Halbkugel | hohler Halbzylinder | ||
| Kreisscheibe | Rechteckscheibe | ||
| hohle Halbkugel | hohler Halbzylinder |
Auswertung
Anhand der Fitkurven aus den Abbildungen 6 und 7 lässt sich schlussfolgern:
Bei einem Winkel von und einer Fläche von ergab sich der gleiche Widerstand wie bei einer senkrechten Fläche mit . Der Strömungswiderstand ist demnach nur abhängig von der senkrechten Querschnittsfläche. Die Form ist ebenfalls entscheidend für den Strömungswiderstand, wie aus Tabelle 1 hervorgeht. Bei der dem Luftstrom abgewandten Halbkugel bildet sich nur ein geringer Luftstau aus. Krümmt man nun die Fläche weiter dem Luftstrom entgegen, so steigt der Widerstand, was man bei der flachen Kreisscheibe aus Pappe erkennt. Der größte Widerstand tritt bei der Halbkugel mit Öffnung zum Luftstrom auf, da es hier innerhalb der Kugel zu einer massiven Luftanstauung kommt. Analog gilt dies für den Halbzylinder, wobei hier die Widerstandswerte aufgrund der nichtvorhandenen Radialsymmetrie größer sind.
Versuchsanleitung zur dynamischen Auftriebskraft
Aufbau und Durchführung
Der Aufbau ist auf dem Titelbild und in den Abbildungen 8 und 9 dargestellt und erfolgt analog zum vorherigen Aufbau zum Strömungswiderstand. Allerdings werden der Hebelarm horizontal und der Federkraftmesser vertikal gelagert. Die Skala kann gesondert an einem neuen Stativstab befestigt werden. In Abbildung 9 wurden noch zusätzlich Massestücke zum Austarieren an die Waage angehängt.
Die Durchführung des Versuches erfolgt analog wie bei der Durchführung zum Strömungswiderstand jedoch in einer horizontalen Lage. Es wird wieder bei konstanten Parametern jeweils eine Variable verändert.
- Es können unterschiedlich große Plankörper unter einem konstanten Winkel in den Luftstrom gehalten werden.
- Die Veränderung der Anströmgeschwindigkeit erfolgt analog zum Versuch zum Strömungswiderstand.
- Zur Untersuchung der Formabhängigkeit bietet sich ein Vergleich zwischen einem Tragflügelmodell und einem Plankörper mit gleicher Fläche an.
- Durch Verdrehen der Einspannung kann der Anstellwinkel des Probekörpers variiert werden. Auch hierfür bietet sich ein Vergleich zwischen einem Tragflügelmodell und einem Plankörper mit gleicher Fläche an.
Messunsicherheiten und Ergebnisse
Die Messunsicherheiten entsprechen den Angaben im Abschnitt Messunsicherheiten zum Strömungswiderstand. Lediglich beim Federkraftmesser wurde für die Messunsicherheit der Auftriebskraft zwei Skalenlängen verwendet, da hier die Gleichgewichtslage der Waage instabiler war.
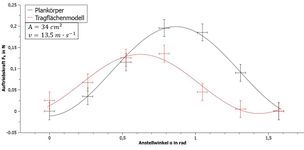
Die Umrechnung vom abgelesenen Wert zur wirkenden Auftriebskraft erfolgt analog zum vorherigen Versuch mit Hilfe des Hebelgesetzes (siehe hierzu den Abschnitt Ergebnisse beim Strömungswiderstand). In den Abbildungen 10, 11 und 12 sind Beispielmessungen mit den entsprechenden Fitkurven beziehungsweise Trendlinien dargestellt. Für den Plankörper wurden die folgenden Parameter gewählt: und . Analog zum Strömungswiderstand verlaufen alle Fitkurven für den Plankörper zwangsweise durch den Ursprung und es wurde bei der Abhängigkeit von ein quadratischer Fit vermieden. Bei der Winkelabhängigkeit wurde der Plankörper mit einem Tragflächenmodell verglichen. Die Trendlinie wurde eingefügt, da der Einsatz einer trigonometrischen Fitfunktion für den Unterricht zu aufwändig wäre.
Auswertung
Anhand der Fitkurven aus den Abbildungen 10 und 11 lässt sich schlussfolgern:
Betrachtet man zuerst nur den Plankörper in Abbildung 12, so erkennt man ein Maximum des dynamischen Auftriebes bei etwa 45°. Wird der Winkel zu groß gewählt, überwiegt der Strömungswiderstand aufgrund der Luftanstauung. Bei einem zu kleinen Anstellwinkel hingegen fließt die Luft ober- und unterhalb des Körpers annähernd gleich schnell vorbei, wodurch sich nach Bernoulli nur ein geringer Druckunterschied ausbildet.
Das Maximum des Tragflächenmodells wird dagegen bei einem deutlich kleineren Anstellwinkel erzeugt. Wird der Winkel hingegen zu groß gewählt, kommt es bereits hier schon aufgrund von Wirbelbildungen zum Strömungsabriss und damit zum Auftriebseinbruch. Bei kleineren Winkeln besitzt das Modell jedoch einen deutlich größeren Auftrieb als der Plankörper, da die Luft oberhalb des Modells schneller vorbeifließt und sich damit der Druckunterschied nach Bernoulli ausbildet.
Versuchserweiterungen
Aus den beiden Proportionalitäten kann jeweils die Proportionalitätskonstante ermittelt werden. Sie ist charakteristisch für die Form des Probekörpers und wiederum proportional zum empirischen Widerstandsbeiwert bzw. Auftriebsbeiwert . Konkret können diese Werte nur bei Kenntnis der Luftdichte berechnet werden. Die Abhängigkeit der beiden Kräfte von der Luftdichte kann durch den Vergleich beim Einsatz eines Föns und eines normalen Ventilators als Luftstromerzeuger überprüft werden. Man beachte jedoch, dass beide Geräte die gleiche Anströmgeschwindigkeit erzeugen müssen! Alternativ kann anstatt dieser experimentellen Betrachtung auch eine Einheitenbetrachtung durchgeführt werden, wodurch auf die Dimension einer Dichte geschlossen werden kann.
Um die Argumentation der Luftanstauung und Wirbelbildung zu unterstützen, kann zusätzlich der Strömungsverlauf am Probekörper mit Hilfe einer Fadensonde nachvollzogen werden. Die Fadensonde kann selbst gebastelt werden, indem ein dünner Faden (z.B. Lametta) an einem dünnen Stab geklebt wird. Die Sonde wird anschließend vor dem Probekörper in den Luftstrom gehalten. Der Faden folgt dem Verlauf der Stromlinien und kann daher mögliche Strömungsabrisse durch unregelmäßige Bewegungen nachweisen, wie es in Abbildung 13 zu erkennen ist (siehe auch Brunstein et al.[1] (1977), S. 297).
Sicherheitshinweise
Vor dem Einschalten des Luftstromerzeugers sind alle leichten Gegenstände (z.B. Papier) aus der Richtung der Öffnung des Gerätes zu entfernen oder gut zu befestigen! Die Leistung des Luftstromerzeugers sollte stets langsam erhöht werden!
Literatur
- ↑ 1,0 1,1 Brunstein, W. et al. (1977): Physikalische Schulversuche 3/4/5 - Mechanik der Flüssigkeiten und Gase; Volk und Wissen Volkseigener Verlag, Berlin
- ↑ Wodzinski, R. (1999): Wie erklärt man das Fliegen in der Schule? - Versuch einer Analyse verschiedener Erklärungsmuster; [1] Plus Lucis 2/99 [13.08.2014], VFPC - Verein zur Förderung des physikalischen und chemischen Unterrichts
- ↑ Demtröder, W. (2008): Experimentalphysik 1 - Mechanik und Wärme; 5. Auflage, Springer-Verlag, Berlin
Siehe auch
- Bestimmung der Umströmungsgeschwindigkeit an einem Tragflächenprofil im Nebelwindkanal
- Dynamischer Auftrieb und Strömungswiderstand - Messung im Windkanal