Dynamischer Auftrieb und Strömungswiderstand - Messung im Windkanal
| Dynamischer Auftrieb und Strömungswiderstand - Messung im Windkanal | |
 Windkanal der Fa. Leybold | |
| Kurzbeschreibung | |
|---|---|
| Messung von Auftriebskraft und Strömungswiderstand eines Tragflügelmodels im Windkanal | |
| Kategorien | |
| Mechanik , Strömungslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 9/10 (WP),
Sek. II (Wahlthema) |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Sabine Löhr |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Stephan Pfeiler |
In diesem Versuch werden Strömungswiderstand und Auftrieb einer von Luft umströmten Tragfläche im Windkanal gemessen. Das Experiment dient innerhalb einer Unterrichtsreihe zum Thema „Fliegen“ dazu, die beteiligten Kräfte zu verstehen und quantitativ zu erfassen. Als übergeordnetes Ziel soll der Versuch zum Aufbau eines tragfähigen und physikalisch korrekten Modells des Phänomens Fliegen beitragen.
Zur Herstellung eines praktischen Bezuges wird mit Hilfe der gemessenen Daten ein sogenanntes Polardiagramm nach Lilienthal erstellt. Die Darstellungsform wurde von Otto Lilienthal 1889 entwickelte und wird bis heute in der Strömungsphysik und Flugzeugtechnik benutzt. Sie stellt die physikalischen Ergebnisse des Experimentes in technisch aussagekräftiger Form dar und gibt Auskunft über Güte und Eigenschaften von Profilen bis hin zu ganzen Flugzeugen.
Inhaltsverzeichnis
Didaktischer Teil
Fliegen ist in der heutigen modernen Gesellschaft ein Alltagsphänomen. Trotzdem ist es erstaunlich: wie kann sich ein tonnenschweres Flugzeug scheinbar gegen die Gesetze der Schwerkraft in der Luft halten? Wenn es primäre Aufgabe des Physikunterrichtes ist, dem Schüler die Umwelt zu erschließen, dann muss diese Frage im Physikunterricht geklärt werden. Trotzdem wird das Thema Fliegen nur selten im Physikunterricht behandelt. Gründe liegen in scheinbar widersprüchlichen Erklärungsmodellen und in der Komplexität der Theorie. So sind beispielsweis Zirkulation oder Wirbelstärke nicht einfach didaktisch reduzierbar. Gerade deshalb ist es notwendig, sich dem Phänomen Fliegen über den experimentellen Weg der Erkenntnisgewinnung zu nähern.
Erkenntnisgewinnung: Beobachten-Interpretieren-Modellieren
Im vorgestellten Versuch werden die wichtigsten Gesetzmäßigkeiten behandelt, die das Fliegen verständlich machen: Auftrieb und Strömungswiderstand. Die Schülerinnen und Schüler unterstützen bei der Durchführung des Versuches und werten die Messdaten aus. Die Darstellung der Messdaten im Polardiagramm nach Lilienthal fordert eine praktische Interpretation der Ergebnisse heraus. Die im weiteren Verlauf der Unterrichtsreihe betrachteten Erklärungsmodelle zum Fliegen können vor dem Hintergrund der Versuchsergebnisse kritisch reflektiert werden.
Vorwissen:
- Grundlegende Kenntnisse aus der Mechanik (Druck, Kraft, Drehmoment, Strömung, Reibung)
- Begriffe der Strömungslehre (Medium, Kompressibilität und Inkompressibilität)
Ziele: (auch nach Rahmenlehrplan [1])
Die Schülerinnen und Schüler
- führen einfache Experimente zum Auftrieb durch
- kennen aerodynamische Kräfte am Tragflügel
- können erklären, wie Auftrieb und Strömungswiderstand vom Anstellwinkel abhängen
- recherchieren technische Daten von Flugzeugen zum Vergleich
Weitere mögliche Versuche innerhalb der Unterrichtsreihe:
Fachlicher Hintergrund
Strömungswiderstand
Der Strömungswiderstand Fw ist die Kraft, die auf einen umströmter Körper entgegengesetzt zur Bewegungsrichtung wirkt. Er setzt sich aus Reibungswiderstand und Druckwiderstand zusammen und ist von Dichte und Geschwindigkeit des anströmenden Mediums, von der Größe der Stirnfläche des umströmten Körpers und vom Winkel zwischen Körper und Anströmrichtung abhängig. Bei festem Winkel und Anströmgeschwindigkeiten, die nicht zu klein, aber unterhalb der Schallgeschwindigkeit liegen, lässt sich experimentell folgender proportionaler Zusammenhang zeigen:
.
Dabei bezeichnet die Dichte und die Geschwindigkeit des anströmenden Mediums sowie die Stirnfläche des umströmten Körpers. Die Größe bezeichnet man auch als Staudruck. Der Strömungswiderstand ist außerdem von Gestalt und Rauhigkeit des Körpers abhängig. Man bezeichnet diesen körperbezogenen Koeffizienten als seinen Widerstandsbeiwert cw in einem Medium und bestimmt ihn experimentell im Windkanal. Grundsätzlich ist der cw-Wert auch von der Reynoldszahl, der Machzahl und dem Turbulenzgrad der Strömung abhängig, für große Geschwindigkeiten im Unterschallbereich isotroper Medien (laminare Strömung) kann man aber einen festen Wert für feste Winkel annehmen. Damit ergibt sich die Widerstandsformel für umströmte Körper als
.
Auftrieb
Die dynamische Auftriebskraft FA ist die Kraft, die auf einen umströmter Körper senkrecht zur Bewegungsrichtung wirkt. Die bei der Umströmung eines angewinkelten bzw. unsymmetrischen Körpers entstehende Zirkulationsströmung verursacht unterschiedliche Strömungsgeschwindigkeiten ober- und unterhalb des Körpers. Nach Bernoulli bildet sich dadurch ein Druckunterschied zwischen Ober- und Unterseite und die resultierende Auftriebskraft lässt sich analog zum Strömungswiderstand schreiben als:
.
Den Koeffizienten cA nennt man Auftriebsbeiwert.
Polardiagramm
Charakteristisch für die Flugeigenschaften eines Körpers, speziell die eines Profils ist das Verhältnis von Auftrieb zu Strömungswiderstand. Bildet man den Quotienten aus beiden Größen, kürzen sich die meisten Größen fort und es verbleibt das Verhältnis der dimensionslosen Beiwerte cA zu cW. In einem Polardiagramm stellt man den Auftriebsbeiwert in Abhängigkeit vom Widerstandsbeiwert unter dem Parameter des Anstellwinkels (Winkel zwischen Anströmrichtung und Profilsehne) dar. Man erhält so eine für das Profil charakteristische Kurve, in der man verschiedene aerodynamische Kennwerte wie den Winkel für optimales Gleiten oder Steigen, den Maximalauftrieb oder geringsten Widerstand ablesen kann. Die Darstellung geht zurück auf Otto Lilienthal (1889) und wird bis heute in der Strömungsphysik und Flugzeugtechnik genutzt. Das Polardiagramm wird üblicherweise im verzerrten Maßstab cA:cW = 1:10 gezeichnet.
Versuchsanleitung
Aufbau
Material
- Windkanal (Leybold 373 12)
- Saug- und Druckgebläse (Leybold 373 042)
- Messwagen zum Windkanal (Leybold 373 075)
- Messzubehör 2 für Aerodynamik (Leybold 373 08)
- Sektorkraftmesser (Leybold 373 14)
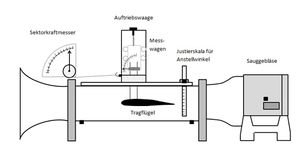
Versuchsaufbau
Der Windkanal wird mit Sauggebläse incl. Schutzgitter und Ansaugdüse nach Gebrauchsanweisung des Herstellers Leybold (Instruction Sheet)aufgebaut.
Der Messwagen wird auf die Laufschiene der Plexiglashaube des Windkanals aufgesetzt. Anschließend wird die Messstrecke waagerecht ausgerichtet, so dass der Messwagen in Ruhe verbleibt. Der Tragflügel wird in den Windkanal eingeführt und mit Hilfe der Haltestangen durch den Öffnungsschlitz des Windkanals am Messwagen montiert; der Tragflügel hängt nun an der Auftriebswaage. Die Spitzen der Haltestangen werden optisch mit der Nullpunktmarkierung auf der Skala des Messwagens zur Deckung gebracht, so dass der Tragflügel in der Waage hängt. Mit Hilfe der Rändelschraube am Messwagen wird zur Kompensation der Gewichtskraft des Tragflügels die Auftriebswaage auf Null justiert. Die Schnur des Sektorkraftmessers wird um die Umlenkrolle geführt und mit dem Messwagen verbunden, anschließend wird der Sektorkraftmesser auf Null justiert.
Nun wird die Anstellwinkelskala in den Windkanal eingehängt und justiert. Als Bezugspunkt verwendet man die Tragflügelspitze und verstellt die Anstellwinkelskala mit Hilfe der Rändelschraube zur Arretierung der Skalenplatte.
Durchführung
Bei maximaler Gebläseleistung werden der Auftrieb FA und der Strömungswiderstand FW des Tragflächenmodells bei unterschiedlichen Anstellwinkeln von -8° bis 14 Grad bestimmt.
Vor jeder Messung ist die Anstellwinkelskala aus dem Windkanal zu entfernen. Anschließend wird das Sauggebläse bei maximaler Leistung gestartet und 3 Minuten laufen gelassen, bis sich ein konstanter Luftstrom eingestellt hat. Nun können der Strömungswiderstand am linken Sektorkraftmesser und gleichzeitig der Auftrieb an der Skala der Auftriebswaage abgelesen und notiert werden.
Um den Anstellwinkel zu verändern, wird bei ausgeschaltetem Gebläse die Schraube an der linken Haltestange des Tragflügels im Messwagen gelöst und durch Verschieben des Stiftes wird mit Hilfe der Anstellwinkelskala der gewünschte Winkel eingestellt. Die Justierung der Auftriebswaage und des Sektorkraftmessers sind anschließend zu überprüfen und ggf. neu vorzunehmen.
Ergebnisse
In einer Messreihe wurden die nachfolgenden Werte aufgenommen:
| Anstellwinkel [°] | Strömungswiderstand [N] | Auftrieb [N] |
|---|---|---|
| -8 | 0,10 | -1,0 |
| -6 | 0,08 | -0,7 |
| -4 | 0,07 | -0,4 |
| -2 | 0,07 | -0,2 |
| 0 | 0,07 | 0,05 |
| 2 | 0,09 | 0,25 |
| 4 | 0,11 | 0,4 |
| 6 | 0,13 | 0,6 |
| 8 | 0,16 | 0,8 |
| 10 | 0,19 | 1,0 |
| 12 | 0,24 | 1,25 |
| 14 | 0,33 | 1,4 |
Auswertung
Fehlerbetrachtung
Die Einstellung und Ablesung des Anstellwinkels muss als größte Fehlerquelle angesehen werden, da die Skala sehr grob ist und der optische Vergleich mit der Profilsehne nur ungenau erfolgen kann. Es ist von einer Ablesegenauigkeit Δφ = ± 1° auszugehen. Die beteiligten Kräfte können mit einer Genauigkeit von delta Δ FA = ± 0,1° und Δ FWφ = ± 0,01° abgelesen werden. Als weitere Fehlerquellen sind die Reibungsverluste bei der Führung des Schlittens und der Aufhängung des Tragflügels in der Auftriebswaage zu berücksichtigen. Außerdem ist der Luftstrom auch nach der vom Hersteller angegebenen Einlaufzeit von 3 Minuten wahrscheinlich nicht absolut konstant und laminar. Unter Berücksichtigung der großen Fehleranfälligkeit ergeben sich trotzdem einigermaßen typische Diagramme für den Verlauf der beteiligten Kräfte. Für den Vergleich mit Literaturwerten siehe z.B. [2] oder [3].
Auftrieb
Der Auftrieb verläuft im gemessenen Winkelbereich nahezu linear. Der Verlauf ist charakteristisch für kleine Anstellwinkel, im weiteren Verlauf würde die Kurve im Winkelbereich des Ströumgsabrisses einen Scheitelpunkt erreichen und danach abfallen, analog im negativen Bereich.
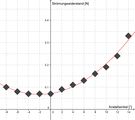
Strömungswiderstand
Der Verlauf des Stömungswiderstandes ist relativ typisch für ein asymetrisches Profil von relativ großer Dicke. Der Widerstand ist in der Nähe von Null Grad konstant gering und steigt bei betragsmäßig höheren Anstellwinkeln stark an. Literaturdiagramme sind in der Regel flacher, s. [2] [3].
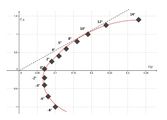
Polardiagramm
Die Darstellung cA(cW), die das Verhältnis von Auftrieb zu Stömungswiderstand unter dem Parameter des Anstellwinkels darstellt, ist annähernd typisch. Aus dem Diagramm kann man einen Gleitwinkel (Winkel, in dem ein Flugzeug im antriebsfreien Zustand nach unten gleitet) von fast 10° ablesen. Dieser Kennwert wäre praktisch extrem schlecht, ist jedoch bei der relativen Dicke des Profils und den fehlerbehafteten Messbedingungen plausibel. Literaturdiagramme verlaufen in der Regel länger nahe der y-Achse, s. [2] [3].
Sicherheitshinweise
Das Gebläse nur bei ordnungsgemäß aufgestecktem Schutzgitter und bei angesetztem Windkanal einschalten!
Literatur
- ↑ Rahmenlehrplan Physik für die Sekundarstufe I, 1. Auflage (2006), Senatsverwaltung für Bildung, Jugend und Sport, Berlin
- ↑ 2,0 2,1 2,2 Weltner, K. (2001): Flugphysik: Physik des Fliegens, Raketen, Satelliten; Aulis Verlag Deubner
- ↑ 3,0 3,1 3,2 Winkler, K. (1956): 25 Versuche zur Flugphysik; Volk und Wissen Volkseigener Verlag, Berlin