Corioliskraft vs. konstante Relativbewegung
| Corioliskraft vs. konstante Relativbewegung | |
 Coriolis-Relativ-Scheiben, Aufbau zum Vergleich zweier Perspektiven auf die radialen Bewegungen von Metallkugeln in einem rotierenden System | |
| Kurzbeschreibung | |
|---|---|
| Mit diesem Experiment soll qualitativ veranschaulicht werden, wie sich die in einem rotierenden Bezugssystem wirkende Corioliskraft für einen ruhenden Betrachter außerhalb des Systems darstellt. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 10, Sek. II |
| Basiskonzept: | System, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | LehrerInnen-Demontrations- oder SchülerInnen- bzw. Kleingruppen-Experiment; qualitativer Parallel-Simulationsversuch zur Vertiefung |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Benedikt Käsbach |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Daniel-Friedrich Zechlin |
Obwohl der von Newton angenommene absolute Raum nicht existiert, gelten alle drei Newton´sche Axiome per Definition in einem Inertialsystem (vgl. Wilhelm[1] (2016), S. 23), von dem aus betrachtet ein sich im rotierenden System nicht parallel zur Drehachse bewegender Körper eine zusätzliche konstante Geschwindigkeit relativ zum beschleunigten System besitzt, sobald eine zuvor diese verhindernde Zwangskraft erlischt. Diese Relativgeschwindigkeits-Komponente wird aus dem beschleunigten Bezugssystem heraus als beschleunigt und somit als Widerspruch zu den Newton´schen Axiomen wahrgenommen, solange man keine Scheinkräfte mitbetrachtet, die diese verursachen. Das Wirken von Scheinkräften kann folglich nur in beschleunigten Bezugssystemen beobachtet werden, was durch die Coriolis-Relativ-Scheiben (vom Autor benannter Aufbau des hier vorgestellten Experiments) für die Corioliskraft gezeigt werden soll. Die Corioliskraft berechnet sich nach der Formel
,wobei die Masse und die Geschwindigkeit des Körpers sind, der sich im mit der Winkelgeschwindigkeit rotierenden Bezugssystem nicht parallel zur Drehachse bewegt.
Inhaltsverzeichnis
Didaktischer Teil
Der aus den Alltagserfahrungen resultierende, nicht erklärungsbedürftige Normalfall ist für die SchülerInnen, dass ein Auto ohne Ausbrechen eine Kurve durchfährt und nur der Spezialfall, dass das Auto aus der Kurve ausbricht, scheint erklärungsbedürftig, wozu dann ohne Beachtung der eigenen Perspektive die Scheinkraft herangezogen wird (vgl. Wilhelm[1] (2016), S. 25). Dieses durch Alltagserfahrungen verursachte Durchmischen der verschiedenen Perspektiven macht sich auch in dem Bestreben bemerkbar, in einer Zeichnung fälschlicherweise Scheinkraft und Geschwindigkeit gemeinsam abbilden zu wollen (vgl. Wilhelm[1] (2016), S. 24).
Auf der Grundlage dieser Überlegungen, kann mit dem im Folgenden beschriebenen Aufbau, den der Autor "Coriolis-Relativ-Scheiben" nennt, vor Abschluss einer Lehreinheit, die das Auftreten von Scheinkräften während Kreisbewegungen behandelndt, sichergestellt werden, dass die Verwendung von Scheinkräften nur für einen Beobachter im beschleunigten Bezugssystem legitim und dort zur Wiederherstellung der Gültigkeit vor allem des ersten Newton´schen Axionms auch notwendig ist. Das erste Newton´sche Axiom besagt: "Ein Körper bleibt in Ruhe oder bewegt sich mit konstanter Geschwindigkeit geradlinig weiter, wenn keine resultierende äußere Kraft auf ihn wirkt." (vgl. Tipler[2] (2015), S. 103).
Die Coriolis-Relativ-Scheiben bilden dabei ein Modell der sich drehenden Erde, wobei nur eine große äquatornahe und eine deutlich nördlicher liegende Kreisscheibe abgebildet sind. Die nach dem Experiment parallel nebeneinander stehenden Perspektiven sollen schrittweise hintereinander nachvollzogen werden, um sie abschließend miteinander vergleichen zu können.
Das Ausführen als LehrerInnen-Demonstrations-Versuch bietet sich im klassischen lehrerzentrierten Unterricht an, was vom Autor nur als Ergänzung empfohlen wird. Das SchülerInnen- bzw. Kleingruppen-Setting sollte im Rahmen einer gebundenen partizipativen Planung, in der das Experiment als Lernstation Teil eines Lernzirkels ist, im Zentrum stehen (vgl. Kircher[3] (2009), S. 324).
Meine Kommilitonin Sara Merheji thematisiert in ihrem Vortrag "Ausbreitung des Lichts und Grenzflächen (Brechung und optische Hebung)" die Fehlvorstellung von SchülerInnen, der Sonne entgegen gucken zu müssen, um einen Regenbogen sehen zu können, die durch Alltagsvorstellungen, in denen Brechung mit Transmission in Verbindung gebracht wird, begründet sind.
Mein Kommilitone Niklas Sturm nutzt die Alltagsvorstellung, in der zum überwinden größerer Widerstände auch größere Anstrengungen nötig sind, zum Auslösen eines kognitiven Konflikts, wenn er im Rahmen seines Vortrags zum Thema "E-Lehre: Stromkreise" in einem Stromkreis, in dem ein handbetriebener Kurbel-Dynamo als Spannungsquelle dient, mit dem die Nennspannung nur sehr bedingt übertroffen werden kann, den Widerstand verringert, wodurch eine in Reihe geschaltete Lampe heller leuchtet und die Kurbel bei gleicher Frequenz schwerer zu bedienen ist.
Versuchsanleitung
Aufbau
Materialien für den Aufbau:
- Mobile-Cassy 2 (Leybold, Artikel-Nr.: 524 005)
- Timer-Box (Leybold, Artikel-Nr.: 524 034)
- 2x Gabellichtschranke (Leybold, Artikel-Nr.: 337 46)
- Experimentiermotor (Leybold, Artikel-Nr.: 347 35)
- Steuer- und Regelgerät zum Experimentiermotor (Leybold, Artikel-Nr.: 34736)
- Riemenübersetzung (ca. 10:1)
- Experimentiermotor, elektronisch geregelt, 230V~ (Phywe, Artikel-Nr.: 11030-93)
- 2x Drehlager (Phywe, Artikel-Nr.: 02845-00)
- 2x Drehteller (Bauhaus Artikel-Nr. 22937643 )
- Funkkamera Kamera Lupus Electronics/ Funkkamera Radcon – LE830 inkl. Empfänger
- Apple iPod Nano (alternativ zur Funkkamera zum Erhalten der Standbilder und für die Außenansicht)
- Stativmaterial
- Fixier-Muttern
- Metallschiene
- 2x Markierungsfahne/Haftzettel 20mm breit
- Metallkugeln
- Radiergummi
- Blumensteckmoos
- Pappe
- Flüssig-Klebstoff & breites Klebeband
- Verlängerungskabel mit Schalter
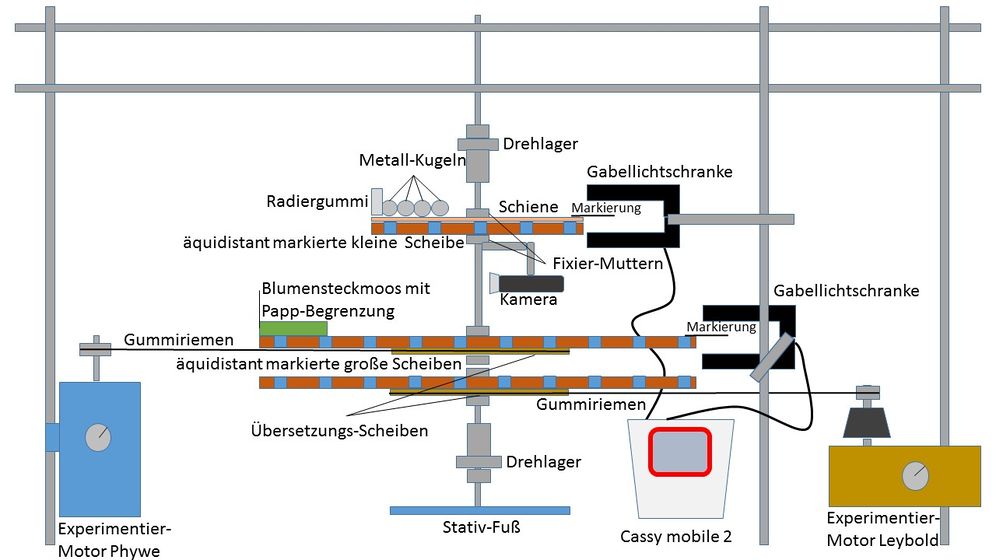
Die beiden Drehteller werden zerlegt, so dass man zwei identisch große Scheiben mit einem Loch im Mittelpunkt und zwei kleinere zentral durchbohrte Scheiben, von denen jedoch nur eine benötigt wird, erhält. Alle später verwendeten Scheiben erhalten eine äqidistante Randmarkierung. Die Abstände zwischen den Markierungen sollten mindestens 5 cm betragen.
Eine kleine und eine große Scheibe werden auf einer ca. 25 cm langen Stativstange, die einseitig ein ca. 20 cm langes Gewinde aufweist mit je zwei Fixier-Muttern in einem Abstand von ca. 15 cm zueinander befestigt, wobei die kleinere an die gewindefreie Zone grenzt. Die Zone ohne Gewinde dient der sicheren Befestigung im Drehlager, das wiederum mit den oberen beiden horizontal verlaufenden Stativstangen verbunden ist. Beim Fixieren der oberen kleinen Scheibe, wird je eine dünne Metall-Rundstange auf eine Seite der Mittelachsen-Stativstange zwischen Fixier-Mutter und Scheibe parallel zueinander verlaufend eingeklemmt, so dass Schienen entstehen auf denen sich die Metall-Kugeln reibungsarm, radial bewegen können. Gestoppt wird diese Bewegung bis zum gewünschten Beobachtungszeitpunkt durch ein eingeklemmtes Stück Radiergummi.
In Rotation versetzt werden kann dieser obere Teil vom Aufbau, das Erdkugel-Modell, über eine zwischen Unterseite der großen Holzscheibe und Fixier-Mutter eingeklemmten U-Profil-Scheibe, in deren Rand ein Gummiriemen Halt findet, der gleichzeitig um die Welle eines der beiden am Stativrahmen befestigten Experimentiermotoren gespannt ist, wodurch eine Rotations-verlangsamende Übersetzung von etwa 10:1 realisiert wird. Die Drehfrequenz-Senkung ist vor allem beim Experimentiermotor von Phywe relevant, da dieser bis zu 13.000 Umdrehungen pro Minute leisten kann. Dieser wird auch über ein Verlängerungskabel mit Schalter an das Stromnetz angeschlossen, da er selber keinen Ein- und Ausschalter besitzt.
An einer dritten vertikal ausgerichteten Stativstange, die an den oberen horizontal verlaufenden befestigt ist, montiert man nun zwei Präzisions-Gabellichtschranken, die die Bahngeschwindigkeiten der kleineren Scheibe des obigen Systems, Welches das Erdkugel-Modell darstellt und die der zweiten großen Scheibe messen, die als Vergleichssystem zur Veranschaulichung der Relativgeschwindigkeit dient. Die Lichtschranken sind dafür über eine Timerbox an das Mobile Cassy 2 angeschlossen, wodurch die eigentlich gemessene Dunkelzeit beim Durchlauf einer auf die entsprechenden Scheiben zu klebenden Markierungsfahne (Haftzettel, 20 mm Breite) mit bekannter Breite als Bahngeschwindigkeit ausgegeben werden kann. Dem Autor war es nicht möglich die potentiell vorhandene Funktion des gleichzeitigen Messens beider Bahngeschwindigkeiten zu nutzen, weshalb das Umstecken der Lichtschranken von Nöten war.
Der untere Teil des Aufbaus, das Vergleichssystem, ist analog zum Erdkugel-Modell gestaltet. Die Unterschiede bestehen in der Befestigung im Stativfuß, dem Vorhandensein von nur einer Scheibe, welches die große ist und dem Fehlen von Schienen.
Der obere Aufbau, wird abschließend mit knapp an der Mittel-Stange vorbei schauender Kamera und Kugel-Auffang-Vorrichtung, die aus Blumensteckmoos und Pappe besteht, ausgestattet, so dass die im rotierenden System beobachtete Abweichung von der radialen Ausgangsrichtung videotechnisch festgehalten werden kann. Abbildung 1 zeigt den schematischen Aufbau.
Durchführung
Nachdem sicher gestellt worden ist, dass die Rotation des gesamten Systems ungehindert möglich und die entsprechende Lichtschranke angeschlossen ist, versetzt man das Erdkugel-Modell in Rotation, was am besten mittels Experimentiermotor von Phywe geschieht, da dieser bei jedem Anschalten neu eingestellt werden muss. Es wird für die Bahngeschwindigkeit der einer halben Umdrehung pro Sekunde entsprechende, zuvor errechnete Wert eingestellt. Der Motor von Phywe wird ausgeschaltet, die untere Lichtschranke angeschlossen und der Experimentiermotor von Leybold, der das Vergleichssystem antreibt angeschaltet. Wenn die Vergleichs-Scheibe sich mit der selben Bahngeschwindigkeit dreht wie die obere kleine Scheibe des Erdgugel-Modells, kann der Motor kurz aus und wieder eingeschaltet werden um sicher zu stellen, dass der Wert relativ unverändert bleibt. Nun wechselt man bei still stehendem Gesamtsystem den Lichtschranken-Anschluss ein letztes Mal, um den Sollwert des Erdkugel-Modells erneut einzustellen und schließlich durch Hinzuschalten der Vergleichs-Scheibe das Bestehen einer Relativgeschwindigkeit zu überprüfen.
Um die Perspektive eines im rotierenden System befindlichen Beobachters einnehmen zu können, greift man auf die Bilder der Funkkamera zurück, wenn man das Geschehen in Echtzeit verfolgen möchte. Man wählt dafür auf dem Funkempfänger, der an einem Video-Wiedergabegerät, was hier ein Beamer war, angeschlossen sein muss, den gleichen Kanal aus wie auf der Funkkamera. Nun löst man das Radiergummistück aus der Schiene, sobald der Sollwert von einer Umdrehung pro Sekunde (0,3 m/s Bahngeschwindigkeit an der kleinen Scheibe gemessen) erreicht ist und stellt fest, ob die Kugeln eine bestimmte vorher mathematisch ermittelte Grenze der Abweichung nicht überschritten haben und wiederholt das ganze mit doppelter Rotationsfrequenz, also einer Umdrehung pro Sekunde (0,6 m/s Bahngeschwindigkeit an der kleinen Scheibe gemessen). Wenn man jedoch die seitliche Ablenkung der sich anfänglich radial von der Drehachse weg bewegenden Metallkugeln im freien Fall der Kugeln festhalten will, muss das Bildsignal aufgezeichnet und nachbereitet werden, was hier aus Bildqualitätsgründen mithilfe eines an der Funkkamera provisorisch fixierten iPods Nano und VLC Media Player umgesetzt wurde.
Ergebnisse
| Video: Demonstration des Perspektiven-Wechsels
mit den Coriolis-Relativ-Scheiben |
Die kleine Scheibe des Erdkugel-Modells und die große Vergleichs-Scheibe haben durch das Abstimmen aufeinander mithilfe der Lichtschranken die gleiche Bahngeschwindigkeit. Das repräsentiert die unveränderten radialen und tangentialen Relativgeschwindigkeiten der Metallkugeln, die vom Verlassen der kleineren Erdkugel-Modell-Scheibe bis zum Aufschlag im Blumensteckmoos am Rand der größeren, äquatornahen Scheibe des selben Modells bestehen. Auf dieser Grundlage ist anhand der unterschiedlichen Frequenzen der Punktmarkierungen auf den Rändern der beiden großen Scheiben ersichtlich, dass die Metall-Kugeln während ihrer gesamten Fallzeit konstante Relativgeschwindigkeiten bezogen auf den Aufschlagspunkt im Blumensteckmoos besitzen, von der die tangentiale Komponente, die zur Erklärung der Ablenkung bedeutende ist. Diese Betrachtungen können ausschließlich von einem Beobachter gemacht werden, der sich im Inertialsystem befindet.
Die durch die Nachbereitung des mit dem iPod aufgenommenen Videos entstandenen zwei Standbilder lassen nur indirekt, theoretisch auf eine beschleunigte Bewegung der Ablenkung schließen, die bei Annahme einer wirkenden ScheinKRAFT, hier der CoriolisKRAFT gegeben sein muss, durch welche die Gültigkeit des ersten Newton´schen Axioms aus der Perspektive des mit rotierenden Beobachters wieder hergestellt wird. Die Standbilder geben leider keinen mit bloßem Auge erkennbaren quadratisch wachsenden Zusammenhang zwischen der Ablenkung und dem Abstand zur Drehachse wieder, was am Blickwinkel der Aufnahme und der zeitlichen sowie räumlichen Auflösung liegen kann. Vielmehr legen diese Bilder leider eher einen linearen Zusammenhang nahe.
Auswertung
Die radiale Geschwindigkeitskomponente mit der die Kugeln die obere kleine Scheibe verlassen, kann nach Dankert mit einem einfachen Differential-Gleichungs-Ansatz errechnet werden (vgl. Dankert[4] (2006), S. 494f.). Die tangentiale Komponente dieser Geschwindigkeit ist gleich der Bahngeschwindigkeit des Randes der kleinen Scheibe, die sich rechnerisch über ergibt, und mit der Lichtschranke gemessen ca. 0,3 m/s für eine halbe Umdrehung pro Sekunde und ca. 0,6 m/s für eine ganze Drehung pro Sekunde beträgt. Setzt man in die Formel zur Berechnung der Bahngeschwindigkeit einmal den Radius der kleinen und zum anderen den Radius der großen Scheibe ein und zieht die zuerst erhaltene von der zuletzt erhaltenen Bahngeschwindigkeit ab, so erhält man rechnerisch die tangentialen Geschwindigkeiten der Metallkugeln relativ zum Rand der großen Scheibe des Erdkugel-Modells. Die dadurch bedingte Ablenkung ergibt sich aus der Multiplikation mit der entsprechenden Fallzeit. Aus der inneren Perspektive eines im rotierenden System befindlichen Beobachters erzeugt die Corioliskraft die bei radialer Ausgangsbewegung entstehende tangentiale Relativbewegung, die somit aus dieser Perspektive als beschleunigt wahrgenommen werden muss. Um den Eindruck einer beschleunigten Bewegung besser nachweisen zu können, sollte man ein Videoanalyse-Programm verwenden und evtl. die Winkelgeschwindigkeit erhöhen. Mit solch einem Programm, ließe sich dann auch in der Draufsicht aus dem Inertialsystem heraus die konstante geradlinige Relativgeschwindigkeit besser nachvollziehen, was hier aus Zeitgründen nicht mehr umgesetzt werden konnte.
Sicherheitshinweise
- Es ist auf eine übersichtliche Kabelführung zu achten.
- Schwere und/oder kostbare Geräte sind vor dem Herunterfallen zu sichern.
- Der Experimentiermotor von Phywe, der bis 13.000 Umdrehungen pro Minute realisieren kann, sollte mit Fingerspitzengefühl in Betrieb genommen und der doch recht schwere Aufbau dabei mit einem leichten als Starthilfe dienenden Schwung manuell in Drehung versetzt werden, da sonst durch lang andauernden starken Stromfluss Kabel durchbrennen können.
Literatur
- ↑ 1,0 1,1 1,2 Wilhelm, T. (2016): Plus Lucis 2/2016 - Physikdidaktik : Trägheitskräfte im Mechanikunterricht; Verein zur Förderung des physikalischen und chemischen Unterrichts, Wien
- ↑ Tipler, P.; Mosca, G., Wagner, J. (Hrsg.) (2015): Physik: für Wissenschaftler und Ingenieure - 7. deutsche Auflage; Springer-Verlag, Berlin Heidelberg
- ↑ Kircher, E.;Girwidz, R.; Häußler, P. (2009): Physikdidaktik: Theorie und Praxis - 2. Auflage; Springer-Verlag, Berlin Heidelberg
- ↑ Dankert, J.; Dankert, H.(2006): Technische Mechanik:Statik, Festigkeitslehre, Kinematik/Kinetik - 4. Auflage; B. G. Teubner Verlag / GWV Fachverlage GmbH, Wiesbaden