Coriolisbrunnen
| Coriolisbrunnen | |
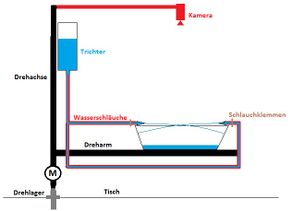
 Titelbild: Versuchsaufbau für den Coriolisbrunnen | |
| Kurzbeschreibung | |
|---|---|
| Die Auswirkung der Corioliskraft soll anhand eines bewegten Wasserstrahles in einem rotierenden System qualitativ verdeutlicht werden. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 10, Sek. II |
| Basiskonzept: | System, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, Schülerdemoexperiment |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Stefan Staroske |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Beschreibt man Bewegungen als Beobachter in einem rotierenden und damit beschleunigten Bezugssystem, ist man auf die Einführung von Scheinkräften angewiesen, da das beobachtete System kein Inertialsystem ist. Bewegt sich der zu beobachtende Körper in einem rotierenden System, führt man neben der Zentrifugalkraft auch die Corioliskraft als Scheinkraft ein. Diese wirkt auf Körper, die sich nicht parallel zur Drehachse des Systems bewegen. Die Corioliskraft wirkt zum Beispiel auf sich radial zur Drehachse des Systems hin bewegende Körper in Richtung der Drehung und bei sich radial von der Drehachse entfernenden gegen die Drehrichtung:
Dabei ist die Masse des zu beobachtenden Körpers, die Geschwindigkeit dieses Körpers im rotierenden Bezugssystem und die Winkelgeschwindigkeit, mit der das System rotiert.
Der Coriolisbrunnen veranschaulicht qualitativ einfach das Phänomen und die Notwendigkeit der Einführung der Corioliskraft.
Inhaltsverzeichnis
Didaktischer Teil
Der Coriolisbrunnen kann zur Verifizierung eines Teils der Theorie für das Einführen von Scheinkräften in beschleunigten Bezugssystemen eingesetzt werden, was einem deduktiven Unterrichtsprinzip bzw. einer deduktiven Erkenntnisgewinnung entspricht. Letzteres meint ausgehend von einer allgemeinen Theorie ein spezielles Phänomen bzw. den Ausgang eines speziellen Experimentes vorherzusagen.
Nach Popper wird das hypothetisch-deduktive Verfahren als angemessene Beschreibung des naturwissenschaftlichen Erkenntnisprozesses betrachtet: „Aus der vorläufig unbegründeten Antizipation, dem Einfall, der Hypothese, dem theoretischen System, werden auf logisch-deduktivem Weg Folgerungen abgeleitet; diese werden untereinander und mit anderen Sätzen verglichen, indem man feststellt, welche logischen Beziehungen zwischen ihnen bestehen.“ (vgl. Popper[1] (1976), S. 3). Weiter stellt sich nach Popper das hypothetisch-deduktive Verfahren wie folgt dar: "Die Erkenntnisgewinnung beginnt z.B. mit einer wissenschaftlichen Hypothese, aus der unter Einschluss von Randbedingungen einzelne Aussagen(Basissätze) gewonnen werden, die durch Beobachtung falsifizierbar sein müssen." (vgl. Kircher/ Girwidz/ Häußler[2] (2000), S. 137).
Einige Jahre vor Popper definiert Haspas die deduktive Methode den Physikunterricht zu gestalten wie folgt: „Das typische Merkmal der deduktiven Methode ist, dass sie eine mehr oder weniger große Anzahl von Einzelerkenntnissen entweder aus einer Allgemeinerkenntnis ableiten oder in einer systematisierenden Zusammenschau erscheinen lässt.“ (vgl. Haspas[3] (1969), S. 119).
Auf das vorliegende Experiment zum Coriolisbrunnen meint dies folgendes: Ausgehend von der in der Schule gelernten und somit bekannten Theorie über Scheinkräfte in rotierenden Bezugssystemen (Zentrifugal- und Corioliskraft) werden Voraussagen über das Verhalten der Wasserstrahlen im Coriolisbrunnen getroffen. Die Durchführung des hier beschriebenen Experimentes dient damit der Prüfung der allgemeinen Theorie anhand des Phänomens der Wasserstrahlen, die im Coriolisbrunnen abgelenkt werden.
Der Coriolisbrunnen ist ein Modell eines rotierenden Bezugssystems. Mit dem Brunnen kann die seitliche Ablenkung von Körpern, die sich im rotierenden Bezugssystemen bewegen, untersucht und erklärt werden.
Versuchsanleitung
Aufbau
Materialien für das Experiment:
- Drehlager Phywe 02845.00
- Tischhalterung für das Drehlager
- Zylinderförmiger Trichter mit ca. 1 Liter Fassungsvermögen
- 3 Gummischläuche je ca. 60 cm lang
- Schlauchteiler
- 2 Schlauchverbinder mit kleinem Austrittsquerschnitt
- 2 Schlauchklemmen
- Kunststoffwanne ca. 25 cm breit, 5cm hoch und 15cm tief
- Funkkamera Kamera Lupus Electronics/ Funkkamera Radcon – LE830 inkl. Empfänger
- Bildbearbeitungsprogramm: K-Vox Mini USB Movie Editor mit ShowBiz DVD2
- Experimentiermotor mit Drehzahlsteuerung Phywe 11030.93
- Getriebe 30:1 Phywe 11029.00
- Stativmaterial
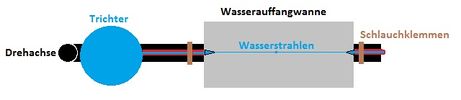
In den Abbildungen 1 und 2 ist der Aufbau schematisch dargestellt: An einer Tischkante wird das Drehlager mit einer Tischhalterung befestigt. Der Antriebsriemen für den Motor wird vor dem weiteren Aufbau um das Drehlager gelegt.
In der Drehachse des Lagers wird eine Stativstange montiert. Am oberen Ende dieser Stange wird ein zylinderförmiger Trichter mit einem Fassungsvermögen von ca. 1 Liter Wasser befestigt. Vom Trichterboden geht ein Schlauch ab. Dieser Schlauch wird mittels Schlauchteiler in 2 weitere Schläuche überführt. Am Ende der beiden Schläuche befestigt man 2 Schlauchverbinder mit einem sehr keinen Austrittsquerschnitt (als „Wasserdüsen“).
Möglichst weit unten an der Stativstange wird die Kunststoffwanne zum Auffangen des Wassers aus den Düsen befestigt. An dieser Wanne werden an zwei gegenüberliegenden Wänden die zwei Schlauchenden mit den Schlauchverbindern befestigt, sodass eine Düse radial von der Drehachse weg und eine Düse zur Drehachse hin zeigt.
Vor jeder Düse wird eine Schlauchklemme angebracht, sodass die Düsen einzeln geöffnet und geschlossen werden können.
Die Düsen werden so justiert, dass sich die Wasserstrahlen bei offenen Schlauchklemmen ohne Rotation des Systems über der Mitte der Auffangwanne treffen (Siehe Abbildung 2). Ist nur eine Düse geöffnet, soll der Strahl die Mitte der gegenüberliegenden Wannenwand treffen.
Bei der Durchführung des Experimentes hat sich herausgestellt, dass es sich empfiehlt, den Höhenunterschied des Anfangswasserstands im Trichter zu den Wasserdüsen an der Auffangwanne auf mindestens 50cm einzustellen, da sonst die Wasserstrahlen die gegenüberliegende Wannenwand nicht erreichen.
Der Motor wird am Tischrand in geeignetem Abstand befestigt, sodass der Antriebsriemen genug Spannung aufweist, damit dieser nicht von den Antriebsrädern des Motors und des Drehlagers rutscht.
Zuletzt wird bei Bedarf die Kamera wie in der Abbildung 1 über der Wasser-Auffangwanne angebracht. Die Kamera dreht sich mit dem System mit und wird so justiert, dass Sie die gesamte Plastikwanne mit den beiden Wasserstrahlen im Bild hat.
Modifikationen
- Wenn kein Motor vorhanden ist, kann dieser auch weggelassen werden. Dann kann jedoch nur die Ablenkrichtung des Wasserstrahls zuverlässig bestimmt werden. Die Stärke der Ablenkung in Abhängigkeit der Drehgeschwindigkeit und Geschwindigkeit der Wasserstrahlen können dann nur wage wahrgenommen werden.
Die Nutzung eines Motors ist jedoch empfehlenswert, da mit dessen Hilfe konstante und unterschiedliche Drehgeschwindigkeiten des Brunnens umgesetzt werden können.
- Die Geschwindigkeit des aus den Düsen kommenden Wassers kann durch höher oder tiefer hängen des Trichters verändert werden.
Durchführung
Der Trichter wird mit Wasser gefüllt. Die beiden Düsen werden vor dem Anschalten des Motors geöffnet. Im Folgenden können unterschiedliche Drehzahlen am Motor (also des drehenden Systems) eingestellt werden. Die Drehrichtung des Motors kann verändert werden.
Für das Video wurden zuerst mit der Drehrichtung im Uhrzeigersinn (Im Video am blauen Pfeil erkennbar) drei unterschiedliche Geschwindigkeiten realisiert und folgend zwei unterschiedliche Geschwindigkeiten gegen den Uhrzeigersinn.
Ergebnisse
| Video: Beobachtung im rotierenden Bezugssystem |
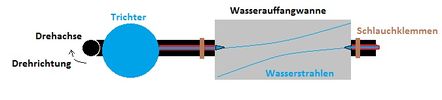
Die Kamera beobachtet die Szene aus dem drehenden System heraus. Wird das Drehlager durch den Motor im Uhrzeigersinn gedreht, werden beide Strahlen Ihrer Flugrichtung folgend nach links abgelenkt, wie in der Abbildung 3 schematisch dargestellt und in der ersten Hälfte des Videos erkennbar ist.
Das heißt, dass der Strahl, der radial nach außen zeigt, der Drehrichtung hinterher läuft und der radial nach innen Zeigende der Drehrichtung vorauseilt (vgl. Brai[4] (ohne Jahr), S. 19).
Wird die Drehzahl des Motors und damit des Systems erhöht, beobachtet man eine stärkere Ablenkung der beiden Strahlen in die jeweilige Richtung.
Wird nun das Drehlager durch den Motor gegen den Uhrzeigersinn gedreht, werden beide Strahlen Ihrer Flugrichtung folgend nach rechts abgelenkt. Auch hier läuft der nach außen gerichtete Strahl der Drehrichtung hinterher und der nach innen gerichtete Strahl eilt der Drehrichtung voraus (vgl. Brai[4] (ohne Jahr), S. 19).
Hier beobachtet man ebenfalls eine stärkere Ablenkung der Strahlen, wenn die Drehzahl des Motors erhöht wird.
Auswertung
Da sich beide Wasserstrahlen kurz nach dem Austritt aus den Düsen in radialer Richtung von der Drehachse weg bzw. zur Drehachse hin bewegen, kann die seitliche Ablenkung nicht allein mit der Zentrifugalkraft erklärt werden. Es muss somit eine weitere Scheinkraft eingeführt werden - die Corioliskraft.
Brai erklärt den Betrag der Corioliskraft in der PHYWE-Schriftenreihe wie folgt:
Bewegt sich die beobachtete Masse in radialer Richtung, so treten zwei Effekte auf:
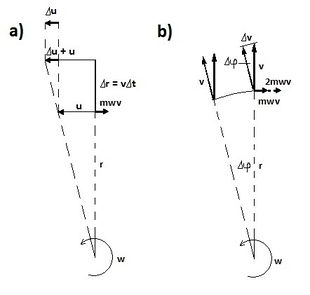
- Während sich die Wasserteilchen bewegen, ändert sich ihr Abstand vom Drehzentrum. In der Zeit legt ein herausgeschnittenes Wasserteilchen den Weg zurück, wobei die Geschwindigkeit des Wasserteilchens ist (vgl. Abb. 4a). Da die Bewegung radial erfolgt, kommt das Wasserteilchen in Bereiche, in denen die Rotation der gesamten Apparatur mit anderer Bahngeschwindigkeit erfolgt, als am Ort der Austrittsöffnung der Düse. Die Rotationsgeschwindigkeit der Apparatur hängt vom jeweils betrachteten Radius und der Winkelgeschwindigkeit gemäß ab. Die Kreisbahngeschwindigkeit des Wasserteilchens an der radialen Position ist also . Wenn es sich um das Stück in radialer Richtung bewegt, gilt:
- ,
- die Geschwindigkeit hat sich um verändert.
- Für eine Geschwindigkeitsänderung ist eine Beschleunigung notwendig:
- Bei der Bewegung des Wasserstrahls radial nach innen, ist die Corioliskraft in Richtung der Drehung gerichtet. Bewegt sich der Wasserstrahl nach außen, ist die daraus folgende Trägheitskraft entgegen der Drehung gerichtet.
- Wenn sich die Apparatur in der Zeit um den Winkel weitergedreht hat, besitzt die Geschwindigkeit nicht mehr radiale Richtung (vgl. Abb 4b). Auch der Geschwindigkeitsvektor muss sich um den Winkel drehen, dies entspricht ebenfalls einer Geschwindigkeitsänderung, d.h. ein weiterer Beschleunigungsanteil wird wirksam. Die Geschwindigkeitsänderung ergibt sich zu , wenn kleine Winkel auftreten und durch Kreisbögen genähert wird. Die auftretende Beschleunigung hat die Größe
- .
Die gesamte auftretende Trägheitskraft setzt sich aus beiden Beschleunigungen zusammen, die dieselbe Größe und Richtung haben. Die Gleichung der Corioliskraft lautet damit
.
Mit zunehmender Winkelgeschwindigkeit bzw. Geschwindigkeit des Wasserstrahls nimmt die Corioliskraft und damit die Ablenkung des Wasserstrahls zu.
(vgl. Brai[4] (ohne Jahr), S. 19f).
Sicherheitshinweise
Vor jedem Einschalten des Motors ist darauf zu achten, dass alle Stativstangen und Teile im drehenden System fest miteinander verbunden sind.
Literatur
- ↑ Popper K.R. (1976): Logik der Forschung; J.C.B. Mohr, Tübingen (Zitiert aus Kircher E./ Girwidz R./ Häußler P. (2000): Physikdidaktik - Eine Einführung in die Theorie und Praxis, S.137; Verlag Vieweg, Braunschweig/Wiesbaden)
- ↑ Kircher E./ Girwidz R./ Häußler P. (2000): Physikdidaktik - Eine Einführung in die Theorie und Praxis; Verlag Vieweg, Braunschweig/Wiesbaden)
- ↑ Haspas K. (1969): Methodik des Physikunterrichts; 2. Auflage, Volk und Wissen Volkseigener Verlag, Berlin)
- ↑ 4,0 4,1 4,2 Brai M. (ohne Jahr): Versuchseinheiten Physik - Rotationsbewegungen, PHYWE-Schriftenreihe, Göttingen)
Siehe auch
Bestimmung der Zentrifugalkraft im beschleunigten Bezugssystem