Bestimmung der Zentrifugalkraft im beschleunigten Bezugssystem
| Bestimmung der Zentrifugalkraft im beschleunigten Bezugssystem | |
 Titelbild: Aufbau zur Analyse der Zentrifugalkraft | |
| Kurzbeschreibung | |
|---|---|
| Die Einführung der Zentrifugalkraft soll anhand der Beobachtungen in zwei Bezugssystemen verdeutlicht werden. Hinzu kommt eine quantitative Analyse. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 9, Klasse 10, Sek. II |
| Basiskonzept: | Wechselwirkung, System |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, Schülerdemoexperiment (nur Sek. II) |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Marek Mandel |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Tobias Ludwig |
Bei der Zentrifugalkraft handelt es sich um eine sogenannte Scheinkraft, die nur in rotierenden und damit beschleunigten Bezugssystemen auftritt. Da es sich bei einem beschleunigten Bezugssystem nicht um ein Inertialsystem handelt, wird zur Erhaltung des ersten Newtonschen Axioms (Trägheitsprinzip) eine Scheinkraft eingeführt, die zu der zur Beschleunigung beitragenden Kraft entgegengesetzt gerichtet ist. Die Zentrifugalkraft wirkt folglich in entgegengesetzter Richtung zur Zentripetalkraft und hat den gleichen Betrag. Berechnen lässt sie sich nach
mit der Masse des Probekörpers, dem Abstand des Probekörpers von der Drehachse (gemessen im rotierenden Bezugssystem) und der Winkelgeschwindigkeit der Rotation.
Das in diesem Beitrag beschriebene Experiment ermöglicht es zunächst, den Schülern qualitativ die notwendige Einführung einer Scheinkraft zum Erhalt des Trägheitsprinzips im rotierendem Bezugssystem aufzuzeigen. Weiterhin können die Abhängigkeiten der (speziell bei der Rotation eingeführten) Zentrifugalkraft quantitativ herausgearbeitet werden.
Inhaltsverzeichnis
Didaktischer Teil
Vielen Schüler steht bei der Einführung der Zentripetalkraft im Unterricht deren Wirkung im Widerspruch zu ihren eigenen Alltagserfahrungen: Bei Kurvenfahrten im Auto oder in der Bahn verspüren sie die Wirkung einer nach außen gerichteten Kraft, in einer Waschmaschine wird die Wäsche an die Trommel gedrückt. Das Problem ist dabei die Argumentation aus zwei unterschiedlichen Bezugssystemen, von denen eines kein Inertialsystem ist. Im Unterricht wird die Zentrifugalkraft als Ursache für die Kreisbewegung eingeführt, ohne jedoch genauer auf den Standpunkt des Beobachters einzugehen. Viele Schüler verbinden mit dem Kraftbegriff eine "fühlbare" physikalische Größe: Wenn jemand an mir zieht, spüre ich die von ihm aufgewandte Kraft. Diese Tatsache übertragen sie auf die besprochene Kreisbewegung, wodurch der Widerspruch entsteht. Der Wechsel des Bezugssystems wurde folglich nicht beachtet. Dieses Problem kann durch den zuvor beschriebenen Versuch angegangen werden. Da es für die meisten Schüler schwierig ist, zwischen beiden Bezugssystemen gedanklich zu wechseln, kann mit Hilfe der Kameraaufzeichnungen das Experiment mehrmals wiederholt und in jedem System separat analysiert werden. Wichtig ist dabei, in jedem System genau zu beschreiben, was beobachtet wurde und wie dies physikalisch zu deuten ist.
Es empfiehlt sich, den Versuch zuerst qualitativ auszuwerten. Dazu betrachte man als erstes die Aufzeichnungen der Kamera im Inertialsystem. Hieran lässt sich das bereits vorhandene Wissen zur Rotation anwenden. Anschließend vergleicht man die Aufzeichnungen mit denen der mitrotierten Kamera. Man beachte die bei der qualitativen Auswertung getroffenen physikalischen Deutungen und ihre Schlussfolgerungen. Eine Gefahr in der Argumentationskette stellt dabei das dritte Newtonsche Axiom (Wechselwirkungsprinzip) dar. Im Inertialsystem ist es noch einfach nachzuvollziehen. Im beschleunigten Bezugssystem wird das Prinzip eingesetzt, um die Zentrifugalkraft auf den Probekörper als Reaktion auf die Rückstellkraft der Feder zu deuten. Die Schüler könnten dagegen die Zentrifugalkraft als Reaktion zur Zentripetalkraft deuten. Allerdings greifen beide Kräfte nur an einem Körper an, wohingegen sich das Wechselwirkungsprinzip auf zwei Körper bezieht. Es ist demnach wichtig, die Auswertung schrittweise vorzunehmen und fachlich sauber zu argumentieren. Nur so gelingt es, den Schülern die Einführung der Scheinkraft zu begründen und mit ihnen das bereits vorhandene Wissen zur Newtonschen Mechanik zu festigen. Weiterhin sollte erwähnt werden, dass neben der Zentripetalkraft auch die Gewichtskraft wirkt, sie allerdings zur Vereinfachung nicht mitberücksichtigt wird. Den Schülern soll bewusst werden, dass zur Beschreibung von Bewegungen der Standpunkt des Beobachters von großer Bedeutung ist.
Die Frage, von welchen Größen die eingeführte Scheinkraft abhängt, sollte bei der quantitativen Auswertung beantwortet werden. Am Ende erhalten die Schüler die ihnen bereits bekannte Formel für die Zentripetalkraft. Diese Erkenntnis deckt sich mit der Beobachtung des ruhenden Körpers im rotierenden Bezugssystem und den in der qualitativen Auswertung getroffenen Schlussfolgerungen. Folglich muss die Zentrifugalkraft vom Betrag her gleich groß wie die Zentripetalkraft sein.
Als Fazit sollte die einfachere Deutung aus dem Inertialsystem hervorgehoben werden. Das anfangs erwähnte Problem der "gefühlten" Kraft kann gelöst werden: Bei einer Kurvenfahrt drückt uns der Autositz mit der Zentripetalkraft auch in die Kurve. Aufgrund unserer Massenträgheit widersetzen wir uns aber der Änderung unserer momentanen Geschwindigkeit. Wir wollen eigentlich weiter geradeaus fahren. Diesen Widerstand "spüren" wir.
Im Anschluss an den Versuch kann über die Anwendung der Zentrifugalkraft (Zentrifugen, Schwerelosigkeit im erdnahen Orbit etc.) gesprochen werden.
Versuchsanleitung
Aufbau
Es werden folgende Materialien für das Experiment benötigt:
- Drehtisch
- Motor mit regulierbarer Drehzahl
- Antriebsriemen, Getriebe oder Ähnliches zur Übertragung des Drehmoments
- verschiedene Massestücke
- Experimentierwagen
- Federkraftmesser
- Muffe oder entsprechend andere Halterung für Federkraftmesser
- Faden
- Längenskala zur Abstandsmessung
- 2 Kameras, davon mindestens eine mit drahtloser Übertragung
- Empfangsgeräte für die Kamerasignale (z.B. ein PC)
- Stoppuhr
- Stativmaterial
optional:
- längliche Holzplatte bei zu kleiner Drehtischoberfläche
- Plexiglasscheibe als Schutzwand vor herausgeschleuderten Teilen
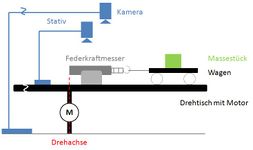
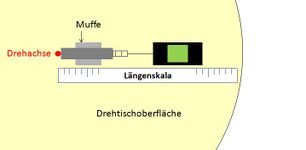
Der Aufbau erfolgt gemäß den beiden dargestellten Abbildungen 1 und 2. Hierfür wird zuerst der Motor mit dem Drehtisch durch den Antriebsriemen oder das Getriebe verbunden. Der Experimentierwagen wird mit Massestücken beladen und durch den Faden mit dem Federkraftmesser verbunden. Der Federkraftmesser wird nun in die Muffe eingespannt. Anschließend wird die gesamte Anordnung auf den Drehtisch gelegt, wobei die Muffe fest mit dem Drehtisch verbunden wird (beispielsweise durch ankleben). Hierbei ist darauf zu achten, dass die Drehachse nicht durch den Federkraftmesser verläuft. Am besten wird das Ende des Federkraftmessers genau an die Drehachse gelegt, eine Begründung für dieses Vorgehen wird im Kapitel Ergänzungen und mögliche Versuchsabwandlungen gegeben. Parallel zu Federkraftmesser, Faden und Experimentierwagen wird nun die Längenskala auf dem Drehtisch befestigt.
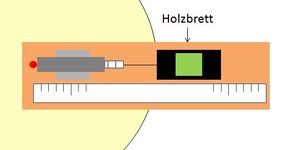
Steht nur ein kleiner Drehtisch zur Verfügung, so kann als Verlängerung die Holzplatte verwendet werden (siehe Abbildungen 3 und 4). Sie ist wiederum fest mit dem Drehtisch zu verbinden.
Abschließend wird das Kamerasystem aus Abbildung 1 installiert: Die drahtlose Kamera wird durch das Stativmaterial auf den Drehtisch montiert. Sie ist dabei so auszurichten, dass sie den Federkraftmesser mitsamt dem Wagen aufzeichnen kann. Sie befindet sich folglich im beschleunigten Bezugssystem. Die zweite Kamera wird mit Stativmaterial außerhalb des Drehtisches angebracht und soll während des Versuches seine gesamte Oberfläche erfassen. Sie befindet sich demnach im ruhenden Bezugssystem (Inertialsystem). Abschließend werden beide Kameras an einem PC angeschlossen bzw. registriert.
Sicherheitshinweise
Es sollte vor Beginn jeder Messung darauf geachtet werden, dass der Federkraftmesser, das Kamerastativ und gegebenenfalls die Holzplatte fest mit dem Drehtisch verbunden sind. Wurde die Verbindung mit Kleber oder doppelseitigem Klebeband realisiert, so ist eine zusätzliche Beschwerung durch Massestücke ratsam.
Man beachte stets: Alle auf dem Drehtisch befindlichen Materialien sind der Zentrifugalkraft unterworfen!
Die Drehzahl des Motors sollte deswegen nur langsam erhöht werden. Durch die Verwendung eines Getriebes kann man sich zusätzlich vor zu hohen Drehzahlen schützen. Weiterhin sollte der Versuchsdurchführende zu jeder Zeit in der Lage sein, den Versuch abzubrechen, indem er den Motor stromlos schalten kann. Als Schülerdemonstrationsexperiment eignet sich der Versuch deshalb nur in der Sekundarstufe II.
Als zusätzlichen Schutz der Schüler vor herausgeschleuderten Teilen kann optional vor dem Experiment eine Plexiglasscheibe aufgestellt werden (siehe Titelbild).
Durchführung
Der Versuch kann nun in zwei Schritten durchgeführt werden:
- In der qualitativen Untersuchung soll die Wirkung der Zentrifugalkraft im rotierenden Bezugssystem verdeutlicht werden. Dafür werden die Aufzeichnungen beider Kameras zeitgleich am PC überwacht, um somit jederzeit zwischen den beiden Bezugssystemen wechseln zu können. Die verwendeten Parameter sind für diesen Versuchsteil uninteressant.
- Es soll nun quantitativ die Abhängigkeit der Zentrifugalkraft untersucht werden. Um die Werte am Kraftmesser möglichst genau ablesen zu können, empfiehlt es sich hierbei, die mitbewegte Kamera nur noch auf den Federkraftmesser zu fokussieren. Man beachte, dass die Werte nur mit Hilfe der mitrotierenden Kamera abgelesen werden können und nicht mit der äußeren.
Im Folgenden wird bei konstanten Parametern jeweils eine Variable verändert.- Durch zusätzliches Beladen des Wagens mit verschiedenen Massestücken kann dessen Gesamtmasse erhöht werden. Zur Bestimmung der exakten Masse kann zur Kontrolle eine Waage herangezogen werden.
- Wird die Fadenlänge vergrößert, so entfernt sich der Wagen auch weiter von der Drehachse. Der jeweilige Abstand kann an der Skala abgelesen werden.
- Eine Erhöhung der Motordrehzahl führt zu einer Vergrößerung der Winkelgeschwindigkeit des Drehtisches. Mit Hilfe der Stoppuhr kann für Umdrehungen die Zeit gemessen werden. Die Winkelgeschwindigkeit berechnet sich nach .
Messunsicherheiten
Quantifizierbare Messunsicherheiten
Für die Messunsicherheit der Masse kann allgemein verwendet werden. Wird eine Waage zur Bestimmung der Masse benutzt, so sind die Angaben des Herstellers zu bevorzugen.
Da es sich beim Experimentierwagen um keine Punktmasse handelt, sollte die Messunsicherheit des Abstandes zur Drehachse großzügig mit gewählt werden.
Allgemein kann für die Messunsicherheit der Zeit angenommen werden, sonst sind die Herstellerangaben der Stoppuhr vorrangig. Entsprechend der Gaußschen Fehlerfortpflanzung ergibt sich die Unsicherheit der Winkelgeschwindigkeit aus .
Die Unsicherheit der Zentrifugalkraft lässt sich nun ebenfalls mit der Gaußschen Fehlerfortpflanzung bestimmen. Es muss jedoch berücksichtigt werden, dass die Feder des Kraftmessers ebenfalls eine zu überwindende Trägheit besitzt. Bei niedrigen Drehzahlen ist die wirkende Zentrifugalkraft jedoch nur sehr gering. Es empfiehlt sich stattdessen eine werteabhängige Messunsicherheit zu verwenden. Hier eine mögliche Regelung:
- Im Bereich gilt für eine Skalenlänge.
- Im Bereich gilt für eine halbe Skalenlänge.
Nicht-quantifizierbare Messunsicherheiten
Die horizontale Lage der Drehtischoberfläche ist nur schwer zu garantieren. Mit Hilfe einer Wasserwaage kann diese Unsicherheit jedoch so gering wie möglich gehalten werden. Je nach Bauart des Motors kann seine Drehzahl kurzzeitig variieren. Hierfür genügt jedoch die zuvor betrachtete Unsicherheit der Winkelgeschwindigkeit. Während der Rotationsbewegung dehnt sich die Feder im Kraftmesser aufgrund der wirkenden Zentrifugalkraft, wodurch sich der Abstand des Experimentierwagens zur Drehachse geringfügig vergrößert. Auch sein Trägheitsmoment wird nicht mitberücksichtigt.
Ergebnisse
Bei den folgenden beiden Videoaufzeichnungen ist der Federkraftmesser mittig eingespannt, wodurch er die Drehachse schneidet. Diese Art der Durchführung wird jedoch nicht empfohlen. Die Aufzeichnungen dienen nur der Demonstration des zuvor beschriebenen Sachverhaltes.
| Video 1: Betrachtung im Inertialsystem |
| Video 2: Betrachtung im rotierenden Bezugssystem |
Betrachtet man den Versuch aus dem Inertialsystem (äußere Kamera, siehe Video 1), so erkennt man, dass der Experimentierwagen aufgrund seiner Verbindung über den Federkraftmesser mit dem Drehtisch dauerhaft auf eine Kreisbahn gezwungen wird. Im rotierenden Bezugssystem (Kamera auf dem Drehtisch, siehe Video 2) entfernt sich der Wagen zur Drehachse nur bei einer Erhöhung der Drehzahl. Bleibt diese hingegen konstant, so verharrt er im Zustand der Ruhe.
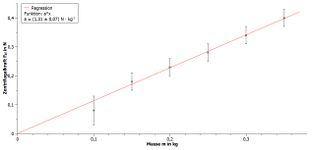
Die gemessenen Werte können nun mit einem Analyse- und Visualisierungsprogramm (im folgenden Beispiel mit QTI-Plot) verarbeitet und der jeweilige funktionale Zusammenhang grafisch dargestellt werden. In den Abbildungen 5, 6 und 7 sind Beispielmessungen mit den entsprechenden Fitkurven dargestellt. Es wurden dabei folgende Parameter gewählt: und . Man beachte, dass alle Fitkurven zwangsweise durch den Ursprung verlaufen müssen. Um bei der Abhängigkeit von einen quadratischen Fit zu vermeiden, wurde hier die Darstellung in Abhängigkeit zu gewählt.
Auswertung
Qualitative Untersuchung
Die Gewichtskraft des Wagens wird im Folgenden zur Vereinfachung nicht mitberücksichtigt. Über den Faden und Federkraftmesser ist der Experimentierwagen mit dem Drehtisch verbunden. Die im Inertialsystem beobachtete Rotation des Wagens resultiert aus der auf den Wagen wirkenden Zentripetalkraft. Aufgrund des Wechselwirkungsprinzips (drittes Netwonsches Axiom) wird die Feder im Kraftmesser als Reaktion auf die Zentripetalkraft gespannt. Folglich kann am Federkraftmesser der Betrag der wirkenden Zentripetalkraft abgelesen werden (vgl. Demtröder[1] (2008), S. 54f).
Im rotierenden Bezugsystem befindet sich der Wagen bei konstanter Winkelgeschwindigkeit in Ruhe. Da die Feder des Kraftmessers gespannt ist, muss auf den Wagen eine Rückstellkraft wirken. Im Zustand der Ruhe muss jedoch die Summe aller wirkenden Kräfte null sein (als Resultat aus dem Trägheitsprinzip). Würde dieses Prinzip hier nicht mehr gelten, so würde folglich auch das zweite Newtonsche Axiom (die Kraft entspricht der zeitlichen Änderung des Impulses) keine Gültigkeit mehr besitzen. Der Wagen könnte demnach nicht mehr als träge Masse angesehen werden. Um dieses Problem zu umgehen, führt man eine Scheinkraft ein, die sogenannte Zentrifugalkraft. Sie wirkt entgegen der Rückstellkraft der Feder und ist vom Betrag her gleich groß. Da am Federkraftmesser der Betrag der Rückstellkraft ablesbar ist, entspricht dieser Wert gleichzeitig dem Betrag der Zentrifugalkraft. Eine Scheinkraft kann demnach im beschleunigten Bezugssystem auch gemessen werden (vgl. Demtröder[1] (2008), S. 88f). Man beachte, dass die Ursache für das Spannen der Feder noch nicht geklärt wurde. Filmt die mitbewegte Kamera nur den Drehtisch und nicht die Umgebung, so kann keine Ursache für diese Spannung festgestellt werden. Man kann nur aufgrund der Zentrifugalkraft Rückschlüsse auf die Bewegung des Drehtisches ziehen. Wird zusätzlich auch die als rotierend wahrnehmende Umgebung von der Kamera mit aufgezeichnet, so kann die Spannung der Feder sofort durch das Wechselwirkungsprinzip wie zuvor beschrieben auf die Zentripetalkraft zurückgeführt werden (vgl. Dreyer[2] (2002), S. 78f).
Quantitative Untersuchung
Anhand der Fitkurven aus den Abbildungen 5, 6 und 7 lässt sich die folgern: . Aus diesen Proportionaliäten ergibt sich mit der Einführung einer Korrekturkonstante folgender Zusammenhang:
Abschließend soll diese Konstante aus dem Quotienten vom Anstieg der Fitfunktion und dem Produkt der konstanten Parameter bestimmt werden:
Ihre Unsicherheit berechnet sich wiederum mit der Gaußschen Fehlerfortpflanzung. In Tabelle 1 wurde die Konstante für die Beispielmessungen aus den Abbildungen 4, 5 und 6 bestimmt.
| Abhängigkeit von |
Parameter | Anstieg der Fitfunktion | Produkt der Parameter | Korrekturkonstante |
|---|---|---|---|---|
Es folgt, dass ist. Als Resultat erhält man die Formel zur Berechnung des Betrages der Zentrifugalkraft, wenn die Vektoren der Winkelgeschwindigkeit und des Abstands senkrecht zueinander stehen. Sie lautet:
- .
Ergänzungen und mögliche Versuchsabwandlungen
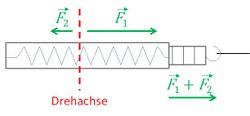
Die Drehachse sollte den Federkraftmesser nicht in zwei Hälften teilen. Wie in Abbildung 8 zu erkennen ist, greift aufgrund der Trägheit des Experimentierwagens auf der einen Seite des Kraftmessers die Zentrifugalkraft an. Da die Feder jedoch selbst eine Trägheit besitzt, wirkt auf den Federabschnitt im anderen Teil des Kraftmessers ebenfalls eine Zentrifugalkraft (im Bild ). Effektiv kann damit am Federkraftmesser nur die Summe beider Kräfte abgelesen werden. Bei einem späteren Fit der Messwerte kann folglich keine Proportionalität festgestellt werden.
Viele Schulen verfügen über ein Radialkraftmessgerät. Dabei wird der Federkraftmesser in der Drehachse positioniert und der Faden mit Hilfe einer Umlenkrolle zum Experimentierwagen geführt (siehe [1] Fachbereich Physik des Hohenstaufen-Gymnasiums Kaiserslautern). Neuere Versionen dieses Versuches verzichten sogar auf den Federkraftmesser (vgl. [2] PHYWE). Nachteilig an diesen Versuchen ist einerseits die Tatsache, dass die Messung nicht mehr innerhalb der Bewegungsebene stattfindet. Die Installation einer mitbewegten Kamera, die zugleich Wagen und Kraftmesser aufzeichnet, wird damit erschwert. Zudem kommt durch die feste Umlenkrolle eine weiteres Bauteil hinzu, auf das zuvor eingegangen werden muss. Das angestrebte Ziel, den Schülern den Wechsel zwischen den Bezugssystemen zu erleichtern, ist somit schwer umsetzbar. Andererseits leidet beim Verzicht auf den Federkraftmesser die Anschaubarkeit der Kraftwirkung im rotierenden Bezugssystem.
Anstelle der Winkelgeschwindigkeit kann auch die Abhängigkeit zur Bahngeschwindigkeit des Experimentierwagens betrachtet werden, da zu dieser Größe die Schüler möglicherweise einen besseren Zugang finden. Man beachte dabei jedoch, dass gilt. Damit folgt für die Zentrifugalkraft:
Bei konstanter Bahngeschwindigkeit besteht also zwischen der Zentrifugalkraft und dem Abstand zur Drehachse ein antiproportionaler Zusammenhang. Dieser Sachverhalt sollte nach der Versuchsauswertung besprochen werden.
Literatur
- ↑ 1,0 1,1 Demtröder, W. (2008): Experimentalphysik 1 - Mechanik und Wärme; 5. Auflage, Springer-Verlag, Berlin
- ↑ Dreyer, H. P. (2002): Kreisbewegung - Ein Leitprogramm zur Mechanik; ETH Zürich, verfügbar unter ETH Zürich [10.09.2013]
Siehe auch
- Fachbereich Physik des Hohenstaufen-Gymnasiums Kaiserslautern: http://www.hsg-kl.de/faecher/ph/versuche/mechanik/kreisbewegung2.php [10.09.2013]
- PHYWE: http://www.phywe.de/51/pid/29416/Zentripetalkraft-.htm [10.09.2013]