Wasserthermometer
| Wasserthermometer | |
 Abb.1: Aufbau des Wasserthermometers | |
| Kurzbeschreibung | |
|---|---|
| Funktionsweise und Grenzen eines Wasserthermometers | |
| Kategorien | |
| Thermodynamik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klassen 7,8 |
| Basiskonzept: | System, Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | {{{AnzahlExp}}} |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Karl Krum |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Das Thermometer ist nicht nur ein überall und dauernd benutzter Alltagsgegenstand, sondern hat auch die Forschung auf dem Gebiet der Thermodynamik erst ermöglicht.
Das Experiment beschäftigt sich mit dem Aufbau und der Eichung eines Wasserthermometers vor einem historischen Hintergrund.
Wie kann man erreichen, dass zwei verschiedene Thermometer bei der gleichen Temperatur auch den gleichen Wert anzeigen?
Warum wird in Flüssigkeitsthermometern gefährliches Quecksilber benutzt und nicht einfaches Wasser?
In den Ergebnissen sieht man den Effekt des nicht-linearen Ausdehnungskoeffizienten von Wasser, weswegen es nicht für Thermometer im alltäglichen Messbereich geeignet ist.
Inhaltsverzeichnis
Didaktischer Teil
Dieses Experiment hat in erster Linie einen historischen Schwerpunkt. Die Lehrperson kann mit den Schülerinnen und Schülern schrittweise die historische Entwicklung des Thermometers und der heute benutzten Messskalen nachvollziehen und gleichzeitig die Bedeutung des Thermometers für die Thermodynamik und die Formulierung des Energieerhaltungssatzes herausarbeiten. In diesem Zusammenhang kann die Schülerfrage auftreten, warum in Flüssigkeitsthermometern nicht einfach Wasser benutzt wird, statt Quecksilber (Wenn nicht, schafft man es als Lehrer die Frage zu "induzieren"). Darauf geht der zweite Teil des Experimentes ein.
Dass Luft sich bei Erwärmung ausdehnt, war schon in der Antike bekannt. Doch erst im 17. Jhd. wurden Thermometer, wie man sie heute kennt und benutzt, gebaut. Anfang des 18. Jhd. wurden Temperaturskalen festgelegt (Celsius, Fahrenheit, Kelvin), die eine reproduzierbare Eichung von Thermometern ermöglichten. Damit wurde ein Instrument geschaffen, mit dem physikalisch gearbeitet werden konnte.
Hier können die Schülerinnen und Schüler nachvollziehen, dass z.B. die Fixpunkte der Celsius-Skala aus praktischen Gründen so gewählt wurden. Eiswasser und kochendes Wasser sind die einfachsten Möglichkeiten eine fixe Temperatur zu erzeugen.
Schon im Mittelalter war bekannt, dass man die Intensität und die Quantität einer Wärme unterscheiden muss. Diese Größen sind heute als Temperatur und Wärmemenge bekannt. Es gab Theorien über den Wärmeaustausch, die Temperaturangleichung und die Energieerhaltung, die alle schwer zu bestätigen waren.
Schwer widerlegbare Fehlvorstellungen waren z.B.:
- Wärmegleichgewicht ist Wärmegleichheit
- die Wärmemenge eines Körpers hängt nur vom Volumen und der Masse ab
- die Kinetische Energie, die bei Reibung verloren geht, widerlegt die Energieerhaltung
Diese Dinge - und noch mehr - sind heute mit relativ einfachen Experimenten widerlegbar. Die Grundvorraussetzung für alle ist aber eine unabhängige Messung einer Temperatur mit einem Thermometer. An diesem Punkt sieht man klar die historische Bedeutung, die eine Behandlung im Unterricht rechtfertigt.
Besonders schön ist die historische Bedeutung in Simonyi (2001), [1] S.355-358 nachzulesen.
In diesem Gedankengang, und nachdem man selber ein funktionierendes Thermometer mit Wasser gebaut und geeicht hat, bietet sich die Frage an, warum giftiges Quecksilber benutzt wird und nicht einfaches Wasser. Hier kann man mit dem selbstgebauten Thermometer einmal die Raumtemperatur messen lassen und wird einen klar falschen Wert bekommen (ca. 15°C). Will man diesen Aspekt ausführlicher beleuchten, schließt sich dann der zweite Teil des Experiments an, mit dem man den nicht-linearen Ausdehnungskoeffizienten von Wasser qualitativ nachvollziehen kann (s. Auswertung).
Physikalische Grundlagen
Alle Stoffe verändern ihr Volumen bei Temperaturänderung. Wichtig ist dabei der stoffspezifische Ausdehnungskoeffizient . Dieser ist meist konstant, kann aber von der Temperatur abhängen. Dies ist bei Wasser der Fall, was die Voraussetzung für den zweiten Teil des Experiments ist. Außerdem fließen die Temperaturänderung und das Ausgangsvolumen linear ein. Die Volumenänderung ergibt sich damit zu:
Die Anomalie des Wassers sorgt dafür, dass Wasser bei 4°C die größte Dichte hat. Dementsprechend verringert sich das Volumen von 0°C bis 4°C, der Ausdehnungskoeffizient ist also negativ. Über 4°C nimmt er immer schneller zu. Er ist also vorallem bei Temperaturen im Bereich von 0°C bis 30°C sehr nicht-linear, was sich in den Ergebnissen niederschlägt. Viele andere Stoffe, so z.B. Alkohol und Quecksilber haben in den relevanten Temperaturbereichen sehr konstante Ausdehnungskoeffizienten, was sie für Thermometer sehr gut benutzbar macht. Schön zu sehen ist der Effekt in dieser Grafik: Ausdehnungskoeffizienten verschiedener Stoffe.
Weiterhin ist relevant, dass Stoffe eine konstante Temperatur behalten, während ein Aggregatszustandsübergang stattfindet. Kochendes Wasser, dem man weite Hitze zuführt, befindet sich konstant und sehr genau an seinem jeweiligen Siedepunkt (vom Luftdruck abhängig), da jede zugeführte Energie benötigt wird um Wasser zu verdampfen und somit die Temperatur nicht erhöht wird. Analog hat Eiswasser, das langsam schmilzt konstant 0°C. Dadurch werden für den ersten Teil die Fixpunkte geschaffen, an denen man das Thermometer eichen kann.
Versuchsanleitung
Aufbau
Folgende Dinge werden benötigt:
- Becherglas: 1 Liter
- Erlenmeyerkolben: 600ml
- Glasrohr: Innendurchmesser: 6mm, Länge: 65cm
- Stopfen für Kolben, mit Loch für Glasrohr
- Stativ mit Halterung für den Kolben
- elektrische Heizplatte
- elektrisches Thermometer
- Wasser mit roter Lebensmittelfarbe im Kolben/Rohr
- Wasser klar als Wasserbad im Becherglas
- Eis für Eiswasser
- Zollstock
Den Kolben befestigt man am Stativ und hängt ihn möglichst vollständig in das Becherglas. Dieses wird mit Wasser befüllt, welches als Wasserbad dient. Mit dem elektrischen Thermometer misst man die Temperatur im Inneren des Kolbens. Dies war mir nicht möglich, da ich keinen passenden Stopfen hatte. Deshalb habe ich die Temperatur im Wasserbad gemessen.
Das Becherglas steht auf dem Tisch, nur zum Erhitzen des Wasserbades stellt man es direkt auf die Heizplatte (Becherglas muss hitzefest sein). Alternativ kann man auch einen Bunsenbrenner nehmen, muss dann aber alles entsprechend höher anbringen.
Den Kolben füllt man mit dem farbigen Wasser, sodass das Rohr zu ca. 1/4 gefüllt ist. Dann sollte es auch bei 100°C nicht überlaufen. Die von mir benutzten Größen sind nur ein Richtwert und können abhängig von den verfügbaren Materialien anders gewählt werden.
Durchführung
Im ersten Teil müssen beide Fixpunkte erreicht werden. Es hat sich als sinnvoll gezeigt, erst das Eiswasser anzusetzen. Man hängt den Kolben in das Becherglas und füllt mit Eisstücken und möglichst kaltem Wasser auf. Um das thermische Gleichgewicht zu erreichen, sollte es ca. 15-20 Minuten stehen. Falls fast alles Eis schmelzen sollte, muss das Wärmebad mit mehr Eis ausgetauscht werden. Das Bad kann man parallel mit dem elektrischen Thermometer beobachten. Man sollte regelmäßig die Höhe der Wassersäule messen. Wenn diese sich nicht mehr wirklich verändert, kann man den Wert als Eichung bei 0°C nehmen.
Dann wird das Eiswasser entfernt, das Becherglas auf die Heizplatte gestellt und mit kochendem Wasser (z.B. aus einem Wasserkocher) aufgefüllt. Dann wird die Heizplatte angeschaltet, das Wasser zum Kochen gebracht und wieder gewartet bis sich das thermische Gleichgewicht einstellt. Anschließend wird wieder die Höhe gemessen und als Eichpunkt bei 100°C genommen.
Nun kann aus den beiden Werten eine Eichgerade bestimmt werden, mit der man für eine beliebige gemessene Höhe eine dazugehörige Temperatur erhält. Hier ist es wichtig zu wissen, wie weit die Schülerinnen und Schüler im Mathematik Unterricht mit linearen Zusammenhängen und Geradengleichungen sind. Davon hängt es ab, ob sie in der Lage sind, diese Formel selbst zu ermitteln.
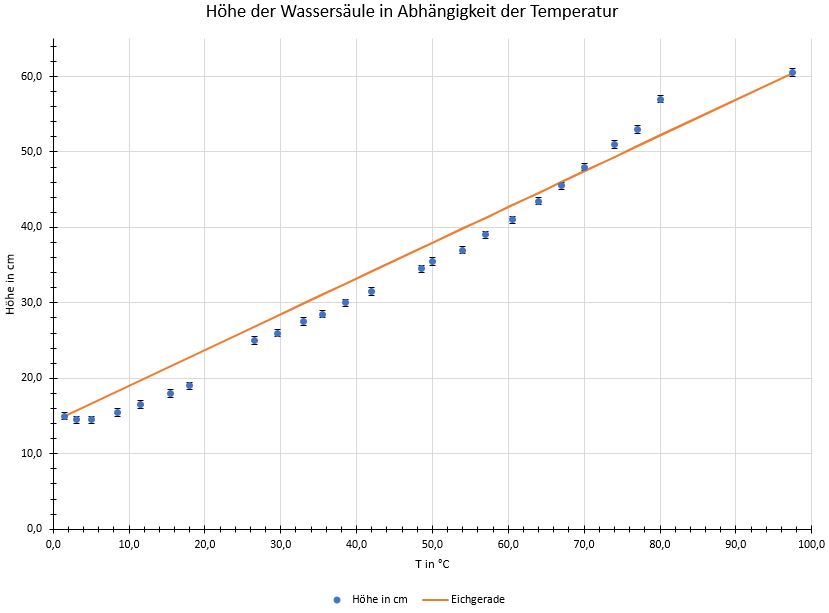
Im zweiten Teil wird das Wasserbad wieder jeweils zu beiden Fixpunkten gebracht. Anschließend lässt man es abkühlen bzw. sich erwärmen bis es sich der Raumtemperatur nähert. Das kann durchaus durch Beimischung von Leitungswasser beschleunigt werden, man muss nur jedesmal das thermische Gleichgewicht abwarten. Währenddessen werden immer wieder Temperatur und Höhe der Säule aufgeschrieben. Aus diesen zwei Messungen (von unten und von oben zur Raumtemperatur) ergibt sich ein Diagramm (s. Abb.2).
Ergebnisse und Auswertung
Im ersten Teil erhält man zwei Werte, durch die eine Eichgerade gelegt wird. Als Ablesefehler habe ich angesetzt. Dieser ist aber relativ aussagelos, da systematische Fehler stark überwiegen. Es ist nicht nachzuprüfen, wie gut das thermische Gleichgewicht erreicht wurde. Außerdem habe ich es auch bei langem Kochen nie geschafft, dass das elektronische Thermometer mehr als 98°C im Wasserbad anzeigt. Ich weiß nicht, ob das ein Fehler des Thermometers ist, oder ob ein nicht berücksichtigter Faktor das Erreichen von 100°C verhindert.
Wasserverdunstung sollte keinen merklichen Einfluss haben, da das Rohr mit 6mm recht dünn ist.
Als Eichpunkte habe ich folgende erhalten:
| Fixpunkt | Wasserbad | Höhe |
|---|---|---|
| 0°C | 1,5°C | 15cm |
| 100°C | 97,5°C | 60,5cm |
Daraus ergibt sich eine Eichgerade, mit der man eine gemessene Höhe in eine Temperatur umrechnen kann (s. Abb.2):
Bei einer gemessenen Raumtemperatur von 22°C hat die Säule im Thermometer eine Höhe von 23cm. Mit obiger Eichung ergibt sich eine Temperatur von 17,6°C, was mit 20% deutlich unter dem wirklichen Wert liegt. Dies ist allerdings kein Indiz für eine schlechte Messung, sondern genau das, was man durch den nicht linearen Ausdehnungskoeffizienten erwartet.
Hier könnte man als Lehrperson diese Erklärung bringen und das Experiment beenden. Oder man führt den zweiten Teil des Experimentes durch, um diesen Effekt stärker zu beleuchten.
Aus den beiden Messungen im zweiten Teil ergeben sich viele Messpunkte, die man zusammen mit der vorher ermittelten Eichgeraden in ein Diagramm einträgt (s. Abb.2). Die Messdaten sind in Tab.2 zu finden.
Man kann an dem Diagramm schön erkennen, wie sich die Höhe von 0°C bis ca. 10°C nicht wirklich verändert. In diesem Bereich ist der Ausdehnungskoeffizient von Wasser erst negativ, und dann nur knapp positiv, was zu kaum Veränderungen führt. Dementsprechend ist die Höhe der Säule deutlich geringer, als bei der Eichgerade angenommen. Da der Koeffizient mit steigender Temperatur immer größer wird, steigt die Höhe immer schneller. Der Koeffizient ist der Anstieg der Höhe, also quasi die Ableitung. Deswegen sieht die Kurve Parabel ähnlich aus. Die leichte Verschiebung des rechten und linken Teils der Kurve, liegt daran, dass es zwei getrennte Messungen sind, die sich jeweils von oben bzw. unten an die Raumtemperatur annähern.
Ab ca. 70°C liegen die Messwerte über der Eichgeraden. Dies sollte eigentlich nicht der Fall sein. Beim Entfernen der Heizplatte war zu beobachten, dass die Temperatur des Wasserbads sehr schnell auf 80°C gefallen ist, die Säule sich aber nicht mitbewegt hat. Offensichtlich war das thermische Gleichgewicht sehr gestört. Auch längeres Warten hat den Effekt nur bedingt verhindert, auch wenn es sich später wieder eingependelt hat. Idealerweise müssten alle Messwerte von 30°C bis 80°C nach rechts gestreckt sein und würden sich dann nahtlos unter die Eichgerade einfügen. Dieser Effekt ist der größte Fehler der Messung und überschattet die statistische Messabweichung von deutlich. Den Effekt sollte man weitgehend entfernen können, wenn man es schafft die Temperatur direkt im Kolben zu messen, und nicht wie ich im Wasserbad. Ohne diesen Fehler wäre der Verlauf der Ausdehnung von Wasser sehr gut wiedergegeben. Man erkennt so gut das Problem der Temperaturmessung mit Wasser. Mit der Eichgeraden legt man eine Fitfunktion durch zwei Messwerte, deren Annahmen nicht der Realität entsprechen. Entsprechend falsch wären Messungen mit diesem Instrument.
Fazit
Beide Teile des Experiments funktionieren sehr gut und geben zur Theorie passende Ergebnisse. Beim ersten Teil hält sich der Zeitaufwand mit ca. 30-45 Minuten in Grenzen. Die Wartezeit kann gut benutzt werden, um den historischen Kontext des Experiments herauszuarbeiten.
Der zweite Teil gibt zwar ein schönes Ergebnis, allerdings ist zu bemerken, dass in der Praxis der Zeitaufwand wahrscheinlich zu hoch ist, um die Durchführung zu rechtfertigen.
Sicherheitshinweise
Hier ist die Verbrennungsgefahr an der Heizplatte sowie die Verbrühungsgefahr mit heißem Wasser zu beachten. Vorallem wenn das Wasser kocht und man die Heizplatte entfernt, ist darauf zu achten, dass man sehr vorsichtig ist, da alle Glasbehälter und Inhalte kochend heiß sind.
Dies sollte nur unter Aufsicht geschehen, oder von der Lehrperson selbst duchgeführt werden.
Literatur
- ↑ Simonyi, Károly (2001): Kulturgeschichte der Physik: Von den Anfängen bis heute, 3. Auflage; Harri Deutsch-Verlag, Frankfurt am Main
Siehe auch
Anhang
Tabelle 2: Messwerte des zweiten Teils des Experimentes. Die ersten beiden sind die Eichwerte.
| T in °C | Höhe in cm |
| 1,5 | 15,0 |
| 97,5 | 60,5 |
| 80,0 | 57,0 |
| 77,0 | 53,0 |
| 74,0 | 51,0 |
| 70,0 | 48,0 |
| 67,0 | 45,5 |
| 64,0 | 43,5 |
| 60,5 | 41,0 |
| 57,0 | 39,0 |
| 54,0 | 37,0 |
| 50,0 | 35,5 |
| 48,5 | 34,5 |
| 42,0 | 31,5 |
| 38,5 | 30,0 |
| 35,5 | 28,5 |
| 33,0 | 27,5 |
| 29,5 | 26,0 |
| 26,5 | 25,0 |
| 3,0 | 14,5 |
| 5,0 | 14,5 |
| 8,5 | 15,5 |
| 11,5 | 16,5 |
| 15,5 | 18,0 |
| 18,0 | 19,0 |