Pendelwagen
| Pendelwagen | |
 Pendelwagen (mit Platz für Kamera) | |
| Kurzbeschreibung | |
|---|---|
| Der Pendelwagen demonstriert Kräftegleichgewicht in einem beschleunigten Bezugssystem und dient der Motivation des Scheinkraftbegriffs. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. I |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Jordi Kling |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Franz Boczianowski |
Es ist erstaunlich, dass selbst unkompliziert wirkende Reflexionen über den freien Fall einem Giganten wie Einstein zur Entwicklung der allgemeinen Relativitätstheorie verholfen haben. So formulierte dieser rückblickend auf das Jahr 1907 seinen glücklichsten Gedanken (vgl. Körner[1] (1998), S. 218 f.):
"Für einen Beobachter, der sich im freien Fall vom Dach eines Hauses befindet, existiert – zumindest in seiner unmittelbaren Umgebung – kein Gravitationsfeld. Wenn nämlich der fallende Beobachter einige andere Körper fallen läßt, dann befinden sie sich im Bezug auf ihn im Zustand der Ruhe oder gleichförmigen Bewegung."
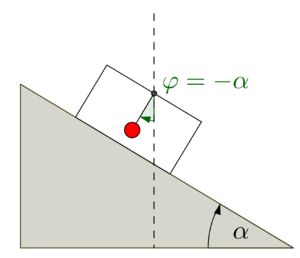
Tatsächlich kann Einsteins glücklichster Gedanke auch als Sonderfall des Pendelwagens aufgefasst werden, dem die folgende Fragestellung zugrunde liegt:
Ein Kasten, in dem sich ein Pendel befindet, rutscht reibungsfrei auf einer schiefen Ebene. Gibt es eine anfängliche Auslenkung des Pendels, die sich nach dem Losrutschen nicht mehr verändert?
Die Beantwortung dieser Frage ist nichttrivial und eignet sich hervorragend dafür, Schülern zu zeigen, dass es durchaus mehrere Interpretationsmöglichkeiten für die Begriffe Ruhe oder Kräftegleichgewicht gibt und welche Rolle der Scheinkraftbegriff dabei spielt.
Inhaltsverzeichnis
Beantwortung der Frage nach der initialen Auslenkung
| Ohne Herleitung (vgl. dafür SMART Board-Notizen[2] des Autors) soll kurz auf die beiden zu unterscheidenden Fälle hingewiesen werden, die im Rahmen der analytischen Mechanik berechnet werden können.
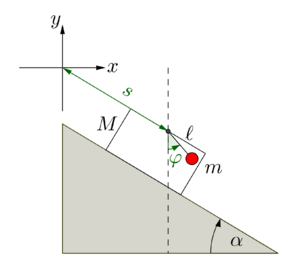
Das System besitzt zwei Freiheitsgrade, man wähle günstigerweise die Verschiebung des Pendelaufhängers entlang der Ebene und die Auslenkung des Pendels zur -Achse als verallgemeinerte Koordinaten. Stellt man mit dem Lagrange-Formalismus die Bewegungsgleichungen auf und setzt die Prämisse darin ein (die initiale Auslenkung soll konstant bleiben und all ihre zeitlichen Ableitungen verschwinden), so kann man die Bedingung ablesen. Die Frage nach der Existenz einer sich nicht mehr verändernden Auslenkung lässt sich bejahen und es ergeben sich zwei mögliche Szenarien:
|
|||||||||||
Didaktische Aspekte
Der Pendelwagen setzt die Pfeildarstellung von Kräften und insbesondere die Orthogonalzerlegung der Gewichts- in die Hangabtriebs- und die Normalkraft an der schiefen Ebene voraus. In den Vortragsfolien[3] zum Artikel sind verschiedene Experimente aufgeführt, die eine induktive Herangehensweise an die Zerlegung von Kräften (ohne Arithmetisierung durch Vektoren) vorstellen.
Dieser Abschnitt dient der Zusammenfassung von Schwierigkeiten, welche die didaktischen Rekonstruktion des Kraftbegriffs charakterisieren. Es wird weiterhin erläutert, inwiefern der Pendelwagen an einige dieser Schwierigkeiten anknüpfen kann und ein sinnstiftendes Experiment für den Mechanikunterricht darstellt.
Didaktische Schwierigkeit des Kraftbegriffs
Der Begriff Kraft als physikalische Grundgröße erstreckt sich über die gesamte Mechanik. Fragt man jedoch Menschen verschiedenen physikalischen Wissensstands (Schüler, Lehrer, Professor) nach einer Definition des Kraftbegriffs, so erhält man keine einheitliche Antwort – stattdessen variieren diese nach Gruppe und individuellen Assoziationen (siehe Vortragsfolien[3], S. 3–4). Befragte Schüler eines Wahlpflichtkurses Informatik der zehnten Klasse scheinen beispielsweise keine greifbare Vorstellung zu haben und erwidern vage formulierte Definitionen ("Kraft ist, wie gut..." oder "Kraft entsteht, wenn...") oder beziehen sich inkorrekt auf andere physikalische Größen ("Kraft ist Energie (pro Zeit)"). Häufig erfolgt auch eine Orientierung am Kraftbegriff in der Alltagssprache (körperliche Kraft, Stichworte "Muskeln, Bizeps, ..."). Im Leistungskurs Physik und im Studium präferiert man die axiomatische Definition oder gleichwertige Formeln (). Die befragten Lehrer und Hochschullehrer bezeichnen eine Kraft als Ursache einer Wirkung (z. B. von Feldern auf Probekörper). Einer von ihnen argumentiert, man könne die Wirkung einer Kraft wahrnehmen – was jedoch eine Kraft ist, wisse niemand.
Die Grundaussage dieses einleitenden Beispiels ist, dass ein fundamentaler Begriff der Physik so abstrakt zu sein scheint, dass er gar keine universelle Definition besitzt. Elementarisierung funktioniert nicht, wenn jeder seine eigene Auffassung eines Lerngegenstands besitzt (vgl. Kircher et al.[4] (2015), S. 110) und das ist das Grundproblem der didaktischen Rekonstruktion. Der Physikdidaktiker fragt sich, wie er seinen Lernenden einen Begriff greifbar machen soll, den er wahrscheinlich selbst nicht versteht (oder verstehen kann). In der Sekundarstufe I zeigt man wenig Verständnis für die axiomatische Herangehensweise und ist viel mehr von körperlichen Erfahrungen geleitet. Begriffe wie Kraft, Arbeit oder Energie sind in der Alltagssprache in etwa synonym (vgl. Kircher et al.[4] (2015), S. 112). Es ist wenig überraschend, dass der Kraftbegriff eine Reihe von Alltagsvorstellungen mit sich bringt (vgl. Wiesner et al.[5] (2015), S. 38 f.), die im Laufe der Begriffsbildung alle berücksichtigt werden sollten (, Kraft ist eine Eigenschaft, Kraft wird verbraucht, ...). Die Vortragsfolien[3] fassen eine Reihe von Experimenten zusammen, die sich an der Einführung des Kraftbegriffs anhand von Alltagserfahrungen orientierten (vgl. Boczianowski[6] (2007)).
Das Problem bei der Begriffsbildung besteht darin, dass die konventionelle, axiomatische Definition der Kraft im schulischen Rahmen undenkbar ist. In der analytischen Mechanik startet man bei der Bahnkurve einer Probemasse und definiert ihre Geschwindigkeit sowie ihre Beschleunigung , wobei diese Größen eine sinnvolle anschauliche Bedeutung besitzen. Das Objekt (welche Schreibweise man auch immer verwenden möchte) nennt der Physiker sodann "Kraft". Was genau man darunter zu verstehen hat, ist eine Frage, die in einem axiomatischen System keine wirkliche Antwort findet.
Für diese Herangehensweise fehlen einerseits jedwede mathematische Vorkenntnisse (die Mathematik ist ein mächtiges Werkzeug und muss gesondert erlernt werden), andererseits ist die Sachstruktur des Unterrichts eine ganz andere als die Fachstruktur der Physik. Bereits bei einer allgegenwärtigen Grundgröße der Mechanik trennt sich die Wissenschaft vom Unterrichtsfach. Der angehende Physikdidaktiker sollte sich der Schwierigkeit bewusst sein, für die Definition des Kraftbegriffs vermutlich keine einheitliche Reduktionsebene zu finden, die den Ansprüchen der Wissenschaft und der Einbindung von Präkonzepten gleichzeitig gerecht wird.
Bezugssysteme und Scheinkräfte
Denkt man an den Physikunterricht zurück, den man in der siebten oder achten Klasse genossen hat, hört man seinen Lehrer womöglich im Gedanken fragen: "Bewegt sich eine Person, die in einem vorbeifahrenden Zug sitzt?" Bejaht ein Schüler die Frage, so lautet die Antwort des Lehrers oder eines Mitschülers, dass die im Zug sitzende Person doch nichts macht und der Kaffee auf dem Tisch vor ihr auch nicht schwappt. Verneint ein Schüler die Frage, kommt entsprechend der Einwand, dass der sich auf dem Bahnhof befindliche der vorbeifahrenden Person hinterherwinken kann. Beide Argumentationen sind legitim, obwohl sie sich widersprechen – die Schüler erfahren einen Konzeptwechsel (vgl. Kircher et al.[4] (2015), S. 666). Die Idee der Unverzichtbarkeit von Bezugssystemen ist gesät und im Basiskonzept System ist diese Einsicht auch curricular vorgesehen (vgl. SenBJS[7] (2006), S. 16).
Das Verständnis des Kraftbegriffs wird durch diese fundamentale Gegebenheit jedoch noch weiter erschwert. Beginnt ein Bezugssystem gegenüber einem räumlich fixierten Bezugssystem mit einer beschleunigten Bewegung seines Koordinatenursprungs oder einer Rotation um irgendeine Achse, verkompliziert das die Betrachtung der wirkenden Kräfte. Der Physiker findet heraus, dass die Gültigkeit des zweiten Newton'schen Axioms
im Allgemeinen gar nicht gegeben ist (sondern lediglich im Inertialsystem gilt) und stattdessen die Form
annimmt, wobei gestrichene Größen die Sicht des gestrichenen Bezugssystems angeben. Diese zusätzlichen Terme nennt man Scheinkräfte, weil sie ausschließlich in Bezugssystemen mit (beschleunigt) oder (rotierend) existieren. Wenn nun bereits der Kraftbegriff per se kaum greifbar für den Lernenden ist, stellt der Scheinkraftbegriff erst recht ein didaktisches Problem dar: Es gibt also auch Kräfte (was auch immer "Kräfte" schon für Abstrakta sein mögen), die manchmal existieren und manchmal nicht – je nachdem, wie man hinschaut.
Das vermutlich allgegenwärtigste Beispiel ist das lenkende Auto, bei dem man nach außen gedrückt wird. Der Schüler spürt diese Wirkung, sie ist körperlich erfahrbar. Die Frage, warum die Zentrifugalkraft als Ursache dieser Wirkung gar nicht zu existieren braucht, ist entsprechend nachvollziehbar. Nach eigener Erfahrung wird der genauen Beantwortung dieser Frage im Schulunterricht kaum nachgegangen, vielmehr ist man bei der Benennung der Kräfte inkonsequent (auch manche Hochschuldozenten verwenden Zentripetalkraft und Zentrifugalkraft synonym, obwohl die subtile Unterscheidung eine sehr wichtige ist: der Unterschied liegt nicht nur im Vorzeichen – ersteres Objekt existiert immer, letzteres nicht). Es verwundert nicht, dass auch die "Dominanz der Zentrifugalkraft" ein gängiges Präkonzept bei Lernenden ist (vgl. Wiesner et al.[5] (2015), S. 39).
Mit dem Pendelwagen kann der Lehrer gut an die Diskussion über eine Bewegung in verschiedenen Bezugssystemen anknüpfen und die Einführung des Scheinkraftbegriffs motivieren. Filmt man das Experiment aus zwei Perspektiven (Kamera am Wagen, Kamera im Raum), kontrastieren beide Aufnahmen gut hinsichtlich der Dynamik des Pendelkörpers bei der Bewegung des Wagens und man kann mit den Schülern eine ergiebige Diskussion darüber führen, welche Kräfte im jeweiligen Bezugssystem wirken müssen, um die entsprechende Bewegung zu erzielen. Es bietet sich eventuell an, statt vom (mitbewegten) Bezugssystem von der (mitbewegten) Kamera zu sprechen. Diese horizontale Reduktionsebene ist vermutlich greifbarer als der abstrakte Systembegriff und es ist nicht abwegig, sich in die Perspektive einer Kamera hineinzudenken. Im Idealfall durchlaufen die Schüler die im Abschnitt Auswertung aufgeführte Gedankenkette und erkennen die Notwendigkeit des Scheinkraftbegriffs als logische Konsequenz ihrer Beobachtung.
Durch die Verwendung von Videoaufnahmen bedarf es keiner Gedankenexperimente (vom Hochhaus springen und gleichzeitig einen Ball fallen lassen oder dergleichen) und dieselbe Argumentation mithilfe der Kamera lässt sich auch auf andere Vorkommnisse von Scheinkräften (siehe z. B. Zentrifugalkraft) anwenden.
Ein didaktisches Problem bei Experimenten, die in irgendeiner Form das Gleichgewicht von Kräften thematisieren, besteht ferner in ihrer fehlenden Dynamik. Schüler könnten sich von vorherrschender Bewegungslosigkeit gelangweilt fühlen: Ruhende Systeme sind wenig spannend, wenn es sich nicht gerade um einen raffinierten Balanceakt handelt. Hinzu kommt, dass es nicht wirklich Experimente für den Fall des Kräftegleichgewichts bei konstanter Geschwindigkeit gibt, nicht zuletzt erschwert durch die Omnipräsenz von Gravitation und Reibung.
Wenngleich der Pendelwagen keine Lösung für die Behandlung des Präkonzepts bietet, ist dieses Experiment sehr wohl in der Lage, Kräftegleichgewicht in einer weniger statischen Art und Weise aufzuzeigen. Der Grundgedanke der Relativität einer Bewegung (Bewegung existiert in Bezugssystemen) ist dabei vordergründig. Nur weil etwas in Ruhe ist, heißt das nicht, dass es sich nicht bewegt. Alles ist eine Frage des Bezugssystems und erst das Bezugssystem entscheidet über Ruhe oder Bewegung.
Steckbrief
Eine Kurzübersicht der Kategorisierung des Experiments (nach Kircher et al.[4] (2015), S. 229 ff.) ist rechts tabelliert. Es folgen wenige Anmerkungen zur Zuweisung von Stichworten, die nicht selbsterklärend sind.
| Klassifikation des Experiments | ||||
|---|---|---|---|---|
| Datenerfassung | qualitativ | quantitativ | ||
| Experimentator | Schüler | Lehrer | ||
| Unterrichtsphase | Einstieg | Verarbeitung | Vertiefung | |
| Geräteeinsatz | freihand | Messgeräte | Simulation | Gedanken |
| Ausführung | parallel | Versuchsreihe | ||
| Funktionelle Aspekte | ||||
| Phänomen zeigen | Konzept veranschaulichen | Grunderfahrung | Gesetze erfahren | Theorie qualitativ prüfen |
| Schülervorstellungen | Technik und Alltag | Denkanstöße | Vorstellung aufbauen | Gesetze prüfen |
| Physikalisches Arbeiten | Interesse wecken | Nachhaltige Eindrücke | Meilensteine | |
Der Pendelwagen thematisiert Scheinkräfte und ist entsprechend spät in die Verarbeitungsphase des Unterrichts eingegliedert, wenngleich er überhaupt erst der Motivation des Scheinkraftbegriffs dient. Im Wesentlichen ist das eine Frage der Auslegung, allerdings wird ein gewisses Verständnis des Kraftbegriffs vorausgesetzt und der Begriff "Scheinkraft" taucht im Berliner Curriculum gar nicht erst auf.
Je nachdem, für welche Variante des Aufbaus man sich entscheidet, ist der Pendelwagen als Freihandexperiment oder als Experiment mit Messgeräten aufzufassen. Die Freihandvariante ohne Belehrungsapparat wird dabei empfohlen. Je besser der Experimentator an Alltäglichem anküpfen kann, desto freier ist die Sicht auf das Wesentliche, welches im Falle des (Schein-)kraftbegriffs schon genug im Abstrakten verborgen ist.
Das veranschaulichte Konzept ist das der Bewegung aus der Perspektive von Bezugssystemen. Die Frage nach der initialen Auslenkung wird qualitativ geprüft, günstigerweise unter Zuhilfenahme von Videoaufnahmen. Schülervorstellugen werden miteinbezogen, denn der Ruhebegriff erscheint im dynamischen Kontext. Das entspricht zwar nicht dem klassischen Präkonzept, dass alle kräftefreien Körper irrtümlicherweise ruhen müssen (in ruht das Pendel wirklich), allerdings fördert es die Aufmerksamkeit dafür, dass der Ruhezustand auch bloß eine Frage der Interpretation ist. Tiefere Reflexionen über die Relativität von Bewegungen sind Teil der Denkanstöße zur Wiederholung und Vertiefung.
Der Lehrende sollte sich in jedem Falle überlegen, auf welchem funktionellen Aspekt der Schwerpunkt des Experiments liegen soll, und zwar in Abhängigkeit der Feinziele zugehöriger Unterrichtseinheiten und den Voraussetzungen der Lernenden. Dieser Artikel dient im Wesentlichen der Darstellung des Experiments in seiner Ganzheit, wobei aus den vorgeschlagenen Gesichtspunkten angemessene zu selektieren sind.
Didaktische Hinweise
- Die Antwort auf die Frage nach der Auslenkung ist zwar nicht offensichtlich, kann allerdings auch "geraten" werden. Man bedenke, dass es nicht viele markante Auslenkungen des Pendels gibt, die intuitiv überhaupt in Frage kommen könnten. Bei (horizontale Ebene) wäre beispielsweise klar. Es ist nicht unwahrscheinlich, dass ein Schüler die Frage korrekt beantwortet, wenn man sie in die Runde stellt. Ermutigen Sie die Schüler zum Aufstellen von Hypothesen, die im Nachhinein verifiziert oder falsifiziert werden sollen.
- Der historische Bezug zu Einsteins glücklichstem Gedanken ist überlegenswert. Der wichtigste Ausschnitt des Zitats ist kurz und bündig (kann eventuell an die Tafel geschrieben werden) und eher greifbar für Schüler der siebten oder achten Klasse als irgendein Konzept der Relativitätstheorie. Auch Referenzen zur Populärkultur sind denkbar, beispielsweise sieht auch die menschliche Kanonenkugel frei fallende Objekte als geradlinig gleichförmige Bewegung.
- Es empfiehlt sich, bei der Präsentation des Experiments eine Links-Rechts-Dynamik einzuhalten (aus Sicht des Schülers), weil das der natürlichen Lese- und Schreibrichtung entspricht.
- Obwohl das Experiment als Demonstrationsexperiment kategorisiert ist, können Schüler beispielsweise in den Entwurf oder das Basteln des Pendelwagens miteinbezogen werden (falls Teilungsunterricht existiert, findet man womöglich eine sinnvolle Arbeitsaufteilung). Der Aufbau lässt genug kreative Freiheiten.
Versuchsanleitung
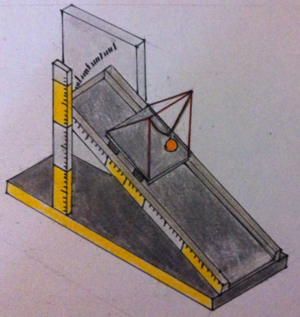
Der Vorteil des Pendelwagens ist, dass es für die fundamentale Erkenntnis der Relativität von Ruhe und Bewegung keines Belehrungsapparats bedarf. Der Aufbau ist denkbar einfach und ein Großteil der Materialien kann dem alltäglichen Tun entnommen werden. Wie genau der Pendelwagen zusammengebastelt wird, ist im Grunde unerheblich, allerdings sollte man auf irgendeine Art und Weise
- einen Pendelkörper wie z. B. die PHYWE Pendelkugel mit Haken (Artikel-Nr. 02801-00) oder einfach etwas Kompaktes wie eine Flasche Nasenspray,
- eine Schnur (möglichst wenig elastisch – Kordeln eignen sich gut),
- ein rollenden Untersatz sowie
- eine möglichst lange Fahrunterlage und optional
- eine oder besser zwei (Handy-)kameras
beschaffen können. Im folgenden Unterabschnitt werden verschiedene Varianten des Aufbaus vorgestellt, deren Materialien man vermutlich in einem jedem Physikvorbereitungsraum finden kann. Es sei jedoch ausdrücklich auf günstigere Methoden hingewiesen, je nachdem welche Materialien man auftreiben kann und wie viel Kreativität man in das Basteln investieren möchte. Beispielsweise wären
- ein Skateboard,
- ein Kugelstoßpendel mit abnehmbaren Schnüren,
- ein langes Brett (zwei Meter) und
- Heißkleber oder selbstklebendes Klettband
ein völlig legitimer Aufbau zur Demonstration unter Verwendung von Alltagsgegenständen (das Kugelstoßpendel besitzt gewissermaßen Kultcharakter und ist alltäglich genug).
Hinweis: Die Verwendung von Kameras ist optional, allerdings dauert die Bewegung je nach Länge der Fahrunterlage nur Sekundenbruchteile. Das Videografieren des Prozesses erleichtert die qualitative Auswertung des Experiments erheblich. Gängige Mobiltelefone reichen dafür völlig aus. Im Idealfall werden zwei Kameras verwendet, wobei eine zum Filmen des Pendelkörpers direkt am Pendelwagen angebracht wird und die andere zur Aufnahme der gesamten Szenerie irgendwo fest positioniert wird.
Die Aufnahmen können anschließend via WLAN an einen Computer übertragen und unter Verwendung eines geeigneten Players (z. B. VLC) betrachtet werden. Alternativ können die Videos zum Hervorheben bestimmter Ereignisse nachbearbeitet werden (Zeitlupe, Split Screen), was im letzten Abschnitt dieses Artikels vorgestellt wird.
Aufbau ("Physikvorbereitungsraum")
Bevor man mit dem Aufbau des Pendelwagens beginnt, sollte man die Frage der Verfügbarkeit einer Kamera beantworten. Experimente, die lediglich der Demonstration ohne Videoaufnahme dienen, können platz- und materialsparender aufgebaut werden (auf Kosten der Erkennbarkeit). Vorgestellt werden entsprechend unterschiedliche Varianten des Aufbaus.
Hinweis: Die Schnur des Pendelkörpers ist jeweils in V-Form am Gerüst anzubringen, damit Schwingungen lediglich entlang der Fahrunterlage möglich sind. Andernfalls gewinnt das System einen zusätzlichen Freiheitsgrad und man erzielt unter Umständen nicht den gewünschten Effekt.
Für die Neigung einer langen Fahrunterlage empfehlen sich zum Beispiel die Sprossen einer Leiter, die Höhendifferenz von Tisch und Stuhl oder ein paar Bücher. Solange die Bahn stabil aufliegt und der Neigungswinkel nicht zu groß (siehe Versuchsdurchführung) ist, ist das unerheblich.
Demonstration am Belehrungsapparat
Falls die Schule im Besitz einer verstellbaren schiefen Ebene mit zugehörigem Messwagen ist (an der die Orthogonalzerlegung der Gewichtskraft demonstriert werden kann), kann mit relativ wenig Aufwand ein kompakter Aufbau zusammengestellt werden, der allerdings keine Videoaufnahmen einer mitbewegten Kamera zulässt. Benötigt werden die folgenden oder vergleichbare Materialien:
- PHYWE Mess- und Experimentierwagen (Artikel-Nr. 11060-00)
- PHYWE Geneigte Ebene mit Rollkörper (Artikel-Nr. 11301-88, die Länge der Fahrbahn ist 50 cm)
- stabiler Draht (z. B. Kupferdraht, 2–3 mm Durchmesser) und Drahtzange
- Schnur und Pendelkörper
Es bietet sich an, den Draht zu einem dreiecksförmigen Gerüst (vgl. Skizze rechts) zu wickeln und am Messwagen zu befestigen. Am Wagen selbst befinden sich meist Löcher oder Haken, an denen der Kupferdraht fixiert werden kann, andernfalls kann man auf Klebeband oder Duct Tape zurückgreifen. Die oberen Eckpunkte der seitlichen Dreiecke können zu Schlaufen geformt werden, um die Schnur besser daran festbinden zu können. Wenn man einigermaßen geschickt mit Draht und Schnur umgeht, dauert der Aufbau etwa eine halbe Stunde.
Hinweis: Selbst bei Einstellung des niedrigsten Winkels der geneigten Ebene von PHYWE dauert die Bewegung bei der langen Schiene lediglich
und die Schüler sollten nach vorne gebeten werden, um den Effekt erkennen zu können. Abgesehen davon genügt dieser Aufbau der Demonstration und die Ruhelage des Pendelkörpers grenzt sich gut von den anderen Auslenkungen ab.
Drahtgerüst mit Smartphone-Halter
Um die Bewegung des Pendelwagens aus der Perspektive des mitbewegten Bezugssystems aufnehmen zu können, werden schwerere Messwagen mit einer höheren Belastbarkeit benötigt. Beispielhafte Materialien sind unten aufgeführt.
- PASCO 2.2 m Classic Dynamics System (Artikel-Nr. ME-9452B)
- stabiler Draht und Drahtzange
- Schnur und Pendelkörper
- ein Smartphone (günstigerweise mit einklappbarer Hülle)
- Gegengewichte (etwa vier 50g-Massenstücke)
Der Vorteil der PASCO-Messwagen ist, dass sie in der Oberseite zwei Bohrungen besitzen, an denen die zugehörige Ausrüstung festgeschraubt werden würde. Drahtschlaufen können demnach problemlos am Wagen fixiert und an anderen Stellen mit Klebeband verstärkt werden.
Zunächst einmal sollte überprüft werden, aus welcher Entfernung die Smartphone-Kamera die ganze Bewegung des Pendels filmen kann. Distanzen einer Größenordnung von 15 Zentimetern sind dabei nicht unüblich. Entsprechend groß ist die Hebelwirkung des Geräts, weswegen ein Gegengewicht an der anderen Seite des Drahtgerüsts angebracht werden muss. Ein beispielhaftes Aussehen ist rechts abgebildet (das Smartphone wird in die linke Schlaufe hineingelegt), die Justage erfolgt in Abhängigkeit der Länge des Hebels und der Masse des Smartphones. Die Kamera sollte auf das Pendel zentriert sein, weswegen die Drahtschlaufe für das Smartphone nicht ganz symmetrisch am Wagen angebracht ist.
Eine Smartphone-Hülle mit Kamera-Ausschnitt, die sich über den Bildschirm klappen lässt, ist hierbei überaus angemessen, um Kratzer am Gerät durch den Draht zu vermeiden. Der Aufbau ist insgesamt etwas wackelig, kostet jedoch nicht wesentlich mehr Aufwand als die zuvor beschriebene Variante und ein Smartphone sollte ebenfalls leicht aufgetrieben werden können. Kleine Abweichungen der Ruhelage sind auch vorwiegend darauf zurückzuführen, dass der Wagen beim Fahren etwas schwankt – was wiederum damit korreliert, wie frei sich das Gegengewicht bewegen kann.
Hinweis: Massenstücke mit Haken stellen ein gut skalierbares Gegengewicht dar, allerdings sollten diese nicht untereinander aufgehängt, sondern eher als Bündel am Gerüst mit wenig Bewegungsfreiheit fixiert werden. Sobald das Gegengewicht zum Pendeln in der Lage ist, erhält das System einen weiteren Freiheitsgrad und auch hier könnte das die Beobachtung eventuell beeinflussen.
Stabiles Gerüst
Die letzte hier vorgestellte Variante verwendet stabilere Materialien eines Physikvorbereitungsraums und ermöglicht insbesondere Videoaufnahmen mit einer Kamera (in erster Linie kein Smartphone). Benötigt werden die folgenden oder ähnliche Materialien:
- PASCO 2.2 m Classic Dynamics System (Artikel-Nr. ME-9452B)
- Stativmaterial (abhängig von der Belastbarkeit des Wagens)
- 6 Stangen der Länge ≈20 Zentimeter, 4 davon mit Gewinde und passendem Aufsatz
- 4 Kreuzmuffen
- Pappe (in etwa A4)
- Kamera
- doppelseitiges Klebeband oder selbstklebendes Klettband
- ggf. Gegengewichte
- optional: Geodreieck/Winkelmesser (breiter als 20 Zentimeter)
Die Pappe ist dabei mit der langen Seite quer am Wagen zu befestigen (vgl. Abbildung), damit Kamera und Gegengewicht an beiden Seiten platziert werden können. Bei PASCO-Wagen kann die Pappe direkt angeschraubt werden, andernfalls bedient man sich doppelseitigen Klebebands oder dergleichen. Falls die Kamera zusätzlich geneigt werden muss, kann zusätzlich ein kleines Plättchen aus Pappe für die korrekte Positionierung aufgeklebt werden.
Die vier Stativstangen mit Gewinde werden ebenfalls in die Pappe gesteckt und von der Unterseite zugeschraubt, bis sie sich nur noch wenig neigen lassen. Mit den Kreuzmuffen und den verbleibenden Stativstangen werden zwei Querverstrebungen erstellt, an denen das Pendel befestigt wird. Das Hinzufügen weiterer Querstangen würde den PASCO-Wagen zu sehr belasten, weswegen man auf leichtere Materialien (z. B. Plastikröhren oder Draht) zurückgreifen müsste. Der Wagen ist allerdings auch ohne zusätzliche Verbindungen stabil genug (der Aufbau muss lediglich nach mehrfacher Benutzung gerade gerückt werden).
Für den Fall, dass die Belastung durch die Kamera die Pappe nach unten drückt, kann einer zu starken Wölbung durch das Fixieren einer Metallstange (oder Schaschlikspießen) mit Klebeband entgegengewirkt werden. Eine asymmetrische Verteilung der Stativstangen zieht eine Schwerpunktverlagerung des Wagens nach sich, was durch eine Verschiebung der Querstangen korrigiert werden kann.
Der Aufbau kann zusätzlich mit einem Geodreieck versehen werden, dessen Skala in Richtung Kamera zeigt (Befestigung mit Klebeband an den Stativstangen). Das ist insofern vorteilhaft, als die Neigung der Ebene in der Videoaufnahme abgelesen werden kann, wenn das Pendel senkrecht zum Erdboden hängt (Subtraktion des abgelesenen Winkels von 90 Grad im Betrag).
Versuchsdurchführung
Bringen Sie den Wagen ins Rollen. Der Versuch wird für verschiedene initiale Auslenkungen des Pendels auf verschieden geneigten Ebenen qualitativ wiederholt. Es bieten sich die unten aufgeführten markanten Auslenkungen des Pendels an.
Pendel steht senkrecht zum Erdboden Pendel steht senkrecht zur Ebene große Auslenkung links von der Ruhelage große Auslenkung rechts von der Ruhelage
Da es nicht viel zur Durchfürung an sich zu sagen gibt, sei im Folgenden auf ein paar Dinge hingewiesen, die beachtet werden sollten.
- Es wird ausdrücklich empfohlen, das Experiment (insbesondere Aufnahmen mit einer am Wagen fixierten Kamera) zu zweit durchzuführen. Während sich eine Person um die initiale Auslenkungs des Pendels kümmert und im Anschluss den Wagen loslässt, sollte sich am unteren Ende der Schiene eine weitere Person zum Abfangen des rollenden Wagens positionieren, um eine Beschädigung der Gerätschaften zu vermeiden. Der Pendelwagen erreicht bei einer Höhendifferenz von beispielsweise eine Endgeschwindigkeit von , was bei breiten und schweren Wagen nicht zu unterschätzen ist.
- Zu starke Neigungen der schiefen Ebene sind zu vermeiden, da der Wagen andernfalls in kürzerer Zeit auf seine Endgeschwindigkeit beschleunigt wird und sehr leicht entgleisen kann. Es empfiehlt sich, die Neigung bei größeren Aufbauten nur mit äußerster Vorsicht zu überschreiten. Bei einer zwei Meter langen Schiene entspricht das einer Höhendifferenz von einem Meter (in etwa Hüfthöhe).
Ergebnisse
Unabhängig vom gewählten Aufbau ist die Beobachtung klar (auch in Sekundenbruchteilen): Das Pendel bleibt für in der Luft "stehen", beginnt jedoch für alle anderen Auslenkungen instantan zu schwingen. Unten tabelliert sind eine Aufnahme am Drahtwagen mit Smartphone-Halter und sieben Aufnahmen am stabilen Wagen für zwei Neigungen der schiefen Ebene mit durchschnittlichem Einzelbild (vgl. Verarbeitung der Videoaufnahmen) des jeweiligen Videos.
Die Links-Rechts-Dynamik wurde hier nirgends eingehalten. Im Zweifelsfall sind die Videos horizontal zu spiegeln (siehe letzter Satz des letzten Abschnitts).
| Aufnahme in zehnfacher Zeitlupe | Arithmetisches Mittel der Einzelbilder |
|---|---|

| |
| Smartphone-Aufnahme: Auslenkung senkrecht zur Ebene Der Effekt ist beim Drahtwagen einigermaßen gut zu beobachten. Das Pendel schwingt minimal. Ein Blick auf das durchschnittliche Einzelbild zeigt, dass der Pendelkörper sogar eher "wackelt" als schwingt. Tatsächlich schwankt der Pendelwagen sehr und zeigt selbst eine transparente Spur im durchschnittlichen Frame (gut zu erkennen am rechten Draht). Auch das Gegengewicht im Hintergrund besitzt eine große Bewegungsfreiheit. Insgesamt trägt die massive Hebelwirkung des Smartphones sehr zur Instabilität des gesamten Systems bei und das Wackeln des Pendels ist im Wesentlichen das Wackeln des Wagens. Nichtsdestoweniger wirkt die Aufnahme gelungen, die minimale Pendelbewegung würde in Relation zu anderen Auslenkungen auch wenig ins Gewicht fallen. | |
| [[1]] | 
|
| Schwach geneigte Ebene: Auslenkungen senkrecht zur Ebene, senkrecht zum Boden und um zwei große Winkel Gezeigt sind oben links, oben rechts sowie und unten links bzw. rechts. Der schwere, stabile Wagen mit verminderter Hebelwirkung der Kamera zeigt den Effekt noch besser als der Drahtwagen mit Smartphone-Halter. Die obere linke Auslenkung wird beibehalten und alle anderen schwingen direkt zu Beginn der Bewegung. Die Ruhelage ist im durchschnittlichen Einzelbild auch als solche zu identifizieren, denn statt einer transparenten Spur sieht man den Pendelkörper an einer Position fixiert. Die anderen Bewegungen verwischen zu einem stetigen Verlauf und sind weniger sichtbar, je größer die Amplitude der Schwingung ist. | |
| [[2]] | 
|
| Stark geneigte Ebene: Auslenkungen senkrecht zur Ebene, senkrecht zum Boden und um einen großen Winkel Die Anordnung der initialen Auslenkungen ist wie oben, allerdings wird hier statt die Sicht des räumlich festen Bezugssystems gezeigt. Die Beobachtungen für unterschiedliche Neigungen sind im Wesentlichen identisch, dennoch empfehlt sich eine Variation von für den "Konsistenzcheck" (die Theorie soll für verschiedene überprüft werden). Anhand der Aufnahme der gesamten Szenerie lässt sich der Relativitätscharakter der Bewegung gut erklären (begleitet durch eine qualitative Auswertung), denn obwohl das Pendel nicht schwingt, bewegt es sich aus Sicht der fixierten Kamera beschleunigt. Die beschleunigte Bewegung des Wagens auf der schiefen Ebene lässt sich gut anhand des mittleren Einzelbilds erkennen, denn die Deckkraft der Spur ist indirekt proportional zur Geschwindigkeit der Apparatur (je länger der Wagen an einer Position verbleibt, desto stärker fallen diese Frames beim Mitteln ins Gewicht). | |
Auswertung
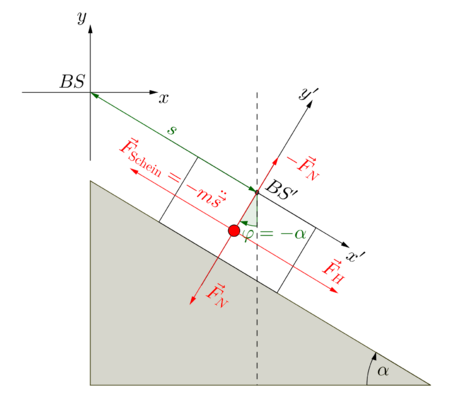
Im Falle erfährt der Ursprung von gegenüber dem Ursprung von die Hangabtriebsbeschleunigung. Insbesondere spürt die Kamera dieselbe Beschleunigung wie der Pendelwagen. Die Anwendung der Transformationsformel auf die Pendelmasse liefert
und das Pendel ist in Ruhe (Abbildung rechts). Wenngleich diese Formel niemals an einer Schultafel erscheinen wird, entspricht das Vorgehen der Schüler genau dieser Gleichungskette – allerdings rückwärts. Sie schließen im Best Case gewissermaßen auf die Gleichung:
Diese Gleichung ist zwar genauso inadäquat wie die vorige, allerdings lässt sich hierfür eine geeignete horizontale Reduktionsebene in Form einer Gedankenkette finden, die mit den Schülern durchlaufen werden kann. Sie starten vom Vorwissen und schließen mithilfe der Beobachtung auf die Notwendigkeit einer Scheinkraft aus Sicht der mitbewegten Kamera.
- Vorwissen
- Auf den Pendelkörper wirken die Gewichtskraft und die Fadenkraft (letztere Gleichheit gilt nur wegen ).
- Ist ein Körper in Ruhe, wirkt keine Kraft auf ihn oder er befindet sich im Kräftegleichgewicht.
- Beobachtung
- Der Pendelkörper ist aus Sicht der mitbewegten Kamera in Ruhe.
- Schlussfolgerung
- Aus Sicht der mitbewegten Kamera ist der Pendelkörper im Kräftegleichgewicht.
- Es muss demnach eine Kraft geben, die die Hangabtriebskraft kompensiert. Der Kraftpfeil ist genauso lang wie der der Hangabtriebskraft und zeigt in die andere Richtung.
- Diese Kraft nennt man Scheinkraft. Nicht alle Kameras "sehen" die Scheinkraft.
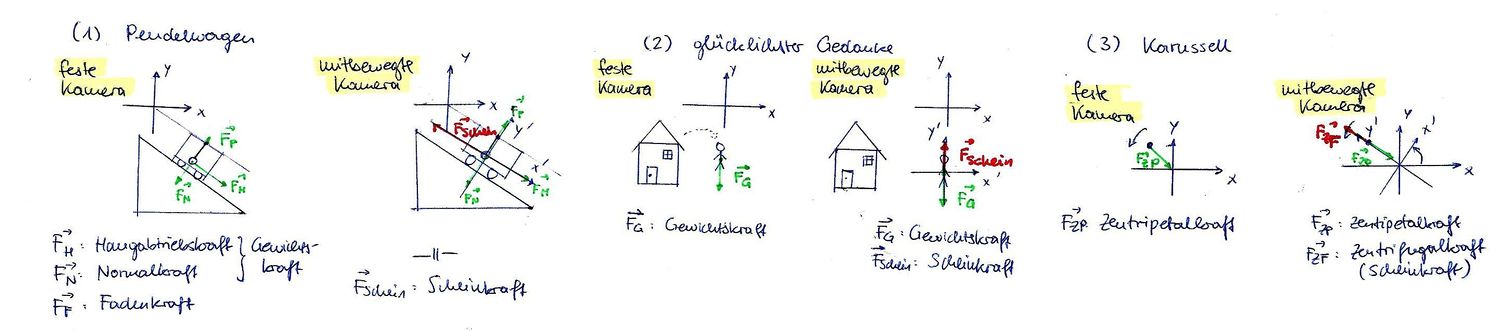
Die Schüler sollten die Kraftpfeile für den Fall aus der Sicht beider Bezugssysteme zeichnen. Eine tabellarische Darstellung beider Skizzen ermöglicht auch hier einen guten Kontrast. Es ist weiterhin angemessen, die Kräfte zu benennen – die Scheinkraft soll explizit als solche bezeichnet werden. Auch die Koordinatenachsen beider Systeme können in der jeweiligen Skizze gezeichnet und als "Fadenkreuz" der fixierten bzw. mitbewegten Kamera gedeutet werden. Die Kraftpfeile können mit vektoriellen Symbolen beschriftet werden, ohne dass der Vektorbegriff fallen muss (es sollte einleuchtend genug sein, Pfeilgrößen mit Pfeilen zu beschriften).
Dasselbe Vorgehen lässt sich auch auf andere Bewegungen anwenden, bei denen leicht ein Bezugssystem gefunden kann, welches diese in Ruhe überführt. Unten abgebildet sind Skizzen, wie sie an der Tafel und bei den Schülern auf Papier erscheinen könnten.
Verarbeitung der Videoaufnahmen
Das Nachbearbeiten von Videos stellt sich für Laien wie den Autor dieses Artikels als schwieriges Unterfangen heraus, was nicht zuletzt von der grundlegenden Struktur eines Videoformats herrührt. Dieser Abschnitt versucht deswegen, den Verarbeitungsprozess so zu dokumentieren, dass man weitgehend ohne Vorkenntnisse zu den Ergebnissen gelangen kann, die in diesem Artikel präsentiert werden. Von einer Schritt-für-Schritt-Anleitung wird jedoch abgesehen, um den Rahmen des Artikels nicht zu überdehnen.
Das Grundproblem bei der Bearbeitung von Videos ist, dass die Dateiendung (MP4, AVI, MOV, FLV und so fort) eine relativ aussagelose Eigenschaft ist, wenn es um das Videoformat geht. Ausschlaggebend für die Datei sind die Video- und Audiospur, aus denen sie besteht und die ihr Format bestimmen. Eine Software zum Komprimieren und Dekomprimieren von Mediendateien heißt Codec. Welche Videoformate ein Computer abspielen kann, hängt im Wesentlichen davon ab, welche Codecs auf ihm installiert sind.
Für einfache Aufgaben wie das Herausschneiden einer bestimmten Videosequenz gibt es zahlreiche Programme, von denen das intuitivste nach persönlicher Präferenz auszuwählen ist. Die dargestellten Ergebnisse wurden mit der freien Software VirtualDub bearbeitet. Der Vorteil dieser Software ist, dass das Video bei der Selektion eines bestimmten Ausschnitts nicht neu berechnet (gerendert) muss, was bei vielen Aufnahmen kumulativ Zeit spart. Ein Ausschnitt des Videos lässt sich leicht spezifizieren, indem man im Menüpunkt Video → Select Range eine Startzeit und die gewünschte Dauer einträgt.
Da die Bewegung des Pendels selbst auf einer zwei Meter langen Schiene bei flacher Neigung nicht wesentlich länger als eine Sekunde dauert, bietet es sich an, den selegierten Ausschnitt in Zeitlupe abzuspielen. Dies geschieht durch Verminderung der FPS, es sollen weniger Einzelbilder pro Zeiteinheit abgespielt werden. Bei VirtualDub erreicht man das über den Menüpunkt Video → Framerate → Change Framerate to (fps) durch Angabe einer geeigneten Zahl (das Vermindern der Bildfrequenz von 30 auf 3 entspricht beispielsweise einer zehnfachen Zeitlupe). Zu beachten ist, dass Video- und Audiospur durch das Ve l;ndern der Framerate nicht mehr synchron zueinander Verlaufen. Das Anpassen der Tonspur erfolgt bei VirtualDub ein wenig unintuitiver.[8]
Im Wesentlichen sind diese grundlegenden Bearbeitungsschritte ausreichend, um brauchbare Ergebnisse zu erhalten. Der Effekt des ruhenden Pendels im mitbewegten Bezugssystem der Kamera lässt sich in Zeitlupe gut nachvollziehen. Es gibt jedoch noch weitere Möglichkeiten, die Aufnahmen angemessen zu präsentieren:
- Der Bewegungsverlauf des Pendels kann genauer betrachtet werden, indem man den Durchschnitt aller Frames des gewählten Ausschnitts berechnen und als Bild ausgeben lässt. Filmt man die Bewegung vor einem möglichst einheitlichen Hintergrund (beispielsweise einer Wand), ist eine transparente Spur des Pendelkörpers zu sehen. Dabei gilt: Je größer die Amplitude und folglich die Geschwindigkeit des Pendelkörpers, desto geringer ist dessen Deckkraft. Im Falle des ruhenden Pendels sieht man kaum Transparenz, weil sich der Pendelkörper nur wenig (im Idealfall gar nicht) bewegt hat.
- Das gleichzeitige Abspielen von mehreren Aufnahmen in einem gemeinsamen Video ermöglicht einfache Vergleiche zwischen verschiedenen Auslenkungen des Pendels oder den Bewegungen im jeweiligen Bezugssystem.
Ein Schnittprogramm wie VirtualDub reicht dafür nicht mehr aus, weswegen sich die Installation der unten aufgeführten Programme anbietet.
- FFmpeg (Verarbeitung von Videos)
- ImageMagick (Verarbeitung von Bildern)
Die angegebenen Programme besitzen keine grafische Benutzeroberfläche und lassen sich stattdessen über die Kommandozeile bedienen. Unter Windows kann man diese durch Eintippen von cmd in die Suchleiste aufrufen. Das textbasierte Arbeiten mit der Kommandozeile ist zu Beginn etwas gewöhnungsbedürftig, erweist sich für automatisierbare Prozesse (z. B. der Berechnung des durchschnittlichen Bilds aller Einzelbilder in einem Video) allerdings als überaus praktisch. Auf ein Tutorial wird im Folgenden verzichtet, stattdessen wird in diesem Abschnitt auf diejenigen Befehle der Programme eingegangen, derer es zur Ausgabe der hier präsentierten Ergebnisse bedarf. Oftmals reicht das Kopieren der hier dargestellten Eingaben in die Kommandozeile aus (unter Anpassung der Dateinamen, außerdem ist STRG+V im cmd standardmäßig ausgeschaltet – Einfügen erfolgt also per Rechtsklick).
Zunächst einmal wird es an verschiedenen Stellen des Verarbeitungsprozesses nötig sein, ein Video in ein anderes Dateiformat zu konvertieren. Kameras speichern die Aufnahmen beispielsweise als festgelegtes Format, allerdings sind Programme für den Videoschnitt in ihrer Kompatibilität hinsichtlich gewisser Formate eingegrenzt (beispielsweise ist VirtualDub vorwiegend für AVI-Dateien konzipiert). Die Umwandlung einer Videodatei video.xxx in ein anderes Format video.yyy geschieht in FFmpeg auf sehr einfache Art und Weise mit dem folgenden Befehl:
ffmpeg -i video.xxx video.yyy
Es kann bei der Konvertierung zu Qualitätsverlusten oder Bildfehlern kommen, die an Störsignale erinnern. Welche Videoformate abgespielt und verarbeitet werden können, ist davon abhängig, welche Codecs auf dem Computer vorhanden sind. Die Installation von Software wie ffdshow kann unter diesen Umständen Abhilfe schaffen. Die hier gezeigten Endergebnisse wurden mit dem H.264-Standard ohne Qualitätsverlust konvertiert:
ffmpeg -i video.avi -c:v libx264 video.mp4
Berechnung des durchschnittlichen Einzelbilds
Von der Datei video.mp4 sei im Folgenden das durchschnittliche Einzelbild zu berechnen. Das Vorgehen kann man dabei in zwei Schritte untergliedern.
- Mithilfe von FFmpeg werden Einzelbilder bei fixierter Bildfrequenz (z. B. 10 FPS) aus dem Video extrahiert und als Bilddatei gespeichert.
- Aus den ausgewählten Frames wird das durchschnittliche Bild unter Verwendung von ImageMagick berechnet.
Es ist ratsam, am Ort der Videodatei ein Unterverzeichnis images anzulegen, um die Einzelbilder dort speichern zu lassen. Je nachdem, wie hoch die Bildfrequenz gewählt wurde und wie lang der Ausschnitt dauert, erhät man eine große Anzahl image001.jpg, image002.jpg, ..., image500.jpg, ... von Dateien, die das Verzeichnis des Videos andernfalls überschwemmen würden. Die Extraktion von Frames aus video.mp4 bei einer Bildfrequenz von 10 FPS und das Abspeichern ebendieser unter dem Dateinamen imageXXX.jpg im angelegten Unterordner images, geschieht mit diesem Befehl:
ffmpeg -i video.mp4 -vf fps=10 images/image%03d.jpg
Je höher der Wert für fps gewählt wird, desto mehr Frames werden gespeichert und desto verschmierter erscheint die transparente Spur des Pendelkörpers beim durchschnittlichen Einzelbild. Das Symbol %03d ist ein Platzhalter für eine dreistellige Ganzzahl mit führenden Nullen (001, 002, ..., 500, ...). Es wird empfohlen, die Bilder mit der Dateiendung JPG abzuspeichern: Einerseits ist das verlustbehaftete Grafikformat für die weichen Farbübergänge auf Fotos gut geeignet – ausschlaggebender ist jedoch, dass der Prozess des arithmetischen Mittelns erheblich verkürzt wird. Salopp formuliert muss bei einem Bitmap-Format wie PNG für jeden Pixel, welcher wiederum drei ganzzahlige Farbwerte beinhaltet, von hunderten Bildern der jeweilige Mittelwert berechnet werden. Dies strapaziert handelsübliche Computer sehr und dauert bei einer großen Anzahl von Einzelbildern wesentlich länger. Das Format JPG speichert die Farbinformation günstiger auf Kosten der Qualität, allerdings wird das gemittelte Einzelbild in Sekundenschnelle ausgegeben. Das Durchschnittsbild avg.jpg wird erzeugt durch:
convert images/*.jpg -average avg.jpg
Der Asterisk (*) ist ein Platzhalter und sorgt dafür, dass alle Dateien mit der Endung JPG im Ordner images miteinbezogen werden sollen.
Hinweis: Unter Windows kommt es beim Befehl convert zu einer Doppelbelegung mit einem anderen Programm, weswegen er durch den Pfad von convert.exe im Verzeichnis von ImageMagick zu ersetzen ist. Dieser sieht in etwa so aus (die Anführungszeichen müssen übernommen werden, wenn der Pfad Leerzeichen enthält):
"/Program Files/ImageMagick-6.9.0-Q16/convert" images/*.jpg -average avg.jpg
Der genaue Dateiname hängt von der Version von ImageMagick ab.
Tabelliert sind unterschiedliche Ergebnisse für den durchschnittlichen Frame desselben Videos in Abhängigkeit der Wahl des FPS-Parameters. Es ist weiterhin angegeben, wie lange die Berechnung der einzelnen Bilddatei für die Formate JPG und PNG gedauert hat, um den zeitlichen Unterschied quantitativ ersichtlich zu machen.
| Videodatei | fps=3 | fps=10 | fps=30 | |
|---|---|---|---|---|
| 112 Frames bei 25 FPS (00:00:04.480, Zeitlupe ×3) | 14 Bilddateien | 45 Bilddateien | 134 Bilddateien | |
| Rechenzeit in Sekunden basierend auf 20 Messungen, Stichprobenmittel ± Streuung des Mittelwerts bei 8 GB RAM und 4× 4.2 GHz CPU |
JPG | |||
| PNG | ||||
| Erläuterung | Die einzelnen Positionen des Pendelkörpers sind klar erkennbar. Die Bildfrequenz muss für ein glattes Ergebnis höher gewählt werden. | Der Übergang zwischen den einzelnen Positionen des Pendelkörpers ist weicher, man erkennt eine nahezu kontinuierliche, transparente Spur. | Es werden mehr Bilder gespeichert, als es überhaupt unterschiedliche Frames gibt. Der optische Unterschied zur Extraktion mit 10 FPS ist vernachlässigbar. | |
Mehrere Aufnahmen in einem Video
Die Kombination mehrerer Videos zu einer Art Split Screen ist insofern vorteilhaft, als
- verschiedene initiale Auslenkungen des Pendels auf derselben Neigung der Schiene,
- dieselben initialen Auslenkungen des Pendels auf verschiedenen Neigungen der Schiene oder
- dieselbe Bewegung des Pendels mit zwei Kameras verschiedener Perspektiven (in zwei verschiedenen Bezugssystemen)
zeitgleich miteinander verglichen werden können. Eine detaillierte Erläterung der etwas länglichen Eingaben zur Erstellung der Videomosaike wird hierbei ausgespart – es sei jedoch explizit auf externe Quellen hingewiesen, die eine derartig genaue Beschreibung jeder syntaktischen Einheit vornehmen.[9]
Hinweis: Da es schwierig ist, sich auf zwei Ereignisse gleichzeitig zu konzentrieren, sind längere Videos für die Präsentation von Aufnahmen als Split Screen besser geeignet. Bei zehnfacher Zeitlupe sollte man beispielsweise genug Zeit haben, die einzelnen Aufnahmen gesondert zu betrachten und miteinander zu vergleichen. Aufgrund der Maximalgröße beim Upload von Dateien sind Aufnahmen hier in dreifacher Zeitlupe dargestellt.
Vergleich verschiedener Auslenkungen bei identischer Neigung der Ebene
Die Bestätigung der Theorie – also dem Ergebnis, welches man durch Aufstellen der Bewegungsgleichungen für das System oder durch Betrachten der Scheinkräfte berechnen kann – erfolgt am besten über den Vergleich der Pendelbewegungen bei variierender initialer Auslenkung. Auf diese Art und Weise lässt sich am besten zeigen, dass die Amplitude der Pendelbewegung für den Fall der Ausrichtung senkrecht zur Schiene tatsächlich vernachlässigbar klein in Relation zu anderen Auslenkungen beim Loslassen des Pendelwagens ist. Man stellt fest, dass der Pendelkörper bei großen Auslenkungen oder bereits beim Hängenlassen instantan zu schwingen beginnt und dass das bei nicht der Fall ist. Betrachtet man die Aufnahmen demnach gleichzeitig, wird diese Erkenntnis durch den auftretenden Kontrast zwischen Dynamik und Statik besonders hervorgehoben.
Angenommen, es liegen die gut miteinander vergleichbaren Aufnahmen
- Erdboden.mp4 des hängenden Pendels senkrecht zum Erdboden mit ,
- Ebene.mp4 der Auslenkung senkrecht zur Ebene mit ,
- Links.mp4 der Auslenkung um irgendeinen großen Winkel links von der Ruhelage sowie
- Rechts.mp4 der Auslenkung um irgendeinen großen Winkel rechts von der Ruhelage
mit den Maßen 1920 × 1080 vor. Dann ist es die intuitivste Lösung, die Videos in einer 2×2-Matrix anzuordnen, da das Resultat das Seitenverhältnis der einzelnen Aufnahmen beibehält. Die Videos sollten in etwa gleich lang sein – geringe Abweichungen in der Gesamtzahl der Frames (herrührend vom Schnitt oder von einer zufälligen Veränderung der Bewegungsdauer) sind allerdings unerheblich, da das Ende einer festgelegten Aufnahme das Ende der anderen nach sich zieht und dies bei vier zeitgleich abgespielten Aufnahmen nicht auffallen wird.
Das Vorgehen ist, die einzelnen Aufnahmen auf 960 × 540 zu skalieren (halbierte Seitenlängen, insbesondere bleibt das Seitenverhältnis darunter invariant) und an die richtige Stelle im Bild zu verschieben. Das erfolgt unter Angabe einer - und -Koordinate für die Verschiebung nach rechts bzw. unten. Verschoben wird der oberste linke Punkt der Aufnahme, ausgehend vom obersten linken Punkt des Bildschirms. Das Ergebnis Auslenkungen.mp4, dessen Eingabe und Ausgabe am Ende dieses Unterabschnitts tabelliert sind, erzeugt man mit dem folgenden Befehl:
ffmpeg -i Ebene.mp4 -i Erdboden.mp4 -i Links.mp4 -i Rechts.mp4 -filter_complex "nullsrc=size=1920x1080 [base]; [0:v] setpts=PTS-STARTPTS, scale=960x540 [upperleft]; [1:v] setpts=PTS-STARTPTS, scale=960x540 [upperright]; [2:v] setpts=PTS-STARTPTS, scale=960x540 [lowerleft]; [3:v] setpts=PTS-STARTPTS, scale=960x540 [lowerright]; [base][upperleft] overlay=shortest=1 [tmp1]; [tmp1][upperright] overlay=shortest=1:x=960 [tmp2]; [tmp2][lowerleft] overlay=shortest=1:y=540 [tmp3]; [tmp3][lowerright] overlay=shortest=1:x=960:y=540" -c:v libx264 Auslenkungen.mp4
Syntaktisch ist dieser zergliedert in
- die Erstellung eines leeren Platzhalters mit den Maßen 1920 × 1080,
- die Platzierung des nullten Inputs (Ebene.mp4) oben links (ohne Verschiebung),
- die Platzierung des ersten Inputs (Erdboden.mp4) oben rechts (verschoben um die skalierte Breite von 960 in -Richtung),
- die Platzierung des zweiten Inputs (Links.mp4) unten links (verschoben um die skalierte Höhe von 540 in -Richtung) sowie
- die Platzierung des dritten Inputs (Rechts.mp4) unten rechts (in beide Richtungen verschoben).
Die Reihenfolge der einzelnen -i XXX.mp4 ist demnach ausschlaggebend für die Position der jeweiligen Aufnahme und muss im Befehl entsprechend konsistent eingehalten werden. Bei geringfügigen Änderungen des Befehls ist darauf zu achten, dass auf die letzte Anweisung in den Anführungszeichen kein Semikolon folgt, andernfalls kommt es zu unintuitiv erscheinenden Fehlermeldungen.
| Input | Output | |
|---|---|---|
| (0) Ebene.mp4 |
(1) Erdboden.mp4 |
Auslenkungen.mp4 |
| (2) Links.mp4 |
(3) Rechts.mp4 | |
Vergleich des ruhenden und des mitbewegten Bezugssystems
Falls im Best Case zwei Kameras für das Filmen des Experiments zur Verfügung stehen, können die Unterschiede der Bewegungen des Pendelkörpers im zugehörigen Bezugssystem auch visuell – also fern von der suggestiven Betrachtung "Stellt euch vor, ihr säßt vor dem/im Pendelwagen." – klar aufgezeigt werden. Die Dynamik der Perspektive einer im Raum fixierten Kamera kontrastiert gut mit der statischen Perspektive der am Pendelwagen befestigten Kamera. Die im Raum aufstellte Kamera schaut außerdem nicht dem Pendelwagen hinterher (wie man es selbst vermutlich tun würde), sondern behält Position und Ausrichtung bei und entspricht damit der exakten Perspektive des ruhenden Bezugssystems.
| Input | Output |
|---|---|
| (0) RuhendesSystem3.mp4 |
BewegtesUndRuhendesSystem3.mp4 BewegtesUndRuhendesSystem3_Gespiegelt.mp4 |
| (1) BewegtesSystem3.mp4 |
Es seien im Folgenden BewegtesSystem3.mp4 und RuhendesSystem3.mp4 Aufnahmen der mitbewegten bzw. der aufgestellten Kamera in dreifacher Zeitlupe. Die Videos sollen so kombiniert werden, dass sich die Perspektive der aufgestellten Kamera über den gesamten Bildschirm erstreckt (die Aufnahme umfasst die gesamte Szenerie, demnach ist der Pendelkörper kleiner im Bild und schwerer zu erkennen) und die Sicht der mitbewegten Kamera irgendeine Position des Hintergrunds überlagert, in der keine Bewegung abläuft. Im unten aufgeführten Beispiel ist das die obere linke Ecke, in welcher lediglich eine Wand des Raums zu erkennen ist.
Der Befehl für das gewünschte Ergebnis (rechts tabelliert) lässt sich analog zum vorigen Beispiel als
ffmpeg -i RuhendesSystem3.mp4 -i BewegtesSystem3.mp4 -filter_complex "nullsrc=size=1920x1080 [base]; [0:v] setpts=PTS-STARTPTS, scale=1920x1080 [background]; [1:v] setpts=PTS-STARTPTS, scale=640x360 [small]; [base][background] overlay=shortest=1 [tmp1]; [tmp1][small] overlay=shortest=1" -c:v libx264 BewegtesUndRuhendesSystem3.mp4
formulieren (wobei das nicht die eleganteste, wenngleich eine zweckmäße Schreibweise ist) und ist in
- die Erstellung eines leeren Platzhalters mit den Maßen 1920 × 1080,
- die Platzierung des nullten Inputs (Hintergrundaufnahme: RuhendesSystem3.mp4) mit denselben Maßen oben links (keine Verschiebung nach rechts/unten) sowie
- die Platzierung des ersten Inputs (Pendelaufnahme: BewegtesSystem3.mp4) mit den Maßen 640 × 360 oben links (ein Drittel der Seitenlängen, keine Verschiebung nach rechts/unten)
untergliedert. Verliefe die Dynamik günstigerweise von links nach rechts und nicht – wie hier dargestellt – umgekehrt, so würde man die Pendelaufnahme vermutlich in der oberen rechten Ecke platzieren wollen und der Ausdruck
[tmp1][small] overlay=shortest=1
müsste unter Beibehaltung aller Maße zu
[tmp1][small] overlay=shortest=1:x=1280
angepasst werden (die Pendelaufnahme wird um x = 1920 - 640 = 1280 nach rechts verschoben). Die Links-Rechts-Dynamik kann im Nachhinein auch durch horizontale Spiegelung des Videos via
ffmpeg -i BewegtesUndRuhendesSystem3.mp4 -vf "hflip" BewegtesUndRuhendesSystem3_Gespiegelt.mp4
erreicht werden, wenn man sich nicht von den resultierenden Auffälligkeiten wie spiegelverkehrt beschriebenen Tafeln irritieren lässt.
Literatur
- ↑ Körner, T. W. (1998): Mathematisches Denken. Vom Vergnügen am Umgang mit Zahlen. Springer Basel AG.
- ↑ Kling, J. (2015): Rutschendes Pendel. Verfügbar unter http://people.physik.hu-berlin.de/~jordi/documents/ktp2015/lsg/RutschendesPendel_aVqDpPq3.pdf (Zugriff am 12.03.2016 um 12:57).
- ↑ 3,0 3,1 3,2 Kling, J. (2015): Kräfte im Gleichgewicht. Verfügbar unter http://people.physik.hu-berlin.de/~jordi/documents/dpr/main.pdf (Zugriff am 11.03.2016 um 14:22).
- ↑ 4,0 4,1 4,2 4,3 Kircher, E.; Girwidz, R.; Häußler, P. (2015): Physikdidaktik. Theorie und Praxis. Springer Verlag Berlin Heidelberg, Dritte Auflage.
- ↑ 5,0 5,1 Wiesner, H.; Schecker, H.; Hopf, M. (2015): Physikdidaktik kompakt. Aulis Verlag.
- ↑ Boczianowski, F. (2007): Vom Tragen zum Tragwerk. Eine Einführung des Kraftbegriffs durch körperliche Erfahrungen. Erschienen in Naturwissenschaften im Unterricht Physik, Friedrich Verlag GmbH, Heft 98.
- ↑ Senatsverwaltung für Bildung, Jugend und Sport (2006): Rahmenlehrplan für die gymnasiale Oberstufe. Physik. Berlin, Erste Auflage.
- ↑ Dedoimedo (2012): How to record slow-motion video and audio in VirtualDub. Verfügbar unter http://www.dedoimedo.com/computers/virtualdub-slow-audio-video.html (Zugriff am 06.03.2016 um 19:28).
- ↑ FFmpeg Wiki (2013): Create a mosaic out of several input videos. Verfügbar unter https://trac.ffmpeg.org/wiki/Create%20a%20mosaic%20out%20of%20several%20input%20videos (Zugriff am 08.03.2016 um 16:07).