Parallel- und Reihenstromkreise unter Last
Handys, Computer, Internet, Nervenimpulse, Herzschläge, Haushaltsgeräte, Autos, Beleuchtung, Blitze und vieles mehr sind möglich auf Grund von Elektrizität. Verhält sich Elektrizität in allen verschiedenen Situationen individuell oder lässt sich Elektrizität in allen Fällen gleich beschreiben?
| Parallel- und Reihenstromkreise unter Last | |

| |
| Kurzbeschreibung | |
|---|---|
| Reihenschaltung, Parallelschaltung, Versuche zur Unterscheidung von Strom und Spannung, Spannungsteiler, Leistung am Lastwiderstand, Innenwiderstand | |
| Kategorien | |
| Elektrizitätslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek.I/II |
| Basiskonzept: | Wechselwirkung, System |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Schülerexperiment |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Niklas Sturm |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Stephan Pfeiler |
Inhaltsverzeichnis
- 1 Didaktischer Teil
- 2 Versuchsanleitung ( Reihen-, Parallelschaltung, Leistung am Lastwiderstand, phänomenologisch)
- 3 Versuchsanleitung (Reihen-, Parallelschaltung, Leistung am Lastwiderstand, quantitativ)
- 4 Versuchserweiterung mit Daten aus 3.2 oder 3.3
- 5 Sicherheitshinweise
- 6 Literatur
Didaktischer Teil
Schüler und Schülerinnen (SuS) sollen im Physik-Unterricht Physik im Ganzen erfahren. Dazu gehört, dass die SuS die Natur der Wissenschaft kennen lernen. Ein bedeutsames Werkzeug zur Beschreibung der physikalischen Wirklichkeit sind Modellvorstellungen. Im Physikunterricht bieten sich viele Möglichkeiten das Wesen von Modellvorstellungen zu thematisieren. Im Folgenden wird eine kurze Charakterisierung vom Wesen physikalischer Modelle und ein Überblick über ausgewählte Modelle gegeben.
Frühe erkenntnistheoretische Einsicht entwickelte Karl Popper im ersten Drittel des 20-ten Jahrhunderts in seiner Wissenschaftstheorie. Er vertritt die philosophische Strömung des kritischen Rationalismus. Er kam zu dem Schluss, dass weder Modelle, noch Theorien, noch Annahmen über die Wirklichkeit als logisch wahr angesehen werden können. Der Überlegung liegt zu Grunde, dass Modelle und Theorien immer nur mit den aktuell verfügbaren empirischen Daten verglichen werden können. Obwohl ein Modell oder eine Theorie mit allen Daten übereinstimmt, bedeutet das nicht, dass diese Modelle und Theorien in Zukunft auch noch mit allen empirischen Daten übereinstimmen müssen. Ein Beispiel aus der Vergangenheit ist zum Beispiel die Newton'sche Mechanik und die Galilei-Transformation. Beides konnte eine lange Zeit viele mechanische Probleme lösen, bis Einstein seine Relativitätstheorie entwickelte und Beispielsweise gekrümmte Lichtwege experimentell bestätigt wurden. Gekrümmte Lichtwege können zum Beispiel während einer Sonnenfinsternis beobachtet werden. Da die Sonne vom Mond verdunkelt wird, blendet die Sonne nicht mehr und es lassen sich Sterne am Rand der Sonne beobachten, die direkt hinter der Sonne liegen. Ab dann war klar, Newton's Theorie konnte nicht die endgültige Wahrheit sein. Selbes Prinzip lässt sich auf alle Modelle, Theorien und Annahmen über die Wirklichkeit anwenden, denn niemals wird klar sein, ob eventuell ein Experiment, dass eine Theorie, ein Modell oder Annahmen übe die Wirklichkeit als falsch aufdecken kann, noch nicht entdeckt wurde. Somit können Modelle, Theorien oder Annahmen über die Wirklichkeit wahr sein, wir werden nur nie wissen können, ob wir wahre Modelle, Theorien oder Annahmen über die Wirklichkeit gefunden haben. Daher ist eine Auffassung von Modellen abseits der Kategorien wahr und falsch sinnvoll. Dazu werden im folgenden Abschnitt neuere charakteristische Merkmale von physikalischen Modellen erläutert.
Physikalische Modelle bilden die physikalische Wirklichkeit nach und erlauben Untersuchungen der Wirklichkeit sowie Vorhersagen über die Zukunft der physikalischen Wirklichkeit. Dabei erfassen Modelle die Wirklichkeit oft nur aspekthaft und vernachlässigen für die Untersuchungen unwichtiges.
Beispielsweise existieren zwei grundverschiedene Modellvorstellungen zu dem physikalischen Phänomen Licht. Die bekannten Modelle beschreiben die Phänomene die mit der Strahlenoptik oder der Wellenoptik gefasst werden können. Beide Modelle sind unterschiedliche Abbildungen von physikalischem Licht, die unterschiedliche Aspekte berücksichtigen und vernachlässigen. Unter Zuhilfenahme der Strahlenoptik können Beispielsweise Linsensysteme auf Vergrößerung untersucht werden. In dem Modell spielen die Welleneigenschaften des Lichts keine Rolle. Daher ist die Strahlenoptik für andere Fragestellungen das Licht betreffend, wie beispielsweise Interferenzen (Bei Interesse siehe Beitrag von Tom Leonhardt, Vortrag am 01.12.2016.), auch untauglich. Hierfür wurde das Wellenmodell des Lichtes entworfen. Dieses Modell ist wiederum unfähig Linsensysteme zu analysieren. Beide Modelle sind zur Beschreibung gewisser Aspekte von physikalischem Licht von Interesse und anerkannt, trotzdem widersprechen sie sich in ihrer grundsätzlichen Auffassung der Lichtnatur. Diese Inkonsistenz ist typisch für Modelle, doch ist ein Modell, im Gegensatz zur einer physikalischen Theorie, nicht dazu verpflichtet physikalische Phänomene konsistent zu erklären. Vielmehr steht die Funktionalität und Zweckdienlichkeit von physikalischen Modellen im Vordergrund.
Genauso sind physikalische Modelle durch eine gewisse Ungenauigkeit charakterisiert. Zum Beispiel entstehen an dem Rand von Linsen oder wenn ausreichend kleine Linsen verwendet werden Beugungseffekte, die von der Wellennatur des Lichtes her rühren. Solche Ungenauigkeiten setzen Grenzen innerhalb der Abbildungsfähigkeit der Wirklichkeit von Modellen. Allerdings werden diese Ungenauigkeiten und Grenzen akzeptiert, solange die Modelle für die interessanten Aspekte physikalischer Phänomene Ergebnisse liefern, die ausreichend genau mit den empirischen Daten übereinstimmen.
In der E-Lehre wurden ebenso Modelle geschaffen. So kann ein elektrischer Stromkreis auch als ein Fluss von Elektronen durch den elektrischen Leiter verstanden werden. Auf makroskopischer Ebene taugt die Vorstellung Elektronen würden fließen, um das Ohm’sche Gesetzt, die Kirchhoff’schen Regeln und das Leistungsgesetzt zu verstehen. Somit kann ein Modell auch Aufschluss über die Struktur der Wirklichkeit geben, auch wenn wir Modelle nicht als wahr betrachten können.
Ein anderes Modell bildet die Elektronenflüssigkeit auf fließendes Wasser ab. Das Wassermodell nach Wagenschein beispielsweise konzentriert sich dabei nur auf den Aspekt des fließenden Stroms und vernachlässigt eine Abbildung der Spannung auf den Druck. Ein ausführlicheres Modell kann auch die Spannung abbilden. Hierbei wurde ein Modell eines Modells entworfen. Damit ist das Wassermodell nach Wagenschein und das erweitere Wassermodell, ein Modell des fließenden Elektronen Modells. Umgekehrt könnte das fließende Elektronen Modell als Abbild von fließendem Wasser aufgefasst werden.
(vgl. Bailer-Jones, Daniela M.[1] (2002) S.3,6)
Versuchsanleitung ( Reihen-, Parallelschaltung, Leistung am Lastwiderstand, phänomenologisch)
Ziel des Versuchs
Diese Versuchsreihe dient der Einführung von Strom und Spannung. Der letze Versuch liefert ein Argument warum Strom und Spannung unterschieden werden müssen und warum zusätzlich zum elektrischen Strom eine weitere physikalische Größe zur Beschreibung eines Stromkreises nötig wird.
Aufbau
Folgende Geräte und elektrischen Bauelemente werden benötigt:
- Spannungsquelle ~0-20V, genutzt: Voltcraft Labornetzgerät DIGI 40, 0...40V/5A
- 3 Leuchtmittel mit verschiedenen Warmwiderständen
- R_L1 = 20 Ohm / >6V (geringster Widerstand)
- R_L2 = 60 Ohm / >6V (Widerstand R_L2 ≈
R_G + R_M) - R_L3 = 120 Ohm / >12V (größter Widerstand)
- 7 Lampenfassungen
- Regelbarer Vorwiderstand R_V 0 - 100 Ohm / ca. 0,3A mit (50 +- 2% Ohm), ca. 0,3A
- mehrere Verbindungskabel
- eventuell ein Steckboard
Werden andere Lampen genutzt, müssen diese auf den Vorwiderstand abgestimmt werden,
Die Lampe an der Stelle R_L leuchtet am hellsten, wenn folgendes gilt:
Regelbare Spannungsquellen besitzen für diesen Versuchsaufbau einen Geräteinnenwiderstand R_G von ungefähr 0 Ohm. Batterien und Akkus besitzen einen Innenwiderstand von ca. 3 bis 10 Ohm.
Durchführung
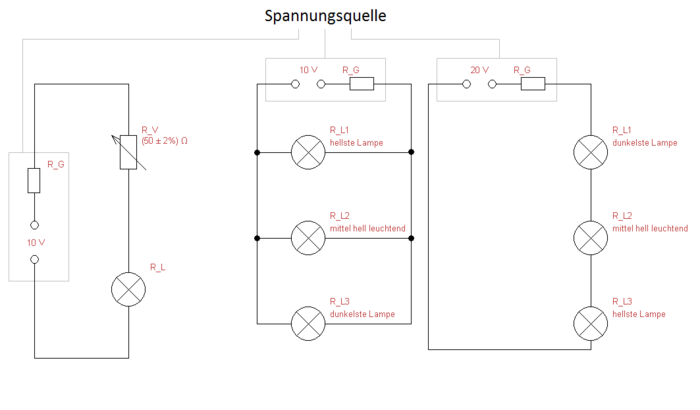
Stelle die Spannungsquelle auf 20 V ein. Schließe die Lampe R_L3 an die Spannungsquellean. Erweitere dann den Stromkreis um eine weitere in reihe geschaltete Lampe. Beobachte, die Lampe R_L3. Was stellst du fest? Wann beginnen die Lampen zu leuchten?
Schließe dann die letzte Lampe in reihe zu den anderen beiden Lampen an. Beobachte die beiden Lampen, die schon verschaltet sind. Was stellst du fest? Wann beginnen die Lampen zu leuchten?
Sortiere nun die Lampen nach ihrer Helligkeit. Die Dunkelste Lampe nennen wir R_L1, die mittel helle Lampe R_L2 und die hellste R_L3. Merke dir diese Reihenfolge und baue die Reihenschaltung auseinander.
Stelle die Spannungsquelle auf 10 V um. Schließe nun die Lampen parallel an die Spannungsquelle an. Beginne dabei mit der dunkelsten Lampe aus der Reihenschaltung, schließe danach die mittel hellste und dann die hellste Lampe an. Beobachte nach jeder neu angeschlossenen Lampe die zuvor schon angeschlossenen Lampen. Was stellst du fest? Wann beginnen die Lampen zu Leuchten?
Sortiere diese nach ihrer Helligkeit. Vergleiche die Reihenfolge von der dunkelsten Lampe zur Hellsten in der Parallelschaltung mit der Reihenfolge der Lampen von der dunkelsten Lampe zur Hellsten in der Reihenschaltung. Was stellst du fest?
Lasse die Parallelschaltung an die Spannungsquelle angeschlossen. Schließe zusätzlich den Widerstand R_V mit 50 Ohm Widerstand in reihe mit einer Lampenfassung an die Spannungsquelle an.
Stelle den Regelbaren Vorwiderstand R_V auf dem maximalen Widerstand ein. Drehe die dunkelste Lampe aus der Parallelschaltung, Lampe R_L3, in die Lampenfassung ein und verstelle den regelbaren Widerstand schrittweise von der maximalen Widerstandseinstellung runter zur minimalen Widerstandseinstellung. Was beobachtest du?
Schraube nun die Lampe R_L3 aus der Fassung und drehe sie wieder in die Fassung der Parallelschaltung ein. Stelle den regelbaren Widerstand R_V auf 50 Ohm ein. Schraube nun nacheinander, beginnend mit der dunkelsten Lampe der Parallelschaltung, die Lampen R_L3, R_L2 und R_L1 in die Lampenfassung von R_L ein, die in reihe mit dem regelbaren Vorwiderstand geschaltet ist. Wie leuchten die Lampen im Vergleich zueinander? Welche Lampe ist die Hellste?
<mediaplayer>File:Versuch2016.flv</mediaplayer>
Ergebnisse
Versuch: Reihenschaltung:
- Wird eine weitere Lampe hinzu geschaltet, so leuchten die schon angeschlossenen Lampen dunkler
- Alle Lampen Leuchten nur zusammen
- Alle Lampen gehen gleichzeitig an
- Die Lampen leuchten unterschiedlich hell
Versuch: Parallelschaltung:
- Angeschlossene Lampen leuchten, auch wenn andere Lampen noch nicht angeschlossen sind.
- Bezogen auf sich, leuchtet jede Lampe immer gleich hell. Keine Lampe wird dunkler, wenn eine weitere Lampe parallel geschaltet wird.
- Die 3 verschiedenen Lampen leuchten immer noch unterschiedlich hell. Aber im Vergleich zu der Reihenschaltung hat sich die Reihenfolge von der Dunkelsten zur hellsten Lampe umgekehrt. Im Vergleich zu der Reihenschaltung leuchtet nun die in der Reihenschaltung dunkelste Lampe in der Parallelschaltung am hellsten. Umgekehrt leuchtet in der Parallelschaltung die Lampe am dunkelsten, die in der Reihenschaltung am hellsten leuchtet.
Versuch: Reihenschaltung von einem regelbaren Vorwiderstand R_V mit der Lampe R_L3:
- Mit sinkendem Vorwiderstand steigt die Lampenhelligkeit.
Versuch: gleicher Vorwiderstand, aber unterschiedliche Lampen:
- Lampe R_L2 leuchtet in diesem Versuch am hellsten. In der Parallelschaltung und in der Reihenschaltung leuchtet Lampe R_L2 jeweils mittel hell.
- Lampe R_L3 und R_L1 leuchten deutlich schwächer als Lampe R_L2. In den Versuchen "Reihen- und Parallelschaltung" war jeweils eine der beiden Lampen die Hellste und die andre die Dunkelste.
Auswertung
Die Beobachtung an dem elektrischen Stromkreislauf lassen sich anschaulich in einem Wasserstromkreislauf interpretieren.
Dazu beschreibe ich in wenigen Sätzen ein Druckventil, das bei unserem Vergleich zwischen Wasser- und elektrischen Stromkreislauf dem Gegenstück einer Lampe entsprechen wird.
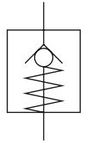
Das nächste Bild stellt anschaulich ein Ventil dar.
Die Linie, die oben aus der Box hinausragt symbolisiert den Wassereinlass. Dort wird zum Beispiel der Auslass einer Pumpe angeschlossen. Die gezackte Linie symbolisiert eine Feder, die eine Kugel gegen den Wassereinlass drückt. Die Feder soll gerade so lange sein, dass die Kugel den Einlass berührt. Wie weit die Feder zusammengedrückt und damit die Kugel den Einlass öffnet ist von dem Wasserdruck zwischen Einlass und Auslass abhängig. Ein großer Druckunterschied zwischen Einlass und Auslass drückt die Feder stärker zusammen, daher ist der Einlass auch weiter geöffnet und mehr Wasser strömt durch das Ventil. Vereinfacht dargestellt reibt dabei die Flüssigkeit auch mit größerer Kraft an der Kugel, wodurch die Kugel stärker aufgewärmt wird. Genauso kann die Kugel stärker aufgewärmt werden, wenn der Wasserstrom größer ist und das Wasser mit gleicher Kraft an der Kugel reibt.
Schalten wir nun viele, sehr kleine Ventile hintereinander, so können wir damit die Glühwendel einer Lampe in unserem Wasserstromkreislauf nachbilden. Die Reibungswärme die an den Kugeln entsteht entspricht dabei dem Leuchten der Glühwendel. Zur Vereinfachung stellen wir uns die Glühwendel aber nur als ein einziges Ventil vor. Das wird uns genügen. Zweitens legen wir fest, dass es keine offenen Rohre gibt. Das Wasser fließt also in einem Kreislauf durch die Pumpe oder gar nicht. (Der Korrektheit halber wird bemerkt, dass der Staudruck auch vernachlässigt wird, alle Rohrverbindungen den selben Querschnitt besitzen, kein Druck benötigt wird, um einen Wasserstrom durch ein Rohr zu treiben und der Wasserstrom turbulenzfrei fließt.)
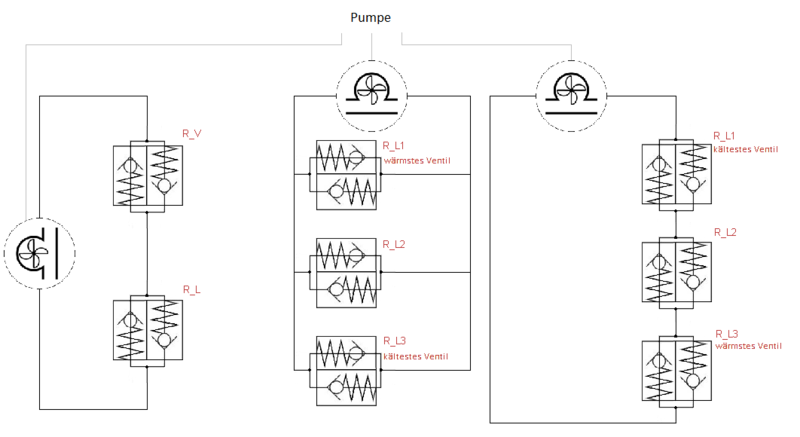
Nachdem wird nun das Ventil kennengelernt haben, stellen wir uns den elektrischen Stromkreislauf als Wasserkreislauf vor.
Dazu tauschen wird die Spannungsquelle mit einer Pumpe und die Lampe mit einem Ventil aus. In den 3 Ventilen sollen unterschiedlich „starke“ Federn eingebaut sein. Die Pumpe soll immer den gleichen Druck liefern. Wir schließen die 3 Ventile nacheinander an die Pumpe an. Da die Pumpe denselben Druck liefert, werden die Federn unterschiedlich weit eingedrückt. Wie oben beschrieben fließt, der Öffnung des Einlasses entsprechend, ein Wasserstrom durch das Ventil. Der größte Wasserstrom stellt sich durch das Ventil mit der schwächsten Feder ein. Umgekehrt stellt sich durch das Ventil mit der stärksten Feder der geringste Wasserstrom ein. Wie oben beschrieben ist die Erwärmung der Kugelventile, bei gleichem Druck, von dem Wasserstrom abhängig.
Im weiteren Versuchsverlauf hatten wir mehrerer Lampen in Reihe geschaltet. Wir beobachteten, dass die Lampe aus dem Versuch zuvor dunkler leuchtete, wenn weitere Lampen in Reihe geschaltet werden. Noch dazu stellten wir fest, dass die in Reihe geschalteten Lampen unterschiedlich hell leuchteten. Wie kann uns das Wasserstrommodell helfen, unsere Beobachtungen zu verstehen?
Betrachten wir nun eine Reihenschaltung mit 2 Ventilen. In einer Reihenschaltung fließt durch alle Rohre, alle Ventile und die Pumpe der gleiche Wasserstrom. Das heißt die Ventile sind alle gleich geöffnet. Da aber in die unterschiedlichen Ventile unterschiedlich starke Federn eingebaut sind, muss zwischen Ein- und Auslass der 2 Ventile ein Unterschiedlicher Druck herrschen. An dem Ventil, welches den größten Druckunterschied zwischen Ein- und Auslass aufweist, wird der Wasserstrom auch mit größter Kraft an der Kugel reiben und die Kugel im Vergleich zu den anderen Ventilkugeln am meisten erwärmen. Wir können auch sagen dieses Ventil stellt dem Wasserstrom den größten Durchflusswiderstand entgegen. Der Durchflusswiderstand ist eine neue Ventilkenngröße und gibt also an, wie viel Druck zwischen Ventileinlass und Auslass benötigt wird, damit sich ein bestimmter Wasserstrom einstellt. Nach unserem Verständnis von Durchflusswiderstand, hat das Ventil mit der „stärksten“ Feder den größten Durchflusswiderstand und das Ventil mit der „schwächsten“ Feder den geringsten Durchflusswiderstand.
Damit können wir in unserem Wasserstrommodell verstehen, wieso die Ventile unterschiedlich Warm werden. Übersetzt in den elektrischen Stromkreislauf ist das die Antwort auf die Frage, warum die Lampen unterschiedlich hell leuchten.
Eine Beobachtung ist aber noch unerklärt. Warum leuchtet eine Lampe dunkler, wenn eine weite Lampe in den Wasserstromkreis in Reihe geschaltet wird? Wir stellen uns die Situation im Wassermodell vor.
Wir schalten also ein weiteres Ventil zu dem Ersten in Reihe. Damit ein Wasserstrom durch das 2-te Ventil fließen kann, muss ein Druckunterschied zwischen Ventil Ein- und Auslass herrschen. Genauso muss ein Druckunterschied zwischen Ventil Ein- und Auslass des ersten Ventils herrschen. Die Pumpe stellt aber immer noch denselben Druck zur Verfügung. Dieser gesamte Druck teilt sich auf beide Ventile auf. Damit sinkt der Druck am ersten Ventil im Vergleich zum vorherigen Aufbau. Weniger Druck bedeutet aber auch, dass sich der Einlass des ersten Ventils etwas schließt. Also fließt weniger Wasserstrom durch das erste Ventil und noch dazu mit weniger Druck. Also wird die Kugel des ersten Ventils im Vergleich zum vorherigen Aufbau weniger erwärmt.
Übersetz in unseren elektrischen Stromkreislauf deckt sich das weniger Erwärmen mit schwächerem Lampenleuchten.
Wir haben auch festgestellt, dass der Wasserstrom durch das erste Ventil, wegen des in Reihe schalten des 2-ten Ventils, abgenommen hat. In der Reihenschaltung ist der Wasserstrom aber überall gleich. Daher wurde der Wasserstrom in der gesamten Schaltung durch den zusätzlich in Reihe geschalteten Durchflusswiderstand gehemmt.
Wir halten fest:
- die Ventile erwärmen sich nur, wenn der Wasserkreislauf geschlossen ist. Wird ein Ventil entfernt müssen die restlichen Ventile wieder mit der Pumpe verbunden werden.
- durch jeden weiteren in die Reihenschaltung eingefügten Durchflusswiderstand bzw. Ventil wird der Wasserstrom weiter gehemmt.
- durch jeden weiteren in die Reihenschaltung eingefügten Durchflusswiderstand bzw. Ventil wird der gesamt Druck der Pumpe weiter aufgeteilt.
- die einzelnen Ventile in einer Reihenschaltung im Vergleich zu einer einzeln Schaltung werden sich weniger stark erwärmen, da Druck und Wasserstrom durch die Bauteile abnimmt.
- Die Ventile mit der stärksten Feder / dem größten Durchflusswiderstand erwärmen sich am stärksten
In Unserm Versuch konnten wird die analogen Phänomene zu den letzten beiden Punkte beobachten.
Wechseln wir nun zu dem Teil des Versuches, in dem die Lampen parallel verschaltet werden. Halten wir zuerst unsere Beobachtungen aus dem elektrischen Parallelstromkreis fest.
- Angeschlossene Lampen leuchten, auch wenn andere Lampen noch nicht angeschlossen sind.
- Bezogen auf sich, leuchtet jede Lampe immer gleich hell. Keine Lampe wird dunkler, wenn eine weitere Lampe parallel geschaltet wird.
- Die 3 verschiedenen Lampen leuchten immer noch unterschiedlich hell. Aber im Vergleich zu der Reihenschaltung hat sich die Reihenfolge von dunkelsten zur hellsten Lampe umgekehrt. Im Vergleich zu der Reihenschaltung leuchtet nun die in der Reihenschaltung dunkelste Lampe in der Parallelschaltung am hellsten. Umgekehrt leuchtet in der Parallelschaltung die Lampe am dunkelsten, die in der Reihenschaltung am hellsten leuchtet.
Wie erklären wir uns diese Beobachtungen im Wasserstromkreis?
Der erste Punkt ins Wassermodell übersetzt besagt, dass Ventile nicht neu mit der Pumpe verbunden werden müssen, wenn ein anderes Ventil aus der Parallelschaltung entfernt wird. Im Wasserkreislauf ist diese Einsicht klar und der Leser frag sich eventuell, warum diese Erklärung an dieser Stelle erwähnt wird. Die Erwähnung ist wichtig, weil diese Erklärung im elektrischen Stromkreis, den wir anhand des Wassermodells verstehen wollen, nicht einfach klar ist. Dazu ist diese Tatsache der entscheidende Unterschied zwischen Parallel- und Reihenschaltung.
Wir erkennen auch, dass die Ventile direkt mit der Pumpe verbunden sind und der gesamte Pumpendruck zwischen Ventil Ein- und Auslass ansteht. Daran ändert sich nichts, wenn ein Ventil entfernt wird. Damit bleiben der Druck und der Wasserstrom durch ein Ventil auch unverändert unabhängig davon ob ein weiteres Ventil angeschlossen ist oder auch nicht. Was wiederum übersetzt ins Wasserstromkreismodell die Erklärung für die zweite Beobachtung ist. Denn bleiben Druck über ein Ventil und der Strom durch ein Ventil gleich, so reibt das Wasser auch gleich an der Ventilkugel und erwärmt diese gleich. Übersetzt ins elektrische Stromkreismodell ist das unsere zweite Beobachtung.
Wegen jedem weiteren Ventil wird aber auch ein neues Rohr stromdurchflossen. Da alle Ströme durch die Pumpe fließen, wird mit jedem weiteren Ventil der Wasserstrom durch die Pumpe ansteigen.
Aber warum kehrt sich die Reihenfolge von der Dunkelsten zur hellsten Lampe im Vergleich zur Reihenschaltung um?
Betrachten wir dazu die hellste und die dunkelste Lampe in der Reihenschaltung. In unserem Wassermodell entsprechen diese Lampen den Ventilen mit dem größten Durchflusswiderstand und dem geringsten Durchflusswiderstand. Schalten wir diese Ventile nun parallel. Da in einer Parallelschaltung zwischen Einlass und Auslass beider Ventile derselbe Druck ansteht, wird durch das Ventil mit dem größeren Durchflusswiderstand weniger Strom fließen. Daher wird sich das Ventil mit dem größeren Durchflusswiderstand weniger erwärmen, als das Ventil mit dem geringeren Durchflusswiderstand. In der Reihenschaltung hat sich allerdings wegen zuvor genannten Gründen das Ventil mit dem größeren Durchflusswiderstand stärker erwärmt. Die Reihenfolge vom am schwächsten erwärmten Ventil zum am stärksten erwärmten Ventil ist also in Parallel- und Reihenschaltung genau umgekehrt. Übersetzt in den elektrischen Stromkreislauf heißt das die Reihenfolge von dunkelsten zur hellsten Lampe ist genau umgekehrt in Parallel- und Reihenschaltung.
Wir halten fest:
- in einer Parallelschaltung sind alle Ventile direkt an die Pumpe angeschlossen.
- in einer Parallelschaltung ist der Druckunterschied zwischen allen Ventil Ein- und Auslässen gleich.
- Der größte Wasserstrom fließt durch das Ventil mit dem geringsten Durchflusswiderstand.
- Der geringste Wasserstrom fließt durch das Ventil mit dem größten Durchflusswiderstand.
- Mit jedem weiteren Ventil wird ein neuer Wasserstromweg eröffnet und der Wasserstrom durch die Pumpe muss steigen.
- Die Ventile erwärmen sich umgekehrt zu ihren Durchflusswiderständen.
In Unserm Versuch konnten wird die analogen Phänomene zu dem ersten und letzten Punkt beobachten.
Kommen wir nun zu dem Versuch mit dem sinkenden Vorwiderstand R_V in Reihe geschaltet mit der Lampe R_L3. Wir beobachteten, dass mit sinkendem Vorwiderstand die Lampe heller leuchtet. Für eine Erklärung in unserem Wassermodell können wir entweder nur den Wasserstrom, nur den Druck oder beides zusammen betrachten. Betrachten wir nur den Wasserstrom, so wissen wir, dass durch den sinkenden Durchflusswiderstand des Vorgeschalteten Ventils R_V der Wasserstrom durch das Ventil R_L3 steigen muss. Damit steigt auch der Druck zwischen Ein- und Auslass des Ventils R_L3 und damit die Erwärmung des Ventils R_L3. Übersetzt in den elektrischen Stromkreislauf wird mit sinkendem Vorwiderstand R_V die Lampe R_L3 immer heller leuchten.
Betrachten wir nur den Druck, so wissen wir, dass durch den sinkenden Durchflusswiderstand des Vorgeschalteten Ventils R_V weniger Druck an diesem Ventil benötigt wird, um einen Wasserstrom durch das Ventil R_V zu treiben. Da die Pumpe zu jeder Zeit denselben Druck bereitstellt, wird daher mehr Druck zu Verfügung stehen um die Feder im Ventil R_L3 weiter zu stauchen. Dadurch fließt auch mehr Strom durch das Ventil R_L3. Somit steigt die Erwärmung an dem Ventil R_L3. Übersetzt in den elektrischen Stromkreislauf wird mit sinkendem Vorwiderstand R_V die Lampe R_L3 immer heller leuchten.
Die Beobachtungen an dem letzten Versuch lassen sich aber nur erklären, wenn wir Wasserstrom und Druck gleichzeitig betrachten. Dazu überlegen wir uns zuerst, was wir erwarteten, wenn wir nur den Wasserstrom oder nur den Druck betrachteten.
Betrachten wir nur den Wasserstrom. Das Ventil R_L3 ist das Ventil, mit dem größten Durchflusswiderstand. Dieses Ventil schalten wir zuerst in die Reihenschaltung. Danach das Ventil R_L2 und danach das Ventil R_L1 mit dem geringsten Durchflusswiderstand. In diesem Versuch senken wir also den Durchflusswiderstand des Ventils R_L. Nach unserem ersten Versuch zur Reihenschaltung sollten wir vermuten, dass der Wasserstromfluss durch das Ventil R_L immer weiter ansteigt. Damit sollte die Erwärmung des Ventils R_L immer weiter ansteigen. Übersetzt in unseren elektrischen Stromkreis sollten wir also eine immer heller werdende Lampe vermuten. Das ist noch Widersprüchlich zu unsern Beobachtungen.
Betrachten wir nur den Druck, wird sich auch ein Widerspruch ergeben. Denn mit sinkendem Durchflusswiderstand R_L sollte ein immer niedriger Druck zwischen Ein- und Auslass des Ventils R_L nötig sein, damit ein Wasserstrom fließt. Demnach reibt das Wasser mit weniger Druck an der Ventilkugel und folglich sollte sich das Ventil immer weniger erwärmen. Übersetzt in unseren elektrischen Stromkreis sollten wir also eine abnehmende Helligkeit der Lampe R_L vermuten. Das Widerspricht allerdings auch unseren Beobachtungen.
Was in der Realität wirklich in unserem Wassermodell passiert, ist eine Überlagerung beider Überlegungen. Der Wasserstrom durch das Ventil R_L steigt und gleichzeitig sinkt der Druck zwischen Ein- und Auslass des Ventils R_L.
Betrachten wird zum besseren Verständnis zwei besondere Durchflusswiderstände für das Ventil R_L. Das Ventil R_L soll einmal keinen Durchflusswiderstand aufweisen. Nach unserer Definition des Durchflusswiderstandes bedeutet das, dass kein Druckunterschied zwischen Ventil Ein- und Auslass benötigt wird, damit ein Wasserstrom fließt. Das heißt, das Ventil enthält keine Feder und keine hinderliche Kugel. Unser Ventil ohne Durchflusswiderstand ist also ein Rohr.
Im anderen Fall soll unser Ventil einen "unendlich" großen Durchflusswiderstand besitzen. Ein "unendlich" großer Durchflusswiderstand entspricht in der Realität einer Sperre bzw. einem geschlossenem Rohr.
Für den Fall, dass unser Ventil R_L keinen Durchflusswiderstand besitzt würde kein Druck benötigt werden, um einen Wasserstrom durch das Ventil zu treiben. Folglich wird das Wasser auch ohne Druck durch das Ventil fließen. Somit würde das Wasser die Ventilkugel nicht durch Reibung erwärmen.
Für den anderen Fall eines "unendlich" großen Durchflusswiderstand versiegt der Wasserstrom und das Wasser kann auch nicht an der Ventilkugel reiben. Dadurch wird ebenso die Ventilkugel nicht erwärmt.
In unserer Vorstellung können wir das Ventil R_L1 mit dem geringsten Durchflusswiderstand als ein Ventil mit fast keinem Durchflusswiderstand betrachten und das Ventil R_L3 mit dem größten Durchflusswiderstand als ein Ventil, dass einen fast unendlich großen Durchflusswiderstand besitzt.
Schauen wir uns die einzelnen Ventile R_L3, R_L1 und R_L2 genauer an. Wenn wir das Ventil R_L3 mit dem größten Durchfluss Widerstand einbauen fließt ein geringer Wasserstrom, aber zwischen Ein- und Auslass am Ventil R_L3 stellt sich der größte Druckunterschied ein. Der höhere Druck an dem Ventil R_L3, der den Pumpendruck nicht übersteigen kann, überwiegt nicht den Effekt des geringeren Wasserstroms, welcher fast versiegt. Insgesamt erwärmt sich das Ventil R_L3 dadurch schwächer.
Bauen wir das Ventil R_L1 mit dem geringsten Durchflusswiderstand als das Ventil R_L ein, so ist fast kein Druckunterschied zwischen Ein- und Auslass des Ventils R_L1 nötig um einen beliebig großen Wasserstrom durch Ventil R_L1 zu treiben, aber das vorgeschaltete Ventil R_V begrenz den Wasserstrom trotzdem. Der durch das Ventil R_V begrenzte Wasserstrom durch das Ventil R_L1 überwiegt aber nicht den geringen Druckunterschied zwischen Ventil Ein- und Auslass am Ventil R_L1. Insgesamt erwärmt sich das Ventil R_L1 daher auch schwächer.
Am Ventil R_L2 halten sich dagegen beide Effekte die Waage, was insgesamt zur stärksten Erwärmung führt.
Übersetzt in unseren elektrischen Stromkreis wird also die Lampe R_L2 am hellsten leuchten.
Versuchsanleitung (Reihen-, Parallelschaltung, Leistung am Lastwiderstand, quantitativ)
Ziel des Versuchs
Der Versuch liefert ein Argument warum Strom und Spannung unterschieden werden müssen und warum zusätzlich zum elektrischen Strom eine weitere physikalische Größe zur Beschreibung eines Stromkreises nötig wird.
Würde die Leistung NUR proportional zum Strom (Fall 1) oder NUR proportional zur Spannung am Lastwiderstand (Fall 2) verhalten, also gäbe es nur eine der beiden physikalischen Größen, so würde im Fall 1 mit steigendem Lastwiderstand R_g die Leistung an R_g monoton abnehmen und im Fall 2 monoton zunehmen. Der Versuch widerlegt, dass nur einer der beiden Fälle alleine auftritt.
Versuch mit bekannten Lastwiderständen
Vorteil dieser Versuchsvariante
Abstände zwischen den Lastwiderständen sind genau festlegbar, wodurch leicht eine gleichmäßige Verteilung der Messpunkte erreicht werden kann.
Aufbau
Folgende Geräte und elektrischen Bauelemente werden benötigt:
- Spannungsquelle ~5-12V, genutzt: Voltcraft Labornetzgerät DIGI 40 0...40V/5A
- Vorwiderstand 5-40 Ohm / > 2 Watt, genutzt: (30 +- 2%) Ohm
- Regelbarer Widerstand 0 - 100 Ohm / ca. 0,3A ; genutzt wurden 2 in Reihe geschaltete regelbare Widerstande
mit 0-100 Ohm, 0-10 Ohm und jeweils 2% Unsicherheit
- 1 Voltmeter, genutzt: U_g wurde mit Metra Hit 18S gemessen
- mehrere Verbindungskabel
- eventuell ein Steckboard
Werden andere Widerstände genutzt, müssen diese auf den Vorwiderstand abgestimmt werden,
Das Leistungsmaximum am Lastwiderstand R_g stellt sich ein, wenn folgendes gilt:
Regelbare Spannungsquellen besitzen für diesen Versuchsaufbau einen Geräteinnenwiderstand R_G von ungefähr 0 Ohm. Batterien und Akkus besitzen einen Innenwiderstand von ca. 3 bis 10 Ohm.
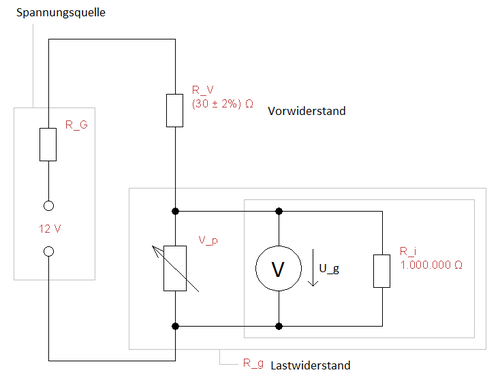
Durchführung
Baue den Stromkreis nach Plan auf und schließe die Messgeräte nach Plan an. Steigere den Lastwiderstand R_g, indem du den regelbaren Widerstand R_p in 1 Ohm oder 5 Ohm Schritten von dem kleinsten von 0 Ohm verschiedenen Wert auf den maximalen Wert änderst. Trage Leistung P_g am Lastwiderstand R_g in Abhängigkeit von den Lastwiderstand R_g in ein Koordinatensystem ein.
- ,da
Messunsicherheiten
Ergebnisse
Eine Excel-Datei mit den Originalmesswerten lässt sich hier downloaden.
Versuch mit bekannter Spannung am Vorwiderstand
Vorteil dieser Versuchsvariante
Diese Variante eignet sich für eine automatisierte Datenaufnahme mit einem Messwerteerfassungssystem. Dadurch können die Messwerte schneller aufgenommen und live in Form eines Funktionsgraphen veranschaulicht werden.
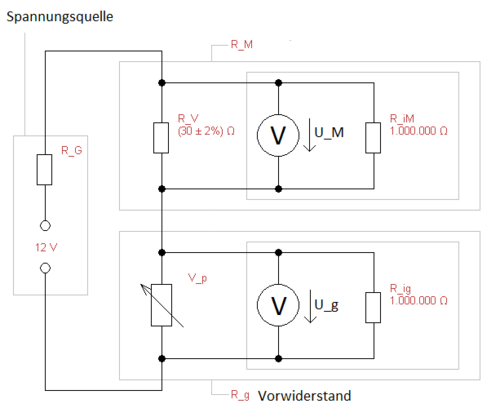
Aufbau
Folgende Geräte und elektrischen Bauelemente werden benötigt:
- Spannungsquelle ~5-12V, genutzt: Voltcraft Labornetzgerät DIGI 40 0...40V/5A
- Vorwiderstand 5-40 Ohm / > 2 Watt, genutzt: (30 +- 2%) Ohm
- Regelbarer Widerstand 0 - 100 Ohm / ca. 0,3A ; genutzt: 0-100 Ohm und 0-10 Ohm mit 2% Unsicherheit in Reihe geschaltet
- 2 Voltmeter, genutzt: U_g wurde mit Metra Hit 18S und U_M mit PeakTech 3335 DMM gemessen
- mehrere Verbindungskabel
- eventuell ein Steckboard
Werden andere Widerstände genutzt, müssen diese auf den Vorwiderstand abgestimmt werden,
Das Leistungsmaximum am Lastwiderstand R_g stellt sich ein, wenn folgendes gilt:
Regelbare Spannungsquellen besitzen für diesen Versuchsaufbau einen Geräteinnenwiderstand R_G von ungefähr 0 Ohm. Batterien und Akkus besitzen einen Innenwiderstand von ca. 3 bis 10 Ohm.
Durchführung
Baue den Stromkreis nach Plan auf und schließe die Messgeräte nach Plan an. Steigere den Lastwiderstand R_g, indem du den regelbaren Widerstand R_p in 1 Ohm oder 5 Ohm Schritten von dem kleinsten von 0 Ohm verschiedenen Wert auf den maximalen Wert änderst. Trage Leistung P_g am Lastwiderstand R_g in Abhängigkeit von den Lastwiderstand R_g in ein Koordinatensystem ein.
- ,da
Messunsicherheiten
Ergebnisse

Eine Excel-Datei mit den Originalmesswerten lässt sich hier downloaden.
Auswertung
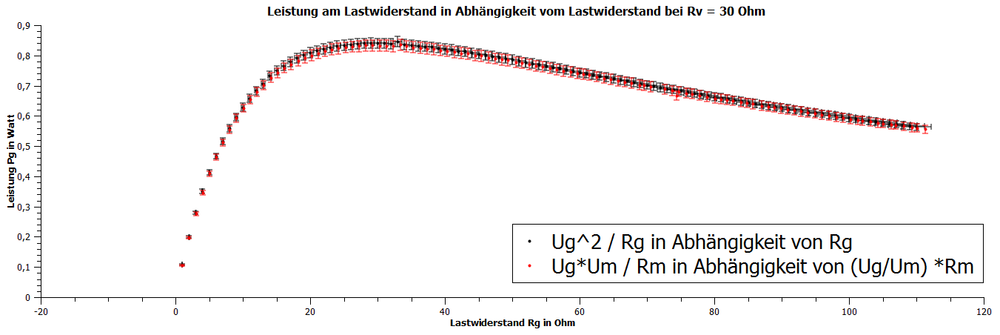
Erklären lässt sich dieses im Versuch dargestellte Phänomen nur dann, wenn Strom und Spannung als verschiedene voneinander abhängige physikalische Größen betrachtet werden. Solange eine der beiden Größen konstant gehalten wird muss die andere Größe proportional mit der an dem Lastwiderstand umgesetzten Leistung zusammenhängen. Unter dieser Voraussetzung führen die im ersten Absatz "Ziel des Versuches" implizit getroffenen und leicht experimentell darstellbaren Annahmen (geringerer Lastwiderstand führt zu größerem Strom durch den Lastwiderstand und zu geringerer Spannung am Lastwiderstand) zu einer Vorhersage, die auch im Versuch bestätigt werden kann.
Interpretation:
Für sehr kleine und kleiner werdende Lastwiderstände nähert sich die Spannung am Lastwiderstand 0V an und der Strom in der Reihenschaltung nähert sich einen vom Vorwiderstand abhängigen Maximalwert an. Da die Spannung bei konstantem Strom proportional zur Leistung ist, muss die Leistung sich ebenso 0W annähern.
Für sehr große und größer werdende Lastwiderstände nähert sich der Strom in der Reihenschaltung 0A an und die Spannung am Lastwiderstand nähert sich einer maximalen Spannung, der Quellspannung, immer näher an. Da der Strom bei konstanter Spannung proportional zur Leistung ist, muss die Leistung sich ebenso 0W annähern.
Zwischen sehr kleinen und sehr großen Lastwiderständen wird ein bestimmter Widerstand zu einer maximalen Leistung am Lastwiderstand führen.
Hinweise zu Versuchsabwandlungen
Was nicht funktionieren wird:
Anstelle der Lampen aus dem letzten Versuch der phänomenologischen Versuchsreihe könnte auch ein blanker glühender Draht genutzt werden. Der Drahtwiderstand lässt sich verringern, indem der stromdurchflossene Teil des Drahtes verkürzt wird. Dann wird der Effekt aber nicht sichtbar werden, denn die Temperatur des Drahtes und damit die subjektiv empfundene Helligkeit wird mit verkürzen des Drahtes monoton steigen. Um dies zu verstehen nehmen wir an der Draht sei ein schwarzer Strahler und der Draht gibt keine Wärmeenergie durch Konvektion oder Wärmeleitung an die Umgebung ab. D.h. der Draht strahlt die gesamte elektrische Energie über Wärmestrahlung ab.
Nach dem Stefan-Bolzmann-Gesetzt ist die abgestrahlte Leistung , wobei A die Drahtoberfläche und T die Drahttemperatur ist. Da die abgestrahlte Leistung gleich der elektrischen Leistung am Draht ist gilt:
, wobei r der Drahtradius und l die Drahtlänge ist.
Die Leistung pro Länge ist abhängig von Drahtwiderstand bzw. der Drahtlänge und steigt monoton mit kleiner werdendem Drahtwiderstand bzw. Drahtlänge:
,wobei falls und der spezifische Widerstand des Drahtes ist.
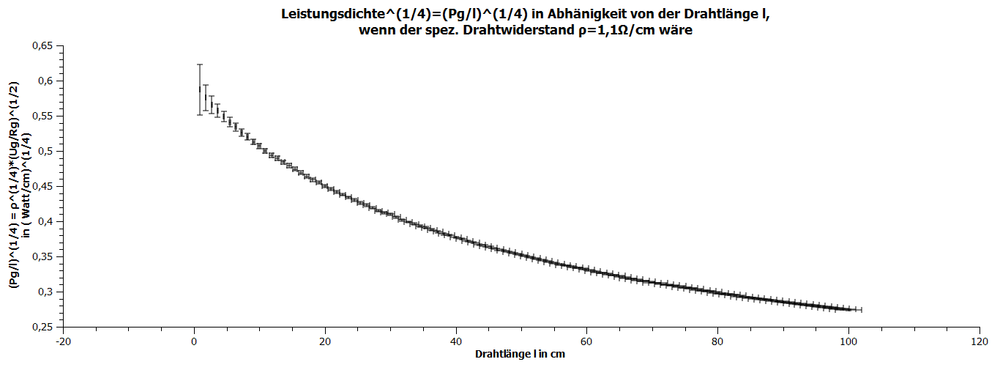
Damit steigt auch die Drahttemperatur und die subjektive Helligkeit des Drahtes an. Daher ist der Effekt nicht darstellbar.
Versuchserweiterung mit Daten aus 3.2 oder 3.3
Innenwiderstand einer Spannungsquellen mit Daten aus 3.2 (Praktische Relevanz: Leistungsabgabe einer Batterie)
Für den Versuch sollte als Spannungsquelle Batterien, Akkus oder jegliche Art von ungeregelten Spannungsquellen genutzt werden. Der Grund dafür ist, dass regelbare Spannungsquellen die Spannung an die Last anpassen. Zum Beispiel wurde in den Versuchen 3.2 und 3.3 die Last von 1 Ohm auf 110 Ohm abgesenkt (Leistung sinkt) und trotzdem fiel die Klemmspannung an der Spannungsquelle von 12V auf 10V. Das spricht für eine Spannungsregelung innerhalb der Spannungsquelle.
Aufbau
Lineare Regression
Da der Strom I in der Reihenschaltung überall gleich ist gilt:
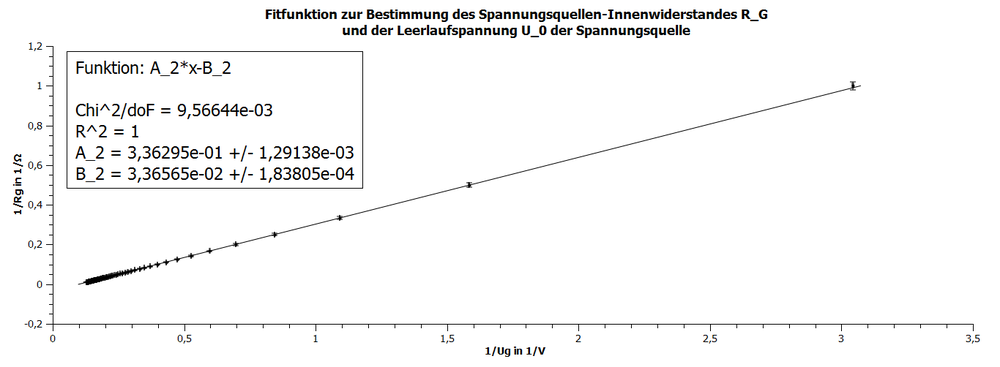
- . (Fitfunktion) ,wobei
- . (Fitfunktion) ,wobei
Der Geräte-Innenwiderstand der Spannungsquelle und die Leerlaufspannung kann mit linearer Regression aus den Koeffizienten folgendermaßen bestimmt werden :
Messunsicherheiten
- ,
- ,
Ergebnisse
Der Versuch mit den Daten aus 3.2 liefert einen Spannungsquellen-Innenwiderstand von und eine Leerlaufspannung von . Dafür wurde die mit 2 indizierte lineare Funktion verwendet, da hierdurch die Größe mit größeren relativen Unsicherheiten bei der Unsicherheitenbestimmung der Konstanten A und B berücksichtigt werden kann.
Innenwiderstand einer Spannungsquellen mit Daten aus 3.3 (Praktische Relevanz: Leistungsabgabe einer Batterie)
Aufbau
Lineare Regression
Da der Strom I in der Reihenschaltung ist überall gleich ist gilt:
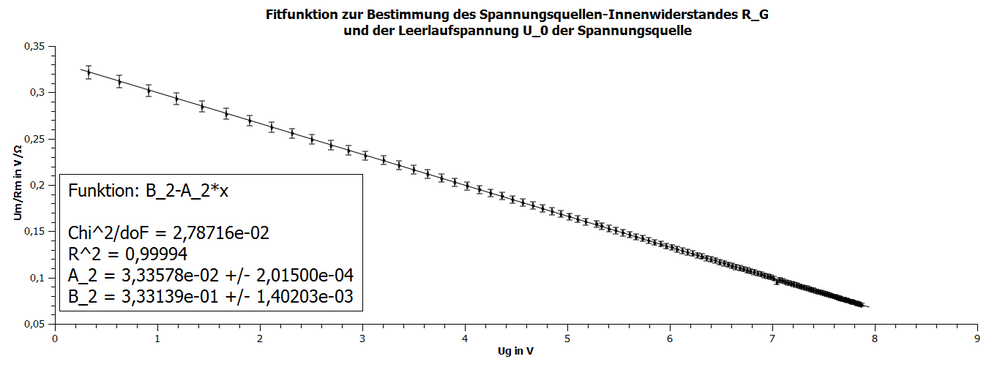
- . (Fitfunktion) ,wobei
- . (Fitfunktion) ,wobei
Der Geräte-Innenwiderstand der Spannungsquelle und die Leerlaufspannung kann mit linearer Regression aus den Koeffizienten folgendermaßen bestimmt werden :
Messunsicherheiten
Ergebnisse
Der Versuch mit den Daten aus 3.3 liefert einen Spannungsquellen-Innenwiderstand von und eine Leerlaufspannung von . Dafür wurde die mit 2 indizierte lineare Funktion verwendet, da hierdurch die Größe mit größeren relativen Unsicherheiten bei der Unsicherheitenbestimmung der Konstanten A und B berücksichtigt werden kann.
Auswertung
Da die verwendete regelbare Spannungsquelle die Klemmspannung der Last entsprechend anpasst, sind die Ergebnisse nicht der Realität entsprechend. Der Innenwiderstand und die Leerlaufspannung liegen möglicherweise auch außerhalb der angegebenen Unsicherheiten, da eben nicht, wie angenommen, die Leerlaufspannung und der Innenwiderstand über die dauer des Versuches konstant blieb.
Schlussfolgerungen aus diesem Versuch sind,
- dass eine Batterie, ein Akku oder eine andere Spannungsquelle mit konstanter Leerlaufspannung und konstantem Innenwiderstand genutzt werden muss.
- dass die Unsicherheit des Spannungsquellen-Innenwiderstandes hauptsächlich von der Unsicherheit des Vorwiderstandes abhängt.
Demnach sollte ein möglichst genau bestimmter Vorwiderstand genutzt werden.
Sicherheitshinweise
-maximale Leistung der Bauelemente einhalten
-maximaler elek. Strom durch Bauelemente einhalten
-maximale elek. Spannung an Bauelementen einhalten
Literatur
- ↑ Bailer-Jones, Daniela M. (2002): Naturwissenschaftliche Modelle: Von Epistemologie zu Ontologie; in A. Beckermann und C. Nimtz














![{\displaystyle T\approx {\sqrt[{4}]{\frac {P_{el}}{\sigma A}}}={\sqrt[{4}]{\frac {P_{el}}{\sigma 2\pi rl}}}={\sqrt[{4}]{\frac {1}{\sigma 2\pi r}}}{\sqrt[{4}]{\frac {P_{el}}{l}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f6596e5f15feb55db78e5d7b7493565ab3364ad)