Michelson-Interferometer
| Michelson-Interferometer | |
 Aufbau des Michelson-Interferometer | |
| Kurzbeschreibung | |
|---|---|
| Kohärentes Licht wird aufgespalten und anschließend, trotz unterschiedlicher Weglängen, zur Interferenz gebracht. | |
| Kategorien | |
| Optik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | System, Wechselwirkung, Energie oder Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel bis schwer |
| Informationen | |
| Name: | Franziska Tolksdorf |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Franz Boczianowski |
Durch das Aufteilen einer kohärenten Lichtquelle, hier ein He-Ne-Laserlicht, in zwei Teile, wird das Licht mit sich selbst zur Interferenz gebracht. Dafür durchlaufen die zwei Strahlen unterschiedlich weite Wege, um anschließend mit einer gewissen Phasendifferenz wieder überlagert zu werden. Mit Änderung der zu durchlaufenden Wegstrecke des zweiten Strahls, ändern sich auch die Phasendifferenzen und somit auch die Positionen der Interferenzmaxima. Anwendung findet das Michelson-Interferometer u.a. in der Astronomie.
Inhaltsverzeichnis
Didaktischer Teil
Das Michelson-Interferometer kann in der Sekundarstufe II im Rahmen der Wiederholung Licht - physikalisch gesehen behandelt werden (vgl. Rahmenlehrplan [1] (2006/2007), S. VIII). Diesem Experiment kann dabei ein besonderer Bildungswert zugesprochen werden. Zum einen zeigt es, dass eine kohärente Lichtquelle unter bestimmten Voraussetzungen mit sich selbst interferieren kann. Dabei kann zugleich auf die Vorkenntnisse der SchülerInnen aufgebaut werden, dass Licht an Grenzflächen transmittiert als auch reflektiert werden kann. Diese Eigenschaft wird in diesem Experiment ausgenutzt, um den Laserstrahl zu teilen und anschließend mit sich selbst interferieren zu lassen. Dadurch, dass ein Interferenzbild erzeugt werden kann, wird klar, dass die Wellenlänge weder durch Transmission noch durch Reflexion verändert wird, was eine Fehlvorstellung seitens der SchülerInnen sein könnte.
Besonders beeindruckend ist es, dass die Entstehung eines Interferenzbildes auf dem Schirm unabhängig von der Differenz der Weglängen der beiden Strahlen ist. Dabei entsteht je nach Justierung entweder das komplette Muster in Form von konzentrischen Kreisen oder nur ein Ausschnitt davon, welcher wie senkrechte Geraden aussieht. Durch die langsame Änderung der Position des Planspiegels in der Versuchsdurchführung (vgl. Kapitel Versuchsanleitung - Durchführung) und der damit verbundenen Änderung der Weglänge des transmittierten Laserstrahls, ändern sich die Positionen der Intensitätsmaxima innerhalb des Interferenzbildes, jedoch nicht die Position des Gesamtbildes auf dem Schirm. Somit zeigt dieses Experiment auf eindrucksvolle Weise und wie kein anderes, dass die Phasendifferenz zweier interferierender Strahlen abhängig von der Wegdifferenz und dem damit verbundenen Gangunterschied ist. Dieser sollte den SchülerInnen bereits aus der theoretischen Modelldarstellung der Interferenz bekannt sein. Wenn bei dem Experiment nur ein Ausschnitt des Interferenzmusters zu sehen ist, so ist zur Vermeidung von Fehlvorstellung zu klären, dass es sich dabei um Maxima höherer Ordnung handeln kann.
Neben der phänomenologischen Veranschaulichung eignet sich dieses Experiment bestens, um quantitative Messungen durchzuführen. Die Abhängigkeit des Gangunterschiedes von der Anzahl der Intensitätsmaxima und der Wellenlänge ist durch die Formel beschrieben, welche eine quantitative Untersuchung möglich macht (vgl. Kapitel Versuchsanleitung - Auswertung). Die Bestimmung der Wellenlänge der Laserquelle eignet sich hierbei besonders, da diese im nm-Bereich liegt und eine möglichst genaue Bestimmung dadurch sehr eindrucksvoll ist. Durch die Möglichkeit mit einem Interferometer Messungen durchzuführen, die sehr genau sind, kann im Schulunterricht auf die Anwendungsbereiche von Interferometern eingegangen werden. Diese liegen in der modernen Forschung u.a. in der Messung von Winkelgrößen von weit entfernten astronomischen Objekten (siehe [1] Uni Jena). Die Thematisierung der Anwendungsbereiche in der modernen Forschung von dem Experiment, welches im Unterricht durchgeführt wird, kann das Interesse seitens der SchülerInnen zusätzlich steigern. Zudem kann auch die Behandlung der Historie zur Steigerung des Interesses beitragen (siehe Michelson-Morley-Experiment).
Versuchsanleitung
Für diesen Versuch wird von der Firma Leybold ein komplettes Experimentierset angeboten, welches unter dem Versuch P5.3.4.2 angeboten wird (siehe [2] Leybold). Die einzelnen Artikelnummern von Leybold sind im Abschnitt Aufbau in Klammern notiert.
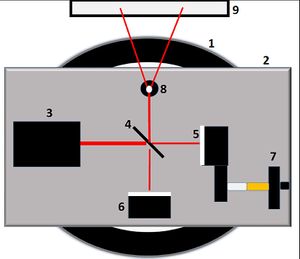
Aufbau
- 1: Reifen für Grundplatte (473 40)
- 2: Laseroptik-Grundplatte (473 40)
- 3: He-Ne-Laser, linear polarisiert (471 830), auf Laserträger (473 411)
- 4: Strahlteiler 50 % (473 432) in Halter für Strahlteiler (473 431) auf Optikfuß (473 421)
- 5: Planspiegel, feinjustierbar (473 461) auf Optikfuß (473 421) verbunden mit Feinstelltrieb (473 48)
- 6: Planspiegel, feinjustierbar (473 461) auf Optikfuß (473 421)
- 7: Untersetzungsgetriebe des Feinstelltriebs (473 48) auf Optikfuß (473 421)
- 8: Kugellinse f = 2,7 mm (473 471) auf Optikfuß (473 421)
- 9: Schirm, durchscheinend (441 53) auf Sockel (300 11)
Der Versuch wird in der Reihenfolge der oben genannten Nummerierung aufgebaut. Dabei ist darauf zu achten, dass der Strahlteiler 4 einen Winkel von 45° mit dem einfallenden Laserstrahl bildet. Der transmittierte Strahl soll den Planspiegel 5 etwa mittig treffen. Dieser wurde bereits vorher mit dem Feinstelltrieb 7 verbunden. Dabei soll die Verbindungsschraube (auf der Skizze die weiß-gelbe Verbindung) so eingestellt sein, dass eine Verschiebung nach rechts und links möglich ist. Eine ideale Justierung des Planspiegels liegt vor, wenn der vom Planspiegel reflektierte Strahl durch den Strahlteiler dicht neben der Laserquelle wieder auftrifft.
Der vom Strahlteiler reflektierte Strahl soll den Planspiegel 6 ebenso etwa mittig treffen.
Um den Laserstrahl aufzuweiten, sollen beide Strahlen, die durch den Strahlteiler 4 Richtung Schirm 9 laufen, durch die Kugellinse 8 hindurchlaufen. Dies erfordert in den meisten Fällen eine Nachjustierung der Planspiegel. Der Schirm 9 wird anschließend so aufgestellt, dass auf diesem das Interferenzmuster sichtbar ist.
Durchführung
Um die Phasenverschiebung der beiden interferierenden Strahlen zu verändern, muss die Strecke zwischen dem Strahlteiler und dem Planspiegel mit verbundenem Untersetzungsgetriebe des Feinstelltriebs (vgl. Skizze ) verändert werden. Dies geschieht, indem die Einstellschraube im Uhrzeigersinn gedreht wird. Daraufhin setzt sich das Untersetzgetrieb in Bewegung. An einer aufgebrachten Scheibe lässt sich dabei überprüfen, wie weit sich das Untersetzungsgetriebe bereits gedreht hat (vgl. Bild rechts). Nun wird zunächst darauf geachtet, dass eine Umdrehung getätigt wird. Auf dem Schirm ist dabei ein Interferenzmuster sichtbar, welches sich mit Veränderung der Distanz zwischen Strahlteiler und Planspiegel bewegt. Als Ausgangspunkt wird sich bereits vor der Durchführung für ein Maximum entschieden und gegebenenfalls an dieser Stelle auf dem Schirm eine Markierung angebracht. Dies ermöglicht eine bessere Übersichtlichkeit bei der anschließenden Abzählung von vorbeiziehenden Intensitätsmaxima. Bevor die Zählung beginnt, sollte mindestens eine Umdrehung bereits gedreht worden sein, da das Untersetzungsgetriebe am Anfang der Drehungen ein wenig haken kann und sich somit eventuell das Interferenzmuster auf dem Schirm anfangs nicht bewegt. Die Zählung kann beginnen, sobald sich das Interferenzmuster in einer konstanten Geschwindigkeit bewegt (vorausgesetzt die Einstellschraube wird in konstanter Geschwindigkeit gedreht). Die Anzahl der vorbeiziehenden Intensitätsmaxima auf dem Schirm wird nun abgezählt. Dies erfordert eine besondere Konzentration, da gleichzeitig auf die Umdrehungsscheibe als auch auf den Schirm zu achten ist. Die geringe Breite der Intensitätsmaxima und -minima erschwert das korrekte Abzählen. Nach der ersten Umdrehung des Untersetzungsgetriebes wird sich die Anzahl der Intensitätsmaxima gemerkt, um anschließend ohne Unterbrechung die zweite Umdrehung zu vollziehen. Nach der zweiten Umdrehung werden die durchlaufenden Intensitätsmaxima nach einer sowie nach zwei Umdrehungen notiert.
Ergebnisse
Es wurden fünf Messungen mit je einer und zwei Umdrehungen des Untersetzungsgetriebes ( und ) durchgeführt, wobei die durchlaufenden Intensitätsmaxima ausgezählt wurden.
| Durchgang | ||
|---|---|---|
| 1 | 1 | 16 |
| 2 | 33 | |
| 2 | 1 | 16 |
| 2 | 32 | |
| 3 | 1 | 16 |
| 2 | 31 | |
| 4 | 1 | 15 |
| 2 | 31 | |
| 5 | 1 | 16 |
| 2 | 32 |
Auswertung
Grundlage zur Berechnung der Wellenlänge in diesem Versuch ist die sogenannten Zwei-Quellen-Interferenz. Nach dieser findet eine konstruktive Interferenz statt, wenn der Gangunterschied , welcher die Wegdifferenz zweier oder mehrerer kohärenter Wellen bezeichnet, gleich einem Vielfachen der Wellenlänge der Quelle ist (). Die Vielfache gibt dabei die Ordnung des Maximums an.
Da in diesem Versuch die Verschiebung des Planspiegels durch den Hin- und Rückweg des Strahls doppelt berücksichtigt werden muss, kann die Formel wie folgt umgeformt werden: (im Folgenden wird der Gangunterschied ausschließlich nur noch mit bezeichnet, um bei der Angabe der Unsicherheiten eine Verwechslung auszuschließen).
Durch die Bewegung des Interferenzmusters wird das Maximum 1. Ordnung zum Maximums 0. Ordnung usw., weshalb die durchlaufenden Maxima lediglich durchgezählt und die Gesamtanzahl anschließend mit bezeichnet werden kann:
Die Verschiebung ergibt sich laut Herstellerangabe aus dem Produkt der Anzahl der Umdrehungen des Untersetzungsgetriebes und ().
In der Auswertung werden Berechnungen durchgeführt, Graphen mit Fit-Funktionen präsentiert, Messunsicherheiten abgeschätzt, die Ergebnisse interpretiert, diskutiert und abschließend bewertet.
| Durchgang | [] | [] | [] | ||
|---|---|---|---|---|---|
| 1 | 1 | 5 | 16 | 625,0 | 40,0 |
| 2 | 10 | 33 | 606,1 | 18,8 | |
| 2 | 1 | 5 | 16 | 625,0 | 40,0 |
| 2 | 10 | 32 | 625,0 | 20,0 | |
| 3 | 1 | 5 | 16 | 625,0 | 40,0 |
| 2 | 10 | 31 | 645,2 | 21,3 | |
| 4 | 1 | 5 | 15 | 666,7 | 45,4 |
| 2 | 10 | 31 | 645,2 | 21,3 | |
| 5 | 1 | 5 | 16 | 625,0 | 40,0 |
| 2 | 10 | 32 | 625,0 | 20,0 | |
| : Durchschnitt aller () | 631,3 | 10,3 | |||
| : Durchschnitt für () | 633,3 | 18,4 | |||
| : Durchschnitt für () | 629,3 | 9,1 | |||
| Herstellerangabe | 632,8 | kA | |||
Messunsicherheiten
Die Messunsicherheiten wurden für und wie folgt abgeschätzt:
- (dies ergibt sich aus einer geschätzten Abweichung von 5°)
Daraus ergab sich für die jeweilige Messunsicherheit durch das lineare Fortpflanzungsgesetz:
Durchschnitt
Zum einen wurde der Durchschnitt aller ermittelten Wellenlängen gebildet, unabhängig davon, wie groß die Gesamtverschiebung des Planspiegels war. Daher wurde aus n=10 Werten ein Durchschnitt ermittelt. Zum anderen wurde nach der Gesamtverschiebung unterschieden (vgl. Tabelle). Dafür wurde jeweils aus n=5 Werten ein Durchschnitt ermittelt. Für die Unterscheidung zwischen den Werten wurde sich entschieden, da die abgezählten Intensitätsmaxima innerhalb der Durchläufe abhängig voneinander sind und es damit fragwürdig wird, ob ein Mittel aller ermittelten Wellenlängen in diesem Fall wirklich sinnvoll erscheint.
In allen Fällen wurde der Fehler nach folgender Formel ermittelt:
Fazit
Betrachtet man die Unsicherheiten, so ist auffällig, dass diese im Allgemeinen recht hoch ausfallen. Dies liegt vor allem an der hohen Unsicherheit von . Bei der Zählung der Intensitätsmaxima kann sich aufgrund der Größe schnell verzählt werden, weshalb diese Unsicherheit in diesem Fall realistisch ist. Würde eine zweite Person die Maxima auszählen und die erste Person sich ausschließlich auf die Umdrehung konzentrieren, so wäre eine Reduzierung dieser Unsicherheit gewiss auf möglich. Beim Vergleich der drei Durchschnittswerte unteinander ist auffällig, dass der Durchschnitt die geringste Unsicherheit aufweist. Dies liegt vor allem daran, dass es sich hierbei um die Wellenlängen handelt, die aus der Auszählung von zwei Umdrehungen hervorgingen. Dabei wurden logischerweise etwa doppelt so viele Intensitätsmaxima ausgezählt, wie bei nur einer Umdrehung, was den Fehler der berechneten Wellenlänge reduziert. Alle drei Durchschnitte , und liegen so nah an der Herstellerangabe, dass es scheinbar nicht von Relevanz ist, wie der Durchschnitt gebildet wird.
Für den Schulalltag ist es sinnvoll nur eine Messung mit einer Umdrehung und mit zwei Umdrehungen durchzuführen. Dafür muss anschließend kein Durchschnitt ermittelt werden, sondern die beiden ausgerechneten Wellenlängen können einander gegenüber gestellt werden. Nur eine Messung heißt zwar auch ein ungenaueres Ergebnis mit höheren Fehlern, jedoch ist an den Messwerten zu erkennen, dass fast alle Einzelmessungen innerhalb ihrer Fehler mit der Herstellerangabe übereinstimmen, was im -Bereich bereits beeindruckend genug ist.
Sicherheitshinweise
- Nie direkt in den Laserstrahl schauen.
- Weiterhin ist darauf zu achten, dass alle spiegelnden Gegenstände im Raum abgedeckt sind, damit der Laserstrahl nicht unbeachtet gespiegelt wird.
- Die Planspiegel sowie der Strahlteiler sollten nie mit den Fingern direkt angefasst werden, da dies anschließend den Strahlengang beeinflussen kann.
Literatur
- ↑ Senatsverwaltung für Bildung, Jugend und Sport Berlin (2006/2007): Rahmenlehrplan für die gymnasiale Oberstufe - Physik; Senat Berlin, verfügbar unter Senat Berlin [16.04.2016]
Siehe auch
- Uni Jena: Interferometrie in der Astronomie; http://www.astro.uni-jena.de/Teaching/Praktikum/pra2002/node102.html [16.04.2016]
- Leybold: Bestimmung der Wellenlänge eines He-Ne-Lasers mit einem Michelson-Interferometer; http://www.leybold-shop.de/physik/versuche-sek-ii-universitaet/optik/wellenoptik/michelson-interferometer/bestimmung-der-wellenlaenge-eines-he-ne-lasers-mit-einem-michelson-interferometer/vp5-3-4-2.html [12.04.2016]