Chaos mit dem Pohlpendel

Chaos mit dem Pohlpendel
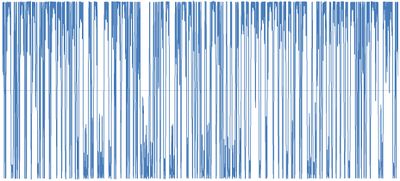
Pohlpendel mit resultierendem Graphen der x-Positionen
Kurzbeschreibung
Mit dem Pohlpendel werden Eigenschaften aus der Chaosphysik gezeigt.
Kategorien
Mechanik
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	Chaosphysik
Sonstiges
Durchführungsform	Lehrerdemoexperiment
Anzahl Experimente in dieser Unterkategorie	1, 2, 3
Anspruch des Aufbaus	mittel
Informationen
Name:	Elisa Kagelmaker
Kontakt:	${\text{kagelmae}}$@${\text{physik.hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Johannes Schulz

Das Pohlpendel ist für verschiedenste Schwingungen geeignet. Man kann freie Schwingungen mit und ohne Dämpfung zeigen, Schwingungen anregen und angeregte Schwingungen dämpfen. Beispielsweise lässt sich daran das Prinzip der Resonanz zeigen, wie in einem anderen Wiki-Artikel beschrieben.

Erweitert man das Pendel mit Zusatzmassen, so lassen sich auch Phänomene der Chaosphysik recht eindrucksvoll zeigen.

Didaktischer Teil

Chaosphysik und allgemein nichtlineare Physik sind kein Pflichtteil im Schulunterricht. Allerdings gibt es in der Sek II das Wahlthema „Nichtlineare Physik, Chaosphysik“. In diesem Modul lässt sich dieses Experiment durchführen, um Aspekte der Chaosphysik zu zeigen. Mehr dazu wird im Teil Auswertung ausgeführt.

Voraussetzungen sind die Kenntnisse zu Schwingungen. Diese werden in der Doppeljahrgangsstufe 9/10 gewonnen, im Modul P6 „Schwingungen Fadenpendel/Schraubenfeder“. Hier kann man auch schon mit dem Pohlrad arbeiten, um dieses später für das Chaos zu erweitern.

Ein weiterer Erkenntnisgewinn durch dieses Experiment kann das qualitative Arbeiten sein. Es werden Graphen lediglich qualitativ ausgewertet, da dies für die zu zeigenden Eigenschaften völlig ausreichend ist. Außerdem ist chaotisches Verhalten in diesem Rahmen nicht sinnvoll quantifizierbar. Diese Erkenntnis kann für die Schüler einen anderen Blick auf die Physik bieten.

Versuchsanleitung

Benötigte Materialien

• Pohlsches Drehpendel – Leybold/PhyWe 34600
• Netzgerät zum Pohlpendel – Leybold/PhyWe 346012

• Kabel
• Voltmeter bis 24 Volt
• Klebeband
• Massestücke
• einfarbiger, heller Hintergrund
• Kamera
• Computer mit der Software

Benötigte Software

• Viana (siehe Anbieterwebseite)
• Datenverarbeitungssoftware, bspw. Excel

Aufbau und Anpassung

Abb. [1]: Aufbau des Pendels mit Zusatzmassen, Netzteil und Voltmeter

Das Pohlrad wird normal aufgebaut. Man benötigt hierbei das passende Netzgerät und verbindet den Motor damit und schließt außerdem ein Voltmeter an. Die Wirbelstrombremse wird in diesem Versuch nicht benötigt. Auf der Abbildung ist gut zu sehen, dass die Kabel vom Netzteil in die oberen Buchsen und die Kabel für das Voltmeter in die unteren Buchsen gesteckt werden.

Das Wichtigste nun sind die Zusatzmassen. Als praktikabel haben sich ca. 30 Gramm erwiesen, die auf Höhe des Zeigers befestigt werden. Für eine etwas gleichmäßigere Belastung kann man beispielsweise 10 Gramm vor und 20 Gramm hinter dem Rad mit Klebeband platzieren.

Die Masse ist gut gewählt, wenn sich zwei Ruhelagen links und rechts von der Ausgangslage ohne Massen finden lassen. Zum Testen das Rad sanft in eine Richtung auslenken. Wenn es dann eindeutig auf dieser Seite bleibt und dasselbe auch auf der anderen Seite geschieht, ist die Masse passend.

Durchführung

Zum Durchführen des Experiments das Netzteil einschalten und den Motor starten. Man sollte ihn nicht mit einer Spannung betreiben, die ohne zusätzliche Massen der Resonanzfrequenz entspricht. Dann kann es passieren, dass aus dem Chaos wieder eine harmonische Schwingung wird.

Die Motorleistung wird über die Rädchen auf dem Motor eingestellt. Diese sind beschriftet, eines ist für die Grobeinstellung, das andere für die Feineinstellung. Am Voltmeter kann man die Versorgungsspannung ablesen.

Wenn die Einstellung korrekt ist, dann schwingt das Pendel meist um eine der beiden neuen Gleichgewichtslagen und wechselt in unregelmäßigen Abständen die Seite. Dies kann man zunächst mit bloßem Auge beobachten. Die unpassenden Fälle, die auftreten können, sind das Schwingen auf nur einer Seite oder das Wechseln der Seiten ohne kleinere Schwingungen. In diesen Fällen muss die Motordrehung angepasst werden. Beim vorliegenden Pohlrad hat sich eine Versorgungsspannung von ca. 5,50V als praktikabel erwiesen.

In diesem Experiment wurde dann mit der Software Viana gearbeitet. Diese ermöglicht es, Videos auszuwerten und so viele Messwerte zu erfassen. An den Auslenkungsmarkierer wird deshalb ein farbiger Punkt angebracht. Dieser sollte eine möglichst verschiedene Farbe von allen umliegenden Objekten haben. Da Computer offenbar eine sehr andere Auffassung von „verschiedenfarbig“ als der Mensch haben (vielleicht liegt es auch am Aufnahmegerät), sollte man dies unbedingt mit kurzen Videos testen, bevor man lange Aufnahmen macht, die dann unbrauchbar sind. Für das benutzte Pohlrad hat sich Grün als gut erkennbar erwiesen (auch wenn ich das Rot viel hervorstechender fand).

Nun stellt man am besten einen weißen Hintergrund hinter das Pohlrad, um jegliche Störfarben zu minimieren. Außerdem ist eine gute Beleuchtung wichtig. Gute Deckenlampen sind aber auch schon ausreichend. Mit einem Stativ stellt man nun eine Kamera so auf, dass die Markierung in jeder Position erfassbar ist. Das Pohlrad wird mit der vorher ermittelten Motorfrequenz und den befestigten Zusatzmassen gestartet und man kann die Aufnahme starten.

Ergebnisse

Abb. [2]: Durch Viana erhaltener Graph der x-Bewegung des Pendels über ca. 20 Minuten

Die Videos werden dann mit Viana ausgewertet (Eine Anleitung dafür soll hier nicht erfolgen, das Programm ist relativ selbsterklärend). Der Mittelpunkt des Rades bietet sich als Nullpunkt der Koordinaten an. Man kann auch eine Länge eingeben, da es aber nur um eine quantitative und keine qualitative Auswertung geht, ist das nicht nötig. Dann lässt man das Video automatisch analysieren. Die gewonnenen Daten kann man als Excel-Datei speichern und auswerten.

Für ein 20-Minuten-Video beispielsweise ergeben sich mehr als 70000 Datensätze, die deshalb hier nicht aufgelistet werden können. Diese kann man dann graphisch darstellen, hier sind die x-Positionen über die Zeit aufgetragen.

Für die y-Positionen ergibt sich ein ähnlicher Graph. Man sollte beide Graphen zusammen betrachten, allerdings ist auch schon der Graph für die x-Positionen sehr aussagekräftig. Man erkennt den Wechsel der Seiten durch den Durchgang durch die x-Achse und die Schwingungen, die nur auf einer Seite stattfinden.

Auswertung

Abb. [3]: Ausschnitt des obigen Graphen

In der Physik bezeichnet man mit Chaos das deterministische Chaos. Stochastische Systeme sind nicht gemeint. Bei theoretisch unendlichen Bewegungen lässt sich Chaos mit den folgenden Eigenschaften definieren:

• Selbstähnlichkeit – man kommt nach einiger Zeit wieder beliebig dicht an die Anfangskonfiguration oder jede andere beliebige Konfiguration heran
• Überdeckend – man überstreicht mit der Zeit beliebig weit vom Anfangszustand entfernte Zustände
• Sensitivität bezüglich des Anfangszustands – trotz fast identischer Startbedingungen beobachtet man stark auseinanderlaufendes Verhalten

Dieser Versuch zeigt sehr überzeugend die Eigenschaft der Selbstähnlichkeit chaotischer Systeme. In der Grafik erkennt man dies durch sehr gleich aussehende Graphenverläufe. Vor allem die kleineren Schwingungen auf einer Seite sind immer wieder sichtbar und sehr ähnlich.

Außerdem ist die Sensitivität sichtbar, wenn sich aus sehr ähnlichen Zustanden sehr verschiedene Verläufe entwickeln. Hier kann man die selbstähnlichen Verläufe betrachten und feststellen, dass sich der weitere Graph sehr anders entwickelt.

Dafür kann man durch die entstandene Grafik scrollen (Am besten direkt in Excel und nicht als Bild, damit man Skalierungsmöglichkeiten hat). Eine ähnliche Grafik ergibt sich für die y-Positionen, dann kann man beide Graphen parallel betrachten und noch besser auswerten.

Die Messwerte und Graphen, die in diesem Experiment gewonnen wurden, können hier zur besseren Betrachtung heruntergeladen werden: Exceldatei mit Messdaten und Graphen

Weiterführendes

Mit dieser Methode lassen sich auch alle anderen Schwingungen des Pohlrades auswerten.

Andere Versuche zur Chaosphysik sind das Magnetpendel und das Doppelpendel.

Siehe auch

Pohlsches Drehpendel