Pohlsches Drehpendel
| Pohlsches Drehpendel | |
 Drehpendel (vollständig aufgebaut) | |
| Kurzbeschreibung | |
|---|---|
| Das Drehpendel nach Pohl ist anwendbar für die Untersuchung von Drehschwingungen niedriger Frequenz. In diesem Versuch wird es verwendet, um den Resonanzfall einer angeregten mechanischen Schwingung (mit und ohne Dämpfung) zu untersuchen. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek II |
| Basiskonzept: | Energie |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment oder Schülergruppenexperiment |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Alexander Bönke |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Franz Boczianowski |
Mechanische Schwingungen und ihre Resonanz spielen in verschiedenen Bereichen des Alltags eine Rolle. Sei es das Wackeln der Waschmaschine beim Schleudern mit ungünstigen Drehzahlen oder die Schaukel auf dem Spielplatz. Extreme Fälle von Resonanz in Systemen, die nicht ausreichend gedämpft sind, können zur sogenannten Resonanzkatastrophe führen. Diese kann sogar massive Objekte, wie große Gebäude oder Brücken, zum Einsturz bringen. Das folgende Experiment verwendet das Drehpendel nach Pohl, um die Resonanz eines schwingungsfähigen, extern angeregten Systems zu untersuchen. Es wird hierbei besonders das Verhalten bei verschiedenen Dämpfungen analysiert. Das Drehpendel nach Pohl ist auf Grund seiner hohen Genauigkeit bei vergleichsweise geringem Aufwand dafür besonders geeignet.
Inhaltsverzeichnis
Didaktischer Teil
Bildungswert des Experiments
Schwingungen begleiten alle Schülerinnen und Schüler im Alltag. Bereits im Kindesalter werden sie auf Schaukeln angeschoben. Sie verwenden Verkehrsmittel mit dröhnenden Motoren und benutzen Handys mit Vibrationsalarm. Obwohl diese Dinge die Schülerinnnen und Schülern täglich umgeben, nehmen sie sie allenfalls am Rande wahr. Im Bereich der Schwingungen unterscheidet man zwischen mechanischen (der periodischen Bewegung von Körpern) und elektromagnetischen (Verschiebung von Ladungen) Schwingungen. Zu letzteren gehören im Besonderen die elektromagnetischen Signale (Wellen) wie Rundfunk und Fernsehen. Die Existenz elektromagnetischer Schwingungen ist schwierig zu erkennen. Sie finden in der Regel auf submikroskopischer Ebene statt und können nicht mit bloßem Auge wahrgenommen werden. Die Aussage, dass es elektromagnetische Schwingungen gibt, führt allenfalls zu einem Wissenszuwachs, aber zu keinem echten Erkenntnisgewinn. Mechanische Schwingungen hingegen lassen sich einfacher und offensichtlicher experimentell realisieren. Gerade im Themenbereich der Resonanz, dem sich dieser Versuch widmet, gibt es zum Teil beeindruckende Beispiele aus dem Leben. In der physikalischen Forschung werden mechanische Schwingungen u.a. zur Spektralanalyse genutzt. Die Absorptionsspektren der einzelnen Atomsorten kommen durch die Schwingung der einzelnen Atome um ihre Ruhelage zustande.
Das Unglück der Tacoma-Brücke, bei dem eine Brücke durch Resonanz unwillentlich einstürzt, ist ein gutes Einstiegsbeispiel vor dem Drehpendelversuch. Zu finden ist das Video unter anderem auf YouTube. Den Schülerinnen und Schülern wird gezeigt, dass Vernachlässigung von physikalischen Gesetzmäßigkeiten ernste Konsequenzen haben kann. Niemand, der zum ersten Mal Stahlträger im Wind taumeln sieht, wird sich diesem Eindruck entziehen können.
Ziel des Experiments
Das Resonanzexperiment mit dem Drehpendel nach Pohl hat folgendes Hauptziel:
Es zeigt auf, dass die Resonanz, dessen Existenz nun qualitativ nachgewiesen wurde, nicht chaotisch sein muss. Sie lässt sich mathematisch modellieren und physikalisch simulieren. Durch das Wissen um die Steuerbarkeit von Resonanz können ungünstige Fälle von vermieden oder wünschenswerte Fälle erreicht werden.
Außerdem bietet die quantitative Messung von Resonanzkurven die Möglichkeit, die Schülerinnen und Schülern zu sorgfältigem wissenschaftliches Arbeiten hinzuführen. Es wird nicht nur ein Aspekt des Messens verwendet, sondern mehrere. Reaktionszeit spielt eine Rolle (Zeit stoppen) und es werden Messdaten indirekt gemessen (Proportionalitäten). Skalen, die sich in relativer Bewegung zur Messmarkierung befinden, sind im richtigen Winkel abzulesen (Parallaxe).
Der Versuch bietet zwar kaum direkt und klar erkennbare Messunsicherheiten, er erfordert und fördert jedoch das Mitdenken der Schülerinnen und Schüler bei der Differenzierung zwischen relevanten und vernachlässigbaren Unsicherheiten.
Versuchsanleitung
Das Drehpendel ist eine bereits vorgefertigte Apparatur und somit einfach im Aufbau, erfordert aber Geduld und Präzision bei der Messung.
Aufbau
Benötigte Materialien
1 x Drehpendel nach Pohl (Leybold ID 346 00)
1 x Netzgerät zum Drehpendel (Leybold ID 346 012)
2 x Kabelverbindung für Erregermotor
2 x Kabelverbindung für Wirbelstrombremse (bei verwendeter Dämpfung)
1 x reguläre Hausstromversorgung (240V Steckdose)
1 x Stoppuhr
oder
1 x Spannungsmessgerät
2 x Kabelverbindungen für Spannungsmessgerät
Zusammenbau
- sämtliche Regler in 'Aus'-Stellung bringen und Netzschalter ausschalten
- Kabelverbindung zum Erregermotor (Anschlüsse am Drehpendel sowie am Netzgerät s. Abb.2 rechts unten und Abb.3 oben) anschließen
- Kabelverbindung zur Wirbelstrombremse (Anschlüsse Am Drehpendel sowie am Netzgerät s. Abb.2 Mitte unten und Abb.4 Mitte) anschließen
- Verbinden des Netzgeräts mit der Stromversorgung (Steckdose)
- Bereitlegen von Stoppuhr und Messprotokoll
Das Gerät ist nun ausgeschaltet und betriebsbereit, sobald der Netzschalter umgelegt wird (s. Abb. 2 links unten).
Für den Versuch wird eine Stoppuhr zur Frequenzmessung genutzt, soll ein Spannungsmessgerät stattdessen verwendet werden, wird der Zusammenbau um folgenden Punkt ergänzt:
- Kabelverbindung zwischen Erregermotor und Spannungsmessgerät (Anschlüsse am Drehpendel Abb.3 unten, Anschlüsse am Messgerät je nach Messgerät) anschließen
Durchführung
Vor Beginn der Messreihen schaltet man das Gerät mittels des Netzschalters an. Eventuelle Abweichungen der Ablesemarkierungen von Nulllagen sind zu beachten und entweder im Vorfeld zu korrigieren oder bei der späteren Auswertungen zu berücksichtigen. Korrigiert werden kann die Abweichung durch Drehung an der Schubstange (s. Abb.6 unten).
Es gibt nun zwei weitere Vorgehensweisen für zwei verschiedene Experimente:
Demonstrationsversuch
Das Drehpendel wird durch die Lehrperson in Betrieb genommen (s. Abschnitt Messung). Ein Schattenwurf bietet sich hier an, um es für alle sichtbar zu machen. Es bietet sich die Wahl repräsentativer Frequenzen zur Demonstration an. Eine fern der Resonanzfrequenz, eine nahe der Resonanzfrequenz und eine möglichst auf dieser.
Die Schülerinnen und Schüler beschreiben nun das Verhalten des Pendels bei Anregung und können jegliche Beobachtung äußern, die sie machen.
Messung
Zunächst wird vor jeder Messreihe eine Dämpfung mittels des Reglers für die Wirbelstrombremse (s. Abb. 2 Mitte links) eingestellt. Für Messungen ohne Dämpfung entfällt dies selbstverständlich. Es bieten sich Dämpfungen zwischen 1 und 10 Volt an, da bei höheren Dämpfungen die Amplituden nur noch schwer ablesbar sind. Es sollten mindestens 3 verschiedene Dämpfungen gewählt werden (exklusive der Vergleichsmessung ohne Wirbelstrombremse), um die Auswertung zu erleichtern.
Mit den Reglern am Erregermotor (s. Abb. 5) wird schrittweise die Spannung des Erregermotors erhöht. Das Drehpendel wird nun angeregt und beginnt nach rechts und links zu schwingen. Die Erregerspannung sollte nicht einfach von der Nullstellung schrittweise erhöht werden. Eine gute Vorgehensweise ist die Findung der Resonanzfrequenz der entsprechenden Dämpfung mit dem Grob- und im Anschluss mit dem Feinregler. Die Resonanzfrequenz wurde dann gefunden, wenn die Amplitude des angeregten Pendels durch Verstellen der Regler am Erregermotor nicht weiter signifikant erhöht werden kann. Hierzu darf ruhig etwas mehr Zeit eingeplant werden. Die Schülerinnen und Schüler sollten für eine gute Auswertung nahe der Resonanzfrequenz Messwerte mit geringerem Abstand wählen als entfernt davon. Günstig sind Schritte von einem Viertel Skalenteil in der Nähe bzw. einem halben Skalenteil des Grobreglers weiter von der Resonanzfrequenz entfernt.
Es werden nacheinander für jede Reglerstellung zwei Messungen gemacht:
Für die Messung der Erregerfrequenz mit der Stoppuhr wird die Markierung am Antriebsrad verwendet (s. Abb. 6). Nach Einstellen einer Erregerspannung werden mehrere Umläufe gemessen (mind. 10, um Messunsicherheiten durch Streuung der Werte gering zu halten). Die daraus errechenbare Frequenz ist der erste Messwert des Paares.
Nachdem die Erregerfrequenz so bestimmt wurde, wird das anzuregende Pendel betrachtet. Ist schon eine stabile maximale Auslenkung auf der Skala ablesbar? Lesen die Schülerinnen und Schüler bereits ab, bevor das Pendel seine maximale Auslenkung erreicht hat, wird das die Resonanzkurve verfälschen. Ein Hinweis von Lehrerseite ist hier sinnvoll. Die maximale Amplitude zur jeweiligen Erregerfrequenz ist der zweite Messwert.
Man erhält so folgende Messwertpaare für die Auswertung:
- Erregerfrequenz (reziprok gemessen in Periodendauern)
- Amplitude des angeregten Pendels (direkte Messung)
Alternative Messung mit dem Spannungsmessgerät
Hier wird die Erregerfrequenz ebenfalls indirekt gemessen, und zwar am Spannungsmessgerät. Die Erregerfrequenz ist proportional zur Erregerspannung. Um die Erregerfrequenzen aus der Spannung auszurechnen, muss jedoch zusätzlich der Proportionalitätsfaktor bestimmt werden. Für dessen Ermittlung reicht aber eine Messung mit der Stoppuhr. Es muss also nur einmal auf 10+ Perioden gewartet und gestoppt werden. Anschließend gestaltet sich die Durchführung einfacher und schneller als jedes Mal mit der Stoppuhr zu messen.
Man erhält folgende Messwertpaare:
- Erregerfrequenz (proportional gemessen in Erregerspannung (Volt))
- Amplitude des angeregten Pendels (direkte Messung)
Nach der Durchführung besitzt man nun 1 & 3+ Wertetabellen zu verschiedenen Dämpfungen.
Ergebnisse
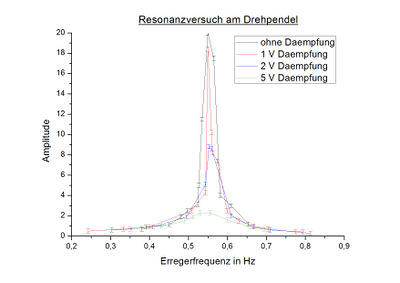
In einem Beispielexperiment wurden Messreihen mit einer Stoppuhr durchgeführt. Aufgenommen wurden 4 Messungen mit folgenden Dämpfungsstärken der Wirbelstrombremse:
- keine externe Dämpfung (Dämpfung 0 V)
- Dämpfung 1 V
- Dämpfung 2 V
- Dämpfung 5 V
Kein reales System ist vollständig ungedämpft, daher sollte bei der Diskussion der Ergebnisse betont werden, dass nur die zusätzliche Dämpfung durch die Wirbelstrombremse variiert wurde. Eine Resonanzüberhöhung (System gewinnt durch Anregung mehr Energie hinzu als es verliert) kann außerdem selbst mit einer Dämpfung auftreten.
Die Frequenzmessungen wurden über einen Zeitraum von 10 Periodendauern des Antriebsrades durchgeführt und entsprechend umgerechnet. Der Messfehler der Amplitudenmessung wurde auf Grund der Bewegung des Pendels auf ein Skalenteil (0,2) abgeschätzt.
Der Versuch lieferte folgende Ergebnisse:
Messwerte ohne externe Dämpfung
| Frequenz in Hz | Amplitude |
|---|---|
| 0,380 | 0,7 |
| 0,391 | 0,9 |
| 0,450 | 1,1 |
| 0,481 | 1,9 |
| 0,498 | 2,5 |
| 0,524 | 3,1 |
| 0,526 | 5 |
| 0,535 | 11,5 |
| 0,549 | 20 |
| 0,565 | 17,5 |
| 0,581 | 4 |
| 0,610 | 3 |
| 0,654 | 1,2 |
Messwerte mit 1 V Dämpfung
| Frequenz in Hz | Amplitude |
|---|---|
| 0,242 | 0,5 |
| 0,332 | 0,7 |
| 0,400 | 0,9 |
| 0,508 | 2,5 |
| 0,543 | 4,3 |
| 0,549 | 18,4 |
| 0,559 | 10,2 |
| 0,562 | 8,2 |
| 0,575 | 7,4 |
| 0,599 | 2,5 |
| 0,629 | 1,5 |
| 0,667 | 1 |
| 0,704 | 0,7 |
| 0,775 | 0,4 |
| 0,813 | 0,3 |
Messwerte mit 2 V Dämpfung
| Frequenz in Hz | Amplitude |
|---|---|
| 0,303 | 0,6 |
| 0,351 | 0,7 |
| 0,408 | 0,9 |
| 0,495 | 1,9 |
| 0,543 | 5,1 |
| 0,552 | 8,8 |
| 0,559 | 8,6 |
| 0,610 | 2 |
| 0,667 | 0,9 |
| 0,709 | 0,6 |
| 0,794 | 0,4 |
Messwerte mit 5 V Dämpfung
| Frequenz in Hz | Amplitude |
|---|---|
| 0,353 | 0,7 |
| 0,407 | 0,9 |
| 0,429 | 1 |
| 0,448 | 1,1 |
| 0,490 | 1,5 |
| 0,510 | 1,9 |
| 0,529 | 2,3 |
| 0,555 | 2,3 |
| 0,599 | 1,6 |
| 0,658 | 0,9 |
| 0,694 | 0,7 |
Zusätzliche Beobachtungen bei der Messung
Während der Durchführung der Messreihen oder bereits während des Demonstrationsversuchs können die Schülerinnen und Schüler außerdem Folgendes erkennen:
- Mit zunehmender Dämpfung nehmen die Amplituden generell ab. (Maxima ohne externe Dämpfung sind wesentlich höher als mit)
- Die Amplitude ohne externe Dämpfung erreicht als einzige den Maximalausschlag von 20 auf der Skala.
- Die tatsächliche Höhe des Maximalausschlags ist unbekannt, da das Pendel diesen abblockt (Metallblockade, zu hören durch ein Klacken bei Anschlag)
Für Schlussfolgerungen aus den Messwerten und Beobachtungen bietet sich eine grafische Darstellung der Ergebnisse an.
Auswertung
Verhalten bei allen Messungen
Es gibt einen klaren Peak (lokalen Hochpunkt) der Messwerte bei bzw. nahe der jeweiligen ermittelten Resonanzfrequenz.
Die gemessenen Resonanzfrequenzen (Maxima der Resonanzkurven in Abb.7) werden mit zunehmender externer Dämpfung außerdem geringer. Besonders auffällig ist das, wenn man die Kurve mit 1V Dämpfung sowie die Kurve zum Versuch mit 5V Dämpfung vergleicht. Es ist außerdem eine Linksverschiebung der Resonanzfrequenz zu höherer Dämpfung hin zu erkennen.
Dies geschieht, weil die Differenz zwischen zugeführter Energie und Energieverlust in Richtung der Resonanzfrequenzen der jeweiligen Systeme (ohne externe Dämpfung, mit 1 V, etc.) immer weiter abnimmt. Die Verlustleistungen bei der Übertragung sind bei der Resonanzfrequenz minimal.
Die Linien der einzelnen Dämpfungen kreuzen sich in der grafischen Darstellung. Das ergibt physikalisch keinen Sinn. Grund dafür sind die zu weit auseinanderliegend gewählten Messpunkte.
Verhalten ohne externe Dämpfung
Bei der Resonanzfrequenz nimmt das System stetig Energie auf, welches sich in einer stetig größer werdenden Amplitude des angeregten Pendels widerspiegelt. Das Geräusch, welches von der Metallblockade verursacht wird, kann hier verwendet werden, um die Schülerinnen und Schüler auf den Umstand hinzuweisen, dass der Ausschlag immer größer werden würde, wenn nicht gebremst. Eine ungebremste Resonanzüberhöhung hätte eine Zerstörung (Resonanzkatastrophe) des Aufbaus zur Folge.
Das bedeutet, dass in der Messung ohne externe Dämpfung die sogenannte Resonanzüberhöhung auftritt, d.h. die dem System nahe der Resonanzfrequenz pro Umlauf des Erregers zugeführte Energie ist größer als der Energieverlust durch die interne Dämpfung.
Die Schülerinnen und Schüler können auch folgende Formel zur Berechnung der internen Dämpfung verwenden :
Die Formel ergibt sich aus der Differentialgleichung des angetriebenen Pendels
Letztere ist jedoch für Schüler eher ungeeignet und könnte zur weiteren Forderung in besonders guten Kursen angesprochen und bearbeitet werden.
Verhalten bei externer Dämpfung
Die zugeführte Energie ist bei den durchgeführten Messungen nicht größer als die Verluste gewesen. Es gilt folgender Zusammenhang, wenn keine Resonanzüberhöhung auftritt.
Das Gleichgewicht zwischen zugeführter Energie und Verlust durch die Dämpfung sorgt dafür, dass die Amplitude bei diesen Messreihen konstant gehalten wird. Dies geschieht sogar bei der Resonanzfrequenz, denn solange die zugeführte Energie den Verlust nicht übersteigt, kann die Amplitude nicht weiter erhöht werden.
Die auftretende Phasenverschiebung von 0 weit links der Resonanzfrequenz über bei dieser bis hin zu weit rechts davon kann auch von Schülerinnen und Schülern bemerkt werden. Der Vergleich zum Anschieben der Schaukel zu bestimmten Zeitpunkten und dem jeweiligen Effekt bietet sich an, um das zu anschaulich zu erklären.
Messunsicherheiten
Messunsicherheiten bei quantitativen Versuchen wie diesem sollten auf jeden Fall spätestens in der Sek II thematisiert werden.
Für den Versuch wurde für die Amplitudenmessung eine Unsicherheit von einem Skalenteil (entspricht 0,2) angesetzt, da sich das Pendel ständig in Bewegung befand. Eine Messung mit Stoppuhr bringt besonders durch die Reaktionszeit Unsicherheiten mit sich. Da die Reaktionszeit aber in der Regel ähnlich groß ist (etwa 0.2 Sekunden später), ergibt sich ein doppelter Versatz in die gleiche Richtung beim Stoppen, einmal zu Beginn der Messung, einmal zum Ende. Die endgültige Unsicherheit durch menschliches Fehlverhalten ist also nur die wesentlich geringere Differenz dazwischen.
Der prozentuale Anteil der jeweiligen Unsicherheiten am Messwert kann und sollte von den Schülerinnen und Schülern rechnerisch ermittelt werden, um eine Einschätzung über den größten Fehler während des Versuchs vornehmen zu können. Hierzu eine relativ einfache Größtfehlerabschätzung:
Die maximale Auslenkung der Skala beträgt 20. Bei einem Ablesefehler von 0,2 sind dies 1% Abweichung. Mit abnehmder Amplitude noch weiter zunehmend. D.h.
Die Reaktionszeit liegt in der Regel bei ca. 0,2 Sekunden (s.o.). Gerade bei den noch jüngeren Schülerinnen und Schülern sollte sie höher ausfallen. Zieht man diese Spanne voneinander ab und nimmt eine Schwankung von ca. 0,05 s der Reaktionszeiten einer Einzelperson an, erhält man nach Differenz eine Unsicherheit von 0,1 s zwischen den Periodendauern. 10 Periodendauern sind in der Messung mindestens 12 Sekunden lang gewesen. Damit liegt die Ungenauigkeit der Erregerperiodendauer bei einem Wert, der auf jeden Fall kleiner als 1% ist, solange mind. 10 Perioden gemessen werden.
Die Unsicherheit der Zeitmessung für die Periodendauern ist also stets geringer als die der Amplitudenmessung. Zur Verringerung der Messunsicherheiten bieten sich die Erhöhung der gemessenen Periodenanzahl oder das mehrfache Ablesen der Amplituden an.
Abweichungen kleiner als 5% des Messwerts sind in der Schule bereits gute Werte!
Der Aufbau liefert in dieser Form also recht genaue Ergebnisse bei der Bestimmung von Resonanzkurven. Die Qualität der Kurven lässt sich durch feinere Messpunktverteilung leicht noch weiter verbessern.
Schlussfolgerungen
Es lassen sich folgende Punkte als Ergebnis des Versuchs festhalten:
- Ein Schwingungssystem, in dem die zugeführte Energie pro Schwingungsdauer die Verluste durch Reibung übersteigt, erlebt eine Resonanzüberhöhung, eine stetige Erhöhung der Schwingungsamplitude. Wird dieser Vorgang nicht gebremst, kommt es zur Resonanzkatastrophe.
- Je stärker ein Schwingungssystem gedämpft ist, desto geringer ist seine Resonanzfrequenz.
- Soll einem schwingungsfähigen System möglichst verlustfrei Energie zugeführt werden, sollte das nahe oder bei der Resonanzfrequenz stattfinden. Bei der Resonanzfrequenz sind die Dämpfungsverluste minimal (Reibung).
- Möchte man einem schwingungsfähigen System möglichst wenig Energie auf einmal zuführen, z.B. bei empfindlichen Bauteilen, sind Bereiche weiter entfernt von der Resonanzfrequenz zu wählen. Bei Bauwerken wie der Tacoma-Brücke löst man das Problem durch einsetzen von Bauteilen verschiedener Eigenfrequenzen. So schwingt niemals das ganze Bauwerk, höchstens einzelne Teile.
- Weit abseits der Resonanzfrequenz ändert sich die Amplitude kaum oder nur sehr schwach. Das ist z.B. hilfreich bei der Verwendung von Lautsprechern und Verstärkern.
- Will man ein schwingungsfähiges System wie eine Schaukel optimal anregen und kann die Frequenz nicht anpassen, ist eine Phasendifferenz von die beste Wahl.
Sicherheitshinweise
Es gelten die allgemeinen Regeln zum Umgang mit elektrischem Strom und Spannung.
Die maximal zulässige Spannung bei der Regelung der Wirbelstrombremse ist außerdem zu beachten. (Regler nicht auf Anschlag drehen)
Literatur
Bedienungsanleitungen Leybold :
Pendel: http://www.ld-didactic.de/ga/3/346/34600/34600d.pdf (letzter Aufruf: 27.10.2013 15:19 CET)
Netzteil: http://www.ld-didactic.de/ga/3/346/346012/346012d.pdf (letzter Aufruf: 27.10.2013 15:19 CET)
Theorie zur Resonanz:
Grehn, J.: Metzler Physik; 1992, 2. Auflage, Schroedel Schulbuchverlag, Hannover
Meschede, D.: Gerthsen Physik; 2010, 24. Auflage, Springer-Verlag, Berlin