Bestimmung der Lichtgeschwindigkeit mit kurzen Lichtimpulsen
| Bestimmung der Lichtgeschwindigkeit mit kurzen Lichtimpulsen | |
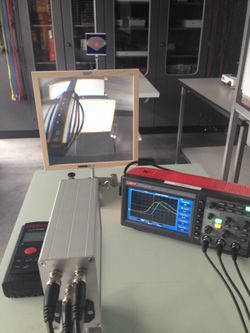
 Instrumente: Entfernungsmesser, Osziloskop und Grundeinheit | |
| Kurzbeschreibung | |
|---|---|
| Bestimmung der Lichtgeschwindigkeit durch elektronische Laufzeitmessung | |
| Kategorien | |
| Optik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | ab Kl. 7/8, ideal Kl. 9/10 |
| Basiskonzept: | System, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Schüler*innen-Experiment, Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Robby Büchner |
| Kontakt: | @ E-Mail] |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Daniel Zechlin |
Die Bestimmung der Lichtgeschwindigkeit kann auch historisch (Drehspiegelexperiment), sehr präzise (Lissajous-Figuren) oder mit Alltagsgeräten (Käse im Mikrowellenherd) durchgeführt werden. Die Vorzüge des hier verwendeten Experimentiersets der Firma MAPHY sind jedoch die geringen Anschaffungskosten und der vergleichsweise sehr einfache Aufbau. Kurze Lichtimpulse werden von einer LED ausgesendet. Ein Teilstrahl wird direkt nach dem Strahlteiler detektiert. Der andere legt eine gewisse Entfernung zurück, wird zum Strahlteiler zurückgeworfen und nach einer weiteren Reflexion an diesem ebenfalls detektiert. Durch die Zeitdifferenz der beiden Signale (erster Teilstrahl wird detektiert, zweiter Teilstrahl wird detektiert) und die Kenntnis der Entfernung zwischen Strahlteiler und Reflektor, lässt sich die Lichtgeschwindigkeit einfach bestimmen. In umgekehrter Logik (Lichtgeschwindigkeit bekannt, Entfernung gesucht) funktionieren in der Praxis Laser-Entfernungsmesser und Radarpistolen.
Inhaltsverzeichnis
Didaktischer Teil
In diesem Abschnitt soll der Bildungswert der Bestimmung der Lichtgeschwindigkeit im Unterricht erläutert werden. Für diese sogenannte didaktische Analyse schlägt W. Klafki [1] fünf Kriterien vor: Exemplarische Bedeutung, Gegenwartsbedeutung, Zukunftsbedeutung, innere Struktur des Themas und Zugänglichkeit. Der Schwerpunkt in diesem Artikel liegt auf der Gegenwarts- und Zukunftsbedeutung.
Zur exemplarischen Bedeutung sei deshalb nur gesagt, dass die Bestimmung der Lichtgeschwindigkeit mit kurzen Lichtimpulsen beispielhaft verdeutlicht, dass elektromagnetische Wellen und Informationen allgemein sich mit einer endlichen Geschwindigkeit ausbreiten.
Dieser Versuch verknüpf dabei zwei Konzepte, die die gegenwärtige Sicht von Schülerinnen und Schülern auf die Welt mitbestimmen:
a) Geschwindigkeit ist der Quotient aus zurückgelegter Strecke und der dabei vergangenen Zeit.
b) Schatten ist Abwesenheit von Licht - im Gegensatz zur Alltagsvorstellung, dass Licht und Schatten den gleichen Stellenwert haben. (vgl. [2] Vorlesung B. Priemer (2013))
Aus ihrer Erfahrungswelt ist Lernenden bereits bekannt, dass Licht sich ausbreitet. Beispielsweise kennen sie die Beobachtung, dass Sonnenlicht durch Öffnen eines Rollos von außen in einen Raum hinein dringen kann. Die Frage, ob das Licht dann sofort oder mit einer gewissen Verzögerung den Raum „ausleuchtet“ stellt sich wahrscheinlich nicht automatisch. Wird das Problem vom Lehrenden aufgeworfen, so sollte sich den Schülern die Methode zur Beantwortung der Frage jedoch schnell erschließen: Man misst in welcher Zeit das Licht eine bestimmte Strecke zurückgelegt hat. (siehe a) )
Das Ergebnis (d.h. die Endlichkeit der Lichtgeschwindigkeit) hat für die gegenwärtige Weltsicht der Lernenden beispielsweise folgende - im Sinne der pädagogischen Entwicklung wünschenswerte - Konsequenzen:
- Der Blick in den Sternenhimmel ist ein Blick in die Vergangenheit.
- Auch digitale Informationen können sich nicht unendlich schnell ausbreiten.
Sowohl Astronomie, als auch Computertechnik entsprechen erfahrungsgemäß dem Interesse vieler Schülerinnen und Schüler. Um zu zeigen, dass das Resultat des Versuchs wirklich Bedeutung für die Lebenswelt der Jugendlichen hat - zwei Beispiele:
- (Video)telefonate mit Freunden an weit entfernten Orten sind deutlich verzögert. Ein erheblicher Teil dieser Verzögerung resultiert direkt aus der begrenzten Geschwindigkeit der Signalausbreitung (mit Lichtgeschwindigkeit in Glasfaserkabeln z.B. 0,1 s für 9 000km Strecke von Berlin nach San Francisco und zurück)
- Die Geschwindigkeit von Micro-Prozessoren ist durch ihre Größe begrenzt. Während eines Rechenschrittes, eines sogenannten Taktes, müssen alle Signale alle Bereiche des Prozessors erreicht haben. Auf dem breiten Markt wurden in der Vergangenheit Prozessoren mit maximal 4GHz an Rechenschritten pro Sekunde verkauft. Der Grund wird schnell klar, wenn man berechnet, welche Strecke Licht im Vakuum in einer 4-milliardstel Sekunde bzw. einem Takt zurücklegt: Wenn man dazu noch bedenkt, dass die Lichtgeschwindigkeit in Materie deutlich geringer ist, so wird deutlich, dass Prozessoren mit mehreren cm Durchmesser nicht schneller getaktet sein können.
„Worin liegt [nun] die Bedeutung des Themas für die Zukunft der Kinder?“[1] Die angeführten Lebensweltbezüge im Jugendalter bilden die Grundlage für die Arbeit von Astronomen. Bruchteile von Sekunden bei der Datenübertragung spielen an globalen Aktienhandelsplätzen durchaus eine wichtige Rolle und die Bedeutung für Informatiker, Physiker, Ingenieure und zahlreiche technische Ausbildungsberufe wird sofort klar. Doch was ist mit den Schülerinnen und Schülern, die andere Berufe ergreifen? Auch diese werden wohlmöglich Laser-Entfernungsmesser beim Umzug benutzen oder bei Überhöhter Geschwindigkeit mit dem Auto nach der Messung einer Radarpistole aus dem Verkehr gezogen werden. Kenntnisse zur Funktionsweise dieser Geräte unterstützen dann die realistische Einschätzung solcher Messungen und mündige Aussagen dazu.
Die hier vorgeschlagene Struktur als Schulthema entspricht im Übrigen nicht der aktuellen physikalischen Argumentation. Seit die Geschwindigkeit des Lichts 1983 von der Conférence Générale des Poids et Mesures als Naturkonstante auf exakt 299 792 458 m/s festgelegt wurde, wird mit Hilfe dieser Naturkonstante die Länge eines Meters definiert (vgl. [3] Bureau International des Poids et Mesures, mehr Informationen zur Geschichte der Bestimmung der Lichtgeschwindigkeit im Artikel Drehspiegelexperiment). Für eine präzise Längenmessung sind Verfahren zur Bestimmung der Lichtgeschwindigkeit deshalb auch in der praktischen Physik bis heute relevant.
Eine Zugänglichkeit zum Thema wird gerade durch die Methode des Experiments ermöglicht, bei der man zwar nicht die Ausbreitung des Lichts, aber doch die Verzögerung des Signals, das sich eine gewisse Strecke bewegt hat, auf dem Osziloskop "mit eigenen Augen" sehen kann. Vorteilhaft an diesem speziellen Versuch ist der vergleichsweise einfach zu überblickende Aufbau. (Konkrete Vorteile zum Drehspiegelexperiment sind in Kuhn [4] (2006), S.77 dargelegt.)
Die Bestimmung der Lichtgeschwindigkeit ist abschließend vor allem auch auf Grund der Gegenwarts- und Zukunftsbedeutung ein Pflichtthema für allgemeinbildende Schulen. „Verfahren zur Bestimmung der Lichtgeschwindigkeit“ finden sich folglich auch im berliner Rahmenlehrplan (als Wahlthema 10 „Natur des Lichts“ in der Doppeljahrgangsstufe 9/10 [5] wieder.). Klafkis Kriterium der Zugänglichkeit ist insbesondere bei der Methode des Experiments gegeben, auf das nun genauer eingegangen werden wird.
Versuchsanleitung
Aufbau
Im Versuch wird der Gerätesatz Lichtgeschwindigkeitsmessung U8476460 der Firma MAPHY verwendet. Dieser besteht aus:
- Grundeinheit einschließlich Sender, Empfänger und eingebauter Netzversorgung
- Fresnellinse auf Stiel
- Triple-Prismen-Reflektor auf Stiel
- 3 BNC-Kabel
Zudem wird benötigt:
- Laser-Entfernungsmesser (oder ein vergleichbares Messgerät für Längen ≥1,5m)
- Oszilloskop mit Empfindlichkeit ≤100mV/DIV
- 2 Netzkabel (für Grundeinheit und Oszilloskop)
- 3 Stativfüße, -stangen und -klemmen
Auf Grund einer flexibleren Justierung, sollten alle 3 Bestandteile des Gerätesatzes (Grundeinheit, Linse, Reflektor) zuerst mit Stativstangen und -klemmen verlängert und in Stativfüßen befestigt werden. Mit den 3 BNC Kabeln ist die Grundeinheit mit dem Oszilloskop zu verbinden. Dabei ist 'B' das Referenzsignal (X oder Y1 am Oszilloskop), 'A' das Signal des am Reflektor zurückgeworfenen Strahls (Y ggf. 2 am Oszilloskop) und 'C' der Trigger. Grundeinheit, Linse und Reflektor sollten im Anschluss, wie Abb.2 zeigt, in einer optischen Achse ausgerichtet werden. (Eine schematische Darstellung des Aufbaues und der Kabelverbindungen findet sich in der Anleitung zum Gerätesatz von MAPHY.) Der minimale Abstand zwischen Grundeinheit und Reflektor beträgt 150 cm, wobei die Linse mittig anzuordnen ist. Das Oszilloskop ist nach dem Einschalten auf Zweikanalbetrieb mit einer Empfindlichkeit von ≤100mV/DIV auf beiden Kanälen, einer möglichst geringen Ablenkung (z.B. 10ns/DIV) und externer Triggerung (von Ausgang C der Grundeinheit) einzustellen.
Der Aufbau kann bis zu einer Entfernung von 8m zwischen Grundeinheit und Reflektor verwendet werden. Die korrekte Position der Linse kann mit folgender Gleichung berechnet werden, wenn a der Abstand Grundeinheit-Linse, b Linse-Reflektor und f=375mm die Brennweite der Fresnel-Linse ist:
Der richtige Abstand zwischen Linse und Grundeinheit lässt sich auch in kurzer Zeit durch probieren finden, indem der Peak des reflektierten Signals (Y ggf. 2 am Oszilloskop) maximiert wird. Ist auf diesem Kanal nur rauschen zu sehen (wie in Abb.3), so muss die Anordnung erneut ausgerichtet werden. Aus der in Abb.2 dargestellten Position ist - wie auch in dieser Abbildung zu sehen - ein roter Punkt sowohl auf der Fresnellinse (ca. 3mm), als auch auf dem Reflektor (ca. 3cm) deutlich zu sehen. Ähnelt die Anzeige des Oszilloskops dennoch nicht der in Abb. 2 dargestellten, so sollten die Einstellungen des Oszilloskops angepasst werden.
Durchführung
Nachdem der Aufbau abgeschlossen ist, kann die erste Messung beginnen. Um präzise Resultate zu erhalten, sollte die horizontale und vertikale Ausrichtung von Grundgerät und Linse vor jeder Messung erneut überprüft werden. Dann kann die Entfernung zwischen dem Strahlteiler, dessen Position auf dem Gehäuse der Grundeinheit eingezeichnet ist, und dem Reflektor z.B. mit einem Laserentfernungsmesser bestimmt werden. (Siehe Abb.3. Wir nennen diese Länge später a+b, um mit der oben eingeführten Nomenklatur konsistent zu bleiben. Multipliziert man diese Strecke mit zwei erhält man später die Strecke, die das Probesignal, im Vergleich zum Refernezsignal mehr zurücklegt.)
Wenn man die Maxima der beiden Signale auf dem Oszilloskop mit "Y-POS" auf eine Höhe bringt, so lässt sich die Zeitdifferenz zwischen der Detektion beider Signale ablesen. Dabei ist es zweckmäßig den horizontalen Abstand der Maxima abzulesen, sobald sich diese auf gleicher Höhe befinden. Diese Zeitdifferenz nennen wir - wie allgemein üblich - .
Nach einer Messung muss der Abstand Grundgerät-Reflektor nun mehrmals verändert werden. Dann muss insbesondere die Linse neu ausgerichtet werden. Je größer die Entfernung des Reflektors wird, desto näher (minimal 37cm) muss die Fresnellinse an der Grundeinheit positioniert werden. Wenn die Spitze des Probesignals wieder maximal ist, muss sie erneut auf die gleiche Höhe, wie das Referenzsignals skaliert werden. Dann kann die Zeitdifferenz zu dieser neuen - ebenfalls wie oben zu erfassenden - Länge a+b abgelesen werden.
Ergebnisse
Im Demopraktikum wurden - wie oben beschrieben - 8 Messwertpaare (Strecke a+b, Zeitdifferenz ) aufgenommen:
| (a+b) / m | 1,518 | 1,520 | 1,750 | 1,950 | 2,290 | 2,320 | 2,410 | 2,530 |
| / ns | 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Auswertung
Berücksichtigt man, dass die vom Probestrahl zusätzlich zurückgelegte Strecke das doppelte der Entfernung a+b ist, so kann man mit der Gleichung
folgende Geschwindigkeiten für den Probelichtstrahl berechnen.
| (a+b) / m | 1,518 | 1,520 | 1,750 | 1,950 | 2,290 | 2,320 | 2,410 | 2,530 |
| / ns | 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| / | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| / | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Die Ungenauigkeit des Ergebnisses setzt sich dabei aus den Fehlern der Länge (Positionierung des Entfernungsmessers an der Grundeinheit) und Zeitdifferenz (Ablesen am Oszilloskop) zusammen. Die Ableseungenauigkeit am Oszilloskop ist begründet in der Breite der Peaks, die die optische Bestimmung deren Abstands erschwert. Größtfehler bei der Längenmessung werden abgeschätzt, da sich keine größeren Abweichungen, bei der Messung zu verschiedenen Punkten auf dem Reflektor gezeigt haben. Die Präzision der beiden Geräte Oszilloskop und Laser-Entfernungsmesser ist deutlich höher. Der Gesamtfehler folgt aus der linearen Fehlerfortpflanzung:
Das Gesamtergebnis lautet somit:
.
Der oben angeführte Literaturwert liegt zwar in diesem Fehlerintervall, jedoch genau am unteren Rand. Das lässt gerade wegen der geringen statistischen Abweichung auf einen systematischen Fehler schließen: Entweder die Abstände wurden zu groß oder die Zeitunterschiede zu klein in die Endgleichung eingesetzt. Da die Bauweise für beide Detektoren in der Grundeinheit vermutlich gleich ist und auch die gleichen Kabel zum Oszilloskop verwendet wurden, ist eine systematische Abweichung in der Zeit unwahrscheinlich. Möglicherweise befindet sich die Kennzeichnung des Strahlteilers auf der Grundeinheit nicht exakt auf dessen Position. Möglicherweise wurde sogar eine Schaltung verbaut, die simuliert, dass der Strahlteiler genau an der Vorderkante der Grundeinheit sitzt. Das würde eine systematische Abweichung erklären. Genauen Aufschluss kann nur der genaue Aufbau der Grundeinheit geben und gerade da liegt der Haken dieses Experiments. Das eigentlich spannende Bauteil an diesem Versuch ist für Lehrer*innen und Schüler*innen - bis auf die Skizze am Gehäuse - nicht einsehbar. Wer wirklich die Endlichkeit der Lichtgeschwindigkeit hinterfragt, muss wohl den experimentellen und gedanklichen Aufwand der Drehspiegelmethode betreiben. Dieser Versuch ist der unpräziseste zur Bestimmung der Lichtgeschwindigkeit in diesem Wiki, jedoch ist er auch am einfachsten aufzubauen und deshalb durchaus als Schüler*innenexperiment geeignet.
Post Scriptum
Genau wie bei der Bestimmung der "Lichtgeschwindigkeit mit Hilfe von Lissajous-Figuren" wird im Grunde nur die Gruppengeschwindigkeit ermittelt, da nur ein endlicher (sich wiederholender) Wellenabschnitt betrachtet wird. In dispersionsfreien Medien ist die Phasengeschwindigkeit jedoch gleich der Gruppengeschwindigkeit. (vgl. Kuhn [4] (2006), S. 77)
Literatur
- ↑ 1,0 1,1 Klafki, W.: "Didaktische Analyse als Kern der Unterrichtsvorbereitung"; in: Roth, H.; Blumenthal, A.: "Reihe A AUSWAHL Grundlegende Aufsätze aus der Zeitschrift Die deutsche Schule - Didaktische Analyse", 11. Auflage, Hermann Schroedel Verlag KG, Hannover (1964), 1974, S. 15-22 Referenzfehler: Ungültiges
<ref>-Tag. Der Name „klafki“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Priemer, B.: "VORLESUNG: EINFÜHRUNG IN DIE DIDAKTIK DER PHYSIK" an: Humboldt-Universität zu Berlin (15.11.2013)
- ↑ Bureau International des Poids et Mesures: Resolution 1 of the 17th CGPM (1983); http://www.bipm.org/en/CGPM/db/17/1/ [21.08.2016]
- ↑ 4,0 4,1 Kuhn, W. (2006): Handbuch der experimentellen Physik Band 4/I: Optik, Aulis Verlag Deubner & Co. KG, Köln Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Feynman2“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Rahmenlehrplan Physik für die Sekundarstufe I, 1. Auflage (2006), Senatsverwaltung für Bildung, Jugend und Sport, Berlin
Siehe auch
Bestimmung der Lichtgeschwindigkeit mit Hilfe von Lissajous-Figuren
Mikrowellen: Bestimmung der Lichtgeschwindigkeit mit einem Mikrowellenherd