Balmer-Serie des Wasserstoffs
| Balmer-Serie des Wasserstoffs | |
 Beobachtung der Spektrallinien des atomaren Wasserstoffs | |
| Kurzbeschreibung | |
|---|---|
| Das Experiment dient der Bestimmung der Wellenlängen bzw. Frequenzen aus der Balmer-Serie des Wasserstoffs, mithilfe derer die Balmer-Formel durch Bestimmung der Rydbergfrequenz bzw. Rydbergkonstante überprüft werden kann. | |
| Kategorien | |
| Atom- und Kernphysik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Lisa Laudan |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Dr. Franz Boczianowski |
Das Emissionsspektrum des atomaren Wasserstoffs hat im sichtbaren Bereich drei Linien . 1885 fand Johann Jakob Balmer empirisch eine Formel für die Frequenzen der Serie (vgl. Demtröder [1] (2005), S. 102)
mit der Rydbergfrequenz [2]
- ,
wobei [3] als Rydbergkonstante bezeichnet wird.
Niels Bohr konnte diese Formel später mit seinem Atommodell erklären. Die Linien beruhen auf einen Übergang von Elektronen auf ein anderes Energieniveau. Die rote Linie entsteht beim Übergang von der dritten zur zweiten Schale, die türkise Linie beim Übergang von der vierten zur zweiten Schale und die blaue Linie beim Übergang von der fünften zur zweiten Schale. Die Balmer-Serie weist weitere Übergänge auf, deren Linien aber nicht sichtbar sind.
Inhaltsverzeichnis
Didaktischer Teil
Die quantenmechanische Berechnung der Energieniveaus des Wasserstoff-Atoms ist aufgrund ihrer Komplexität und Unverständlichkeit für die Schule ungeeignet, weshalb man auf vereinfachte Modelle und Näherungen zurückgreifen muss (siehe [4] milq). Betrachtet man verschiedene Schulbücher, wie Physik Oberstufe (2009) [2], Fokus Physik (2014) [3] oder Metzler Physik (2015) [4], so erfolgt der Zugang zum Wasserstoff-Atom häufig mithilfe des Bohrschen Atommodells. Dieses Modell weist sowohl Vorzüge als auch Grenzen auf.
Das Bohrsche Atommodell liefert gute Ergebnisse für das Spektrum des Wasserstoff-Atoms. Es ist für Schülerinnen und Schüler zudem leicht nachvollziehbar und vorstellbar. Zieht man den historischen Kontext hinzu, wird offenkundig, dass Bohr mit diesem Modell zum ersten Mal die klassische Physik in Frage stellte. Das Problem des Bohrschen Modells besteht jedoch darin, dass es bereits bei Atomen mit mehr als einem Elektron in der Hülle versagt. Außerdem sind die Annahmen des Modells nicht "aus einer tieferen Theorie" abgeleitet worden (vgl. Müller [5] (2003), S. 64f.).
Es wurden verschiedene Unterrichtskonzepte zur Quantenphysik entwickelt, welche zusammenfassend in (siehe Burkard [6] (2009), S. 19ff. ) analysiert worden sind. Nachfolgend werden einige Konzepte genannt, welche sich gegen die Anwendung des Bohrschen Atommodells aussprechen.
- 1. Bremer Konzept (siehe Niedderer [7] (1992), S. 88)
- Beim Bremer Konzept steht das Atommodell nach Schrödinger im Fokus. Das Bohrsche Atommodell wird nur soweit berücksichtigt, wie es von Schülerinnen und Schülern selbst eingebracht wird.
- 2. Münchner Konzept (siehe Müller [5] (2003), S. 109ff.)
- Das Münchner Konzept versucht der Vorstellung vom Planetenmodell des Atoms entgegenzuwirken und legt Wert auf quantenmechanische Konzepte.
- 3. Berliner Konzept (siehe Fischler [8] (1992), S. 244)
- Beim Berliner Konzept hält man zwar am Bohrschen Atommodell fest, jedoch wird das Wasserstoffatom ohne Anwendung des Bohrschen Atommodells behandelt.
Lichtfeldt und Fischler führten im Rahmen des Berliner Unterrichtskonzepts eine Untersuchung zu SchülerInnenvorstellungen über Quantenphysik durch. An dieser Stelle soll nur den Fragen nach der Atomvorstellung nachgegangen werden. Dafür wurden die Schülerinnen und Schüler gebeten, ein Bild des Wasserstoffatoms zu zeichnen. Außerdem sollten sie die Frage beantworten, warum Atomkern und Elektronen nicht "zusammenkleben" (vgl. Müller [5] (2003), S. 27).
Bilder des Wassserstoffatoms vor dem Quantenphysik-Unterricht:
- 70% "Planetenmodell"
- 21,9% "Elektronenwolke"
- 6,9% "Hantel"
Bilder des Wasserstoffatoms nach dem Quantenphysik-Unterricht:
- 57,8% "Planetenmodell"
- 25,2% "Elektronenwolke"
- 3,9% "Hantel"
- 10,8% "kein Bild"
Die Schülerinnen und Schüler vertreten sowohl vor als auch nach dem Unterricht verstärkt die Ansicht des Bohrschen Atommodells, da sie größtenteils das Bild der laufenden Elektronen auf Bahnen um den Kern zeichneten. Andere Schülerinnen und Schüler zeichneten eine verschmierte Wolke um den Atomkern. Die letzte Gruppe zeichnete chemische Strukturformeln von Molekülen, weshalb dieser Gruppe der Begriff "Hantel" zugeordnet wurde. Interessant ist auch, dass es nach dem Unterricht noch eine vierte Gruppe von Schülerinnen und Schülern gab, welche gar kein Bild des Wasserstoffatoms zeichneten. (siehe Müller [5] (2003), S. 27 und S. 30)
Stabilität der Atome vor dem Quantenphysik-Unterricht:
- 62,5% "Kreis"
- 22,5% "Ladung"
- 7,9% "Schale"
Stabilität der Atome nach dem Quantenphysik-Unterricht:
- 60,8% "Kreisbahn"
- 10,8% "Ladung"
- 12,7% "Schale"
- 5,9% "Lokalisation",
Auf die Frage bezüglich der Stabilität der Atome dominiert ebenfalls die Vorstellung der Elektronen, welche sich auf festen Kreisbahnen um den Kern bewegen. Die Gruppe "Ladung" erklärt die Stabilität aufgrund einer Ladungsabstoßung. Die Vorstellung von einer festen Schale (Hülle), auf der die Elektronen sitzen oder sich bewegen, vertreten nach dem Unterricht weniger Schülerinnen und Schüler. Auffällig ist auch hier wieder das Hinzukommen einer neuen Gruppe nach dem Unterricht, welche sich auf Erklärungen der Heisenbergschen Unbestimmtheitsrelation stützt. (siehe Müller [5] (2003), S. 27 und S. 30)
Das Münchner Konzept leitet aufgrund dieser und weiterer Studien und Untersuchungen (vgl. Müller [5] (2003), S. 17ff.) die nachfolgenden SchülerInnenvorstellungen zum Thema Atom ab. "Das Planetenmodell des Atoms ist eine sehr dominante und stabile Fehlvorstellung aus dem Bereich der Atomphysik. Die Elektronen im Atom werden als lokalisierte Objekte angesehen, die auf wohldefinierten Bahnen um den Atomkern kreisen" (Müller [5] (2003), S. 111).
Bezüglich dieser Atomvorstellung setzt sich das Münchner Konzept zum Ziel, das Bohrsche Atommodell aufgrund der Vertrautheit und Bekanntheit durch die Schülerinnen und Schüler aufzugreifen, aber dennoch auf die Gründe einzugehen, warum es sich nicht mit der Quantenmechanik vereinbaren lässt (Müller [5] (2003), S. 111).
Das Münchner Konzept, welches aus einem qualitativen Basiskurs und einem quantitativen Aufbaukurs aufgebaut ist, wurde mit Fragebögen und Interviews zu SchülerInnenvorstellungen evaluiert. Die Schülerinnen und Schüler vertraten nach Durchführung des Konzepts eine quantenmechanische Atomvorstellung und lehnten das Bohrsche Atommodell überwiegend ab. Viele Schülerinnen und Schüler benutzten das Bohrsche Atommodell als Ausgangspunkt und sprachen sich gegen dieses aus. "Diese Ergebnisse können als eine Bestätigung des Ansatzes aufgefasst werden, das Bohrsche Atommodell im Unterricht nicht zu vermeiden, sondern auf dem Hintergrund der Ergebnisse aus dem Basiskurs (Doppelspaltexperiment/Ortseigenschaft, Unbestimmtheitsrelation) im Detail darauf einzugehen, warum das Bohrsche Atommodell keine adäquate quantenmechanische Beschreibung von Atomen darstellt" (Müller [5] (2003), S. 164).
Das Bild der kreisenden Elektronen auf den Bahnen prägt sich oft bei den Schülerinnen und Schülern ein. Aus quantenmechanischer Sicht ist diese Betrachtung problematisch, da es zu Fehlvorstellungen seitens der Schülerinnen und Schüler führen kann (vgl. [5] milq). Das Münchner Internetprojekt zur Lehrerfortbildung in Quantenmechanik (kurz: milq) der Universität München hat grundsätzlich keine Einwände gegen die Berechnung des Grundzustandes des Wasserstoff-Atoms "durch Minimierung der Gesamtenergie in Abhängigkeit vom Atomradius" (Wiesner und Müller [9] (1996), S. 2). Für diese Herangehensweise sollte jedoch klar gemacht werden, dass es sich hierbei um eine Abschätzung und nicht um eine strenge Herleitung handelt (vgl. Wiesner und Müller [9] (1996), S. 2).
Das Projekt schlägt außerdem eine weitere Methode zur Berechnung vor, indem "das Coulomb-Potential des Kerns durch ein geeignet angepasstes Kastenpotential ersetzt" (siehe [6] milq) wird. Die ausführliche Berechnung kann man hier nachlesen.
Für detaillierte Informationen der einzelnen Konzepte sollte die jeweilige Literatur hinzugezogen werden. Herr Drobniewski hat sich ebenfalls in dem didaktischen Teil seines Wiki-Artikels mit diesen und weiteren Konzepten befasst (siehe [7]).
Versuchsanleitung
Dieser Versuch wurde mithilfe der Anleitung der Firma Leybold durchgeführt (siehe [8] Leybold).
Aufbau
Für die Durchführung des Experiments werden verschiedene Geräte benötigt:
- Balmer-Lampe (Leybold 451 13),
- Betriebsgerät zur Balmer-Lampe (Leybold 451 14),
- optische Bank (Länge 1 m),
- 5 Optikreiter für:
- Linse 1 (f = 50 mm),
- verstellbarer Spalt,
- Linse 2 (f =1 00 mm),
- Gitter (g = 600 mm-1) mit Halterung,
- Beobachtungsschirm (25 cm x 25 cm),
- Lineal.
Die optische Bank wird direkt vor die Balmer-Lampe gestellt. Die Halterungen der Linsen, des Spalts, des Gitters und des Schirms werden jeweils mit den Optikreitern befestigt. Nun werden diese in bestimmten Abständen auf die optische Bank gestellt.
| Reihenfolge | Linse 1 | Spalt | Linse 2 | Gitter | Schirm |
|---|---|---|---|---|---|
| Abstände [cm] | 8 | 16 | 31 | 38 | 62 |
Hinweis:
Die Abstände dienen vorerst nur der groben Orientierung, da der Versuch noch einer Feinjustierung bedarf. Daher ist es möglich, unterschiedliche Optikreiter zu verwenden. Lediglich die Optikreiter des Gitters und des Schirms sollten die gleiche Breite aufweisen, um den Abstand zwischen beiden Geräten exakt bestimmen zu können. Für die ersten drei Geräte wurden 3 Optikreiter der Breite 50 mm (Leybold 460 352) und für das Gitter und den Schirm zwei Optikreiter der Breite 34 mm (Leybold 460 353) verwendet, da zu dieser Zeit nicht fünf Optikreiter gleicher Breite vorhanden waren.
Durchführung
Das Betriebsgerät wird nun erstmals angeschlossen und eingeschaltet, so dass die Balmer-Lampe leuchtet. Ich verweise an dieser Stelle auf die Sicherheitshinweise. Für die Feinjustierung nimmt man den Optikreiter mit dem Gitter zunächst von der Bank. Nun verschiebt man die erste Linse (f = 50 mm) entlang der optischen Achse vor und zurück, bis das Licht der Balmer-Lampe scharf auf dem Spalt abgebildet wird. Anschließend stellt man durch Verschieben der zweiten Linse (f = 100 mm) das Bild auf dem Schirm scharf.
Nach der Feinjustierung kann das Gitter wieder eingesetzt werden und die Optikreiter können auf der optischen Bank befestigt werden. Der Raum muss nun vollständig abgedunkelt werden, um die drei Linien der Balmer-Serie auf dem Schirm zu beobachten. Mithilfe des verstellbaren Spalts können die Linien scharf gestellt werden.
Der nachstehenden Tabelle kann man die Werte für die Abstände nach der Feinjustierung entnehmen. Der Wert wurde dabei immer an der vorderen Kante des Optikreiters auf der optischen Bank abgelesen.
| Reihenfolge | Linse 1 | Spalt | Linse 2 | Gitter | Schirm |
|---|---|---|---|---|---|
| Abstände [cm] | 8,3 | 15,8 | 31,1 | 37,8 | 62,2 |
Wenn alle drei Linien scharf auf dem Schirm abgebildet sind, kann ihre Position und die der 0-ten Beugungsordnung auf dem Schirm markiert werden. Anschließend kann das Licht im Experimentierraum wieder angeschaltet und die Balmer-Lampe vorerst ausgeschaltet werden.
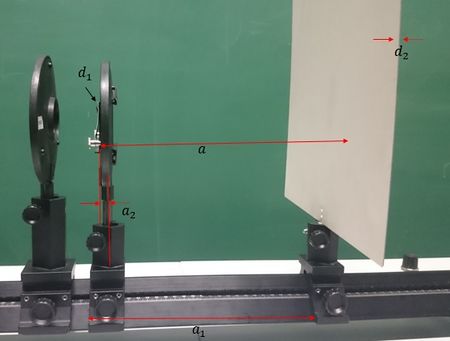
Bevor der Schirm abgenommen wird und die jeweiligen Abstände der Beugungsordnungen gemessen werden, muss zunächst der Abstand a zwischen Gitter und Schirm bestimmt werden. Dafür sind verschiedene weitere Abmessungen notwendig, denn für den Abstand a gilt . Dabei steht a1 für den Abstand zwischen den zwei Optikreitern, wobei jeweils an der vorderen Kante gemessen wird, weshalb es hier notwendig ist, dass beide Optikreiter dieselbe Breite aufweisen. Der Abstand a2 besteht zwischen Stielmitte und Halterrand des Gitters. d1 ist die Dicke des Gitters und d2 die Dicke des Schirms (siehe Abb. 4).
Nachdem die vier Parameter bestimmt wurden, kann nun der Schirm abgenommen und die Abstände der drei Linien zur 0-ten Beugungsordnung bestimmt werden.
Ergebnisse
| Optikreiter Gitter - Optikreiter Schirm | a1 = 244 mm |
|---|---|
| Stielmitte - Halterrand (Gitter) | a2 = 4 mm |
| Dicke des Gitters | d1 = 2 mm |
| Dicke des Schirms | d2 = 1 mm |
Gitterabstand:
| Farbe | Abstandlinks [mm] | Abstandrechts [mm] |
|---|---|---|
| rot | 103 | 112 |
| türkis | 74 | 79 |
| blau | 66 | 69 |
Auswertung
Formeln
Für die Wellenlängen der Linien gilt folgende Formel (vgl. Demtröder [10] (2009), S.330 f.)
- .
Der Abstand d ergibt sich aus der Gitterkonstanten (g = 600 mm-1) zu
- .
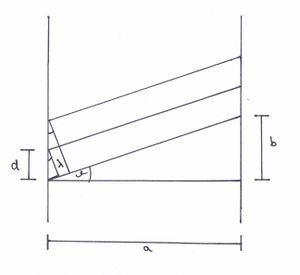
Aus Abbildung 6 ergibt sich der nachstehende Zusammenhang.
- a: Gitterabstand
- b: Linienabstand
Somit gilt für die Wellenlänge
- .
Für die Frequenz folgt mit
- .
- c: Vakuumlichtgeschwindigkeit
Messunsicherheiten
Für die Messunsicherheit der Längenmessung gilt
- .
Die systematische und zufällige Messabweichung wird jeweils mit abgeschätzt. Der systematische Fehler beträgt eine halbe Skaleneinheit des Lineals. Der zufällige Fehler entspricht dem Ablesefehler, welcher abgeschätzt wurde. Diese Messunsicherheit betrifft die Parameter a1, a2, d1, d2 und b.
Fehlerfortpflanzungen
Da es sich bei der Formel für den Gitterabstand a um eine additive Funktion handelt, ergibt sich deren Unsicherheit zu
- .
Bei der Formel zur Berechnung des Sinus des Winkels handelt es sich um eine multiplikative Funktion mit Potenzen. Für die Unsicherheit von folgt
mit
- .
Die Fehlerfortpflanzung für die Wellenlänge ergibt sich aus dem Fehler von zu
- .
Für die Frequenz folgt somit eine Unsicherheit von
- .
Die Grundlagen und Formeln zur Berechnung der Messabweichungen und Messunsicherheiten wurden aus den Unterlagen des Physikalischen Grundpraktikums entnommen (vgl. Müller [11] (2007), S. 11 ff.).
Berechnungen der Wellenlängen bzw. Frequenzen
Aus den besprochenen Formeln, deren Unsicherheiten und den gemessenen Größen ergeben sich folgende Werte für die Wellenlängen bzw. Frequenzen der einzelnen Linien. Die Berechnungen erfolgten mithilfe von Excel.
| Farbe | b [mm] | ub [mm] | sin ν | usin ν | λ [mm] | uλ [mm] | λ [nm] | uλ [nm] | ν [THz] | uν [THz] |
|---|---|---|---|---|---|---|---|---|---|---|
| rot | 107,5 | 0,707106781 | 0,395027751 | 0,002615362 | 0,00065838 | 4,35894E-06 | 658,3795844 | 4,358936727 | 455,3489584 | 3,014730932 |
| türkis | 76,5 | 0,707106781 | 0,292607213 | 0,002718256 | 0,000487679 | 4,53043E-06 | 487,6786883 | 4,530427032 | 614,7335637 | 5,710738692 |
| blau | 67,5 | 0,707106781 | 0,260665852 | 0,002743015 | 0,000434443 | 4,57169E-06 | 434,4430872 | 4,571691711 | 690,0615221 | 7,261592218 |
| Farbe | Linie | λ [nm] | ν [THz] | |
|---|---|---|---|---|
| rot (m = 3) | Hα | 658 | 455 | 0,1389 |
| türkis (m = 4) | Hβ | 488 | 615 | 0,1875 |
| blau (m = 5) | Hγ | 434 | 690 | 0,2100 |
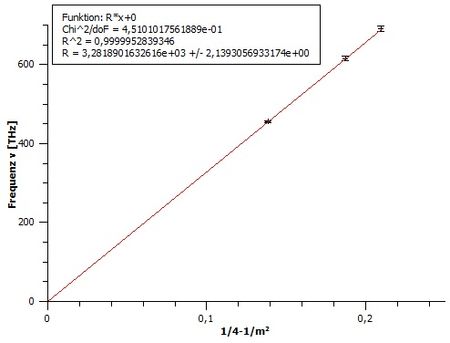
Um die Balmer-Formel
zu überprüfen, kann man die Frequenz in Abhängigkeit von plotten. Dafür kann man zum Beispiel das Programm qti-plot verwenden. Die Steigung der eingezeichneten Ursprungsgerade entspricht der Rydbergfrequenz . Dieser Wert liefert gute Übereinstimmung mit dem Referenzwert .
Hinweis: Da die Frequenz im Diagramm in THz angegeben ist, muss der Wert der Ursprungsgerade noch mit dem Faktor 1012 multipliziert werden, um die Rydbergkonstante in der Einheit Hz bzw. s-1 zu erhalten.
Sicherheitshinweise
Für den Einbau der Balmer-Lampe ist vorher die Gebrauchsanweisung zu lesen. Für die Balmer-Lampe von Leybold mit der Gerätenummer 451 13 findet man diese hier.
Das Betriebsgerät darf nur eingeschaltet sein, wenn die Balmer-Lampe eingebaut ist.
Die heiße Balmer-Lampe sollte nicht berührt werden.
Literatur
- ↑ Demtröder, W. (2005): Experimentalphysik 3 - Atome, Moleküle und Festkörper; Springer-Verlag Berlin Heidelberg
- ↑ Diehl et al. (2009): Physik Oberstufe Gesamtband; Cornelsen; Berlin; S. 333f.
- ↑ Ackermann et al. (2014): Fokus Physik Gesamtband SII; Cornelsen; Berlin; S. 336f.
- ↑ Grehn und Krause (Hrsg.) (2015): Metzler Physik; Schroedel; Braunschweig, S. 414f.
- ↑ 5,0 5,1 5,2 5,3 5,4 5,5 5,6 5,7 5,8 Müller, Rainer (2003): Quantenphysik in der Schule; Logos Verlag Berlin Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. Referenzfehler: Ungültiges<ref>-Tag. Der Name „Müller“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Burkard, Ulrike (2009):Quantenphysik in der Schule - Bestandsaufnahme, Perspektiven und Weiterentwicklungsmöglichkeiten durch die Implementation eines Medienservers; Logos Verlag Berlin
- ↑ Niedderer, Hans (1992): Atomphysik mit anschaulichem Atommodell. In: Fischler, Helmut (Hrsg.) (1992): Quantenphysik in der Schule; IPN Kiel
- ↑ Fischler, Helmut (1992): Die Berliner Konzeption einer "Einführung in die Quantenphysik" - Didaktische Grundsätze und inhaltliche Details. In: Fischler, Helmut (Hrsg.) (1992): Quantenphysik in der Schule; IPN Kiel
- ↑ 9,0 9,1 Wiesner, Hartmut und Müller, Rainer (1996): Stabilität und Spektrum der Atome; Physik in der Schule 34, 48, verfügbar unter [1] [01.07.2016] Referenzfehler: Ungültiges
<ref>-Tag. Der Name „MüllerWiesner“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Demtröder, W. (2009): Experimentalphysik 2 - Elektrizität und Optik; Springer-Verlag Berlin Heidelberg
- ↑ Müller, U. (2007): Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik; Humboldt-Universität zu Berlin, verfügbar unter PGP HU-Berlin [02.06.2016]
Siehe auch
- Wiesner, Müller: Stabilität und Spektrum der Atome; http://homepages.physik.uni-muenchen.de/~milq/kap13/images/quant2.pdf [01.07.2016]
- CODATA: Rydbergfrequenz; http://physics.nist.gov/cgi-bin/cuu/Value?rydchz [06.06.2016]
- CODATA: Rydbergkonstante; http://physics.nist.gov/cgi-bin/cuu/Value?ryd [06.06.2016]
- LEYBOLD: Balmer-Serie des Wasserstoffs; http://www.ld-didactic.de/documents/de-DE/EXP/P/P6/P6211_d.pdf [02.06.2016]
- milq: Energiewerte des Wasserstoff-Atoms durch Kastenpotential-Näherung; http://homepages.physik.uni-muenchen.de/~milq/kap13/k131p01.html [01.07.2016]
- milq: Kapitel 13: Das Wasserstoff-Atom; http://www.milq-physik.de/13._Wasserstoff-Atom [01.07.2016]
- Wiki-Artikel Kai Drobniewski: Absorption der Natrium-Spektrallinie; https://www.physikalische-schulexperimente.de/physo/Absorption_der_Natrium-Spektrallinie [01.07.2016]