Über einen den Photoeffekt betreffenden didaktischen Gesichtspunkt
| Über einen den Photoeffekt betreffenden didaktischen Gesichtspunkt | |
 Aufbau zum Photoeffekt mittels der Gegenfeldmethode | |
| Kurzbeschreibung | |
|---|---|
| Quantitative Bestimmung der Einsteingeraden und des Planck'schen Wirkungsquantums | |
| Kategorien | |
| Atom- und Kernphysik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung, Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | schwer |
| Informationen | |
| Name: | Kristoph Schumann |
| Kontakt: | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{schumann}} @Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \text{physik.hu-berlin.de}} |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Der Photoeffekt zählt zu den wegweisenden Experimenten hin zu einer quantenphysikalischen Beschreibung des Lichts.
Die in diesem Zusammenhang erstmal 1888 von Heinrich Hertz beobachteten und von seinem Assistenten Wilhelm Hallwachs systematisch untersuchten Phänomene (Hallwachs, 1888a[1] und 1888b[2]) standen im Widerspruch zur etablierten Beschreibung des Lichts als Welle. Erst Albert Einstein konnte 1905 eine schlüssige Erklärung liefern, indem er Lichtquanten (Photonen) mit frequenzabhängiger Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=h \cdot f} (mit Plank'schem Wirkungsquantum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} ) postulierte – analog zu der erst wenige Jahre zuvor von Max Planck beschriebenen Quantelung der Strahlungsenergie. Für diese unter dem Titel Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt[3] veröffentlichten Arbeit erhielt er später den Nobelpreis.
Ziel des hier beschriebenen Versuchs ist die Aufnahme von Kennlinien einer Photozelle bei Beleuchtung mit verschiedenen Spektrallinien einer Hg-Lampe. Aus den mit dieser Gegenfeldmethode ermittelten Energien der ausgelösten Elektronen kann anhand der Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=h f - W_A} (mit Austrittsarbeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_A} ) das Plank'sche Wirkungsquantum bestimmt werden.
Inhaltsverzeichnis
Didaktischer Teil
In diesem Abschnitt soll erläutert werden, welchen Beitrag ein Experiment über den Photoeffekt zu einer historischen Kontextualisierung vor dem Hintergrund eines authentischen Experimentierbegriffs für den Physikunterricht leisten kann. Dazu wird zuerst anhand von Höttecke & Rieß (2015[4]) der Begriff des authentischen Experimentierens erläutert, dann auf die Rolle einer historischen Kontextualisierung im authentischen Experimentieren eingegangen und abschließend das Experiment zum Photoeffekt prinzipiell darin verortet.
Authentisches Experimentieren
Für Höttecke & Rieß (2015[4]) ist Authentizität eine zentrale Eigenschaft naturwissenschaftlichen Experimentierens im Unterricht. Sie schreiben dem Begriff eine Funktion als Brücke über die „Kluft zwischen Wissenschaftskultur, -praxis, Laboren, Experimenten und Forschen auf der einen Seite und Schule, Unterricht, Lehrkraft, Schüler und Lernen auf der anderen“ (Höttecke & Rieß 2015[4], S. 128) zu. In Anlehnung an Buxton (2006[5]) beschreiben sie drei Dimensionen des Begriffes, nämlich youth-centered, contextual und canonical, was sie mit Orientierung des Authentizitätsbegriffs am Kind/Schüler, Kontext als curricularer Referenzpunkt und Forschungspraxis in den Naturwissenschaften übersetzen. Dabei stellen sie fest, dass die ersten beiden Dimensionen generell recht anerkannt und in Umsetzung begriffen sind, zwischen den Experimentalpraktiken der Forschung und dem Experimentier-Lernhandeln von Schülern/innen allerdings tiefgreifende Unterschiede bestehen (Höttecke & Rieß 2015[4], S. 128 f.).
Historische Kontextualisierung
Eine Möglichkeit zur Überbrückung dieser Kluft besteht für Höttecke & Rieß (2015[4]) in der historischen Kontextualisierung. Der wissenschaftshistorische Aspekt wird in dem Artikel anhand einiger Beispiele, meist aus dem Bereich der Elektrizitätslehre und des Magnetismus betrachtet (Höttecke & Rieß 2015[4], S. 131, 134, 135). Dabei stellen die Autoren fest, dass Lehrbücher häufig eine systematische Rekonstruktionslogik statt einer historischen verfolgen, wodurch ein induktivistisches Forschungsparadigma (erst Messen, dann Theorie entwickeln) bei den Lernenden erzeugt wird, das einer Authentizität abträglich ist. Im Gegensatz dazu betonen sie die Wichtigkeit des Ermöglichen des Neuen beim Experimentieren, die Rolle von Improvisation und Zufall und das Eigenleben des Experiments, wodurch Theoriebildung nicht im Nachhinein, sondern verschränkt mit den experimentellen Tätigkeiten erfolgt (Höttecke und Rieß 2015[4], S. 131–133).
Neben dem in diesem Artikel betrachtetem Photoeffekt bietet sich zum Beispiel auch eine historische Kontextualisierung in der Behandlung der Wärmekraftmaschinen an, wie in dem umfangreichen Wiki-Artikel zur historischen Entwicklung der Wärmekraftmaschinen beschrieben.
Einordnung des Experiments zum Photoeffekt
Die Quantenphysik – soweit sie in ihren Anfängen in der Schule behandelt wird – kann eine hervorragende Gelegenheit zu einer historischen Kontextualisierung bieten. In ihrem Fall stimmt nämlich der historische Gang meist mit der systematischen Rekonstruktionslogik überein, da im Unterricht und in Lehrbüchern (vgl. dazu z.B. Metzler Physik[6], S. 380) oft direkt zuvor der Wellen- aber noch nicht der Teilchencharakter des Lichtes thematisiert wurde. Somit herrscht eine ähnliche Ausgangslage bei der Behandlung des Photoeffekts im Unterricht, wie bei seiner Entdeckung im ausgehenden 19. Jahrhundert. Eine historische Kontextualisierung kann nun vorgenommen werden, indem (nach einer ggf. nötigen Wiederholung der Experimente zur Brechung, Beugung und Interferenz von Licht) zuerst Hallwachs Experimente mit der Zinkplatte (siehe dazu als historische Dokumente Hallwachs 1888a[1] und Hallwachs 1888b[2]) gezeigt und die Widersprüche der Beobachtungen zu der Theorie diskutiert werden, damit dann die Erklärung im Rahmen des Photonenbild nach Einstein (1905[3]) als eine schlüssigere Theorie eingeführt werden kann. Dabei sollte durchaus auf die vielen Kontroversen eingegangen werden, die es in dieser Zeit gab, und die Leistung Einsteins, für die er ja den Nobelpreis erhielt, entsprechend gewürdigt werden.
In Zusammenfassung dieser Ausführungen kann die historische Kontextualisierung der Dimension der Forschungspraxis in den Naturwissenschaften zugeordnet werden, wobei die Verschränkung von experimentellen Tätigkeiten mit Theoriebildung einen zentralen Beitrag zur Authentizität des Experimentierens darstellt. Der Photoeffekt als ein entscheidendes Experiment zur Lösung der Widersprüche eines alleinigen Wellenbilds des Lichts bietet dafür einen guten Anlass.
Versuchsanleitung

Für eine Einbettung des hier beschriebenen Versuchs in eine historische Unterrichtsreihe bietet es sich an, zuvor schon anhand der auf Hallwachs zurückgehenden Experimente die Lichtquantenhypothese einzuführen. Eine Beschreibung dieses qualitativen Nachweis des Herauslösens von Elektronen aus Metalloberflächen über das Elektroskop kann in dem Artikel Der Photoeffekt (im Entstehen) gefunden werden. Der folgende Versuch kann anschließend damit motiviert werden, den Wert des in der Gleichung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=h \cdot f - W_A} schon genannten Plank'schen Wirkumsquantums selbst näherungsweise zu bestimmen.
Aufbau
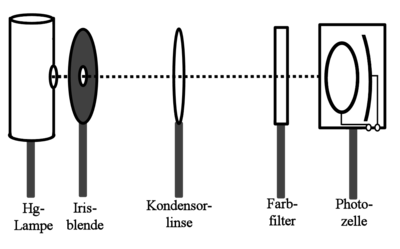
Der Versuch zum Photoeffekt gliedert sich in einen optischen Aufbau und eine Schaltung von Messgeräten zur Aufnahme der Kennlinien nach der Gegenfeldmethode. Beide sind schematisch in Abb. 1 und 2 dargestellt. Ein Foto des gesamten Aufbaus findet sich auch in der Kurzbeschreibung im Kasten oben links auf dieser Seite.
Der optische Aufbau folgt weitgehend der Beschreibung des Versuchs P6.1.4.3 von Leybold (siehe [1]). Als Geräte wurden hier verwendet:
- Photozelle mit Ringanode (Leybold, Seriennr. 558 77) im Gehäuse
- Quecksilber-Hochdrucklampe (Leybold, Seriennr. 451 062) im Gehäuse (Leybold, Seriennr. 451 16)
- Universaldrossel für die Lampe (Leybold, Seriennr. 451 30)
- Interferenzfilter (Wellenlängen 405 nm, 436 nm, 546 nm und 580 nm)
- Irisblende, Linse (Brennweite: +100 mm) und Halter für Interferenzfilter
- optische Bank mit 5 optischen Reiter
Der in Abb. 2 dargestellte elektrische Aufbau orientiert sich dagegen nicht an der Beschreibung von Leybold sondern eher an den Ausführungen in Meyn (2015[7], S. 112 ff.). Dazu wurden verwendet:
- Labornetzgerät DIGI40 (Voltcraft)
- Messverstärker (Neva)
- Digital Multimeter (Frederiksen, Seriennr. 3867.70 und PeakTech, Seriennr. 2010 DMM)
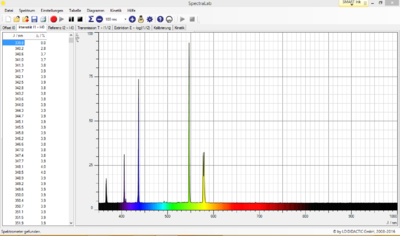
Die verwendete Spektrallampe hat dabei ein deutlich ausgeprägtes Linienspektrum, wie durch eine Messung mit SpectraLab (siehe Abb. 3) bestätigt werden konnte. Das Spektrum konnte durch die Interferenzfilter auf einzelne Linien eingeschränkt werden, die hier alle dem sichtbaren Bereich von etwa 400 bis 600 nm entnommen wurden. Mit Hilfe der Linse wurde das Licht der Spektrallampe auf die Kathode der Photozelle fokussiert. Die Filter wurden dabei direkt vor das Gehäuse der Photozelle gestellt. So konnte der Einfluss von Streulicht wirkungsvoll unterbunden werden. Nichtsdestotrotz wurden alle Versuche in einem abgedunkelten Raum durchgeführt.
Durchführung
Hg-Lampe und Wahl der Spektrallinie
Um das Plank’sche Wirkungsquantum zu bestimmen, müssen die Kennlinien für verschiedene Frequenzen des einfallenden Lichts bestimmt werden. Dazu braucht nur der Interferenzfilter gewechselt werden. Für jede Frequenz erfolgt dann die Bestimmung der kinetischen Energie der schnellsten Elektronen auf die gleiche Art und Weise nach der Gegenfeldmethode.
Zu Beginn der Messungen sollte als erstes die Quecksilber-Hochdrucklampe in Betrieb genommen werden, da diese eine Aufwärmzeit (etwa 10 Minuten) benötigt. Wurde der Aufbau wie oben beschrieben vorgenommen, sollte das Licht durch die Linse auf die Rückseite der Photozelle fokussiert werden. Wie das überprüft und ggf. nachjustiert werden kann, wird in der Anleitung von Leybold beschrieben und kann dort nachgelesen werden.
Messverstärker und Photostrom
Wird die Photozelle wie beschrieben mit dem Licht einer bestimmten Wellenlänge bestrahlt, führt der Phototeffekt zu einer Übertragung von Energie auf freie Elektronen im Kathodenmaterial. Diese werden ausgelöst und können dann aufgrund der verbliebenen kinetischen Energie den Raum innerhalb der Photozelle durchqueren und zur Anode gelangen. Der so entstehende Photostrom liegt in der Größenordnung von Nano- bis Pikoampere (wobei ein Pikoampere immer noch beachtlichen 6 Millionen Elektronen pro Sekunde entspricht, wie eine kurze Abschätzung zeigt). Um diesen Strom zu messen, wird also ein Messverstärker benötigt. Zeigt das an den Messverstärker angeschlossene Multimeter dabei auch bei hohen Verstärkung keinen Ausschlag, kann das verschiedene Gründe haben. Zunächst sollte zu Beginn ein Interferenzfilter mit möglichst niedriger Wellenlänge gewählt werden, da dort im Allgemeinen ein höherer Photostrom erreicht werden kann. Auch kann es sein, dass die Photozelle falsch herum angeschlossen wurde (und der sich ergebende Strom negativ ist). Das kann über einen Umpolungsschalter am Multimeter überprüft werden. Anschließend sollten nacheinander die verwendete Photozelle, das Multimeter und so möglich auch der Messverstärker getauscht werden, um Fehlfunktionen der Geräte auszuschließen. Wenn ein Photostrom angezeigt wird, kann mit der Aufnahme der Kennlinien begonnen werden.
Netzgerät und Gegenfeldmethode
Das Prinzip der Gegenfeldmethode beruht darauf, den aus der Kathode der Photozelle ausgelösten Elektronen ein zu überwindenden elektronisches Feld zwischen Anode und Kathode entgegenzustellen, das die Elektronen abbremst, zum Stillstand bringt und dann auf die Kathode zu beschleunigt. Dieses Feld wird durch eine am Netzgerät eingestellte Gegenspannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_G} erzeugt. Da der fließende Photostrom ein Maß für die Anzahl der Elektronen ist, die die Anode erreichen, ist der Wert der Spannung von Bedeutung, bei der dieser gerade Null wird, also der Nulldurchgang der Kennlinie. An diesem Punkt erreichen die schnellsten Elektronen, deren kinetische Energie der Energie der Photonen abzüglich der Austrittsarbeit entspricht, gerade die Anode nicht mehr. Diese Spannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{G,0}} gibt somit nach der Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=qU} die Energie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E } in der Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=h f - W_A} in Elektronenvolt (eV) an.
Ein möglicher Fehler kann hierbei entstehen, wenn das Netzteil falsch herum angeschlossen ist, die Elektronen also nicht abbremst, sondern beschleunigt. Falls der Photostrom mit Erhöhung der Spannung nicht sinkt, sollte also der Netzgerät umgepolt werden.
Aufnahme einer Kennlinie
Um eine Kennlinie aufzunehmen, wird die Spannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_G} am Netzgerät schrittweise erhöht und der sich ergebende Photostrom Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): I gemessen. Wenn dieser an der unteren Grenze des jeweiligen Messbereichs anlangt, sollte zuerst der Bereich am Multimeter angepasst werden. Bleibt der angezeigte Wert dennoch bei Erhöhung der Spannung etwa gleich, kann am Messverstärker eine höhere Verstärkung eingestellt werden, da zu kleine Werte am Multimeter teilweise nicht korrekt ausgegeben werden. Bleibt die Stromstärke auch bei höheren Spannungen (über zwei Volt) deutlich über Null, liegt wahrscheinlich ein Defekt vor. In diesem Fall sollte auch wieder erst die Photozelle, dann das Multimeter und der Messverstärker getauscht werden. Für die spätere Auswertung ist es darüber hinaus ratsam, in der Nähe des Nulldurchganges mehr Messwerte aufzunehmen, also kleinere Intervalle bei der Spannung zu wählen.
Oft wird nach dem Nulldurchgang ein negativer Photostrom gemessen, wenn die Spannung weiter erhöht wird. Als mögliche Ursache dafür nennen Bormann & Kuhn (1996[8], S. 98 f.) aus der Anode ausgelöste Elektronen, die durch die angelegte Spannung beschleunigt statt abgebremst werden.
Einsteingerade
Aus den aufgenommenen Kennlinien kann dann in einem geeigneten Programm (qti-Plot, origin oder ähnliche) durch eine Regressionsrechnung die Spannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{G,0}} im Nulldurchgang bestimmt werden. Die so für verschiedene Wellenlängen ermittelten maximalen kinetischen Energien der Elektronen ergeben, aufgetragen als Funktion der Frequenz des Lichtes, einen linearen Verlauf, die sogenannte Einsteingerade. Gemäß der Formel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=h f - W_A} kann daraus durch lineare Regression das Plank’sche Wirkumsquantums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} bestimmt werden.
Ergebnisse
Für die hier beschriebenen Messungen wurden vier Spektrallinien mit Wellenlängen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{1}=405\pm10~\mathrm{nm}, \lambda_{2}=436\pm10~\mathrm{nm}, \lambda_{3}=546\pm10~\mathrm{nm}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{4}=580\pm10~\mathrm{nm}} benutzt. Die Angabe der Wellenlänge wurde dabei von den verwendeten Interferenzfiltern übernommen, die Unsicherheit entspricht der Halbwertsbreite, die aus der in Abb. 3 dargestellten Spektralmessung abgeschätzt wurde.
Für diese Spektrallinien wurden nacheinander Kennlinien aufgenommen. Dabei wurde am Messverstärker für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{2}} eine Verstärkung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1~\mathrm{V}=1~\mathrm{nA}} benutzt, für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{3}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{4}} dagegen eine Verstärkung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1~\mathrm{V}=100~\mathrm{pA}} . Darüber hinaus wurden um den Nulldurchgang herum auch für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{2}} weitere Messungen mit einer Verstärkung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1~\mathrm{V}=100~\mathrm{pA}} durchgeführt, um diesen präziser bestimmen zu können. Die Unsicherheit der Spannungsmessung wurde dabei mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,01~\mathrm{V}+1\%} abgeschätzt, die Unsicherheit der Stromstärkenmessung je nach eingestellter Verstärkung mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,05} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,005~\mathrm{nA}+5\%} . Durch den im Vergleich zur Spannungsmessung höheren prozentualen Fehler wird dabei versucht, den Einfluss des Messverstärkers zu berücksichtigen. Die Anpassung des absoluten Wertes bildet in beiden Fällen den Ablesefehler ab.
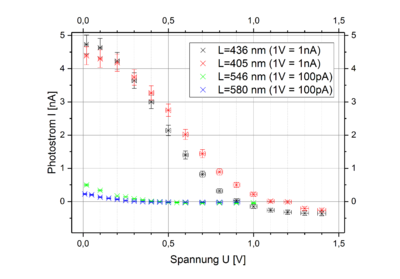
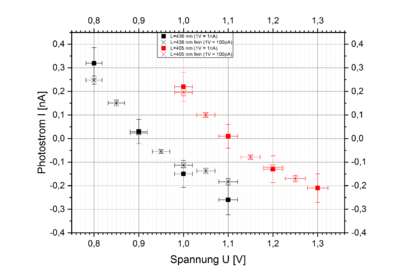
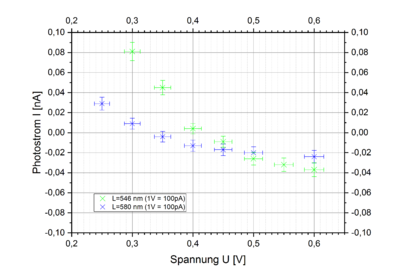
In Abb. 4 sind die Verläufe aller vier Kennlinien im Groben dargestellt. Abb. 5 erlaubt einen Vergleich der Werte für beide Verstärkungen bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{2}} . Dabei ergibt sich als genereller Verlauf (s. z.B. die schwarzen Punkte in Abb. 4) eine Abnahme der Stromstärke mit steigender Spannung, wobei am Rand zum Teil ein Abflachen beobachtet werden kann. Wurde die Spannung über 1,5 V erhöht, blieben die gemessenen Stromstärken bis mindestens 5 V konstant (nicht in der Abb. dargestellt). Es fällt auf, dass für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{3}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{4}} deutlich geringere Stromstärken beobachtet wurden, wenngleich auch hier ein Abfall der Werte auftrat. Abb. 6 zeigt die Nulldurchgänge für diese beiden Wellenlängen in einer ähnlichen Auflösung wie Abb 5. Im Vergleich der vier Kennlinien ist festzustellen, dass der Nulldurchgang für größere Wellenlängen bei kleineren Gegenspannungen erreicht wurde.
Vergleicht man in Abb. 5 die Werte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{2}} für beide Verstärkungen, kann von einer recht guten Übereinstimmung im Rahmen der Messunsicherheit gesprochen werden. Lediglich im Bereich negativen Photostroms flachen für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{2}} die Werte bei der höheren Verstärkung (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1~\mathrm{V}=100~\mathrm{pA}} ) stärker ab.
Auswertung
Über einen linearen Fit unter Berücksichtigung der x-Fehler wurden mittels der Software OriginPro 2017G die Nulldurchgänge der in Abb. 4 gezeigten Kennlinien möglichst präzise bestimmt. Für die Fits wurden dabei nur die in Abb. 5 und 6 gezeigten Werte berücksichtigt, bei denen der Betrag der Stromstärke bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left|I\right| < 250 ~\mathrm{pA}} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{1}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{2}} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left|I\right| < 100 ~\mathrm{pA}} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{3}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_{4}} lag. Die Annahme eines linearen Verlaufs stellt dabei eine Näherung dar, die aber im Hinblick auf die Messwerte (s. Abb. 5 und 6) legitim scheint. Aus den ausgegebenen Fitparametern wurden folgende Gegenspannungen errechnet:
| Wellenlänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda / \mathrm{nm}} |
zugehörige Frequenz
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f/ \mathrm{THz}} |
Gegenspannung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{G,0} / \mathrm{V}} |
|---|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 405\pm10} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 7,40\pm0,18} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,12\pm0,18} |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 436\pm10} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 6,88\pm0,16} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,94\pm0,15} |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 546\pm10} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 5,49\pm0,10} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,45\pm0,11} |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 580\pm10} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 5,17\pm0,09} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,36\pm0,11} |
Die Unsicherheit ergab sich dabei per Gauß'scher Fehlerfortpflanzung aus den von Origin angegebenen Unsicherheiten der Fitparameter.
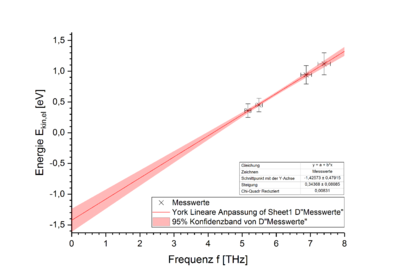
Diese Gegenspannungen entsprechen der maximalen kinetischen Energie der durch den Photoeffekt ausgelösten Elektronen (angegeben in Elektronenvolt: eV). Werden diese Energien über der nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f=\frac{c}{\lambda}} berechneten Frequenz der eingestrahlten Photonen aufgetragen, ergibt sich ein einer Gerade sehr nahe liegender Verlauf, wie in Abb. 7 ersichtlich. Für diese vier Werte wurde ein linearer Fit unter Berücksichtigung der x-Fehler durchgeführt. Der so ermittelte Anstieg der Geraden entspricht dem Plank'schen Wirkungsquantum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} . Hierbei ergab sich ein Wert von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h=3,43\pm0,81\cdot 10^{-15}~\mathrm{eVs}=5,5\pm1,3\cdot 10^{-34}~\mathrm{Js}} . Der Literaturwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{Lit}=6,626\cdot 10^{-34}~\mathrm{Js}} liegt dabei noch innerhalb des einfachen Fehlerintervalls.
Die ermittelte Unsicherheit ist mit einem relativem Wert von über 20% sehr hoch. Wie aus Abb. 7 ersichtlich wird, liegt die Ausgleichsgerade deutlich näher an den Messwerten, als durch ihre Unsicherheit suggeriert wird und auch der Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \chi^2} -Wert fällt mit 0,008 gering aus. Ginge man folgerichtig von einem kleineren zufälligen Fehler aus, würde jedoch der Referenzwert nicht mehr innerhalb des Fehlerintervalls liegen. Dies kann verschiedene Ursachen haben, in diesem Fall könnte am ehesten ein systematischer Fehler vermutet werden. Das der ermittelte Wert darüber hinaus nicht größer sondern kleiner als der erwartete ist, könnte dabei an dem schon erwähnten Austritt von Elektronen aus der Anode liegen. Da für diese Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_G} als Beschleunigungsspannung wirkt, kommt es schon vor dem Versiegen des Photostroms von der Kathode zur Anode zu einem entgegengesetzt gerichteten Photostrom. Dadurch wird schon für eine Spannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U_{G,0}^{'} < U_{G,0}} eine Stromstärke von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I=0~\mathrm{A}} angezeigt, bei der noch Elektronen der Kathode die Anode erreichen. Diese Hypothese müsste allerdings noch experimentell überprüft werden, bisher stellt sie lediglich eine plausible Vermutung dar. Darüber hinaus darf nicht außer Acht gelassen werden, dass lediglich vier Punkte zur Regression beigetragen haben. Für eine bessere Beurteilung der Unsicherheiten wäre die Einbeziehung anderer Wellenlängen unumgänglich, was sich aber aufgrund der geringen Intensitäten (siehe Abb. 3) zumindest für die verwendete Hg-Lampe als schwierig erweist.
In Zusammenfassung kann beim Versuch über den Photoeffekt nach der Gegenfeldmethode das Plank'sche Wirkumsquatum über die auf Einstein zurückgehende Beziehung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=h f - W_A} ermittelt werden. Die dafür aufgenommenen Kennlinen erlauben, durch eine Regressionsrechnung die maximale Energie der ausgelösten Elektronen zu bestimmen. In dem hier beschriebenem Versuch wurde dies für vier annähernd monochromatische Spektrallinien einer Hg-Lampe durchgeführt. Eine Betrachtung des Photoeffekts in seinem historischen Kontext kann dabei einen Beitrag zu einem authentischem Experimentieren im Physikunterricht leisten.
Sicherheitshinweise
Eine Gefährdung für den Menschen ist bei der Durchführung dieses Versuchs zum Photoeffekt weniger zu befürchten. Eher schon könnte es zu einer Beschädigung der Geräte durch eine unsachgemäße Verwendung kommen. Insbesondere der Messverstärker sollte deshalb mit Vorsicht bedient und nicht überlastet werden. Nichtsdestotrotz ist ein direkter Blick in die Hg-Lampe zu vermeiden.
Literatur
- ↑ 1,0 1,1 Hallwachs, W. (1888a): Ueber den Einfluss des Lichtes auf electrostatisch geladene Körper. In: Ann. Phys. Chem. 269 (2), S. 301–312. DOI: 10.1002/andp.18882690206. Referenzfehler: Ungültiges
<ref>-Tag. Der Name „H88a“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ 2,0 2,1 Hallwachs, W. (1888b): Ueber die Electrisirung von Metallplatten durch Bestrahlung mit electrischem Licht. In: Ann. Phys. Chem. 270 (8A), S. 731–734. DOI: 10.1002/andp.18882700809.
- ↑ 3,0 3,1 Einstein, A. (1905): Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. In: Ann. Phys. 322 (6), S. 132–148. DOI: 10.1002/andp.19053220607.
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 4,6 Höttecke, D. & Rieß, F. (2015): Naturwissenschaftliches Experimentieren im Lichte der jüngeren Wissenschaftsforschung – Auf der Suche nach einem authentischen Experimentbegriff der Fachdidaktik. In: ZfDN 21 (1), S. 127–139. DOI: 10.1007/s40573-015-0030-z.
- ↑ Buxton, C. (2006): Creating contextually authentic science in a “low-performing” urban elementary school. In: J. Res. Sci. Teach. 43 (7), S. 695–721. DOI: 10.1002/tea.20105.
- ↑ Grehn, J. & Krause, J. (2007): Metzler Physik. 4. Aufl. Braunschweig: Schroedel.
- ↑ 7,0 7,1 Meyn, J.-P. (2011): Grundlegende Experimentiertechnik im Physikunterricht. München: Oldenbourg.
- ↑ Bormann, M. & Kuhn, W. (Hg.) (1996): Handbuch der experimentellen Physik. Sekundarbereich II; Ausbildung - Unterricht - Fortbildung. Köln: Deubner.
Siehe auch
Bestimmung von h durch die Gegenfeldmethode:
- Der Photoeffekt - Bestimmung von h durch die Gegenfeldmethode (im Entstehen),
- Didaktischer Wert von Berechnungen der Messunsicherheit am Beispiel eines Versuchs zum Photoeffekt (im Entstehen),
Alternative Bestimmung von h durch Umkehrung des Photoeffekts: