Didaktischer Wert von Berechnungen der Messunsicherheit am Beispiel eines Versuchs zum Photoeffekt
| Didaktischer Wert von Berechnungen der Messunsicherheit am Beispiel eines Versuchs zum Photoeffekt | |
 Versuchsaufbau zum Photoeffekt | |
| Kurzbeschreibung | |
|---|---|
| Nutzen von stark von Referenzwerten abweichenden Messergebnissen zur Diskussion von Messunsicherheiten | |
| Kategorien | |
| Atom- und Kernphysik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sekundarstufe II |
| Basiskonzept: | Wechselwirkung, Energie |
| Sonstiges | |
| Durchführungsform | Demonstrationsexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittelschwer |
| Informationen | |
| Name: | Anna-Lena Neidhardt |
| Kontakt: | neidhaan@hu-berlin.de |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Der äußere photoelektrische Effekt (kurz: Photoeffekt) und dessen Deutung durch Albert Einstein sind wesentliche Schritte zur Erkenntnis der Teilcheneigenschaften des Lichtes und damit des Welle-Teilchen-Dualismus. Während beispielsweise das Doppelspaltexperiment mit Welleneigenschaften des Lichtes gut erklärt werden kann, stößt das Wellenmodell zur Erklärung des Fotoeffekts an seine Grenzen, was Einstein in einem Beitrag der Fachzeitschrift "Annalen der Physik" überzeugend darlegt. (Siehe Einstein[1], S.132 f., S. 144 ff.) Im Folgenden sollen der Aufbau und die Durchführung eines Experiments zur Bestimmung des Planckschen Wirkungsquantums mithilfe des Photoeffekts dargestellt werden. Auch wenn das fachliche Ziel der Bestimmung einer Naturkonstanten hier nicht erreicht wurde, kann der Versuch dennoch durchaus eingesetzt werden um darauf einzugehen, welche Rolle Messunsicherheiten bei großen Abweichungen ermittelter Größen von Literaturwerten spielen.
Inhaltsverzeichnis
Didaktischer Teil
Messunsicherheiten sind kein notwendiges Übel, das Studenten wie Schüler auf sich nehmen müssen, um gewissen Anforderungen zu genügen. Vielmehr sind sie ein wichtiger Bestandteil der Erkenntnisgewinnung in den Naturwissenschaften, insbesondere in der Physik. Erst durch Betrachtung von Messunsicherheiten können Experimente auf ihre Genauigkeit überprüft, systematische Messabweichungen identifiziert und im Idealfall beseitigt und unterschiedliche Messmethoden vergleichbar gemacht werden. Weil dieses Thema ein so prägender Teil der Physik ist, ist es vonnöten, dass den Schülerinnen und Schülern im Unterricht nicht nur die Vorgehensweise zu Berechnung von Unsicherheiten beigebracht, sondern auch deren Wert und Wichtigkeit in den Naturwissenschaften vermittelt wird. Zum Beispiel ist es wichtig zu begreifen, dass Messwerte, die von Literaturwerten abweichen, nicht automatisch auf eine fehlerhafte Messung zurückzuführen sind. Erst durch die Ermittlung und Auswertung von Messunsicherheiten lässt sich feststellen, ob es sich um eine zufällige oder systematische Abweichung handelt. Eine zufällige Messabweichung entsteht dadurch, dass Einflussgrößen "unvorhersehbare[n] oder stochastische[n] zeitliche[n] und räumliche[n] Schwankungen" (vgl. Hellwig[2] (2012), S. 63) unterliegen. Sie sind bei jeder Messung je nach Genauigkeit der Messmethoden unterschiedlich stark vorhanden. Ihr Erwartungswert ist Null. Eine systematische Messabweichung entsteht, wenn Einflussgrößen auftreten, die systematisch auf die Messung einwirken. Bekannte systematische Messabweichungen (z.B. Offset) können mit den Messergebnissen verrechnet werden, haben also keinen Einfluss auf die Genauigkeit der Messung. Unbekannte systematische Abweichungen hingegen können unvorhergesehene Effekte bewirken, die das Ergebnis stark beeinflussen. Es gilt, diese Einflüsse zu erkennen und im Idealfall möglichst zu beseitigen.
In der Sekundarstufe I wird die Physik noch viel qualitativ unterrichtet. Auch bei Themen, innerhalb derer Messungen und Berechnungen durchgeführt werden, geht es vor allem um das Verstehen bestimmter Zusammenhänge, nicht primär um die Genauigkeit der gemessenen und errechneten Werte. Entsprechend stehen hier nicht Messunsicherheiten, sondern andere Aspekte der "Natur der Naturwissenschaften" wie zum Beispiel das Thema der Modellvorstellungen im Vordergrund. Ein Beispiel hierfür sind elektrische Stromkreise. Zwar können Messungen und Berechnungen von Stromstärke, Spannung und Widerstand durchgeführt werden, vorrangig geht es aber um das Verständnis von Reihen- und Parallelschaltungen. (Bei Interesse siehe Beitrag von Niklas Sturm, Vortrag am 24.11.2016.)
In der Sekundarstufe II erhalten quantitative Betrachtungen eine höhere Bedeutung. Deshalb sollte den Schülerinnen und Schülern im Zuge des Unterrichtens von "Nature of Science" der Umgang mit Messunsicherheiten und Messabweichungen beigebracht werden. Die Schülerinnen und Schüler sollten anhand gegebener Ergebnisse und deren Messunsicherheiten in der Lage sein, zu beurteilen, ob Abweichungen von Referenzwerten auf mangelnde Genauigkeit der Messung oder auf ein fehlerhaftes Vorgehen bzw. unerkannte systematische Einflüsse zurückzuführen sind.
Zwar ist das eigentliche Ziel des dargestellten Aufbaus die Bestimmung des Planckschen Wirkungsquantums h. Doch auch wenn hier in dieser Hinsicht die Ergebnisse des Versuchs ziemlich enttäuschend sind, eignet er sich stattdessen gut zur Thematisierung des wichtigen Themas der Messunsicherheiten.
Versuchsanleitung
Aufbau
Der Aufbau des Versuchs lässt sich in den optischen und den elektrischen Aufbau gliedern. Der optische Aufbau soll gewährleisten, dass das Lichtbündel der Halogenlampe die Photokathode beleuchtet ohne auf den Anodenring zu treffen. Der elektrische Aufbau dient der Einstellung der Gegenspannung und der Messung der Photostromstärke.
Optischer Aufbau
Es werden die folgenden Geräte benötigt:
- optische Bank (1m) inklusive 6 Optikreitern
- Halogenlampe (Leybold 45064) mit passendem Netzgerät (Phywe Stelltrafo 13531)
- zwei Lochblenden (Leybold)
- schwarze Röhre
- Linse (konvex, Brennweite 150mm)
- Interferenzfilter für verschiedene Wellenlängen: 350nm, 369nm, 375nm, 405nm, 436nm, 491nm, 546nm, 580nm, 656nm, 671nm
- Halterung für Interferenzfilter
- Fassung der Fotozelle (hier: aus Styropor)
- Fotozelle (Kathodenmaterial: Cäsium-Antimon)
- schwarze Alufolie
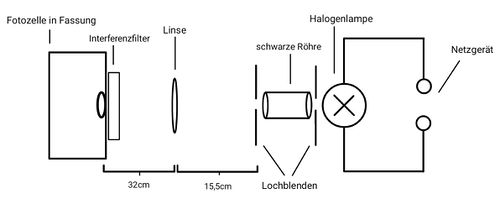
Die Geräte werden aufgebaut, wie in der nebenstehenden Abbildung (Abb. 1) (nicht maßstabsgetreu) dargestellt. Mit der Alufolie wird die Konstellation von Halogenlampe, Lochblende und Röhre so abgedeckt, dass möglichst wenig Licht nach außen dringt. Da in diesem Aufbau eine behelfsmäßige Fassung aus Styropor verwendet wurde, war auch hier eine Abdeckung mit schwarzer Alufolie sinnvoll, um den Anteil des in die Fotozelle gestreuten Lichts möglichst gering zu halten.
Erläuterung: Die beiden Lochblenden und die Röhre dienen der Fokussierung des Lichtes derart, dass das Lichtbündel möglichst parallel zur optischen Achse auf die Linse trifft.
Hinweis: Die Längenangaben für den Abstand der Linse zur zweiten Blende bzw. zur Fotozelle können variieren. Die Linse sollte so positioniert werden, dass das Lichtbündel auf die Photokathode fokussiert wird, ohne auf den Anodenring zu treffen. Dies ist notwendig, um Störströme zu vermeiden, die durch einen ungewollten Photoeffekt auf der Anode entstehen können.
Elektrischer Aufbau
Zusätzlich zur oben aufgeführten Fotozelle, werden für den elektrischen Aufbau diese Geräte benötigt:
- Netzgerät zur Regelung der Gegenspannung (Voltcraft Labornetzgerät)
- Messverstärker (Phywe 7539)
- zwei digitale Messgeräte (PeakTech)
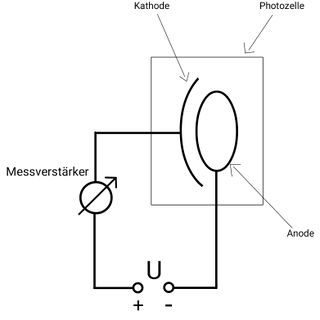
Die Geräte werden gemäß der nebenstehenden Abbildung (Abb. 2) aufgebaut. Die beiden digitalen Messgeräte werden zur Messung der Stromstärke am Messverstärker und zur genaueren Bestimmung der Gegenspannung am Netzgerät angeschlossen.
Durchführung
Ziel und allgemeine Vorgehensweise
Ziel der Messreihe ist es, den linearen Zusammenhang zwischen der Frequenz des einfallenden Lichtes und der zugehörigen maximalen kinetischen Energie der herausgeschlagenen Elektronen zu erfassen und aus der Steigung der Ausgleichsgeraden das Plancksche Wirkungsquantum zu bestimmen. Die maximale kinetische Energie der Elektronen bei einer gewissen Frequenz lässt sich über die ermittelte zugehörige Grenzspannung (Spannung bei der gerade kein Fotostrom mehr vorhanden ist) berechnen.
Eine oft verwendete Methode zur Bestimmung der Grenzspannung zu einer Wellenlänge ist es, so lange die Gegenspannung zu erhöhen, bis mit dem Messverstärker kein Fotostrom mehr messbar ist und ebendiese Spannung zu notieren. Da die Fotostromstärke aber quadratisch mit steigender Gegenspannung sinkt, bei verschwindender Stromstärke also auch die entsprechende Steigung Null wird, liefert diese Methode keine allzu genauen Messwerte. Stattdessen ist es möglich, mehrere Stromstärke-Spannungs-Wertepaare aufzunehmen und die Wurzel aus der Stromstärke über die Spannung aufzutragen. Durch eine lineare Ausgleichsfunktion kann man dann die Nullstelle und damit den Wert für die Grenzspannung ermitteln. (siehe Meyn[3] (2013), S.132 f.)
Vorkehrungen
Die Messung sollte in einem möglichst abgedunkelten Raum durchgeführt werden, um zu vermeiden, dass zusätzliches Licht auf die Photokathode trifft.
Um ein über die Zeit möglichst gleichbleibendes Spektrum zu gewährleisten, ist es zu empfehlen, die Halogenlampe etwa eine Minute vor Beginn der Messungen anzuschalten. Außerdem sollte sie beim Wechseln der Interferenzfilter nicht ausgeschaltet, sondern lediglich abgedunkelt werden.
Zu Beginn jeder Messreihe zu einer bestimmten Frequenz ist keine Gegenspannung angelegt.
Einzelne Messreihen
Zunächst wird der Interferenzfilter in der Halterung direkt vor der Fassung der Fotozelle angebracht. Beginnend bei einer Spannung von wird die Spannung in bzw. -Schritten bis auf erhöht und die Stromstärke notiert. In der Regel wurde hier eine zusätzliche Messung bei genommen. Bei besonders niedrigen Stromstärken wurde die Messung frühzeitig abgebrochen.
Ergebnisse
Die folgende Tabelle beinhaltet alle aufgenommenen Messwerte.
| , | , | , | , | , | , | , | , | , | , | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,107 | 0,039 | 0,340 | 0,910 | 0,957 | 1,123 | 0,921 | 0,934 | 0,379 | 0,281 |
| 0,10 | 0,109 | 0,037 | 0,329 | 0,891 | 0,950 | 1,116 | ||||
| 0,20 | 0,096 | 0,035 | 0,320 | 0,884 | 0,929 | 1,101 | 0,884 | 0,903 | 0,353 | 0,271 |
| 0,30 | 0,094 | 0,038 | 0,321 | 0,874 | 0,905 | 1,083 | ||||
| 0,40 | 0,084 | 0,036 | 0,317 | 0,852 | 0,896 | 1,064 | 0,856 | 0,857 | 0,324 | 0,252 |
| 0,50 | 0,085 | 0,036 | 0,299 | 0,831 | 0,871 | 1,049 | ||||
| 0,60 | 0,089 | 0,032 | 0,294 | 0,805 | 0,857 | 1,027 | 0,811 | 0,817 | 0,307 | 0,208 |
| 0,70 | 0,079 | 0,028 | 0,282 | 0,789 | 0,843 | 1,008 | ||||
| 0,80 | 0,077 | 0,020 | 0,276 | 0,766 | 0,815 | 0,988 | 0,759 | 0,767 | 0,280 | 0,188 |
| 0,90 | 0,069 | 0,018 | 0,263 | 0,750 | 0,793 | 0,968 | ||||
| 1,00 | 0,065 | 0,013 | 0,263 | 0,722 | 0,764 | 0,947 | 0,706 | 0,719 | 0,259 | 0,160 |
| 1,10 | 0,062 | 0,255 | 0,704 | 0,738 | 0,932 | |||||
| 1,20 | 0,063 | 0,241 | 0,681 | 0,716 | 0,908 | 0,653 | 0,658 | 0,230 | 0,141 | |
| 1,30 | 0,060 | 0,231 | 0,664 | 0,691 | 0,891 | |||||
| 1,40 | 0,053 | 0,225 | 0,632 | 0,670 | 0,854 | 0,615 | 0,618 | 0,207 | 0,121 | |
| 1,50 | 0,060 | 0,212 | 0,614 | 0,652 | 0,827 | |||||
| 1,60 | 0,049 | 0,211 | 0,600 | 0,631 | 0,793 | 0,577 | 0,579 | 0,180 | 0,101 | |
| 1,70 | 0,052 | 0,205 | 0,579 | 0,609 | 0,758 | |||||
| 1,80 | 0,048 | 0,192 | 0,561 | 0,593 | 0,727 | 0,541 | 0,540 | 0,158 | 0,082 | |
| 1,90 | 0,046 | 0,184 | 0,544 | 0,573 | 0,695 | |||||
| 2,00 | 0,040 | 0,177 | 0,525 | 0,555 | 0,668 | 0,502 | 0,504 | 0,138 | ||
| 2,50 | 0,027 | 0,128 | 0,437 | 0,463 | 0,542 | 0,411 | 0,405 | 0,081 |
Auswertung
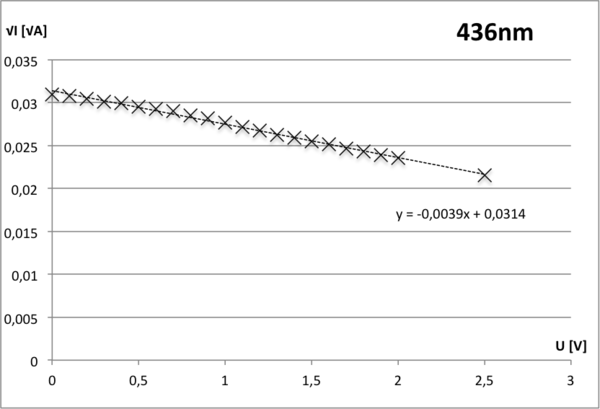
Hier wird am Beispiel einer Wellenlänge von 436nm die Auswertung einer einzelner Messreihe vorgenommen. Wie oben beschrieben, wird die Wurzel der Stromstärke über die Spannung aufgetragen. Im Diagramm (Abb. 3) ist der lineare Zusammenhang deutlich zu erkennen. Nutzt man ein Tabellenkalkulationsprogramm (z.B. Excel), kann man sich die Ausgleichsgerade und deren Funktion anzeigen lassen.
| 0,00 | 0,957 | 0,0309 |
| 0,10 | 0,950 | 0,0308 |
| 0,20 | 0,929 | 0,0305 |
| 0,30 | 0,905 | 0,0301 |
| 0,40 | 0,896 | 0,0299 |
| 0,50 | 0,871 | 0,0295 |
| 0,60 | 0,857 | 0,0293 |
| 0,70 | 0,843 | 0,0290 |
| 0,80 | 0,815 | 0,0285 |
| 0,90 | 0,793 | 0,0282 |
| 1,00 | 0,764 | 0,0276 |
| 1,10 | 0,738 | 0,0272 |
| 1,20 | 0,716 | 0,0268 |
| 1,30 | 0,691 | 0,0263 |
| 1,40 | 0,670 | 0,0259 |
| 1,50 | 0,652 | 0,0255 |
| 1,60 | 0,631 | 0,0251 |
| 1,70 | 0,609 | 0,0247 |
| 1,80 | 0,593 | 0,0244 |
| 1,90 | 0,573 | 0,0239 |
| 2,00 | 0,555 | 0,0236 |
| 2,50 | 0,463 | 0,0215 |
Mithilfe der Ausgleichsgeraden und deren Formel der Form (mit m: Steigung; t: y-Achsenabschnitt) lässt sich die Grenzspannung berechnen als . Im Fall von 436nm ergibt sich also:
Analog muss nun die Grenzspannung für alle betrachteten Wellenlängen ermittelt werden. Mit den oben aufgeführten Werten ergibt sich folgende Tabelle, die außerdem die den Wellenlängen entsprechenden Frequenzen enthält:
| 8,57 | 350 | 5,15 |
| 8,12 | 369 | 2,68 |
| 7,99 | 375 | 6,93 |
| 7,40 | 405 | 8,05 |
| 6,88 | 436 | 8,05 |
| 6,11 | 491 | 8,60 |
| 5,49 | 546 | 7,59 |
| 5,17 | 580 | 7,19 |
| 4,57 | 656 | 4,83 |
| 4,47 | 671 | 4,33 |
Schon bei Betrachtung dieser Werte kann man vermuten, dass sich eine lineare Ausgleichsfunktion selbst bei sehr groben Fehlerabschätzungen nicht im Intervall der Messunsicherheiten finden wird. Dennoch ist es wichtig, die Messreihe nicht sofort zu verwerfen, sondern die Messunsicherheiten mit allen relevanten Einflussfaktoren zu berechnen. Wie oben erläutert, kann man nämlich erst dann feststellen, ob der Aufbau an sich ungeeignet ist, weil die Messunsicherheiten im Vergleich zu den Messwerten sehr groß werden, oder ob die Messung fehlerhaft durchgeführt wurde, bzw. eines der Geräte nicht funktionstüchtig ist, weil die Literaturwerte nicht in den errechneten Messunsicherheiten liegen.
Zunächst werden die einzelnen Unsicherheiten, die bei der Messung der Stromstärke eine Rolle spielen, aufgeführt:
| Gerät | Unsicherheit |
|---|---|
| Messverstärker | 0,01mA |
| Spannungsmessgerät | 0,01V |
| Strommessgerät | 0,001mA |
| Interferenzfilter | Je nach Filter: Schätzung über Halbwertsbreite |
Eine Hürde bei der Fortpflanzung der Unsicherheiten ist die Ermittlung der Grenzspannung über die Ausgleichsgerade. Die Vorgehensweise hierbei und bei anderen Fehlerberechnungen sind einer Dissertation entnommen. (Siehe Hellwig [2] (2012), S.90 f., S. 99 f.)
Hier wird die Vorgehensweise am Beispiel einer Wellenlänge von 436nm nachvollzogen:
Die Halbwertsbreite des Interferenzfilters für eine Wellenlänge von 436nm beträgt 10,5nm. Daraus kann man einen prozentualen Fehler von schätzen. Für die Berechnung der Unsicherheit der Ausgleichsgeraden ist es nötig, dass allen Werten die selbe Unsicherheit zugeordnet wird. Um eine Unterschätzung der Messunsicherheiten zu vermeiden, werden hier bei der Umrechnung von prozentualen in absolute Fehler immer die größten gemessenen Werte mit den prozentualen Fehlern verrechnet.
Es ergibt sich für die gemessenen Stromstärken:
Da nicht die gemessenen Stromstärken über die Spannung aufgetragen wurden, sondern jeweils die Wurzel daraus, muss eine Fehlerfortpflanzung durchgeführt werden.
Die Unsicherheit des y-Achsenabschnitts t berechnet sich als:
Und die Unsicherheit der Steigung m als:
Wegen des Zusammenhangs muss die Unsicherheit für die ermittelte Grenzspannung folgendermaßen errechnet werden:
Analog wird diese Rechnung für alle Wellenlängen durchgeführt. Weil am Ende der Zusammenhang von Frequenz und Energie dargestellt werden soll, ist in der Tabelle zusätzlich die der jeweiligen Wellenlänge entsprechenden Frequenz angegeben.
| 350 | 8,65 | 9 | 0,0257 | 0,0000104 | 0,000504 | 0,000203 | 0,000161 | 0,443 |
| 369 | 8,12 | 7 | 0,0190 | 0,0000101 | 0,000807 | 0,000455 | 0,000769 | 0,871 |
| 375 | 7,99 | 8 | 0,0213 | 0,0000124 | 0,000336 | 0,000135 | 0,000107 | 0,278 |
| 405 | 7,40 | 11 | 0,0272 | 0,0000276 | 0,000443 | 0,000178 | 0,000141 | 0,302 |
| 436 | 6,88 | 10,5 | 0,0241 | 0,0000252 | 0,000407 | 0,000164 | 0,000130 | 0,272 |
| 491 | 6,11 | 12 | 0,0244 | 0,0000292 | 0,000435 | 0,000175 | 0,000139 | 0,300 |
| 546 | 5,49 | 5,5 | 0,0101 | 0,0000137 | 0,000226 | 0,000119 | 0,0000888 | 0,161 |
| 580 | 5,17 | 10 | 0,0172 | 0,0000189 | 0,000310 | 0,000164 | 0,000122 | 0,211 |
| 656 | 4,57 | 8 | 0,0122 | 0,0000111 | 0,000284 | 0,000150 | 0,000112 | 0,138 |
| 671 | 4,47 | 7,5 | 0,0112 | 0,0000105 | 0,000314 | 0,000177 | 0,000150 | 0,172 |
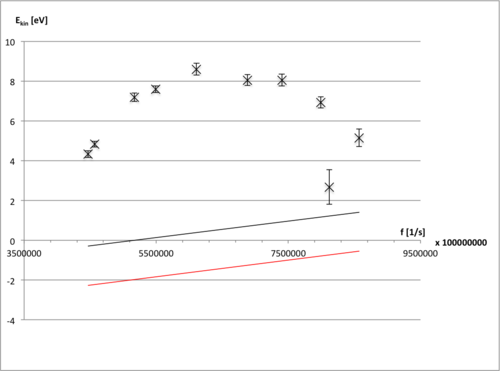
Die maximale kinetische Energie der Elektronen ist gleich der elektrischen Feldenergie, bei der gerade kein Fotostrom mehr fließt. Deshalb entsprechen die gemessenen Werte der Spannung genau den Werten der kinetischen Energie in eV. Trägt man nun die relevanten Daten mit ihren Messunsicherheiten in ein Diagramm ein (siehe Abb. 4), wird klar, dass mit der Messung etwas nicht in Ordnung war. Zum Vergleich sind hier auch die entsprechenden Kennlinien des Kathodenmaterials abgebildet.
Offensichtlich liegt eine nicht korrigierte systematische Messabweichung vor. Selbst, wenn die Messunsicherheiten um ein Vielfaches größer wären, als die angenommenen, wären die gemessenen Werte noch immer außerhalb des Bereiches, in dem sie sein sollten. Diese kann die folgenden Gründe haben:
- Die verwendete Fotozelle ist nicht mehr funktionstüchtig.
- Der optische Aufbau wurde nicht so optimiert, dass kein Licht auf die Anode der Fotozelle trifft.
- Der benutzte, recht alte Messverstärker, zu dem keine Gebrauchsanweisung vorlag, wurde nicht richtig verwendet.
Die recht geringe Intensität des Lichts der Halogenlampe (zusätzlich verringert durch die Interferenzfiler) bei einzelnen Wellenlängen trägt zwar möglicherweise auch zur Abweichung bei, kann aber nicht der wichtigste Faktor sein, weil alle Werte sehr stark von den Referenzwerten abweichen.
Trotz der nicht zufriedenstellenden physikalischen Ergebnisse, eignet sich dieser Aufbau gut zur Beantwortung der Frage, welche Rolle Messunsicherheiten bei großen Abweichungen von Referenzwerten spielen. In jedem Fall ist eine Thematisierung dieser Frage im Physikunterricht der Oberstufe sehr zu empfehlen.
Sicherheitshinweise
Selbstverständlich ist wie bei jedem anderen elektrischen Aufbau darauf zu achten, dass alle Kabel ausreichend isoliert sind. Die Geräte sollten nicht länger als nötig in Betrieb gehalten werden. Weitere spezielle Sicherheitsvorkehrungen sind nicht zu treffen.
Literatur
- ↑ Einstein, A. (1905): Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt; Verlag von Johann Abrosius Barth, Leipzig, verfügbar unter [1] [24.03.2017]
- ↑ 2,0 2,1 Hellwig, J. (2012): Messunsicherheiten verstehen - Entwicklung eines normativen Sachstrukturmodells am Beispiel des Unterrichtsfachs Physik; Ruhr-Universität Bochum
- ↑ Meyn, J. (2013): Grundlegende Experimentiertechnik im Physikunterricht; 2. Auflage, Oldenburg Verlag





![{\displaystyle U[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abd79e2af03e6bd5bd15d098e12fb6a0ec46128f)
![{\displaystyle I[mA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e859a48dd70fdf6ea22b6f1fd46cad2a429dd5d)










![{\displaystyle {\sqrt {I}}[{\sqrt {A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9d0e22ca02bbbdb7c7201b56ae1e7368e92af6d)



![{\displaystyle f[10^{14}{\frac {1}{s}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/013ad57c0c677eaef9d981d03000ed6dee8246f8)
![{\displaystyle \lambda [nm]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f94ac477220ecfc8348a1e0c802d26e2d7433bc)
![{\displaystyle U_{0}[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48d027aa59af31c40e3e2aea94c08ec546948ce2)







![{\displaystyle Halbwertsbreite[nm]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fde72a76061efcb94408994d3864d7ec53b9c68)