Westphalsche Waage - Temperaturabhängigkeit der Dichte von Flüssigkeiten
| Westphalsche Waage - Temperaturabhängigkeit der Dichte von Flüssigkeiten | |
| Westphalsche Waage Modell Johann Hammer Leipzig 1 | |
| Kurzbeschreibung | |
|---|---|
| Mit der Westphalschen Waage wird die Dichte von Flüssigkeiten bestimmt. Die Messgenauigkeit liegt bei 0,0005g/cm³. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 7, Klasse 8, Klasse 9, Klasse 10 |
| Basiskonzept: | System, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Schülereinzelexperiment, Schülergruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Carsten Ehlert |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Daniel Zechlin |
Die Westphalsche Waage ist eine ungleicharmige Hebelwaage zur Dichtebestimmung von Flüssigkeiten. Ein Senkkörper wird in die zu untersuchende Flüssigkeit getaucht. Unter Anwendung des Archimedischen Prinzips kann der Dichtewert nach Einpendeln der Waage durch Auflegen von Wägestücken bis auf vier Dezimalstellen genau abgelesen werden.
Der Versuch eignet sich unter anderem für den Erkenntnisgewinn im Bereich der Durchführung von Messungen und im Umgang mit Messwertergebnissen.
Inhaltsverzeichnis
Didaktischer Teil
Motivation
Der sachgerechte Umgang mit Messwerten ist allgemein von großer Bedeutung. Beobachtung und Messung sind naturwissenschaftliche Methoden zur Erkenntnisgewinnung. Natürliche Phänomene oder technische Effekte können hierdurch erfasst werden. Der Begriff „Messfehler" ist bei SchülerInnen emotional negativ konnotiert (Heinicke, Glomski, Priemer & Rieß.). Auch bei der Verwendung des Begriffs „Messunsicherheit“ wie er von Heinicke et al. empfohlen wird, versuchen SchülerInnen häufig, ihre Messwerte so anzupassen, dass sie möglichst nah an den Werten liegen, die sie aus der Literatur kennen oder dort recherchieren können. Eine Fehlerabschätzung wird häufig vernachlässigt, der Fehler wird korrigiert oder wegdiskutiert (Heinicke et al.).
Didaktischer Wert und Didaktische Ziele des Versuchs
Jede Messung ist mit Messfehlern behaftet (Hellwig 2012, nach Miller & Osborne 1998). Die Kenntnis über die Messunsicherheit ist wesentlich zur Bewertung der Güte der Messung (Heinicke et al.). Über dieses Kriterium werden in der Wissenschaft verschiedene Forschungsergebnisse eingeschätzt. Neben naturwissenschaftlichen Berufen ist ein Verständnis über Messunsicherheiten auch in alltäglichen Entscheidungssituationen wichtig (Hellwig, 2012). Daher sollten sich auch SchülerInnen mit der Thematik Messfehler auseinandersetzen. Hellwig (2012) weist darauf hin, dass Messunsicherheiten in vielen Rahmenlehrplänen und auch den deutschen Bildungsstandards nicht explizit benannt werden. Es gebe aber entsprechende Bezüge, vor allem im Kompetenzbereich Erkenntnisgewinnung, die die Auseinandersetzung mit der Thematik Messunsicherheit als notwendig erachten lassen. Heinicke et al. erläutern weiterhin, dass „[e]ine explizite Thematisierung von Messunsicherheiten im Physikunterricht […] einen entscheidenden Beitrag zur Vermittlung einer adäquaten Sichtweise über die naturwissenschaftliche Arbeitsweise und Interpretation experimenteller Ergebnisse leisten [könnte]“ (Heinicke et al., S. 33).
Der hier vorgestellte Versuch dient dem Erkenntnisgewinn im Bereich der Durchführung von Messungen, der Auswertung sowie der Interpretation der Messwertergebnisse und Abschätzung der Messunsicherheit. Die SchülerInnen werden an das Verständnis von Messergebnissen als Werteintervalle anstatt bloßer Zahlenwerte herangeführt. Die bewusst durchgeführte Fehlerabschätzung bei den eigenen Messwerten schult die kritische Auseinandersetzung mit Messdaten generell.
Eingliederung in den Unterricht
Wie oben beschrieben, ist der Versuch geeignet für den Erkenntnisgewinn im Bereich Messen. Laut den Rahmenlehrplänen (Berlin) für die Sekundarstufe I (RLP Sek I) und für die gymnasiale Oberstufe (RLP gym) sollen die SchülerInnen „beim Experimentieren naturwissenschaftliche Beobachtungsgeräte und Messgeräte ziel- und sachgerecht ein[setzen], […] Messungen physikalischer Größen durch[führen] und […] sie mit angemessenen mathematischen Methoden aus[werten]“ (RLP Sek I, S.21, vergleiche hierzu auch RLP gym S. 10).
Insbesondere im Wahlpflichtfach Physik in der Sekundarstufe I kann das Thema Größen messen und Messfehler betrachten vertieft behandelt werden. Folgende Kompetenzen können dabei gefördert werden: „Die Schülerinnen und Schüler […] - erkennen Messfehlerursachen und geben Verfahren zur Minimierung an […] - schätzen die Messgenauigkeit, führen Messungen durch und werten sie statistisch aus“ (RLP Sek I, S. 71).
Mit thematischem Bezug zur physikalischen Größe Dichte kann der Versuch im Jahrgang 7/8 im Pflichtbereich Mechanik – Schwimmen, Schweben, Sinken (P1 7/8) durchgeführt werden. Folgende Kompetenzen können dabei neben den bereits oben genannten gefördert werden: „Die SchülerInnen und Schüler erstellen Protokolle und unterscheiden bei Versuchsprotokollen deutlich zwischen Durchführung, Beobachtung, Auswertung und Erklärung“ (RLP Sek I, S. 25).
Methode
Es empfiehlt sich, den Versuch als Schülerversuch in Kleingruppen (arbeitsgleicher oder arbeitsteiliger Gruppenunterricht) von zwei bis vier SchülerInnen oder in Lernzirkeln durchführen zu lassen. Die SchülerInnen haben hierdurch die Möglichkeit des selbstbestimmten, gemeinsamen und kreativen Handelns und können mehr Eigenaktivität und Eigenverantwortung übernehmen und somit mehr Sach- und Selbstkompetenz entwickeln. Die Lehrperson tritt in den Hintergrund. Zusätzlich werden Fähigkeiten wie Kommunikationsfähigkeit und Kooperationsfähigkeit gefördert (Kircher, Girwidz & Häußler).
Der Versuch eignet sich sehr gut für die Kleingruppenarbeit, da der Aufbau und die Handhabung der Westphalschen Waage sehr einfach sind und hierbei keine weiteren Hilfen durch die Lehrkraft benötigt werden. Eine Beschreibung als Handreichung reicht aus.
Versuchsanleitung
Aufbau
Für den Versuch wird eine Westphalsche Waage Modell Johann Hammer Leipzig 1 verwendet. Folgende Materialien werden benötigt (siehe auch Abbildung 1 und 2):
- Stativfuß mit Libelle (1)
- Aufsatz mit ungleicharmiger Hebelwaage (2)
- Draht mit Senkkörper mit integriertem Thermometer (3)
- Reiter (Wägestücke): 2 x 5,000g, 1 x 0,500g, 1 x 0,050g, 1 x 0,005g (4)
- Pinzette (5)
- Glaszylinder für zu untersuchende Flüssigkeit (6)
- Wasserkocher oder Heizplatte
- Wasser
- Eiswürfel
- Thermometer
Der Aufsatz mit der Waage wird in den Stativfuß gesteckt und mit der Feststellschraube fixiert.
Die beiden Kalibrierungsschrauben am Stativfuß werden so eingestellt, dass die Libelle mittig
ausgerichtet ist (siehe Abbildung 3). Der Senkkörper wird an dem vorgesehenen Haken am Ende des
Lastarmes eingehängt. Die Waage sollte sich jetzt ins Gleichgewicht einpendeln, so dass die
Spitze des Waagebalkens der Spitze des Stativfußes genau gegenüber steht (siehe Abbildung 4).
Tut sie dies nicht, obwohl der Stativfuß richtig kalibriert ist, ist dies ein Hinweis auf eine fehlerhafte Justierung der Waage oder des Senkkörpers.
Durchführung
Vorbereitung
Es werden zwei Messreihen aufgenommen. In der ersten Messreihe wird warmes Wasser verwendet (30-40°C). Hierfür kann eine geringe Wassermenge im Wasserkocher oder auf der Heizplatte erhitzt werden. Der Glaszylinder wird mit der zu untersuchenden Flüssigkeit befüllt und der Senkkörper in den Glaszylinder eingetaucht. Mit der ersten Messung wird begonnen, sobald die Temperatur der Flüssigkeit unter 33°C liegt. Dies entspricht dem höchsten Messwert des Thermometers im Senkkörper.
In der zweiten Messreihe wird kaltes Wasser (<8°C) verwendet. Hierfür werden Eiswürfel in das Wasser gegeben bis die entsprechende Temperatur erreicht ist. Vor der ersten Messung sollen die Eiswürfel vollständig aufgelöst sein und das Wasser wird noch einmal durchgerührt. Der Glaszylinder wird mit der zu untersuchenden Flüssigkeit befüllt und der Senkkörper in diesen eingetaucht.
In beiden Messreihen werden im zeitlichen Verlauf Dichtebestimmungen durchgeführt, z.B. sobald sich die Temperatur um 2-3°C geändert hat. <br|>
Messung
Bei der Untersuchung von verschiedenen Flüssigkeiten ist darauf zu achten, dass die Eintauchtiefe des Senkkörpers bei allen Messungen gleich ist (halbe Länge des Drahtes, siehe Abbildung 5) um gleiche Auftriebskräfte des in die Untersuchungsflüssigkeit eingetauchten Drahtes zu gewährleisten. Dafür wird der Glaszylinder immer bis zum gleichen Füllstand befüllt (Markierung am Glaszylinder). Alternativ kann die Höhe des Stativs verändert werden. Der Kontakt des Senkkörpers oder Drahtes mit der Zylinderwand ist unbedingt zu vermeiden.
Durch Auflegen und Verschieben der Reiter auf die vorgesehenen und mit den Ziffern von 1 bis 9 versehenen Kerben am Lastarm (siehe Abbildung 5) wird die Waage nun ins Gleichgewicht gebracht. Dabei beginnt man mit dem größten Reiter am Haken. Befindet sich die Spitze des Waagebalkens oberhalb der Spitze des Ständers, wird der Reiter der Reihe nach auf die Einkerbung 9 bis 1 verschoben, bis sich die Spitze des Waagebalkens gerade unterhalb der Spitze des Ständers befindet (siehe oben Abbildung 4.). Die gleiche Prozedur wiederholt man mit dem jeweils nächstkleineren Reiter bis alle Reiter am Lastarm hängen (entsprechend der gewünschten Messgenauigkeit - kleinster Reiter entspricht Messgenauigkeit von 0,0005 g/cm³) und die Waage im Gleichgewicht ist. Das Volumen des Senkkörpers ist so gewählt (5 cm³), dass die Massen der Reiter/ Wägestücke in ihrem Zahlenwert 1/10, 1/100, und 1/1000 des in cm³ gemessenen Volumens des Senkkörpers entsprechen. Die Dichte der Flüssigkeit kann daher direkt an den Ziffern der Kerben, auf denen die Reiter liegen, abgelesen werden.
Beispiel: der Senkkörper befindet sich in der Flüssigkeit. Wenn die Waage im Gleichgewicht ist, sind die Reiter folgendermaßen verteilt: 1 großer Reiter in Kerbe 9, 1 mittlerer Reiter in Kerbe 4, 1 kleiner Reiter in Kerbe 6, der kleinste Reiter in Kerbe 8. Der gemessene Dichtewert beträgt somit 0,9468 g/cm³. Werden Wägestücke eines Gewichtes gar nicht aufgehängt, so entfällt auf diese Dezimalstelle eine Null.
Die Temperatur wird mit jeder Dichtebestimmung am Thermometer des Senkkörpers abgelesen.
<br|>
Beobachtung/ Ergebnisse
Die gemessenen Werte werden in einer Tabelle notiert.
<br|> Tab.1: Gemessene Dichtewerte in Abhängigkeit von der Temperatur. Die Werte wurden bei 23,3°C Raumtemperatur aufgenommen.
| ϑ in °C | ρ in g/cm³ |
|---|---|
| 4 | 0,9998 |
| 6 | 0,9999 |
| 8 | 1,0004 |
| 10 | 1,0003 |
| 12 | 1,0001 |
| 15 | 0,9999 |
| 21 | 0,9985 |
| 25 | 0,9969 |
| 27 | 0,9976 |
| 28 | 0,9978 |
| 30 | 0,9967 |
| 32 | 0,9959 |
Eine mögliche Beobachtung bei der Aufnahme der Messwerte ist die hohe Sensibilität der Waage. Selbst das Aufhängen und Verschieben des kleinsten Reiters ist deutlich sichtbar anhand einer veränderten Auslenkung des Hebelarmes. Nach jeder Veränderung der Reiter an der Waage benötigt diese eine gewisse Zeit, um sich wieder in die Ruhelage einzupendeln.
Beim Einhängen des Senkkörpers am Lastarm (siehe 3.1 Aufbau) hat sich die Waage nicht in den Gleichgewichtszustand eingependelt, sondern die Spitze des Hebelarmes stand etwas unter der Spitze des Stativfußes.
<br|>
Auswertung
Die ermittelten Dichtewerte sind noch mit einer Korrektur zu versehen, die z.B. den Einfluss des Luftauftriebs des Drahtes berücksichtigt. Die Korrekturwerte sind der Bedienungsanleitung entnommen und in Tabelle 2 aufgeführt. <br|> <br|> Tab. 2: Korrekturwerte für den Einfluss des Auftriebs des Drahtes und Flüssigkeitswulstes am Draht.
| Dichteangabe der Waage in g/cm³ | Korrektur in g/cm³ |
|---|---|
| 0,6 | 0,0002 |
| 0,7 | 0,0001 |
| 0,8 | 0,0000 |
| 0,9 | -0,0002 |
| 1,0 | 0,0000 |
| 1,1 | -0,0002 |
| 1,2 | -0,0003 |
| 1,3 | -0,0006 |
| 1,4 | -0,0008 |
| 1,5 | -0,0010 |
| 1,6 | -0,0012 |
| 1,7 | -0,0013 |
| 1,8 | -0,0015 |
| 1,9 | -0,0017 |
| 2,0 | -0,0019 |
<br|> Die Messunsicherheit der Waage ist mit 0,0005g/cm³ angegeben. Beim Ablesen der Temperatur wird eine Genauigkeit von einer halben Skaleneinheit angenommen. Nach Addition des Korrekturwertes und unter Berücksichtigung der Messunsicherheit ergibt sich die folgende Wertintervall-Tabelle.
Tab. 3: Wertintervalle der gemessenen Dichte in Abhängigkeit von der Temperatur. In der letzten Spalte wurden Werte aus Literaturangaben aufgenommen (aus Götz, Dahncke, Langensiepen: Handbuch des Physik-Unterrichts Sekundarbereich I).
| ϑ in ± Δϑ °C | ρ-Δρ in g/cm³ | ρ in g/cm³ | ρ+Δρ in g/cm³ | ρ (Literatur) in g/cm³ |
|---|---|---|---|---|
| 0 ± 0,5 | 0,9998 | |||
| 1 ± 0,5 | 0,9999 | |||
| 2 ± 0,5 | 0,9999 | |||
| 3 ± 0,5 | 1,0000 | |||
| 4 ± 0,5 | 0,9993 | 0,9998 | 1,0003 | 1,0000 |
| 5 ± 0,5 | 1,0000 | |||
| 6 ± 0,5 | 0,9994 | 0,9999 | 1,0004 | 0,9999 |
| 7 ± 0,5 | 0,9999 | |||
| 8 ± 0,5 | 0,9999 | 1,0004 | 1,0009 | 0,9998 |
| 9 ± 0,5 | 0,9998 | |||
| 10 ± 0,5 | 0,9998 | 1,0003 | 1,0008 | 0,9997 |
| 11 ± 0,5 | 0,9996 | |||
| 12 ± 0,5 | 0,9996 | 1,0001 | 1,0006 | 0,9995 |
| 13 ± 0,5 | 0,9994 | |||
| 14 ± 0,5 | 0,9992 | |||
| 15 ± 0,5 | 0,9994 | 0,9999 | 1,0004 | 0,9991 |
| 16 ± 0,5 | 0,9989 | |||
| 17 ± 0,5 | 0,9988 | |||
| 18 ± 0,5 | 0,9986 | |||
| 19 ± 0,5 | 0,9984 | |||
| 20 ± 0,5 | 0,9982 | |||
| 21 ± 0,5 | 0,9980 | 0,9985 | 0,9990 | 0,9980 |
| 22 ± 0,5 | 0,9978 | |||
| 23 ± 0,5 | 0,9975 | |||
| 24 ± 0,5 | 0,9973 | |||
| 25 ± 0,5 | 0,9964 | 0,9969 | 0,9974 | 0,9970 |
| 26 ± 0,5 | 0,9968 | |||
| 27 ± 0,5 | 0,9971 | 0,9976 | 0,9981 | 0,9965 |
| 28 ± 0,5 | 0,9973 | 0,9978 | 0,9983 | 0,9962 |
| 29 ± 0,5 | 0,9959 | |||
| 30 ± 0,5 | 0,9962 | 0,9967 | 0,9972 | 0,9957 |
| 31 ± 0,5 | 0,9953 | |||
| 32 ± 0,5 | 0,9954 | 0,9959 | 0,9964 | 0,9950 |
| 33 ± 0,5 | 0,9947 | |||
| 34 ± 0,5 | 0,9944 | |||
| 35 ± 0,5 | 0,9940 | |||
| 36 ± 0,5 | 0,9937 | |||
| 37 ± 0,5 | 0,9933 | |||
| 38 ± 0,5 | 0,9930 | |||
| 39 ± 0,5 | 0,9926 | |||
| 40 ± 0,5 | 0,9922 |
<br|> Um die Güte der eigenen Messwerte einzuschätzen, eignet sich ein Plotten der Messwerte mit den Referenzwerten aus der Literatur. Dies ermöglicht eine sehr einfache, optische Bewertung. Die folgende Abbildung zeigt das entsprechende Diagramm.
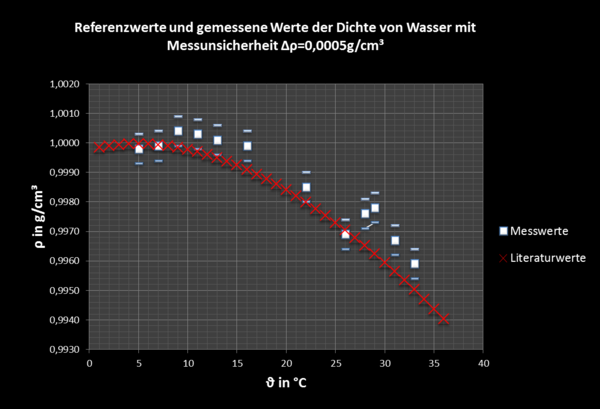
In Abbildung 6 ist deutlich zu erkennen, dass über die Hälfte der Messwerte auch unter Berücksichtigung der Messunsicherheiten für Dichte und Temperatur mehr als zufällig von den Literaturwerten abweichen. Diese Messwertintervalle beinhalten nicht den Literaturwert bei der entsprechenden Temperatur. Die gemessenen Werte sind tendenziell zu hoch. Es ist anzunehmen, dass bei den aufgenommenen Messwerten ein systematischer Fehler vorliegt. Da die Kalibrierung der Messapparatur wie beschrieben vorgenommen wurde, wird eine fehlerhafte Justierung der Waage beziehungsweise des Drahtes mit Senkkörper angenommen. Die Beobachtung, dass die Spitze des Hebelarmes bereits beim Aufbau etwas unter der Spitze des Stativfußes stand (siehe 3.3 Beobachtung/ Ergebnisse) weist darauf hin. Bei Aufnahme einer weiteren Messreihe sollte vor dem Eintauchen des Senkkörpers in die Flüssigkeit die Waage durch Aufhängen von Wägestücken ins Gleichgewicht gebracht werden. Der entsprechende Wert muss dann von allen aufgenommenen Messwerten abgezogen werden.
<br|>
Literatur
- Götz, Dahncke, Langensiepen. Handbuch des Physik-Unterrichts Sekundarbereich I. Band 1 (1990) + Band 2 (2000), Mechanik 1+2. Aulis Verlag Deubner & Co KG Köln.
- Heinicke, Glomski, Priemer, Rieß: Aus Fehlern wird man klug. Über die Relevanz eines adäquaten Verständnisses von „Messfehlern" in PdN-PhiS 5/59, Jg. 2010, S. 26-33.
- Kircher, Girwidz, Häußler: Physikdidaktik. Theorie und Praxis (2.Aufl. 2009). Springer-Verlag Berlin Heidelberg.
- Millar, R., & Osborne, J. F. (Eds.). (1998). Beyond 2000: Science Education for the Future. King’s College London.
- Hellwig, J. (2012). Messunsicherheiten verstehen: Entwicklung eines normativen Sachstrukturmodells am Beispiel des Unterrichtsfaches Physik (S. 5-12). Ruhr-Universität Bochum.
- Senatsverwaltung für Bildung, Jugend und Sport: Rahmenlehrplan für die Sekundarstufe I - Physik (1.Aufl. 2006).
- Senatsverwaltung für Bildung, Jugend und Sport: Rahmenlehrplan für die gymnasiale Oberstufe - Physik (1. Aufl. 2006).





