Wechselstromgenerator
| Wechselstromgenerator | |
 Wechselstromgenerator zur Überprüfung des Faradayschen Induktionsgesetzes | |
| Kurzbeschreibung | |
|---|---|
| Es soll anhand eines Wechselstromgenerators überprüft werden ob sich das Faradaysche Induktionsgesetz in 3 verschiedenen Teilexperimenten mit quantitativer Auswertung bewährt. | |
| Kategorien | |
| Elektrizitätslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung, Energie |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | schwer |
| Informationen | |
| Name: | Benjamin Busse |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Tobias Ludwig |
Die in diesem Beitrag vorgestellten Experimente mit einem Wechselstromgenerator dienen zur quantitativen Überprüfung des Faradayschen Induktionsgesetzes. Das Faradaysche Induktionsgesetz spiegelt wesentliche Zusammenhänge zwischen Elektrizitätslehre und Magnetismus wider und ist eine kompakte, jedoch nicht ganz erschöpfende Beschreibungsform für alle bekannten Induktionsphänomene. Der Wechselstromgenerator ist ein "Klassiker" unter den Anwendungsmöglichkeiten der elektromagnetischen Induktion. Der erste Wechselstromgenerator wurde 1832 von dem Franzosen Hippolyte Pixii konstruiert, kurz nachdem die elektromagnetische Induktion im Jahre 1831 von Michael Faraday im Experiment entdeckt wurde. Der erste praktisch anwendbare Generator wurde 1866 von Werner Siemens entwickelt (siehe [1] LEIFI Physik). Die induzierte Spannung beim Wechselstromgenerator ergibt sich aus dem Faradayschen Induktionsgesetz und lautet:
Streng genommen ist dies aber nur eine Näherung, da die Formel nur exakt gilt für ein vollkommen homogenes Magnetfeld im Inneren des Generators, was in der Realität nicht der Fall ist. Unter diesem Vorbehalt muss diese Formel bzw. diese Formel in leicht veränderter Form in dem kompletten Beitrag betrachtet werden.
In diesem Beitrag werden 3 Teilexperimente vorgestellt, in denen folgende, quantitative Abhängigkeiten überprüft werden:
1. Die induzierte Effektivspannung in Abhängigkeit der Winkelgeschwindigkeit der Induktionsspule.
2. Die Frequenz der Wechselspannung in Abhängigkeit der Winkelgeschwindigkeit der Induktionsspule.
3. Die induzierte Effektivspannung in Abhängigkeit der Stromstärke der Elektromagneten.
Inhaltsverzeichnis
Didaktischer Teil
In diesem didaktischen Teil soll es um einen speziellen Aspekt der Vermittlung physikalischen Wissens in der Schule gehen. Dieser spezielle Aspekt ist die Methodik mit der physikalisches Wissen in der Realität gewonnen wird. Man unterscheidet generell zwischen zwei sehr grundlegenden Methoden zur Gewinnung neuen physikalischen Wissens. Zum einen gibt es die hypothetisch-deduktive Methode und zum anderen die induktive Methode. Der Philosoph Sir Karl Popper hat wichtige Beiträge zu dieser Thematik erarbeit. Er beschreibt die induktive Methode bzw. induktive Schlussweise folgendermaßen: "Als induktiven Schluss oder Induktionsschluss pflegt man einen Schluss von besonderen Sätzen, die z.B. Beobachtungen, Experimente usw. beschreiben, auf allgemeine Sätze, auf Hypothesen oder Theorien zu bezeichnen." (Popper[1] 1976, S.1) Im Gegensatz zur induktiven Methode, bei der man vom Speziellen auf das Allgemeine schließt, geht die hypothetisch-deduktive Methode in der anderen Richtung vor, in dem sie vom Allgemeinen auf das Spezielle schließt. Konkret bedeutet dies, dass am Anfang des Erkenntnisprozesses die Theoriebildung bzw. Bildung einer allgemeinen Hypothese steht, als nächstes daraus spezielle Sätze abgeleitet werden und schließlich diese im Experiment oder in der Beobachtung überprüft werden.
Die Frage, welche der beiden vorgestellten Methoden in der Physik generell bevorzugt wird, lässt sich nicht eindeutig beantworten. Dies liegt daran, dass es Fälle des physikalischen Erkenntnisprozesses gibt, bei denen klarerweise die induktive Methode im Vordergrund steht und andere Fälle, in denen die hypothetisch-deduktive Methode bevorzugt wird. Ein Beispiel für die induktive Vorgehensweise ist die Ausarbeitung des in diesem Beitrag behandelten Induktionsgesetzes von Michael Faraday. Dieser fand 1831 beim Experimentieren des Zusammenhangs zwischen elektrischen Strömen und Magnetismus eher unvorhergesehen heraus, dass elektrische Ströme durch zeitliche Änderung von Magnetfeldern erzeugt werden können. Mit Hilfe weiterer Experimente gelang es Faraday kurze Zeit später das nach ihm benannte Gesetz zu formulieren ( vgl. Williams[2] 1965, S. 182–183, S. 191–195). Ein Beispiel für die hypothetisch-deduktive Methode ist Einsteins allgemeine Relativitätstheorie und die daraus abgeleitete Vorhersage und experimentelle Überprüfung der gravitativen Ablenkung von Lichtstrahlen durch große Massen. Die allgemeine Theoriebildung und deren erstmalige Veröffentlichung 1915 ging hier der speziellen, experimentellen Prüfung der Ablenkung von Licht durch die Sonne 1919 voran (vgl. Coles[3] 2000, S.1).
Was bedeuted das Ganze nun für die Vermittlung der physikalischen Inhalte im Schulunterricht? In welcher Reihenfolge sollten die Inhalte vermittelt werden? Zuerst die Experimente und dann das zugehörige, allgemeine Gesetz oder umgekehrt?
Die letzte Frage lässt sich sicherlich nicht einfach pauschal beantworten. Dies liegt daran, wie im letzten Abschnitt erläutert, dass die Methodik in der realen Erkenntnisgewinnung auch nicht eindeutig ist und wenn man die historische Erkenntnisgewinnung im Physikunterricht möglichst unverfälscht wiedergeben möchte, kommt es eben auf die spezielle Gesetzmäßigkeit an, ob die induktive oder deduktive Methode bevorzugt werden sollte. Hinzu kommt, dass es durchaus didaktische Gründe dafür gibt, von der historischen Erkenntnisgewinnung abzuweichen. Beispielsweise ist es sinnvoll neue Gesetzmäßigkeiten, die auf keinerlei Vorwissen der Schüler beruhen und insbesondere auch nicht aus noch allgemeineren Gesetzmäßigkeiten, die den Schülern bekannt sind, hergeleitet werden können durch die induktive Methode einzuführen, obwohl historisch die hypothetisch-deduktive Methode angewendet wurde. Wenn man dies nämlich nicht tut und der historischen Erkenntnisgewinnung folgt, dann entsteht bei den Schülern völlig zurecht der Verdacht, dass das Gesetz aus heiterem Himmel entstanden ist. Dies sollte vermieden werden. Wenn man dagegen in solchen Fällen die induktive Methode anwendet, dann nehmen die Schüler aktiv an der Gesetzesbildung teil oder zumindest wird ihnen dann die Entstehung des allgemeinen Gesetzes deutlich klarer, da es eben aus den konkreten Experimenten im Unterricht induktiv hervorgeht. Zu beachten bei der induktiven Methode im Unterricht ist aber generell, dass diese Methode ihre grundsätzlichen Schwächen hat. Aus einzelnen Experimenten kann nämlich vom logischen Standpunkt her niemals die Wahrheit des allgemeinen Gesetzes gezeigt werden (siehe Popper[1] 1976, S.1), erst recht nicht durch die sehr wenigen Messungen unter bestimmten Bedingungen im Unterricht. Es kann lediglich gezeigt werden, dass sich das allgemeine Gesetz zur Beschreibung der experimentellen Ergebnisse bewährt. Darauf muss unbedingt hingewiesen werden, sonst entsteht bei den Schülern eine naive Vorstellung der Erkenntnisgewinnung. In anderen Fällen kann die hypothetisch-deduktive Methode im Unterricht entgegen der historisch angewendeten Methode auch aus didaktischen Gründen sinnvoller sein. Dies ist der Fall, wenn das zu vermittelnde Gesetz nachvollziehbar aus noch allgemeineren Gesetzen, die den Schülern bekannt sind, hergeleitet werden kann. Dann entsteht bei den Schülern eben nicht der Eindruck, dass das Gesetz aus heiterem Himmel enstand, sondern folgt notwendig aus schon bekannten Gesetzen. Anschließend kann in speziellen, abgeleiteten Experimenten überprüft werden ob sich das zu vermittelnde Gesetz bewährt.
Versuchsanleitung
Aufbau
Für die in diesem Beitrag vorgestellten Experimente sind folgende Materialien von Nöten:
- 4 Spulen
- Stator mit 2 halbringförmigen Eisenkernen
- Rotor
- Motor mit regulierbarer Drehzahl
- Antriebsriemen
- Stangen und Muffen
- Drehzahlmessgerät mit Laser
- digitales Multi-/Voltmeter
- digitales Multi-/Amperemeter
- Multimeter mit der Möglichkeit zur Frequenzmessung
- Drehspulmessinstrument mit Messscheibe (Bereich: 0-10 V)
- Netzgerät
- Oszilloskop
- Scherentisch
- mindestens 5 Tischklemmen
- Schutzwand aus Plexiglas o.Ä.
- Stromkabel
Für den 1. Teilversuch werden zunächst die 2 Spulen, die als Elektromagneten dienen sollen, in den dafür vorgesehenen Stellen des Stators eingesetzt. Um ein möglichst homogenes Magnetfeld zwischen den beiden Spulen im inneren des Stators herstellen zu können, sollten die beiden Spulen möglichst die gleiche Windungszahl aufweisen. Die Windungszahl der Elektromagneten betrug in den hier vorgestellten Experimenten N=1200. Nachdem die 2 Spulen eingesetzt wurden, sollten sie mit dem Netzgerät mit Hilfe der Stromkabel verbunden werden, wobei die Stromkabel in den Eingang für Gleichstrom eingesetzt werden müssen. Zudem muss auf die richtige Polung geachtet werden, ansonsten heben sich die Magnetfelder der beiden Elektromagneten im Inneren der Spule auf. Als nächstes sollte die 3. und 4. Spule an den dafür vorgesehenen Stellen des Rotors im Inneren des Stators eingesetzt werden. Da diese beiden Spulen in Reihe geschaltet werden, können sie als eine Induktionsspule betrachtet werden. Anschließend sollte der Motor so aufgebaut werden, dass sich die Motorwelle sowohl horizontal als auch vertikal auf einer Höhe mit dem Rotor befindet. Eventuell ist dafür ein Scherentisch zur Höhenverstellung des Motors von Nöten. Danach sollte der Antriebsriemen so eingesetzt werden, dass er die Motorwelle und den Rotor miteinander verbindet. Der Stator in dessen Innerem sich der Rotor befindet, ist so auf dem Experimentiertisch zu verschieben, dass der Antriebsriemen gespannt ist und nicht locker herunterhängt. Wenn die richtige Position gefunden wurde, sollte der Stator möglichst noch mit zwei Tischklemmen am Experimentiertisch befestigt werden. Der Motor sollte auch über eine Stangenkonstruktion mit einer Tischklemme am Experimentiertisch befestigt werden. Ansonsten werden nämlich bei der Rotation des Rotors samt Induktionsspule und der Motorwelle während der Versuche der ganze Stator und Motor in leichte Bewegungen versetzt und auf dem Experimentiertisch verrückt. Um die Drehzahl des Rotors akkurat messen zu können, muss auf diesen noch ein ca. 2 cm breiter, schwarzer Streifen Klebeband geklebt werden. Darauf wiederum muss ein ca. 1 cm breiter und langer Streifen aus reflektierendem Material angebracht werden, welches sich normalerweise im Zubehör des Drehzahlmessgeräts befindet. Dieses spezielle Material dient dazu, das Laserlicht des Drehzahlmessgeräts zu reflektieren und somit eine Zählung der Umdrehungen zu ermöglichen. Für das Drehzahlmessgerät muss zusätzlich mit Hilfe einer Tischklemme, Stangen, Muffen und einer Klemme eine Halterung gebaut werden, sodass das Laserlicht des Messgerätes mittig auf den schwarzen Klebestreifen am Rotor ausgerichtet ist. Danach muss noch die Induktionsspule über Stromkabel mit dem digitalen Multi-/Voltmeter verbunden werden. Parallel dazu sollte zu Demonstrationszwecken der induzierten Spannung noch ein analoges Drehspulmessinstrument geschaltet werden. Zuletzt ist noch ganz wichtig eine durchsichtige Schutzwand z.B. aus Plexiglas vor dem Generator zu errichten, da nicht garantiert werden kann, dass bei den recht hohen Drehzahlen der Induktionsspule kleinere Teile abgelöst werden und mit hoher Geschwindigkeit unkontrolliert durch den Raum fliegen. Die Schutzwand sollte auch mit einer Tischklemme am Experimentiertisch befestigt werden. Dieses gewisse Sicherheitsrisiko ist auch der Hauptgrund, warum die Versuche mit dem Generator nur als Demonstrationsversuche vom Lehrer durchgeführt werden sollten und alle Schüler sich dabei möglichst in Sicherheit hinter der Schutzwand befinden sollten. Alle Messgeräte und die Steuereinheit des Motors sollten sich möglichst auch hinter der Schutzwand befinden oder im Falle der Messgeräte zumindest gut sichtbar sein, wenn man hinter der Schutzwand steht.
Für den 2. Teilversuch wird ein Multimeter benötigt, welches Frequenzen von Wechselströmen messen kann und an die Induktionsspule anzuschließen ist. Wenn dies nicht vorhanden ist, kann alternativ auch ein Oszilloskop verwendet werden, welches zu Demonstrationszwecken der Schwingungskurven ohnehin an die Induktionsspule angeschlossen werden sollte. In diesem Fall muss die Frequenz des Schwingungsvorgangs mit Hilfe der jeweils abgelesenen Periodendauer am Oszilloskop berechnet werden. Es bietet sich zudem an, den 1. und 2. Teilversuch zusammen durchzuführen, da beide Versuche Abhängigkeiten von der Winkelgeschwindigkeit bzw. der Drehzahl der Induktionsspule überprüfen.
Für den 3. Teilversuch wird sowohl das Drehzahlmessgerät als auch das Oszilloskop nicht mehr benötigt. Für diesen Teilversuch muss lediglich die Stromstärke am Drehregler des ohnehin vorhandenen Netzgerätes variiert und mit einem zusätzlichen digitalen Multi-/Amperemeter gemessen werden. Dazu muss das Multi-/Amperemeter in Reihe geschaltet werden mit einem Stromkreis bestehend aus Netzgerät und Elektromagnet (Spule). Dabei kann einer der beiden Stromkreise, je ein Stromkreis pro Elektromagnet, beliebig gewählt werden. Anschließend muss jeweils die Effektivspannung wie beim 1. Teilversuch mit einem Multi-/Voltmeter gemessen werden.
Durchführung
Für den 1. Teilversuch werden zunächst alle benötigten, elektronischen Geräte eingeschaltet, also das Netzgerät, der Motor, das Drehspulmessinstrument, das digitale Multi-/Voltmeter und das Drehzahlmessgerät. Es ist darauf zu achten, dass sich die Steuereinheit des Motors beim Einschalten im Leerlauf oder auf dem niedrigsten Drehzahllevel befindet. Die Spannungs- und Stromwerte des Netzgerätes können relativ beliebig eingestellt werden, jedoch sollte nicht das rote Lämpchen am Netzgerät aufleuchten. Gute Messergebnisse werden z.B. mit den Einstellungen 10 Volt und 1,2 Ampere erzielt. Nun kann das Drehzahllevel mit Hilfe der Steuereinheit langsam angehoben werden und bei einem beliebigen, nicht zu großen Wert wieder gestoppt werden. In diesem Zustand wird nun die Drehzahl und die induzierte Spannung an den entsprechenden Messgeräten abgelesen. Da die Messwerte aufgrund der Rotationsbewegung und kleineren Ungleichmäßigkeiten wahrscheinlich relativ viel schwanken werden zeitlich, sollten jeweils mindestens 6 Messwerte pro Einstellung aufgenommen werden, damit die Mittelwert- und Vertrauensbereichbildung angewendet werden kann ( vgl. Müller[4] 2007, S. 29-30). Für die Messung der Effektivspannung kann auch alternativ jeweils einmalig der Wert am etwas ungenaueren Drehspulmessinstrument abgelesen werden, da der Zeiger des Geräts in der Regel nur geringfügig schwankt. Im Folgenden wird im Versuch die Drehzahl weiter stückweise erhöht und die entsprechenden Messwerte abgelesen. Ca. 10 verschiedene Einstellungen der Drehzahl reichen aus um aussagekräftige Ergebnisse zu erzielen.
Der 2. Teilversuch kann parallel zum 1. Teilversuch durchgeführt werden. Hier muss lediglich das Oszilloskop mit eingeschaltet und passende Einstellungen vorgenommen werden(Skalierung der Spannungs- und Zeitachse etc.). Zudem muss nun das Multimeter mit der Möglichkeit zur Frequenzmessung einer Wechselspannung eingeschaltet werden, wenn man nicht die Frequenz über die Periodendauer, welche am Oszilloskop abgelesen werden kann, bestimmen möchte. Bei der Frequenzmessung mit einem Multimeter sollten aus den gleichen Gründen wie im 1. Teilversuch pro Einstellung mindestens 6 Messwerte aufgenommen werden. Man kann natürlich auch den 2. Teilversuch getrennt vom 1. Teilversuch durchführen.
Für den 3. Teilversuch muss das Multi-/Amperemeter, welches in Reihe geschaltet ist mit einem Stromkreis bestehend aus Netzgerät und Elektromagnet, eingeschaltet werden. Wie schon im 1. Teilversuch müssen ein Drehspulmessinstrument und ein Multi-/Voltmeter, welche parallel über die Induktionsspule geschaltet sind, eingeschaltet sein. Der Regler an der Steuereinheit des Motors ist auf eine beliebige Drehzahl einzustellen. Sie muss lediglich eine saubere Rotationsbewegung der Induktionsspule bewirken. Der Regler für die Stromstärke am Netzgerät muss zu Beginn des Versuches auf 0 Ampere eingestellt werden. Nun kann die Aufnahme der Messwerte beginnen, indem der Regler für Stromstärke leicht hochgedreht wird und anschließend die ersten Messwerte für die Stromstärke und Effektivspannung an den entsprechenden Geräten abgelesen werden. Die Werte für die Stromstärke werden kaum schwanken, da das Netzgerät konstante Werte liefert. Im Folgenden wird der Regler für die Stromstärke stückweise hochgedreht und die entsprechenden Messwerte abgelesen. Ca. 10 verschiedene Einstellungen der Stromstärke reichen für ein aussagekräftiges Ergebnis wieder aus.
Ergebnisse
Es wurden in den Teilexperimenten folgende Messergebnisse erzielt. Zu beachten ist, dass im Falle der Aufnahme von 6 Messwerten pro Einstellung einer bestimmten Messgröße (Drehzahl und Frequenz) der Übersicht halber nur die Mittelwerte in den Tabellen aufgenommen wurden.
| Drehzahl n [min-1] | Effektivspannung Ueff [V] | Frequenz ν [Hz] |
|---|---|---|
| 271 | 1,85 | 4,52 |
| 339 | 2,30 | 5,64 |
| 417 | 2,80 | 6,95 |
| 539 | 3,55 | 8,96 |
| 597 | 4,00 | 9,95 |
| 656 | 4,35 | 10,91 |
| 754 | 5,00 | 12,58 |
| 836 | 5,55 | 13,93 |
| 912 | 6,05 | 15,19 |
| 958 | 6,35 | 15,96 |
| Strom I [mA] | Effektivspannung Ueff [V] |
|---|---|
| 29 | 1,00 |
| 59 | 1,50 |
| 105 | 1,90 |
| 145 | 2,50 |
| 197 | 3,00 |
| 243 | 3,50 |
| 292 | 4,00 |
| 348 | 4,50 |
| 411 | 4,95 |
Auswertung
Messunsicherheiten:
Im 1. Teilversuch wurden die physikalischen Größen Drehzahl n und Effektivspannung Ueff gemessen. Die Drehzahlen wurden mit dem digitalen Drehzahlmessgerät PeakTech 2780 gemessen. Laut Herstellerangaben beträgt die systematische Messabweichung dieses Gerätes: ±(0,05%+0,1min-1). Die zufällige Messabweichung ergab sich aus dem Vertrauensbereich der je 6 gemessenen Werte pro eingestellter Drehzahl (siehe Müller[4] 2007, S. 29-30). Die gesamte Messabweichung ergab sich nun aus der pythagoreischen Addition der systematischen und zufälligen Messabweichung (siehe Müller[4] 2007, S. 31). Hier ein kurzes Rechenbeispiel für die erste eingestellte Drehzahl:
Es wurden folgende 6 Messwerte aufgenommen (die 1. Nachkommastelle wurde aufgrund zu starker Schwankungen nicht mit aufgenommen):
| Messung | Drehzahl n [min-1] |
|---|---|
| 1. Messung | 272 |
| 2. Messung | 271 |
| 3. Messung | 271 |
| 4. Messung | 270 |
| 5. Messung | 270 |
| 6. Messung | 271 |
Der Mittelwert betrug n = 270,83 min-1 ≈ 271 min-1. Der Mittelwert wurde auf die letzte Stelle vor dem Komma gerundet, da eine genauere Angabe eine genauere Messung implizieren würde als es tatsächlich der Fall war. Die zufällige Messabweichung ergab sich aus dem Vetrauensbereich der Messreihe zu uz ≈ ±0,3 min-1. Die systematische Messabweichung ergab sich zu us = ±(0,0005·271+0,1) min-1 ≈ ±0,2 min-1. Die gesamte Messabweichung ergab sich nun zu u = ±(0,32+0,22)1/2 min-1 ≈ 0,4 min-1. In solch einem Fall wie diesem wurde die gesamte Messabweichung auf ±1 min-1 aufgerundet, da sonst das Ergebnis wieder eine zu genaue Messung implizieren würde bzw. im Falle einer Abrundung die gesamte Messabweichung komplett verschwinden würde. Da bei jeder Einstellung der Drehzahl die Werte in ähnlicher Weise in geringem Umfang schwankten, ergab sich letztendlich für jede Einstellung eine gesamte Messabweichung von ±1 min-1. Um den Messprozess etwas zu verkürzen, wurden für die Spannung die Effektivwerte am etwas ungenaueren Drehspulmessinstrument abgelesen. Der Zeiger des Messgerätes schwankte in geringem Ausmaß, sodass eine eindeutige Ablesung der Messwerte gewährleistet war. Die zufällige Messabweichung ergab sich hierbei aus einer halben Skaleneinteilung einer Messscheibe von 0-10 V zu: ±0,05 V. Eine Angabe über die systematische Messabweichung des Messgerätes war am Versuchsplatz nicht gegeben. Somit wurde die gesamte Messabweichung durch die zufällige Messabweichung abgeschätzt und betrug: u = ±0,05 V.
Für den 2. Teilversuch wurde neben der Drehzahl n aus dem 1. Teilversuch zusätzlich noch die Frequenz ν der induzierten Wechselspannung gemessen. Diese wurde mit dem digitalen Multimeter MetraHit 18s gemessen. Die systematische Messabweichung betrug laut Herstellerangaben: ±(0,1%+0,03Hz). Die zufällige Messabweichung der Frequenz ergab sich analog zur Drehzahlmessung aus dem Vertrauensbereich von je 6 Einzelmessungen pro Einstellung. Die gesamte Messabweichung ergab sich wiederum analog zur Drehzahlmessung aus der pythagoreischen Addition der systematischen und zufälligen Messabweichung. Sie betrug für die ersten 7 Einstellungen gerundet auf die 1. signifikante Stelle u= ±0,04 Hz und für die letzten 3 Einstellungen u= ±0,05 Hz.
Für den 3. Teilversuch wurde der Strom I gemessen, welcher durch einer der beiden Elektromagneten (Spulen) floss und wiederum die induzierte Effektivspannung Ueff. Die Effektivspannungen wurden wieder mit dem Drehspulmessgerät gemessen, wobei sich die gesamte Messabweichung analog zum 1. Teilversuch aus einer halben Skaleneinteilung zu u = ±0,05 V ergab. Die Ströme wurden wieder mit dem digitalen Multimeter MetraHit 18s gemessen. Laut Herstellerangaben betrug hier die systematische Messabweichung: ±(0,5%+0,001A). Die zufällige Messabweichung wurde mit einem Digit abgeschätzt und betrug uz = 0,001A. Da die Messwerte für die Gleichströme aufgrund der sehr konstanten Versorgung durch das Netzgerät kaum schwankten, waren hier mehrere Einzelmessungen pro Einstellung nicht von Nöten. Die gesamte Messabweichung ergab sich wiederum aus der pythagoreischen Addition der systematischen und zufälligen Messabweichung. Sie betrug für die ersten 6 Einstellungen gerundet auf die 1. signifikante Stelle u= ±0,002 A und für die letzten 3 Einstellungen u= ±0,003 A.
Berechnungen und graphische Auswertung
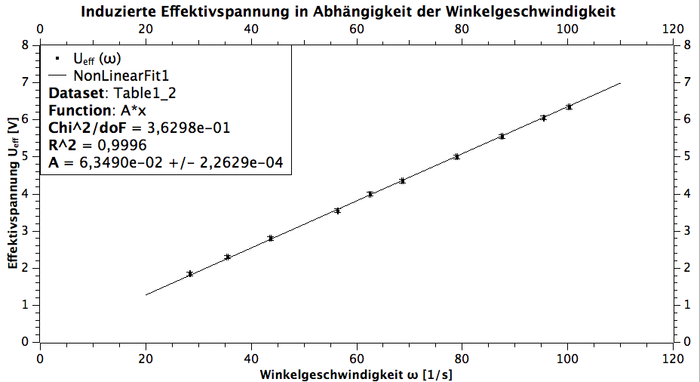
Wie im einleitenden Text dieses Beitrages angekündigt, sollte mit dem 1. Teilversuch die induzierte Effektivspannung Ueff in Abhängigkeit der Winkelgeschwindigkeit ω der rotierenden Induktionsspule untersucht werden. Gemessen wurde in dem Versuch aber nicht die Winkelgeschwindigkeit, sondern die Drehzahl n. Der Drehzahl entspricht von den Einheiten her eine Frequenz ν, sodass zur Umrechnung die Messwerte mit ihren Unsicherheiten lediglich mit dem Faktor 2π multipliziert werden mussten, da der Zusammenhang ω = 2πν gilt. Zudem mussten die Messwerte mit ihren Unsicherheiten noch durch den Faktor 60 dividiert werden, da die Drehzahlen in min-1 gemessen wurden und nicht in s-1. Nachdem diese Umrechnungen durchgeführt wurden, konnte nun die Abhängigkeit der Effektivspannung von der Winkelgeschwindigkeit graphisch ausgewertet werden. Nach dem Faradayschen Induktionsgesetz gilt :
Da nun Ueff proportional zu ω sein sollte nach der Theorie, wurde für den Graphen eine Fitfunktion f(x)=A·x erstellt:
Wie man am Graphen erkennen kann, wurde die Proportionalität zwischen der Effektivspannung und der Winkelgeschwindigkeit sehr gut bestätigt, was man auch an dem Bestimmtheitsmaß R2 erkennen kann, welches sehr nahe bei 1 liegt. Zudem wurden die Messunsicherheiten gut abgeschätzt, wobei sie tendenziell noch etwas zu groß ausgefallen sind, was man an dem χ2/doF erkennen kann, welches kleiner als 1 ist. Abschließend lässt sich zum 1. Teilversuch sagen, dass sich das Faradaysche Indukuktionsgesetz hier experimentell bewährt hat, wobei dies zu überprüfen das Ziel dieses Versuches war.
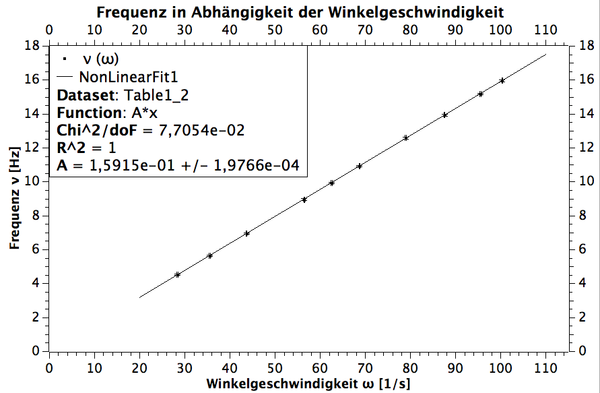
Mit dem 2. Teilversuch sollte die Frequenz ν der induzierten Wechselspannung in Abhängigkeit der Winkelgeschwindigkeit ω der rotierenden Induktionsspule untersucht werden. Es gelten hier die gleichen Umrechnungen beim Übergang von der gemessenen Drehzahl n zur Winkelgeschwindigkeit ω wie im 1. Teilversuch. Nach dem Faradayschen Induktionsgesetz gilt für die induzierte Wechselspannung:
Aus der Formel lässt sich ablesen, dass die Frequenz ν der Sinus-förmigen Wechselspannung proportional zur Winkelgeschwindigkeit ω sein muss. Wobei im Allgemeinen der Zusammenhang ν = ω/(2π) ≈ 0,15915ω gilt. Aus diesem Grund wurde für den Graphen ν(ω) wieder eine Fitfunktion f(x)=A·x erstellt, wobei diesmal der Steigungsfaktor A exakt vorauszusehen war und A = ≈ 0,15915 betragen müsste:
Wie man wieder am Graphen erkennen kann, wurde die Proportionalität zwischen der Frequenz der Wechselspannung und der Winkelgeschwindigkeit der Induktionsspule sehr gut bestätigt, was man auch wieder an dem Bestimmtheitsmaß R2 erkennen kann, welches bei 1 liegt. Zudem stimmt der Steigungsfaktor A in den ersten 5 signifikanten Stellen exakt mit dem theoretischen Wert überein. Die Messunsicherheiten wurden wieder etwas zu groß abgeschätzt, da das χ2/doF wieder kleiner als 1 ist. Abschließend lässt sich auch im 2. Teilversuch festhalten, dass sich das Faradaysche Indukuktionsgesetz hier experimentell bewährt hat, wobei dies zu überprüfen wiederum das Ziel dieses Versuches war.
Bei dem 3. Teilversuch wurde die Abhängigkeit der induzierten Effektivspannung Ueff von der Stromstärke I, die durch die beiden Elektromagneten (Spulen) floss, untersucht. Diese Abhängigkeit tritt im Faradayschen Induktionsgesetz nur implizit zu Tage, in dem Sinne, dass im Falle der Elektromagneten ihre Magnetfeldstärke B von der Stromstärke I abhängt. Das Magnetfeld im inneren des Generators zwischen den Elektromagneten kann im Allgemeinen nicht als konstant angesehen werden. Nur im Falle von Helmholtzspulenpaaren, deren Abstand genau dem Radius der Spulen entspricht, kann in sehr guter Näherung das Feld auf der Spulenachse zwischen den Spulen als konstant betrachtet werden. In den realen Experimenten dieses Beitrages war dies nicht gegeben, wie man auch in dem Bild am Anfang dieses Beitrages erkennen kann. Der Abstand der beiden Spulen war deutlich größer als ihr Radius, wobei man dazu sagen muss, dass zusätzlich noch 2 ringförmige Eisenkerne mit den Spulen verbunden waren. Ob das Magnetfeld im Inneren nun wirklich homogen ist oder nicht, spielt letztendlich für die proportionale Abhängigkeit der induzierten Effektivspannung vom Strom durch die Elektromagneten keine Rolle. Dies zeigt folgende Überlegung: Die Magnetfeldstärke der stromdurchflossenen Elektromagneten an beliebigen Raumpunkten ergibt sich aus dem Biot-Savart-Gesetz. Dieses lautet für zeitlich konstante Ströme allgemein:
Das Faradaysche Induktionsgesetz lautet in allgemeiner, integraler Form:
Aus den letzten beiden Formeln unter Berücksichtigung, dass das Superpositionsprinzip für Magnetfelder gilt, dass im Experiment 2 Elektromagneten vorhanden waren und der Annahme, dass durch sie der selbe Strom I floss, folgt:
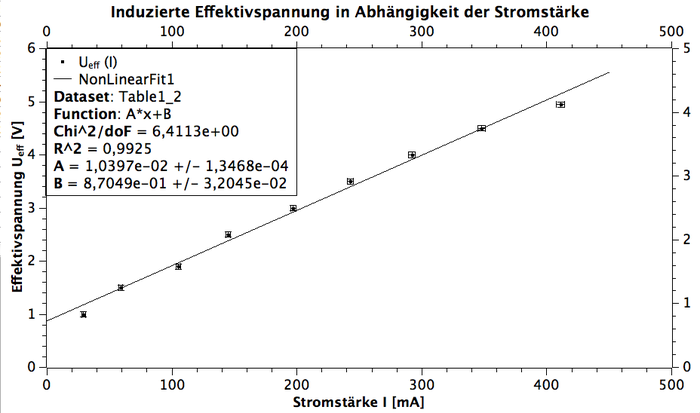
Wenn die induzierte Spannung Uind, wie gerade gezeigt, proportional zur Stromstärke I ist, dann wird auch ihr Maximal- und Effektivwert proportional zu I sein. Dies gilt aber nur unter dem Vorbehalt, dass im Inneren des Generators keine anderen magnetischen Feldstärken vorhanden sind als die, die unmittelbar durch die Elektromagneten erzeugt werden. In den Experimenten, die diesem Beitrag zu Grunde liegen, waren jedoch noch zusätzlich zwei Eisenkerne mit den Spulen verbunden. Diese Eisenkerne sind ferromagnetisch und demzufolge ist ein Hystereseverhalten bei ihnen zu erwarten. Dies bedeutet, dass sie die Eigenschaft besitzen selbst ein gerichtetes, magnetisches Feld zu erzeugen, wenn sie unter dem Einfluss eines äußeren Magnetfeldes stehen. Dieses äußere Magnetfeld wird in diesem Experiment durch die beiden Spulen erzeugt. Hinzu kommt, dass eine Restmagnetisierung, auch "Remanenz" genannt, der Eisenkerne auch dann bestehen bleibt, wenn die äußere Magnetfeldstärke wieder auf Null zurückgefahren wird (vgl. Demtröder[5] 2013, S. 111). Daraus folgt für das hier behandelte Experiment, dass auch in dem Fall, dass kein Strom durch die Spulen fließt, immer noch eine Spannung induziert wird, solange die Induktionsspule rotiert. Vorausgesetzt natürlich, dass vorher schonmal Strom durch die Spulen floss und infolgedessen die Eisenkerne magnetisiert wurden. Somit kann davon ausgegangen werden, dass sich bei der Auswertung der Messungen keine Proportionalität zwischen Stromstärke und induzierter Effektivspannung erkennen lässt. Vielmehr sollte es eine Überlagerung zwischen einer Ursprungsgerade, welche durch die Spulen erzeugt wird, und einer Hysteresekurve, welche durch die Eisenkerne erzeugt wird, geben. Insbesondere sollte im Falle einer linearen Fit-Funktion als Näherung für diese Überlagerung, der Y-Achsenabschnitt einen positiven Wert besitzen. Die zugehörige Gerade sollte sich also deutlich von einer Ursprungsgerade abheben. Folgender Graph resultierte aus den Messungen, die diesem Beitrag zugrunde lagen:
Wie erwartet, kann man deutlich erkennen, dass sich die Gerade von einer Ursprungsgerade abhebt. Der Y-Achsenabschnitt liegt bei Ueff ≈ 0,87 V. Das Bestimmtheitsmaß R2 = 0.9925 liegt nahe bei Eins, was für eine gute Näherung spricht. Trotzdem sind die Abweichungen zu groß, um sagen zu können, dass hier wirklich ein linearer Zusammenhang vorlag. Das χ2/doF ist nämlich deutlich größer als Eins. Zudem lässt sich die Tendenz erkennen, wenn man nur die einzelnen Punkte im Graphen betrachtet, dass die Steigung mit größerer Stromstärke I geringer wird. Dies deutet auch auf den Hystereseeffekt hin, da die Hysteresekurve im Allgemeinen mit steigendem I bzw. B schwächer steigt und sich an einen konstanten Maximalwert anschmiegt (siehe Demtröder[5] 2013, S. 111). Die letzten Aussagen bleiben jedoch etwas spekulativ und zudem kann mit dem vorliegenden Graphen das Faradaysche Induktionsgesetz nicht direkt bestätigt werden. Um die ganze Sache einfacher und klarer zu gestalten, sollte man den Versuch ein wenig modifizieren und anstelle der kleinen Spulen mit Eisenkernen, ein großes Helmholtzspulenpaar verwenden. Dieses müsste idealerweise groß genug sein, dass sich die Induktionsspule bei der Rotationsbewegung immer im annähernd homogenen Magneteldbereich zwischen den Spulen befindet. Da im Falle des Helmholtzspulenpaares keine Eisenkerne benötigt werden, ist hier auch kein Hystereseeffekt zu erwarten und somit müsste ein proportionaler Zusammenhang zwischen I und Ueff messbar sein.
Sicherheitshinweise
Wie schon im Aufbau beschrieben, ist generell bei Versuchen mit einem motorbetriebenen Generator ganz wichtig eine durchsichtige Schutzwand z.B. aus Plexiglas zwischen Experimentator und Generator zu errichten, da nicht garantiert werden kann, dass bei den recht hohen Drehzahlen der Induktionsspule kleinere Teile abgelöst werden und mit hoher Geschwindigkeit unkontrolliert durch den Raum fliegen. Dieses gewisse Sicherheitsrisiko ist wie schon erwähnt der Hauptgrund, warum die Versuche mit dem Generator nur als Demonstrationsversuche vom Lehrer durchgeführt werden sollten und alle Schüler sich dabei möglichst in Sicherheit hinter der Schutzwand befinden sollten.
Literatur
- ↑ 1,0 1,1 Popper, K.R. (1976): Logik der Forschung; J.C.B. Mohr, Tübingen
- ↑ Williams, L.P. (1965): Michael Faraday: a biography; Chapman and Hall, London
- ↑ Coles, P. (2000): Einstein, Eddington and the 1919 Eclipse; Proceedings of International School on „The Historical Development of Modern Cosmology“, Valencia
- ↑ 4,0 4,1 4,2 Müller, U. (2007): Physikalisches Grundpraktikum. Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik; Berlin
- ↑ 5,0 5,1 Demtröder, W. (2013): Experimentalphysik 2 - Elektrizität und Optik; Springer-Verlag, Berlin Heidelberg
Siehe auch
LEIFI Physik: Elektromagnetische Induktion; http://www.leifiphysik.de/themenbereiche/elektromagnetische-induktion/geschichte [10.03.2016]