Wärmestrahlung eines schwarzen Körpers
| Wärmestrahlung eines schwarzen Körpers | |
 Bildunterschrift des Experiments | |
| Kurzbeschreibung | |
|---|---|
| Experimetelle Herleitung des Stefan-Boltzmann-Gesetzes über die Strahlung eines schwarzen Körpersals als Beispiel für die mathematische Modellierung eines physikalischen Prozesses. | |
| Kategorien | |
| Thermodynamik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Gunter Strüven |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Die Empfindung von Wärme auf der Haut, wenn man eine heiße Oberfläche vor sich hat, so z. B. bei einem Ofen oder der Glut eines Lagerfeuers, ist den meisten Menschen aus dem Alltag vertraut, ebenso die Beobachtung, dass das Wärmegefühl um so intensiver ist, je heißer diese Oberfläche ist. Mit dem hier beschriebenen Versuch kann die quantitative Abhängigkeit der Emission von Wärmestrahlung von der Oberflächentemperatur eines Körpers aufgezeigt werden.
Um auszuschließen, dass neben der Temperatur auch andere Oberflächeneigenschaften die Messung beeinflussen, wird ein Körper eingesetzt, der Wärmestrahlung möglichst vollständig absorbiert und dessen Emission von Wärmestrahlung möglichst wenig von Material und Eigenschaften der Oberfläche abhängig sind, der also einem sog. idealen 'schwarzen Körper' möglichst nahe kommt.
Die Auswertung der mit dem Versuch erzielbaren Messergebnisse führt zum Stefan-Boltzmann-Gesetz über die Strahlung eines schwarzen Körpers.
Der Versuch ist gut geeignet, Schülerinnen und Schülern (SuS) eine grundlegende Methode der Physik wie auch anderer Naturwissenschaften zu vermitteln: die mathematische Modellierung von physikalischen Vorgängen, also ihre Beschreibung durch Formeln, die auf Messwerten beruhen, die also in einem physikalischen Versuch und damit unter idealisierten Bedingungen gewonnen werden.
Inhaltsverzeichnis
Didaktischer Teil
Für den erfolgreichen Einsatz dieses Experimentes im Unterricht benötigen die SuS Vorkenntnisse: Auch in der SEK II werden viele SuS nicht sicher zwischen den drei Wärmeübertragungsvorgängen Wärmestrahlung, Wärmeleitung und Konvektion differenzieren können. Dieses Wissen ist ggf. aufzufrischen. Im Physikunterricht der SEK II wird Wärmestrahlung unter dem Begriff Infrarotstrahlung als Teil des Spektrums der EM-Wellen eingeordnet. Damit kann auch vorausgesetzt oder ggf. vorab vermittelt werden, dass die Ausbreitung von Infrarotstrahlung analog zu der von sichtbarem Licht erfolgt (geometrische Optik). In Vorbereitung dieses Versuchs sollte den SuS außerdem das Konzept des „idealen schwarzen Körpers“ vermittelt werden, der ungestört durch Oberflächeneigenschaften auftreffende EM-(Infrarot- wie sichtbare) Strahlung vollständig absorbiert und dessen Emission dieser Strahlung nur temperaturabhängig ist, also ebenfalls nicht durch Oberflächeneigenschaften beeinflusst wird.
Experimentieren und Modellbildung sind wichtige Anforderungen im Kompetenzbereich Erkenntnisgewinnung/ Methoden der Physik (vgl. Senatsverwaltung für Bildung, Jugend und Sport, [1] (2006), S.10, sowie Priemer [2] (2012). Hierzu gehören sowohl gegenständliche Modelle, hier als Abbild der Realität (vgl. Kircher [3] , Kap. 23, Modellbegriff und Modellbildung in der Physikdidaktik, S. 272-273), wie auch theoretische Modelle (hier Formeln, also symbolische Modelle, vgl. Priemer [4] (2012)), die eine mathematische Modellierung des beobachteten Phänomens dartellen.
- Aus einem von vielen Menschen im Alltag wahrgenommenen Phänomen (ein Ofen oder Feuer erwärmt die Umgebung, dabei kommen alle drei Wärmeübertragungsmechanismen zum Tragen) wird ein Aspekt (die auf der Haut wahrnehmbare Wärmestrahlung) isoliert betrachtet. Dafür wird ein Versuch konzipiert, bei dem durch Messungen das interessierende Phänomen (hier die Abgabe von Wärmestrahlung aufgrund der Tempertur eines Körpers bzw. einer Oberfläche) durch Messungen quantitativ erfasst wird, möglichst unter Ausschluss von anderen Einflüssen wie z. B. Farbe oder Struktur der Oberfläche, also mittels eines (angenäherten) schwarzen Körpers.
- Dieser quantitative Zusammenhang zwischen Oberflächentemperatur und Strahlungsintensität kann mathematisch beschrieben werden - damit wird ein mathematisches Modell dieses Zusammenhangs erarbeitet, das zur Beschreibung bzw. Prognose dieses Phänomens im Alltag dienen kann (z. B. bei der Auswahl eines Heizungssystems oder bei Klimamodellen). Das es sich um eine mathematische Modellierung handelt, wird hier besonders deutlich, da der funktionale Zusammenhang nicht wie meist im Schulunterricht ein (auch ohne mathematische Formulierung intuitiv leicht erfassbarer) linearer oder quadratischer ist sondern einer in der 4. Potenz.
- Eine grafische Aufbereitung und damit Visualisierung der Messwerte unterstützt das Erkennen eines mathematischen Zusammenhangs und damit die Modellbildung.
Zum Wesen dieser naturwissenschaftlichen Arbeitsweise gehört auch das Hinterfragen der Methoden, Ergebnisse und Modelle: Die gemeinsame grafische Darstellung von Messwerten und dem Ergebnis der mathematischen Modellierung kann anschließend zu einer Diskussion über die beobachtbaren Abweichungen der Messwerte vom Modell und damit über die Qualität des Versuchsaufbaus, über zufällige und systematische Messfehler und ggf. auch über das Prinzip der mathematischen Modellierung realer Phänomene genutzt werden. Es kann auch hinterfragt werden, inwiefern die für den Versuch gemachten Idealisierungen (hier: Oberflächen als ideale schwarze Körper) die Aussagekraft des Modells im Alltag einschränken.
Das Lernziel ist erreicht, wenn die SuS erkennen, dass diese naturwissenschaftliche Arbeitsweise ein geeignetes Mittel bzw. ein Werkzeug ist, um Phänomene in der Umwelt zu beschreiben und zu erklären, zwar nicht perfekt und nicht als absolute Wahrheit, aber ausreichend, um notwendige Prognosen z. B. bei der Planung einer Heizung oder bei Berechnungen für Klimaphänomene zu ermöglichen.
Eine durchdachte und gut strukturierte Vermittlung dieses Versuchs mit einem relativ abstrakten Beobachtungsgegenstand und mit nicht direkt, sondern nur messtechnisch wahrnehmbaren Vorgängen ist wesentlich für den Lernerfolg. Das bedeutet konkret:
Es ist den SuS zunächst ein gutes Verständnis von Aufbau und Funktion der einzelnen Komponenten des Versuchsaufbaus zu vermitteln. Dabei sollte man sich auf das beschränken, was für den Versuch relevant ist, und auf Einzelheiten hinsichtlich der inneren Funktionsweise verzichten, soweit diese für das Verständnis des Versuchs nicht erforderlich sind (und man nicht mit dem Anspruch kollidiert, auch bei Vereinfachungen physikalisch unkorrekte Beschreibungen zu vermeiden).
- Der Rohrofen mit dem Schwarzkörpereinsatz wird den SuS als reale Näherung eines idealen schwarzen Körpers erklärt, der in dem Versuch mit Hilfe der Heizung auf Temperaturen TR im Bereich von 300 K (Raumtemperatur) bis 700 K erwärmt wird und dessen Temperatur gemessen und fortlaufend protokolliert werden kann. Mit der Blende wird (analog zur Optik in der SEK I, s. auch Bild 1) ein Strahlungskegel mit dem Schwarzkörpereinsatz des Rohrofens als definierte Strahlungsquelle erzeugt und störende, d. h. undefinierte Infrarotstrahlung z. B. von der erwärmten Oberfläche des Ofens abgeschirmt.
- Auch die „Thermosäule nach Moll“ wird als reale Näherung eines idealen schwarzen Körpers erklärt, der sich im inneren des Metallkörpers befindet, wie dieser Raumtemperatur (T0) hat und der durch die trichterförmige metallisch blanke und polierte Öffnung die gesamte durch die Öffnung einfallende Strahlung aufnimmt (s. ebenfalls Bild 1).
Erst darauf aufbauend (und mit den Vorkenntnissen über schwarze Körper) lässt sich ein Verständnis von den Vorgängen während des Versuchs („was geschieht mit der Strahlung?“) erarbeiten: Es wird in der Idealisierung davon ausgegangen,
- dass beide Körper nur abhängig von ihrer eigenen Temperatur TR bzw T0 (also unabhängig z. B. von Oberflächeneigenschaften) Infrarotstrahlung emittieren,
- dass hiervon (abhängig von der Geometrie des Versuchsaufbaus, insbesondere Blendengröße, Öffnungsgröße der „Thermosäule nach Moll“, Abstände) ein bestimmter Teil auf den jeweils gegenüberliegenden schwarzen Köper trifft und dass jeder der beiden die auftreffende Strahlung des Gegenübers vollständig absorbiert,
- dass Absorption und Emission jeweils einen Energiefluss darstellen, der als (Strahlungs-)Leistung beschreibbar ist,
- dass bei der Thermosäule die Differenz zwischen der absorbierten und der emittierten Strahlungsleistung bei konstanter eigener (Raum-)Temperatur T0 nur von der Temperatur TR des einstrahlenden Schwarzkörpereinsatzes im Rohrofen abhängig ist.
- und dass diese Leistungsdifferenz durch die Thermosäule in der Sonde (ein Thermoelement mit einer der einfallenden Strahlung zugewandten als schwarzer Körper ausgebildeten Oberfläche an einem der beiden Pole) als ein Spannungssignal UT gemessen werden kann, dass zur Leistungsdifferenz direkt proportional ist und ebenfalls mit Hilfe der Messeinrichtung fortlaufend protokolliert werden kann.
Das Verständnis der Funktionsweise des als Detektor dienenden Thermoelements ist für die SuS nicht erforderlich - das betrifft insbesondere die Erwärmung der Schwarzkörperseite des Thermoelements über TR proportional zur aufgenommenen Strahlungsleistung.
Damit ist es den SuS möglich, die Bedeutung der Größe ΔT = TR - T0 (die Temperaturdifferenz zwischen Schwarzkörpereinsatz und Thermosäule nach Moll) im Zusammenhang mit dem Versuch zu verstehen und im Zuge der Auswertung der Versuchsergebnisse in der grafischen Darstellung der Messwerte den Zusammenhang zu erkennen.
In der Auswertung sollten die SuS dahin gebracht werden, mit Hilfe der entsprechenden Diagramme den nicht linearen Zusammenhang der beiden Größen selbst und in der Folge einen linearen Zusammenhang zwischen der Thermospannung (als Maß für die absorbierte Strahlungsleistung) und der Differenz der vierten(!) Potenz der Temperaturen der beiden schwarzen Körper zu erkennen und möglichst auch zu erfassen, wie diese formale Beschreibung in Bezug auf das beobachtete Phänomen zu interpretieren ist (ggf. in Analogie zur beschleunigten Bewegung mit linearem Zusammenhang zwischen Weg und Quadrat der Zeit als ein Muster für einen nicht linearen Zusammenhang).
In einem nächsten Schritt kann anhand des Diagramms, in dem ja Abweichung der Messwerte von der Ausgleichsgeraden (also der mathematische Formulierung des Zusammenhangs) offensichtlich sind, eine Fehlerdiskussion geführt werden.
Versuchsanleitung
Der Versuch wird in der hier beschriebenen Form mit Materialien der Fa. Leybold (LEYBOLD DIDACTIC GMBH) aufgebaut und durchgeführt. Aufbau, Durchführung und Auswertung werden in der Anleitung der Fa. Leybold [5] ausführlich beschrieben. Diese ist über das Internet frei zugänglich, so dass sie hier nur verlinkt (siehe [2] [22.03.2015]) und auf eine vollständige Wiedergabe von Einzelheiten wie z. B. der Bedienung der Geräte verzichtet wird.
Für die Messwerterfassung wird das Cassy-System der Fa. Leybold, angeschlossen an einen PC bzw. einen Laptop, benutzt. Die Messwerte können in ein Tabellenkalkulationsprogramm wie OpenOffice oder Excel exportiert werden. Da es verschiedene Versionen der Geräte und der zugehörigen Software gibt und diese nicht spezifisch für den beschriebenen Versuch sind, wird hier für die Anwendung des Cassy-Systems nur auf die Herstellerseite (siehe [3] Leybold) verwiesen.
Nachfolgend werden alle wesentlichen Aspekte beschrieben, teilweise in Anlehnung an oder als Auszug aus der Anleitung der Fa. Leybold, nachfolgend „Anleitung-Leybold“ genannt.
Materialien
Versuchsträger
- 1 Großer Stativfuß, V-förmig (Leybold, ArtNr. 300 01)
- 1 Universal-Stativklemme S (Leybold, ArtNr. 666 555)
- 1 Kleine Optische Bank (Leybold, ArtNr. 460 43)
- 4 Leybold-Muffen (Leybold, ArtNr. 301 01)
Beheizbarer Schwarzer Körper
- 1 Rohrofentisch (Leybold, ArtNr. 555 84)
- 1 Elektrischer Rohrofen (Leybold, ArtNr. 555 81) (siehe [4] [14.03.2015])
- 1 Schwarzkörperzusatz (mit Blende) (Leybold, ArtNr. 389 43) (siehe [5] [14.03.2015])
- 1 Temperaturfühler NiCr-Ni (Leybold, ArtNr. 666 193) (siehe [6] [15.03.2015])
Schwarzer Körper mit Raumtemperatur, mit Detektor für Infrarot-Strahlungsleistung
- 1 Thermosäule nach Moll (Leybold, ArtNr. 557 36) (siehe [7] [15.03.2015])
Messwerterfassung:
- 1 CASSY-Pack-E (Leybold, ArtNr. 524 007)
- 1 Temperatur-Box (NiCrNi/NTC) (Leybold, ArtNr. 524 045)
- 1 Amplifier-Box (Leybold, ArtNr. 525 055)
- 1 Disk.: Universelle Meßwerterfassung (Leybold, ArtNr. 525 031)
- zusätzlich erforderlich: PC mit Windows ab 3.1 oder Windows 95
Weiteres Zubehör
- Experimentierkabel
Aufbau
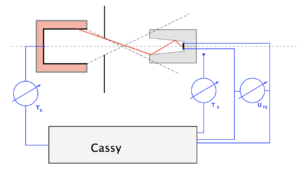
Zum Verständnis der nachfolgenden Ausführungen wird eine schematische Darstellung des Versuchsaufbaus gezeigt. Eine detaillierte Zeichnung ist in der Anleitung enthalten.
Die Anschlüsse zur Spannungsversorgung von Messgeräten und Ringofen sind aus Gründen der Übersichtlichkeit nicht enthalten, ebenso der Anschluss des Cassy-Systems an einen Computer.
Auf der optischen Bank sind (von links nach rechts, vgl. Anleitung-Leybold) folgende Geräte montiert:
- Temperaturfühler NiCr-Ni, über die Temperatur-Box angeschlossen an das Cassy-System, zur Messung der Temperatur des Ringofens.
- Elektrischer Rohrofen, beheizbar in einem Bereich von 300 K bis 700 K: im Inneren des Rohrofens befindet sich der „Schwarzkörperzusatz“ der Fa. Leybold - ein Körper aus einer Legierung, deren Strahlungsemission der eines idealen schwarzen Körpers für diesen Versuch ausreichend nahe kommt.
- Blende (bei Leybold Teil des Artikels „Schwarzkörperzusatz“) aus Metall mit einer definierten Öffnung für die von dem schwarzen Körper emittierte Infrarotstrahlung. Diese Blende ist hohl und kann optional mit Wasser im Durchfluss gekühlt werden, um zu verhindern, dass bei langen Versuchsdauern die Blende erwärmt und damit selbst zur undefinierten Strahlungsquelle wird. Das ist z. B. mit (in der obigen Liste nicht aufgeführtem) Zubehör der Fa. Leybold möglich. Zu- und Abfluss sind in der Anleitung-Leybold dargestellt.
- Thermosäule nach Mollbestehend aus in Reihe geschalteten Thermoelementen in einem Metallgehäuse. Die Oberfläche des einen Pols stellt einen (annähernd) idealen schwarzen Körper dar, während die andere Seite über die Verbindung mit dem Metallgehäuse auf Raumtemperatur gehalten wird. Die Thermosäule ist in dem Metallgehäuse am Ende einer konischen Öffnung mit polierter Oberfläche so angebracht, dass die gesamte durch die Blendenöffnung (annähernd parallel zur optischen Achse) einfallende Infrarotstrahlung direkt oder nach Reflexion am Konus auf die schwarze Fläche des Thermoelements trifft, während seitlicher einfallende Streustrahlung nach mehrfacher Reflexion wieder durch die Öffnung austritt. Die Thermosäule ist zur Messung der Thermospannung über die Amplifier-Box ebenfalls an das Cassy-System angeschlossen.
Durchführung
Für die Details der Bedienung von Ofen, Thermosäule und Cassy-System mit Messgeräten und Computer wird auf die Anleitung-Leybold verwiesen. Der Versuchsablauf ist folgender:
Der Rohrofen wird zunächst bis zur gewünschten maximalen Temperatur aufgeheizt, danach wir die Heizung abgeschaltet und der Rohrofen mit Schwarzkörpereinsatz kühlt sich wieder bis auf Raumtemperatur ab. Die Messung ist prinzipiell sowohl während der Aufheiz- wie auch während der Abkühlphase möglich. Da zu Beginn der Aufheizung bzw. der Abkühlung instationäre Randbedingungen möglich sind (z. B. Erwärmung der Heizwendel, bevor das Ofeninnere erwärmt wird, Restwärme der Heizwendel, bevor der Ofen ungestört abkühlt), sollte die eigentliche Messung erst gestartet werden, wenn sich die Temperatur des Rohrofens bereits um 5 K gegenüber der Starttemperatur verändert hat. Bei erreichen der unteren (bzw. oberen) Temperaturgrenze wird die Messung beendet, die Messwerte werden gespeichert.
Die Aufheizphase dauert nur ca. 45 - 60 Minuten, so dass nahezu über den gesamten Temperaturbereich gemessen werden kann. Dafür besteht lt. Anleitung die Gefahr einer Störung der sehr empfimdlichen Messung der Thermospannung durch Störimpulse der Heizung des Rohrofens, die über die gemeinsame Stromversorgung übertragen werden können. Bereits die Abkühlung des Rohrofens bis auf 100 °C bzw. 375 K dauert ca. 90 - 120 Minuten - die Fortsetzung der Messung bis in den Bereich der Raumtemperatur dauert aufgrund des exponentiellen Verlaufs unverhältnismäßig lange. Die ungestörte Messung bedingt so den Nachteil des verringerten Temperaturbereichs, über den gemessen werden kann.
Wenn die Priorität bei der Erzielung möglichst ungestörter Messwerte liegt, sollte die auszuwertende Messung während der ungestörten Abkühlphase erfolgen. Wenn die Priorität bei der möglichst überzeugenden Darstellung des nicht linearen Zusammenhangs liegt, sollte ein möglichst großer Temperaturbereich angestrebt werden.
Da die Versuchsdauer in jedem Fall den Zeitrahmen von Unterrichtsstunden sprengt, sollte zur Vorführung des Versuchs die Aufheizphase (bzw. ein Teil davon) genutzt und zur Auswertung auf zuvor aufgezeichnete geeignete Messwerte ausgewichen werden.
Bereits während der Messung können die bei dem aktuellen Versuchslauf bereits gesammelten Messwerte mit Hilfe des Cassy-Systems und des PC z. B. als Diagramm per Beamer gezeigt und so von den SuS mitverfolgt werden. Dies ist für die SuS auch die einzige Möglichkeit, den Versuchsablauf zu beobachten.
Ergebnisse
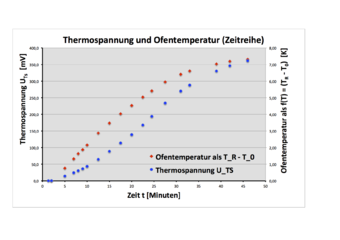
Es werden die drei Parameter Zeit t, Thermospannung UTR und Ofentemperatur TR gemessen und protokolliert. Damit lassen sich der zeitliche Verlauf der Thermospannung UTS und der Differenz zwischen Ofentemperatur und Raumtemperatur ΔT = TR - T0 grafisch darstellen (s. Bild 2).
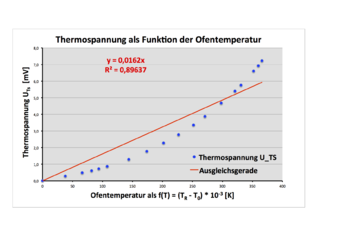
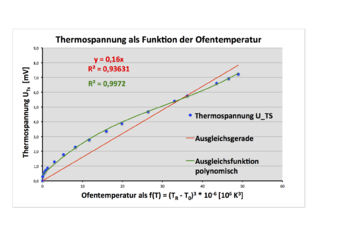
Die Auftragung der Thermospannung UTS über die Ofentemperatur ΔT = TR - T0 (s. Bild 3) zeigt diese beiden Größen in Relation zueinander.
Auswertung
Die Auftragung der Temperatur über die Zeit in Bild 2 zeigt einen Temperaturanstieg, der sich asymptotisch einer oberen Grenze nähert - diese ist erreicht, wenn die Heizleistung und die Wärmeverluste des Rohrofens sich ausgleichen. Die Thermospannung steigt zunächst überproportional an, mit dem Abflachen der Temperaturkurve nähert sich auch die Thermospannung asymprotisch einem konstanten Wert an. Die Beziehung zwischen diesen beiden Größen ist nicht offensichtlich.
Die Auftragung der beiden Größen in dem UTS - ∆T-Diagramm (s. Bild 3) zusammen mit einer rechnerisch ermittelten und ebenfalls in das Diagramm eingetragene Ausgleichsgeraden mit k = 0,0159 mV/K zeigt, dass zwischen den Größen kein linearer Zusammenhang der Form
- mit
besteht. In Analogie zum Weg-Zeit-Gesetz für beschleunigte Bewegungen lässt sich vermuten, dass auch hier ein linearer Zusammenhang vorliegen könnte, wenn statt TR und T0 Potenzen dieser Größen eingesetzt werden.
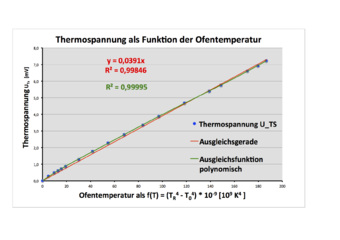
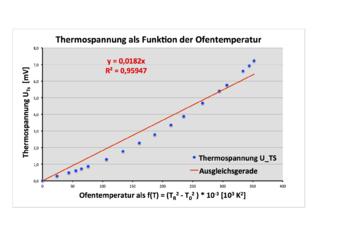
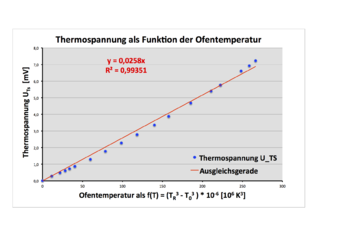
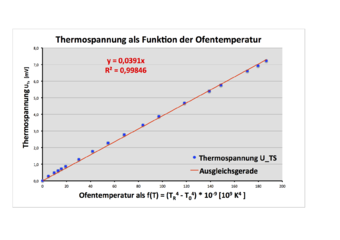
Mit der 2., 3. und 4. Potenz dieser Größen ergeben sich die in den Bildern 4, 5 und 6 dargestellten Diagramme, in die zusätzlich die Ausgleichsgeraden eingefügt sind, die (unter Annahme eines jeweils linearen Zusammenhangs) gleichzeitig die entsprechende mathematische Modellierung abbilden. Es zeigt sich, dass eine mathematische Beschreibung mit der 4. Potenz der Temperaturen die beste Übereinstimmung ergibt und somit ein (annähernd) linearer Zusammenhang besteht:
Darin ist k = 0,0387 mV/K4 die Steigung der Ausgleichsgeraden. Diese stimmt mit R2 = 0,99748 gut mit der Punktereihe überein.
Damit ist die pro Flächeneinheit abgegebene Strahlungsleistung (in guter Näherung) proportional zur 4. Potenz der Temperatur, und mit dem Kennwert der Thermosäule W = 0,16 (mV)/(mW) gem. Herstellerangabe ergibt sich für die Konstante zunächst die Einheit
- .
Wenn durch eine veränderte Geometrie der Versuchsanordnung unter sonst gleichen Bedingungen die Strahlungsleistung einer z. B. zweifach größeren Fläche eines Schwarzkörpereinsatzes auf die Thermosonde fallen würde, wäre die (zum Überschuss der Strahlungsleistung proportionale) gemessene Thermospannung UTS um diesen Faktor größer, d. h. die Strahlungsleistung ist proportional zur Fläche. Damit ergibt sich letztlich als Einheit für die Konstante k
- .
Dies ist die Einheit der Stefan-Boltzmann-Konstante σ in dem von Stefan Boltzmann gefundene Zusammenhang
zwischen der von einer Oberfläche abgegebenen flächenbezogenen Strahlungsleistung M und ihrer Temperatur (der Zahlenwert von k und σ kann nicht übereinstimmen, da in k auch die nicht näher spezifizierte Geometrie der Versuchsanordnung eingeht).
Da schwarze Körper auch einfallende Strahlung absorbieren, gilt das Stefan-Boltzmann-Gesetz korrekt nur, wenn keine Umgebungsstrahlung auf diesen Körper einfällt (keine anderen strahlenden Oberflächen bzw. Umgebung bei 0 K). In einem realen Versuch ist die absorbierte Umgebungsstrahlung zu subtrahieren - es wird eine Strahlungsbilanz aufgestellt. Für den betrachteten Versuch mit der flächenbezogenen Strahlungsleistung des betrachteten Körpers PK = σ TK4 (im Versuch der Rohrofen) und der umgebenden Fläche auf Raumtemperatur P0 = σ T04 gilt so:
und unter Berücksichtigung der unbekannten Geometrie der Versuchsanordnung gilt die Proportionalität
Damit wird der aus der mathematischen Modellierung der Messwerte gefundene Zusammenhang auch durch physikalische Betrachtungen plausibel.
Im Physikunterricht können Versuche mit höheren oder niedrigeren Temperaturen nicht durchgeführt werden. Unter der Annahme, dass dieses Ergebnis auch auf die Temperaturbereiche außerhalb der Messungen extrapoliert werden kann, erhält man durch Einsetzen einer Umgebungstemperatur von T0 = 0 K
und damit den von Stefan Boltzmann gefundenen Zusammenhang.
In den Bildern 7 und 8 wird die Thermospannung U_TS nicht über die Differenz der Potenzen der Temperaturen, sondern über die Potenz der Differenz der Temperaturen aufgetragen:
anstatt
sowie
anstatt
Auch diese Auftragungen sind mathematische Modellierungen, die mit den SuS diskutiert werden können - mit dem Ergebnis, dass sie die Messwerte schlechter repräsentieren als die Auftragung in Bild 6.
Diskussion der Ergebnisse
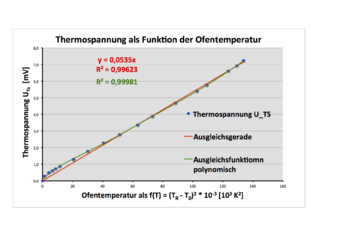
Die mathematische Modellierung, wie sie in Bild 6 gezeigt wird, zeigt in guter Näherung einen lineren Zusammenhang. Bei genauerer Betrachtung sind jedoch Abweichungen erkennbar. Die Auftragung in Bild 9 entspricht derjenigen in Bild 6, zeigt jedoch zusätzlich eine polynomische Ausgleichsfunktion (6. Grades), die die Messwerte noch besser beschreibt. Durch (im Rahmen des Schulunterrichts nicht mögliche) weitere Versuche, die genauer und/oder in anderen Temperaturbereichen durchgeführt werden, ließe sich zeigen, dass der Zusammenhang mit (TR4-T04) reproduziert werden kann, die weiteren Abweichungen aber auf systematischen Fehlern beruhen. Mit den SuS kann darüber diskutiert werden, wie sich z. B. Störungen durch Konvektion an der Thermosonde nach Moll oder störende Wärmestrahlung aus der Umgebung des Ofens oder durch die im Versuchsverlauf erwärmte Blende auf den Verlauf der Auftragung auswirken können und dass sie somit eine mögliche Erklärung für die beobachtbaren Abweichungen darstellen (was theoretisch durch weitere, modifizierte Versuche ggf. bestätigt werden könnte).
Die mathematische Modellierung könnte z. B. zur Auslegung der Heizleistung einer Strahlungsheizung sein. Eine Versuchsreihe z. B. mit einem Leslie-Würfel (in einer anderen Unterichtseinheit) würde die Bedeutung der Qualität der Oberfläche (blank - farbig - mattschwarz) auch für die Emission von Wärmestrahlung zeigen und damit auch die Einschränkung, die das Modell aufgrund der Annahme eines idealen schwarzen Körpers hat (für die Absorption ist diese Einschränkung aus dem Alltag bekannt - jeder weiß, dass sich schwarze Flächen bei Bestrahlung mehr erwärmen als weiße oder blanke).
Die Bedeutung solcher Erkenntnisse zur Prognose von Phänomenen lässt sich dann im Kontext z. B. von Wetterprognosen und Klimamodellen verdeutlichen, womit auch wieder der Rückbezug auf reale Phänomene möglich ist.
Sicherheitshinweise
Beim Anschluss der Rohrofens und der Spannungsversorgung für die Messungen sind die Vorsichtsmaßnahmen beim Umgang mit Netzspannung zu beachten.
Achtung: Die Außentemperatur des Rohrofens kann Temperaturen über 200 °C erreichen. Es ist daher auf eine sichere Montage des Rohrofens gemäß Gebrauchsanweisung zu achten, Berührungen des heißen Rohrofens sind zu vermeiden. Es ist darauf zu achten, dass keine Kabel, Abdeckungen oder andere Gegenstände den Rohrofen berühren oder auf ihn fallen oder kippen können.
Literatur
- ↑ Senatsverwaltung für Bildung, Jugend und Sport: Berliner Rahmenlehrplan SEK II, verfügbar unter [1] ,
- ↑ Burkhard Priemer, Vorlesung: Einführung in die Didaktik der Physik, Lehren und Lernen
- ↑ Kircher, Girwidz, Häußler: Physikdidaktik
- ↑ Burkhard Priemer, Vorlesung: Einführung in die Didaktik der Physik, Modelle und Analogien im Physikunterricht
- ↑ Anleitung der Fa. Leybold: P5.5.2.2 Stefan-Boltzmann-Gesetz: Temperaturabhängige Messung der Strahlungsintensität eines „Schwarzen Körpers“ Aufzeichnung und Auswertung mit der Universellen Meßwerterfassung (gefunden am 09.12.2013)
Siehe auch
- Leybold: Cassy-System; http://www.ld-didactic.de/service/softwaredownload/cassy-s.html [22.03.2015]
 Dies ist die
Dies ist die 




![{\displaystyle [k]={\frac {W}{K^{4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc7eb5d9ec37d108f63d9d6143da0880cb36ce21)
![{\displaystyle [k]={\frac {1}{m^{2}}}\cdot {\frac {W}{K^{4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21215bdc1ec2615980f08caaf051cf70b27d82c2)