Vermessung des Feldes eines (Hufeisen-)Magneten

Vermessung des Feldes eines (Hufeisen-)Magneten
Abb. [1]: Bild des vermessenen Magneten und der verwendeten Hall-Sonde, angeschlossen an ein Teslameter
Kurzbeschreibung
Quantitative Messung orthogonaler Komponenten des Magnetfeldes eines Hufeisenmagneten in einer Ebene
Kategorien
Elektrizitätslehre, Magnetismus
Einordnung in den Lehrplan
Geeignet für:	Sek. I Jahrgangsstufe 7/8
Basiskonzept:	Wechselwirkung
Sonstiges
Durchführungsform	Lehrerdemoexperiment, Schülerdemoexperiment, Schülerexperiment
Anspruch des Aufbaus	einfach
Informationen
Name:	Christopher Wolf
Kontakt:	${\text{cwolf}}$@${\text{physik.hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Steffen Wagner

Der in diesem Artikel beschriebene (und in Abb. [1] dargestellte) Versuch eignet sich in besonderer Weise als Einstieg in das Themengebiet der Magnetostatik, da keinerlei physikalische Voraussetzungen seitens der Schülerschaft erfüllt sein müssen und er eine sehr gute Einführung in das Modell des magnetischen Feldes bietet. Auf die im Zuge dieses Experimentes gewonnenen Kenntnisse, Vorstellungen und Kompetenzen kann bei der Einführung des Modells der elektrischen Feldlinien aufgebaut werden.
Der Versuch Vermessung des Feldes eines (Hufeisen-)Magneten ist simpel im Aufbau (Zeitaufwand ≈ 5 Minuten), überschaubar bis aufwendig in der Auswertung und wertvoll für ein tiefgreifenderes Verständnis der Magnetostatik.

Didaktische Analyse zum Modell

Felder sind ein wichtiges und in der Physik sehr weit verbreitetes Konzept, das dabei hilft, die räumlichen Auswirkungen von Wechselwirkungen zu erfassen. Insbesondere sind sie ein effektives Hilfsmittel "wenn es darum geht, die Auswirkungen von physikalischen Größen zu studieren, die an verschiedenen Orten unterschiedliche Werte annehmen". Im Physikunterricht werden Felder implizit durch die Betrachtung von Feldlinien deshalb schon frühzeitig verwendet.
Aufgrund der großen Bedeutung des Konzeptes des Feldes scheint die Frage lohnenswert, wie dieses unterrichtet werden kann und welches Modell konkret eingeführt wird. Häufig fällt dabei die Wahl auf das klassische und sehr weit verbreitete Feldlinienmodell.
Die verbreiteten Feldlinienmodelle dienen der Visualisierung von Größen und Wechselwirkungen, die nicht direkt beobachtbar sind. Dabei wird im Allgemeinen die Stärke des Feldes durch die Dichte der Feldlinien ausgedrückt, welche imaginäre Linien sind, entlang derer sich der Nordpol einer Probe ausrichten und bewegen würde. Dass das Feld, das an sich wiederum nur ein Modell ist, nicht direkt beobachtet werden kann wird es durch weitere Modelle oder Visualisierungen dargestellt, wie zum Beispiel durch mathematische Formulierungen (die Maxwell-Gleichungen, etc.) oder anderweitige Veranschaulichungen (Feldlinienmodelle, Magnetnadelmodelle, etc.). Dabei sind Feldlinienbilder eine sehr simple und intuitiv zugängige Darstellung von Vektorfeldern, die in den Schulen zumeist primär genutzt wird. Jedoch werden Feldlinien im Schulalltag häufig unpräzise verwendet, beispielsweise ist die Feldliniendichte häufig nicht proportional zur Feldstärke. Auch die genaue Entstehung des Verlaufes der Feldlinien ist vielmals nicht nachvollziehbar. Oft bleibt ungeklärt, wie die Feldlinien im Inneren des Magneten verlaufen und wie sich das Feld zwischen ihnen verhält. Des Weiteren ist für den Betrachter nicht sofort nachvollziehbar, wie es in einer Grafik zu der Auswahl der endlich vielen abgedruckten Feldlinien kam und was zwischen ihnen liegt. Die Vorstellung von Feldlinien ist demnach für das Verständnis von Magnetismus durchaus dienlich, birgt aber für den Schüler (besonders in der Anwendung) einige Schwierigkeiten.
Im beschriebenen Versuch wird durch das Abtasten des wirkenden Magnetfeldes mit einer Hall-Sonde an festgelegten Messpunkten das magnetische Feld exemplarisch untersucht. Dabei sollte durch dynamisches Verschieben der Sonde sichtbar sein, dass das Feld auch zwischen den Messpunkten existiert. Das so erhaltene Modell, ein Magnetnadelbild bestehend aus einzelnen das Feld repräsentierenden Pfeilen, ist durch den Schüler haptisch erlebt worden. Es sollte unbedingt darauf geachtet werden, dass dem Schüler klar ist, wie die Länge und die Richtung der Pfeile direkt aus den an den abgetasteten Punkten gemessenen Feldstärken resultieren. Auch die Festlegung des abzutastenden Rasters (und dessen Beliebigkeit) sollten thematisiert werden und es sollte demonstriert werden, dass Messungen auch an allen anderen Punkten durchgeführt werden können. Dadurch kann auch verdeutlicht werden, wie stark ein Modell von Festlegungen und Grundannahmen abhängt. Bei der Auswertung sind die Bedeutung der Pfeile, deren Länge, Richtung und Dichte, sowie die Bedeutung des Zwischenraumes zwischen den Pfeilen dem Schüler bekannt.
Aufgrund dessen nimmt das Magnetnadelmodell, insbesondere wenn es (wie hier) ausgiebig eingeführt worden ist, verdientermaßen einen wichtigen Platz neben dem klassischen Feldlinienmodell ein. Dabei muss bei beiden Modellen selbstverständlich darauf geachtet werden, dass sie vom Schüler auch als die Realität innerhalb von Grenzen beschreibende Konstrukte wahrgenommen werden.

Versuchsanleitung

Der Versuch Vermessung des Feldes eines (Hufeisen-)Magneten ist im Aufbau sehr simpel und in der Durchführung ebenfalls einfach. Die Auswertung sollte an sich ebenfalls keine große Herausforderung darstellen, es sind jedoch teilweise sehr viele Messdaten einzutragen und auszuwerten.
In diesem Abschnitt sind zunächst die benötigten Materialien aufgelistet, wobei direkt im Anschluss Anmerkungen zu diesen und zur benutzten Software gemacht werden. Anschließend wird der Aufbau beschrieben, bevor abschließend die Durchführung geschildert wird, innerhalb derer auch auf Probleme bei der Versuchsdurchführungen eingegangen wird und eine Erweiterung des Versuchs in Aussicht gestellt wird.

Benötigte Materialien

• Ein Hufeisenmagnet (getestete Abmessung ca. 7 cm x 9 cm)
• Ein Din-A4-Blatt Millimeterpapier
• Ein Teslameter (inklusive Stromversorgung)
• Eine Hall-Sonde (inklusive Anschlusskabel zum Teslameter)
• Ein Computer
  • Microsoft Excel
  • GeoGebra

Anmerkung zu den benötigten Materialien

• Mit dem in diesem Artikel geschilderten Versuchsaufbau lässt sich prinzipiell das Magnetfeld jedes beliebigen Objektes aufnehmen (innerhalb der Sensibilität und Unsicherheit verwendeter Messgeräte). Insbesondere muss deshalb kein Hufeisenmagnet verwendet werden. Die Verwendung anderer (auch Hufeisen-)Magnete kann jedoch zu sehr stark abweichenden Ergebnissen führen.
• Die Funktionsweise der Hall-Sonde lässt sich mit dem Versuch zum Hall Effekt gut erläutern. Aufgrund des Aufwands, der Komplexität und der (deutlich späteren) Vorsehung im Rahmenlehrplan bietet es sich jedoch nicht an, diesen Versuch im gleichen Rahmen durchzuführen. Vielmehr wird empfohlen, die Hall-Sonde als sogenannte Blackbox zu verwenden.

Benötigte Software

• Zur Aufnahme und Aufbereitung der Messdaten wird ein Tabellenkalkulationsprogramm benötigt. Zwar weisen die meisten verbreiteten Tabellenkalkulationsprogramme (wie z.B. Numbers (iWork), Calc (Libre Office), etc.) die benötigten Funktionen auf, aufgrund persönlicher Präferenzen ist jedoch Excel (Microsoft Office 365) verwendet worden.
• Für die Darstellung der Messdaten ist die dynamische Geometrie-Software GeoGebra verwendet worden. Diese ist kostenfrei über die in Siehe auch verlinkte Seite beziehbar.

Aufbau

Abb. [3]: Beispiel für ein auf Millimeterpapier erstelltes Raster mit Positionsmarkierung des Magneten.

Der Aufbau des Versuches ist sehr simpel und erfolgt in 9 Schritten:

• Zunächst wird der Magnet mittig auf dem Millimeterpapier platziert und entschieden, wie viele Messpunkte in welchen Abständen von einander aufgenommen werden sollen.
• Die Position des Magneten auf dem Millimeterpapier wird markiert.
• Auf dem Millimeterpapier wird ein Raster eingezeichnet, anhand dessen die Messpunkte identifizierbar und leicht zu finden sind (wie in Abb. [3] dargestellt ist).
• Das Millimeterpapier wird an den für den Versuch ausgewählten Ort gelegt und der Magnet entsprechend der Markierung positioniert.
• Das Teslameter wird neben dem Millimeterpapier aufgebaut.
• Die Hall-Sonde wird an das Teslameter angeschlossen.
• Das Teslameter wird in Betrieb genommen und der angezeigte Wert auf 0 gesetzt (dafür befindet sich eine Buchse im Gerät, in die die Hall-Sonde währenddessen eingebracht wird).
• Der Computer wird bereitgestellt und das Tabellenkalkulationsprogramm geöffnet.
• In dem Tabellenkalkulationsprogramm wird eine neue Datei angelegt und vorbereitet, wie in der folgenden Tabelle dargestellt ist.

Für die Datenaufnahme vorbereitete Tabelle

A	B	C	D	E	F	G	H	I
Punkt	x-Koordinate	x-Wert	x normiert	x resultierend	y-Koordinate	y-Wert	y normiert	y resultierend
A_1	1		=C2*2/MAX($C$2:$C$121)	=B2-D2	1		=G2*2/MAX($G$2:$G$121)	=H2-F2
A_3	1		=C3*2/MAX($C$2:$C$121)	=B3-D3	3		=G3*2/MAX($G$2:$G$121)	=H3-F3
A_5	1		=C4*2/MAX($C$2:$C$121)	=B4-D4	5		=G4*2/MAX($G$2:$G$121)	=H4-F4
...	...	...	...	...	...	...	...	...

Die gegebene Tabelle ist für 120 aufgenommene Messpunkte ausgelegt. Sollten mehr Daten erfasst werden, muss diese selbstverständlicherweise erweitert werden. Dabei reicht es nicht, zusätzliche Zeilen einzufügen, sondern insbesondere muss in der Spalte D (x normiert) in der Formel =C2*2/MAX($C$2:$C$121) die Zahl 121 durch die Nummer der letzten belegten Zeile ersetzt werden. Analog muss die Spalte H (y normiert) angepasst werden.

Die vorherige Tabelle steht auch als Vorlage auch unter folgendem Link bereit:
Datei:Messdaten Vermessung Hufeisenmagnet.xlsx.
(Eine genauere Beschreibung der Funktionen der einzelnen Spalten erfolgt im Absatz Auswertung der Messdaten.)

Durchführung

Bei der Durchführung wird das Feld in den zuvor festgelegten Punkten, also entlang des eingetragenen Rasters, mit der Messspitze der Hall-Sonde abgetastet. Dabei wird für jeden Punkt die x-Komponente und die y-Komponente des Feldes aufgenommen. (Hierbei ist zu beachten, wie die Sonde gehalten werden muss. Im Normalfall steht bei der Hall-Sonde die größere Ausdehnung der Messspitze orthogonal zum Magnetfeld, bei verschiedenen Ausführungen kann dies aber unterschiedlich sein. Die genaue Funktionsweise der Hall-Sonde sollte deshalb in der zugehörigen Bedienungsanleitung nachgeschlagen oder in einem bekannten Feld "erprobt" werden.)
Die aufgenommenen Daten (x- und y-Komponente des Feldes) werden in der Tabelle unter den jeweiligen Koordinaten eingetragen.

Erweiterungen des Versuches

Untergrundmessungen

Um präzisere Ergebnisse zu erhalten, kann eine Untergrundmessung durchgeführt werden. Dabei wird das Raster ohne darauf befindlichem Magneten abgefahren und die Feldstärken aufgenommen. Anschließend wird die Messung wie in Aufbau beschrieben vorgenommen. Von den erhaltenen Messwerten werden die Messwerte der jeweils gleichen Punkte aus der Untergrundmessung subtrahiert. Die daraus resultierenden Werte sind von dem Hintergrundfeld bereinigt.
Bei stichprobenhaften Tests in der Vorbereitung wurde jedoch festgestellt, dass Hintergrundfelder im Allgemeinen vernachlässigbar sind.

Dreidimensionale Untersuchungen

Das Feld des untersuchten Magneten kann selbstverständlich auch dreidimensional im Raum abgetastet werden. Dabei werden jedoch deutlich mehr Messdaten generiert und insbesondere das präzise und reproduzierbare Anfahren einzelner Messpunkte ist problematisch. Für gewöhnlich rechtfertigt der gesteigerte Erkenntnisgewinn den höheren Aufwand nicht.

Sicherheitshinweise

Für die Versuchsdurchführung sind keinerlei besondere Sicherheitshinweise zu beachten (abgesehen von den normalen Maßnahmen die getroffen, werden wenn mit Netzspannung betriebene Geräte verwendet werden).

Ergebnisse

Bei dem gegebenen Versuch muss erst eine detaillierte Auswertung der Messdaten erfolgen, bevor die Messergebnisse sinnvoll betrachtet werden können. Die Auswertung der Messdaten ist durch die Präparation der Tabelle und das Einfügen der Daten in diese (siehe Durchführung) bereits begonnen. Die Funktionsweise der Tabelle und die grafische Aufarbeitung der Messdaten sind im folgenden Unterkapitel Auswertung der Messdaten geschildert.

Auswertung der Messdaten

Einer der Hauptbestandteile dieses Versuches ist die sorgfältige Auswertung der bei der Durchführung gewonnen Daten. Diese sind mit einem Tabellenkalkulationsprogramm aufgenommen worden und werden mit Hilfe der dynamischen Geometrisoftware Geogebra dargestellt. Dabei wird das Tabellenkalkulationsprogramm auch dazu genutzt, die Messdaten so zu berechnen, dass sie gleich zur grafischen Darstellung des Feldes genutzt werden können.

• In der Tabelle (nach der Form, die hier zur Verfügung gestellt worden ist) steht in der Spalte A die Bezeichnung des Messpunktes. Dies dient nur der Orientierung und eindeutigen Identifikation.
• In der Spalte B wird die x-Koordinate des Punktes angegeben.
• Die Spalte C listet die jeweils gemessenen Werte für die x-Komponente des Magnetfeldes auf.
• In der Spalte D werden die Messwerte aus der vorherigen Spalte auf 2 normiert. Damit hat später der Pfeil mit der größten x-Komponente eine Ausdehnung von 2 Längeneinheiten in x-Richtung (oder entgegengesetzt). Die Normierung auf 2 ist gewählt worden, da alle 2 cm gemessen wurde. Andere Normierungen sind möglich und können sinnvoll sein.
• Die Spalte E erzeugt durch Substraktion die x-Koordinate des Endpunktes eines Pfeiles, der von einem Punkt mit der in B angegeben x-Koordinate aus die x-Komponente des Magnetfeldes normiert darstellt.
• Analog wird in den Spalten F bis I für die y-Komponente des Magnetfeldes verfahren.
• In den Spalten B und F stehen die Koordinaten des untersuchten Punktes $P_{i}$.
• Aus den Spalten E und I erhält man die Koordinaten der für die Darstellung benötigten Hilfspunkte $P'_{i}$.

Zur Darstellung werden nun in GeoGebra die Punkte $P_{i}$ und $P'_{i}$ erstellt. Anschließend wird auf den Befehl "Vektor", den Punkt $P_{i}$ und den Punkt $P'_{i}$ geklickt. Dadurch wird in der Darstellung ein Pfeil (als Darstellung des Vektors) vom Punkt $P_{i}$ zum Punkt $P'_{i}$ erzeugt. Die beiden Punkte können nun ausgeblendet werden.
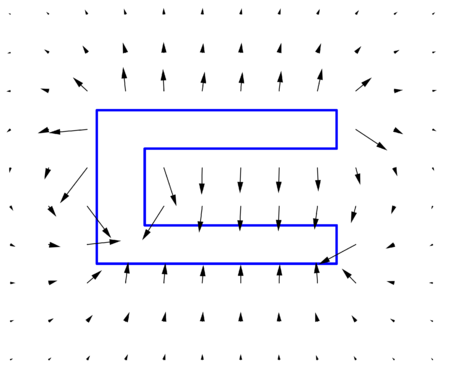
So werden für alle Messpunkte die zugehörigen Pfeile erzeugt, die in der Darstellung die Ausrichtung und Stärke des Magnetfeldes symbolisieren.
Als konkretes Beispiel seien folgende Messdaten gegeben: Messdaten
Aus ihnen kann nach der hier beschriebenen Vorgehensweise die Abbildung [4] erstellt werden.

Interpretation der Ergebnisse

Abb. [4]: Darstellung der ausgewerteten und umgerechneten Messergebnisse und der Lage des Magneten in einer Grafik.

Die bei der Durchführung erhaltenen Ergebnisse dienen bei diesem Versuch dem Erstellen einer Grafik (Abb. [4]). Diese stellt ein so genanntes Magnetnadelmodell des Feldes dar. Dabei steht jeder Pfeil für die Orientierung (repräsentiert durch die Richtung des Pfeiles) und die Stärke (repräsentiert durch die Länge des Pfeiles) des Feldes.
Anders als beim Feldlinienmodell werden keine modellierten Feldlinien durchgehend gezeichnet, sondern ein regelmäßiges Raster abgetastet. Während es dadurch schwieriger ist, Bereiche gleich stark wirkendenden Magnetfeldes zu erfassen bietet es weniger Raum für Fehlvorstellungen. Durch das durchgeführte Abtasten beliebiger Punkte ist es verständlich, dass zwischen den erhaltenen Pfeilen auch ein Magnetfeld wirkt, während zwischen den Feldlinien teilweise ein feldfreier Raum vermutet wird. Des Weiteren kann, im Gegensatz zu Darstellungen der Feldlinien, die Stärke des Magnetfeldes (und somit auch deren Abfall) beurteilt werden.
Ein Manko ist hingegen, dass das Feld im Inneren des Magneten nicht abgetastet werden kann und deshalb in der erstellten Grafik nicht eingetragen ist. Eine Vorstellung davon kann nicht direkt durch diesen Versuch aufgebaut werden und muss durch weitere Erklärungen und Versuche gestärkt werden ("Zerbteilen" eines Magneten, Aufbau eines Magneten, etc.). In höheren Klassenstufen und in ergänzenden Kursen können dazu auch die Weißschen Bezirke betrachtet werden.
Für ein umfassendes Verständnis des Feldes eine Magneten und dessen Verlauf im Raum zu Vermitteln scheint es jedoch sinnvoll zu sein, das Magnetnadelmodell und das Feldlinienmodell ergänzend zueinander zu lehren.

Umgang mit Messunsicherheiten

Auch wenn die erstellte Abbildung eher phänomenologisch Auswirkungen und keine expliziten Zahlenwerte darstellt, kann auf eine Überlegung zu auftretenden Messfehlern nicht verzichtet werden.

Abb. [5]: Hilskonstruktion (Zerlegung eines Vektors in zwei Komponenten)

Die größte Unsicherheit liegt dabei beim manuellen Abtasten des Magnetfeldes. Es ist sehr schwer, die Hall-Sonde an jedem Messpunkt perfekt in x- bzw. y-Richtung auszurichten und in den meisten Fällen wird dadurch die jeweils andere Komponente mit gemessen. An Messorten, bei denen die x- und y-Komponenten des Feldes ähnlich stark ausgeprägt sind hat dies einen relativ geringen Einfluss auf die Messdaten und die zu erstellende Grafik. Bei Messpunkten, in denen die Komponenten eine sehr hohe Differenz haben (beispielsweise zwischen den Polen des Hufeisen des Magneten, wo ein relativ homogenes Magnetfeld mit Wirkung entlang der y-Richtung erwartet wird), kann bereits eine sehr geringe Fehlausrichtung der Sonde große Effekte haben. Dies ist auch in Abb. [4] sichtbar.

Abb. [6]: Hilskonstruktion (Einheitskreis)

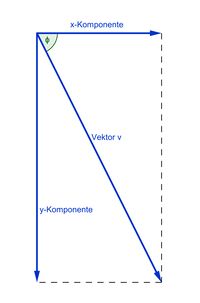
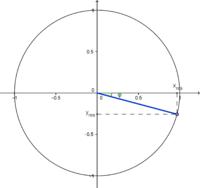
Die gemessene Größe setzt sich, wie in Abbildung 5 dargestellt ist, aus der x- und der y-Komponente des magnetischen Feldes in einem angelegten kartesischen Koordinatensystem an der betrachteten Stelle zusammen. Dabei gilt jedoch (aus trigonometrischen Betrachtungen (wie in Abbildung 6 dargestellt) und der Experimantalphysik bekannt), dass von den beiden Komponenten jeweils nur die Anteile $x_{res}=x\cdot \cos(\phi )$, bzw. $y_{res}=y\cdot \sin(\phi )$ wirken. Dies führt dazu, dass in einer Messung der Feldstärke parallel zur x-Achse (also für $\phi =0^{\circ }\Rightarrow \sin(\phi )=0$) der y-Anteil des Feldes null ist.
Bereits leichte Verdrehungen der Sonde können jedoch schon große Auswirkungen haben. Das lässt sich leicht zwischen den Stegen des Hufeisenmagneten sehen, wo ein homogenes Magnetfeld mit einer Ausrichtung parallel zum Verbindungsstück der Stege des Hufeisens erwartet werden darf. Insbesondere ist dies beim Messpunkt M9 (der obere und dritte Messpunkt von links zwischen den Stegen) der Fall. Während für die x-Komponente des Feldes der Wert 0 erwartet wird, wurde eine Ausprägung von 0.5 mT gemessen. Die y-Komponente wurde zu 14.2 mT bestimmt. Stellt man die angegebene Gleichung für die resultierende y-Werte um, so erhält man ${\frac {y_{res}}{y}}=\sin(\phi )\Rightarrow \arcsin({\frac {0.5}{14.2}})=\phi \Rightarrow \phi =2,02^{\circ }$. Dies bedeutet, dass die Messspitze lediglich um etwa 2° verdreht war und dies schon dafür ausreicht, deutlich sichtbare Abweichungen zu generieren. Bei dieser Rechnung ist davon ausgegangen worden, dass die y-Komponente des Feldes 14.2 mT betrug, was dem Messwert entspricht. Dabei ist davon auszugehen, dass auch dieser Messwert fehlerbehaftet ist und es zu einer Verdrehung kam, wodurch der eigentliche y-Wert als größer erwartet werden darf. Dadurch würde sich aber der errechnete Fehler in der Positionierung zur Messung der x-Achse wiederum etwas verringern.
Durch die Fehlausrichtung (Verdrehung) der Sonde kamen Abweichungen von bis zu 0,5 LE im Diagramm zu Stande. Andere Unsicherheiten, wie die des präzisen Anfahrens der Messpunkte, räumliche Ausdehnung der Messspitze, die Unsicherheit des Messinstrumentes und überlagernde Felder haben einen um Größenordnungen geringeren Einfluss.

Siehe auch

http://www.geogebra.org/

Berliner Rahmenlehrplan für das Fach Physik, Sekundarstufe I