Rutherford-Streuexperiment
| Rutherford-Streuexperiment | |
 Titelbild: Versuchsaufbau zur Durchführung des Rutherford-Streuversuchs | |
| Kurzbeschreibung | |
|---|---|
| Mit Hilfe der Streukammer des Lehrmittelherstellers Leybold-Didactic wird wird der Streuversuch nach Rutherford durchgeführt, um die Entwicklung des Rutherford'schen Atommodells nachzuvollziehen und die Abhängigkeit der Streuung der α-Teilchen vom Winkel und der Kernladungszahl des Targetmaterials experimentelle zu überprüfen. | |
| Kategorien | |
| Atom- und Kernphysik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II, 4. Kurshalbjahr |
| Basiskonzept: | Materie |
| Sonstiges | |
| Durchführungsform | Demonstrationsexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Michael Meyer |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Wiebke Musold |
Atome bilden die sichtbare Materie und sind selber nicht direkt beobachtbar. Über ihre Struktur bzw. ihren Aufbau müssen daher Theorien und Modellvorstellungen entwickelt werden, die wiederum durch Experimente überprüft werden.
Ernest Rutherford sowie seine Assistenten Hans Geiger und Ernest Marsden taten zwischen 1909 und 1913 genau dies. Sie wollten mit Hilfe ihres Streuexperimentes das 1903 von Joseph J. Thomson entwickelte Atommodell („Rosinenkuchen-Modell“) überprüfen, indem sie kollinear emittierte -Teilchen auf eine dünne Goldfolie (4μm) treffen ließen und die Streuung (Winkelverteilung) der -Teilchen mittels eines Fotoschirms beobachteten.
Nach dem Thomson’schen Atommodell hätten alle -Teilchen von der Goldfolie reflektiert werden müssen. Tatsächlich konnten nahezu alle -Teilchen die Goldfolie fast ungehindert durchdringen. Von 8000 -Teilchen wurde nur eines von der Goldfolie reflektiert.[1] Da bereits bekannt war, dass sich Gold nicht zusammenpressen lässt, die Goldatome also nebeneinander und in einigen Tausend Atomschichten übereinander angeordnet liegen, mussten die -Teilchen durch das Goldatom selbst geflogen sein.[2]
Die Ergebnisse interpretierte Rutherford innerhalb eines neuen, theoretischen Atommodells. Die grundlegende Annahme war, dass die gesamte positive Ladung und der überwiegende Teil der Atommasse in einem sehr kleinen Volumen im Zentrum komprimiert sein muss, an dem die -Teilchen gestreut werden. Aus der theoretischen Betrachtung heraus formulierte Rutherford auch die Formel, die die Streuung von -Teilchen an einer Metallfolie beschreibt:
mit
- : Anzahl gestreuter -Teilchen, pro Zeit- und Flächeneinheit am Ort des Detektors
- : Anzahl einfallender -Teilchen
- : Anzahl der Atomkerne pro Volumeneinheit der Streufolie
- : Dicke der Streufolie
- : Kernladungszahl des Folienmaterials
- : Kernladungszahl des -Teilchens
- : Elementarladung
- : Kinetische Energie der einfallenden -Teilchen
- : Abstand des Detektors vom Auftreffpunkt des einfallenden -Teilchens auf der Streufolie
Wegen seiner zentralen Stellung in der historischen Entwicklung der modernen Atomphysik als auch wegen des hinter ihm steckenden naturwissenschaftlichen Operation, einen (nicht sichtbaren) Sachverhalt mittels Modellentwicklung und Experiment zu erklären, machen das sogenannte Rutherford-Streuexperiment zu einem wertvollen Bestandteil des Physikunterrichts. Zudem lässt es sich Dank der durch die Lehrmittelhersteller zur Verfügung gestellten Streukammer auch sehr einfach im Unterricht umsetzen.
Inhaltsverzeichnis
Didaktischer Teil
Der Rutherford’sche Streuversuch und das von ihm abgeleitete Atommodell bildet historisch den Übergang zu unserer heutigen Atomvorstellung. Ebenso liefert er die physikalischen Grundlagen für eine Standardmethode der elementspezifischen Analyse von Festkörpern mittels Rutherford Backscattering Spectroscopy (RBS). Damit besitzt dieser Versuch einen großen Stellenwert sowohl für die Allgemein- als auch Fachbildung der Schülerinnen und Schüler.[3] Aber auch physikdidaktisch besitzt der Rutherford’sche Streuversuch großes Potenzial, indem mit seiner Behandlung im Unterricht auch ein Lernen mit und über Modell verknüpft werden kann.
Im Folgenden soll unter dem Begriff „Modell“ ein von einem Subjekt für bestimmte Zwecke und für eine bestimmte Zeit benutzter bzw. geschaffener Gegenstand oder theoretisches Konstrukt verstanden werden, dass zu bestimmten Elementen des zu erklärenden Objekts in Beziehung steht. Ein Modell ist damit kein exaktes Abbild des Objekts, sondern das Objekt kann Elemente enthalten, die im Modell keine Entsprechung findet. Speziell Atommodelle sollen daher als vorläufige Vorstellungen der Schülerinnen und Schüler bzw. vorläufige Hypothesen der Wissenschaft verstanden werden, die experimentell getestet werden und sich in bestimmten Bereichen bewährt haben.[4]
Ernst Kircher ist im Allgemeinen zuzustimmen, wenn er darauf hinweist, dass Physik lernen auch physikalische Modellbildung durch die Schülerinnen und Schüler bedeutet.[5] Auch die curricularen Vorgaben fordern das Arbeiten mit Modellen und das Verstehen der Modellhaftigkeit der Physik ein. So sollen die Berliner Schülerinnen und Schüler der gymnasialen Oberstufe beispielsweise im Themenfeld „Quantenobjekte und Struktur der Materie“ unter anderem Atommodelle quantitativ und qualitativ beschreiben, sie historisch einordnen und im historischen Kontext bewerten.[6]
Aber nicht erst in der Sekundarstufe II kommen die Schülerinnen und Schüler in Kontakt mit Modellen. Vielmehr lernen sie während ihrer gesamten Schullaufbahn unterschiedliche Arten physikalischer Modelle kennen. Dabei kommt es aber immer wieder zu Lernschwierigkeiten, die sich auf die folgenden drei Punkte zusammenfassen lassen:
- Bei der Untersuchung physikalischer Vorgänge und deren Erklärung vermengen die Schülerinnen und Schüler die Modell- und Realitätsebene. Als Folge entstehen „Hybridmodelle“, die sich dadurch auszeichnen, dass sie Eigenschaften aus der Lebenswelt in die zu modellierenden Bereiche übertragen.[7] Diese Übertragung von Eigenschaften der makroskopischen Welt auf die Mikrowelt zeigt sich z.B. in der Vorstellung, dass sich zwischen den Teilchen eines Stoffes Luft befindet, oder in der Dominanz des Planetenmodells bei der Atomvorstellung der Schülerinnen und Schüler, weil dieses zu ihrer mechanischen Denkweise passt.[8]
- Die Schülerinnen und Schüler verstehen unter einem Modell v.a. gegenständliche Modelle, was sich auch bei der Behandlung von Atommodellen nur bei wenigen Schülerinnen und Schülern kurzzeitig ändert.[9]
- Den Schülerinnen und Schülern ist der hypothetische Charakter von Modellen nicht bewusst.[10]
Schwierigkeiten beim Lernen von Physik treten demnach immer dann auf, wenn sich die behandelten Modelle widersprechen bzw. – als Ursache von Widersprüchen – unreflektiert mit der Modellvielfalt umgegangen wird. Daraus folgend plädiert nicht nur Siegfried Nöding dafür, den Modellierungsprozess an konkreten physikalischen Sachverhalten möglichst häufig zu üben, sondern auch angemessen viel Zeit für die explizite Diskussion der Erklärungsmächtigkeit und Grenzen von eingeführten Modellen aufzuwenden. Solch eine „Metadiskussion“ (Mikelskis-Seifert) kann folglich zum Verstehen des physikalischen Modellierungsprozesses, der physikalischen Phänomene selbst als auch zum Aufbau eines angemessenen Bildes von der Physik als Wissenschaft beitragen.[11]
Silke Mikelskis-Seifert hat eine „Modellmethode“ für das Lernen mit und über Modelle vorgeschlagen, in die sich auch der Rutherford’sche Streuversuch sehr gut integrieren lässt:[12]
- Einführungsphase: Sensibilisierung für die Modellproblematik, indem die Schülerinnen und Schüler den physikalischen Sachverhalt beobachten und zu dem Ergebnis gelangen, dass durch die direkt wahrnehmbaren Elemente des Versuchs/ Objektes keine physikalische Erklärung zu gewinnen ist. Der Versuch wird an dieser Stelle als Lehrerdemonstrationsexperiment durchgeführt.
Die Schülerinnen und Schüler sehen, dass die vom -Strahler (0°-Stellung in der Streukammer, d.h. senkrecht zur Goldfolie) emittierte Strahlung scheinbar ungehindert durch die Goldfolie tritt. Durch die makroskopische Untersuchung der Goldfolie sind keine Löcher in der Folie feststellbar. Es handelt sich um eine geschlossene, glänzende Oberfläche.
Die Phase endet mit der Feststellung, dass der Sachverhalt nicht aus sich selbst heraus erklärt werden kann, da die „wahre“ Struktur von Goldfolie und Strahlung nicht direkt wahrnehmbar ist. Nur die Verwendung eines Modells kann hier weiterhelfen. - Erarbeitungsphase: Modellentwicklung bzw. Modellauswahl, indem die Schülerinnen und Schüler Modellannahmen formulieren. Da die selbstständige Modellentwicklung durch die Schülerinnen und Schüler aufgrund des fehlenden fundierten physikalischen Hintergrundwissens nur sehr eingeschränkt erfolgen kann, sollten hier die Atommodelle von Leukipp und Demokrit (ca. 400 v. Chr.), von Dalton (ca. 1800) und schließlich von Thomson (ca. 1900) herangezogen werden,[13]um sie auf ihre Tragfähigkeit und ihren Erklärungswert bezogen auf den beobachteten Sachverhalt zu prüfen.
Als Ergänzung könnten die Schülerinnen und Schüler Modellexperimente heranziehen, wo sie selbstständig z.B. in kleinen Gruppen die Tragfähigkeit ihrer Modellannahmen überprüfen. Der Luftkissentisch bietet sich hier besonders an. Im Falle des Thomson’schen Atommodells können die Schülerinnen und Schüler mit Hilfe kleiner Magneten eine kompakte Atomschicht (d.h. ohne Zwischenräume) nachbilden und dann visuell beobachten, wie sich ein -Teilchen (durch einen weiteren, kleinen Magneten nachgebildet) verhält, dass auf solch eine Atomschicht trifft.[14] Die Schülerinnen und Schüler würden Totalreflexion beobachten, was allerdings nicht der experimentellen Beobachtung entspricht.
Nach den Untersuchungen auf der Realitäts- und Modellebene werden die Ergebnisse diskutiert, sodass die Schülerinnen und Schüler letztlich das Rutherford’sche Atommodell als tragfähiges Modell benennen. - Anwendungsphase: Modellanwendung, indem die Schülerinnen und Schüler erkennen, dass der Vorgang der Streuung von mehreren Parametern abhängt. So sollten sie im Falle des Luftkissentisch-Modellversuchs zudem beobachtet haben, dass die auftreffenden Magneten auch mit größeren Winkeln gestreut wurden, was auf eine Winkelabhängigkeit der gestreuten α-Teilchen hindeutet. Genauso einsichtig sollte den Schülerinnen und Schülern sein, dass die Streuung von der Feldstärke der Magneten abhängt, was den Kernladungszahlen von einfallendem Teilchen und Folienmaterial entspricht.
Am Ende dieser Überlegungen könnte Gleichung von der Lehrkraft mit dem Hinweis gegeben werden, dass auch Rutherford solche Überlegungen vorgenommen und dieser Gleichung zusammengefasst hat. Solch eine Gleichung ist dann als mathematisches Modell zu verstehen.
Die modellierten Abhängigkeiten können dann mittels der Streukammer überprüft werden, indem die Streurate im Vergleich z.B. von Gold- () und Aluminiumfolie () sowie bei unterschiedlichen Winkeleinstellung des -Strahlers betrachtet wird. - Reflexionsphase: Diskussion und Reflexion der Modellnutzung bzw. des Prozesses der Modellbildung, indem die Schülerinnen und Schüler u.a. die Fragen beantworten, warum ein Modell verwendet wurde und was über die Merkmale des Modells gesagt werden kann.
Den Schülerinnen und Schülern sollte dabei deutlich werden, dass Modelle bewusst für die Beschreibung und Deutung physikalischer Phänomene konstruiert werden und einen hypothetischen Charakter besitzen. So wurden die Atommodelle entwickelt, da z.B. das beobachtete Phänomen der unerwartet geringen Streuung von -Strahlung an einer Metallfolie mit den makroskopisch wahrnehmbaren Eigenschaften der Versuchsbestandteile nicht erklärbar war. Aber auch wenn mit dem Rutherford’schen Atommodell das Streuverhalten erklärt werden kann, so bleibt die „wahre“ Struktur der Metallfolien und der Strahlung doch immer noch (im Rahmen schulischen Unterrichts) nicht direkt wahrnehmbar, sodass das aufgestellte Modell hypothetisch bzw. vorläufig ist, bis ein plausibleres Modell entwickelt wird.
An dieser Stelle müssen auch die Modellgrenzen[15] deutlich gemacht werden, die allerdings sehr gut als Übergang zu einer nächsten Unterrichtseinheit und einem weiteren Modell (Bohr’sches Atommodell) genutzt werden kann.
Versuchsanleitung
Aufbau
Für den Versuchsaufbau[16] werden die folgenden Materialien benötigt:
- (1) 1 Vakuumpumpe (Enddruck: etwa 1 mbar)
- (2) 1 Rutherford-Streukammer mit Halbleiterdetektor und Spaltblende (2mm x 6mm)
- (3) 1 Digitalzähler[17]
- (4) 1 kleiner Stativfuß
- (5) je 1 Gold- und Aluminiumfolie auf Kunststoffplatte mit 12-mm-Kreisöffnung(Foliendicken: Au 2μm, Al 7μm) sowie je zwei Kunststoffplatten mit Kollimatorspalte (1mm und 5mm breit)
- (6) 1 HF-Kabel (1m)
- (7) 1 Netzstecker
- (8) 1 Verbindungskabel 1,50 m, 6-polig
- (9) 1 Messkabel BNC/4-mm-Stecker
- (10) 1 Diskriminator-Vorverstärker
- Americium-241-Präparat
Gemäß dem Titelbild wird zunächst der Diskriminator (10) im Stativfuß (4) befestigt. Anschließend wird dieser mit der Streukammer (2) verbunden,[18] indem das HF-Kabel (6) von der BNC-Buchse der Streukammer (2), von der das Detektorsignal abgeht, zu der Eingangs-Buchse (BNC) des Diskriminators (10) geführt wird. Die Spannungsversorgung des Diskriminators (10) wird mit dem Verbindungskabel (8) sichergestellt, indem es mit der Vielfachbuchse des Diskriminators (10) und der Vielfachbuchse auf der Rückseite des Digitalzählers (3) verbunden wird. Der Digitalzähler (3) ist dann mit dem Netzstecker (7) an eine Netzsteckdose anzuschließen.
Schließlich wird der Diskriminator (10) noch mit dem Digitalzähler (3) über das Messkabel (9) verbunden. Dieses wird in den Diskriminator-Ausgang und den Eingang E (4mm-Buchsen) auf der Vorderseite des Digitalzählers (3) gesteckt. Das Potentiometer des Diskriminators (10) ist auf null einzustellen.
Die Streukammer (2) wird mittels eines Schlauches über den entsprechenden Anschluss mit der Vakuumpumpe (1) verbunden. Am Schlauchanschluss der Streukammer (2) ist auch ein Hahn mit eingebautem Luftfilter angebracht, damit die Kammer behutsam evakuiert und belüftet werden kann.
Um das Americium-241-Präparat und die Folien (5) in die Streukammer (2) einzuspannen, wird der mit der Winkelskala beschriftete Deckel der Kammer umgekehrt auf den Tisch gelegt (Abb. 3). Für Streuversuche im Winkelbereich werden die Halterungen (2.1) und (2.2) benötigt. Die Halterung (2.3) kommt erst bei der Demonstration der Rückstreuung zum Einsatz. Zunächst ist das Americium-241-Präparat in Halterung (2.1) zu befestigen. Anschließend wird ein „Sandwich“ aus Kollimatorspalt (1mm) und z.B. Goldfolie (5) in Halterung (2.2) eingespannt. Dabei soll der Kollimatorspalt in Richtung des Americium-241-Präparats und die Kreisöffnung in Richtung des Halbleiterdetektors zeigen.
Die Spaltblende des Halbleiterdetektors muss nun noch lotrecht ausgerichtet werden, indem die Markierung am Umfang der Blende nach oben zeigt. Dies sollte sehr sorgfältig passieren, da eine nicht lotrechte Ausrichtung der Blende zu einer asymmetrischen Verteilung der Zählraten führen kann. (Gleichung lässt eine spiegelsymmetrische Verteilung der Zählraten erwarten, d.h., bei sollten annähernd die gleichen Zählraten gemessen werden.)
Schließlich wird die Streukammer (2) wieder mit dem Deckel geschlossen und der Schwenkarm (2.3) an den Rand der Kammer bewegt, damit die Messung nicht gestört werden kann.
Soll die Rückstreuung demonstriert werden, bleibt das Americium-241-Präparat in Halterung (2.1) befestigt und wird in die 150° Stellung gebracht. Die Goldfolie (5) z.B. wird ohne Kollimatorspalt in Halterung (2.3) eingespannt. Nach dem Auflegen des Deckels auf die Streukammer (2)soll sich die Goldschicht (nicht die Kreisöffnung) vor dem Americium-241-Präparat und dem Halbleiterdetektor befinden.
Grundsätzlich sind beim Aufbau die unten aufgeführten Sicherheitshinweise im Umgang mit radioaktiven Stoffen zu beachten.
Durchführung
Aufgrund der kurzen Reichweite von -Teilchen in Luft wird die Streukammer (2) mittels der Vakuumpumpe (1) auf einen Enddruck von etwa 1mbar evakuiert. Ist dieser Enddruck erreicht, wird der Hahn am Schlauchanschluss der Streukammer (2) geschlossen und die Vakuumpumpe (1) kann abgeschaltet werden.
Der Digitalzähler (3) wird eingeschaltet und der Eingang E per Knopfdruck ausgewählt. Um die Zählrate angezeigt zu bekommen, muss zudem die Messgröße „COUNTS“ in der oberen linken Ecke des Digitalzählers (3) aktiviert sein. Die Messung wird mit Betätigen der „START/STOP“-Taste in der rechten oberen Ecke des Digitalzählers (3) begonnen und beendet.
Vor der eigentlichen Messung sollte überprüft werden, ob der Halbleiter Signale aufgrund der Umgebungsbeleuchtung liefert. Diese sind nicht erwünscht und können mittels des Diskriminators (10) unterdrückt werden. Dazu wird das Potentiometer des Diskriminators (10) soweit hochgeregelt, bis die Zählrate bei null bleibt. Dabei ist jedoch zu beachten, dass das Potentiometer nicht so hoch eingestellt wird, dass auch Signale der -Teilchen unterdrückt werden. Ggf. ist die Streukammer (2) mit einem Tuch abzudecken.
Zur Messung der Streurate in Abhängigkeit des Streuwinkels wird der Schwenkarm, auf dem sich die Folie (5) und das Americium-241-Präparat befinden, von außen auf eine bestimmte Winkeleinstellung gedreht. Der jeweilige Streuwinkel kann mittels eines Längsschnitts im Schwenkarm von der auf dem Deckel der Streukammer (2) abgedruckten Winkelskala abgelesen werden.
Für Messungen zur quantitativen Auswertung werden die Streuraten z.B. in Schritten von 5°, beginnend bei 0° die Streuraten im Winkelbereich von unter Verwendung des 1mm Kollimatorspaltes aufgenommen. Dafür wird der Streuwinkel nach obigem Vorgehen eingestellt und die Messung durch einmaliges Betätigen der „START/STOP“-Taste des Digitalzählers (3) begonnen. Nach einer zuvor festgelegten Messdauer wird die Messung durch erneutes Drücken der „START/STOP“-Taste unterbrochen und der Wert notiert.
Zur Messung der Streurate in Abhängigkeit des Folienmaterials wird genauso wie oben beschrieben vorgegangen, nur das zuvor das Folienmaterial auszutauschen ist.
Um die Rückstreuung zu messen, ist die Streukammer (2) wie oben beschrieben umzubauen. Nach erneutem Evakuieren der Streukammer (2) wird die Messung durch Betätigen der „START/STOP“-Taste des Digitalzählers (3) begonnen.
Ergebnisse
Bei der Messung der Streurate bei unterschiedlichen Winkeleinstellungen und unter Verwendung von Goldfolie (5) und des 1mm Kollimatorspalts können die Schülerinnen und Schüler sehr eindeutig beobachten, dass die Streurate sehr schnell mit größerem Winkel abnimmt. Die Messzeiten, um eine angemessene Anzahl[19] von Signalen zu detektieren, nehmen mit größeren Winkeln schnell zu (Tab. 1).
Da bereits eine Messdauer von 30 Minuten bei 30° kaum mehr in einer einzelnen Unterrichtsstunde zu vertreten ist, wird empfohlen, Messungen zur quantitativen Auswertung nur im Winkelbereich von durchzuführen. Bei größeren Winkeln lässt sich die Zählrate durch das Verwenden des 5mm Kollimatorspalts erhöhen und damit die Messdauer verringern. Allerdings sind die daraus resultierenden Messwerte dann auf die „1mm-Spalt-Bedingung“ umzurechnen, indem die 5mm-Spalt-Werte mit einem Korrekturfaktor zu multiplizieren sind. Dieser ergibt sich als das Verhältnis der bei dem Winkel gemessenen Streuraten, bei dem der 1mm und 5mm breite Kollimatorspalt verwendet wurde; also der Winkel, bei dem der Wechsel des Kollimatorspaltes stattgefunden hat.[20]
Wird die Goldfolie durch die Aluminiumfolie (5) unter Beibehaltung des 1mm Kollimatorspalts ausgetauscht, können die Schülerinnen und Schüler beobachten, dass die Zählrate bei 0° weit über der Zählrate bei Verwendung der Goldfolie liegt. Hingegen liegen die Streuraten bei Winkeln größer oder kleiner 0° deutlich unter denen, die bei Verwendung der Goldfolie gemessen wurden (Tab. 2).
Wird die Streukammer (2) zur Darstellung der Rückstreuung umgebaut und die Messung gestartet, können die Schülerinnen und Schüler zunächst gar nichts sehen. Auch nach mehreren Minuten wird der Digitalzähler (3) kein Signal detektiert haben. Selbst am Ende einer Unterrichtsstunde werden nur wenige Signale (im unteren einstelligen Bereich) aufgenommen sein.
| θ [°] | Δt [s] | N [Imp] |
|---|---|---|
| -30 | 1860 | 26 |
| -20 | 1200 | 86 |
| -15 | 600 | 126 |
| -10 | 213 | 243 |
| -5 | 150 | 983 |
| 0 | 99 | 1618 |
| 5 | 150 | 1492 |
| 10 | 260 | 512 |
| 15 | 600 | 246 |
| 20 | 1200 | 138 |
| 30 | 1800 | 60 |
| θ [°] | Δt [s] | N [Imp] |
|---|---|---|
| -10 | 213 | 29 |
| -5 | 150 | 1406 |
| 0 | 100 | 2410 |
| 5 | 150 | 316 |
| 10 | 213 | 9 |
| θ [°] | Δt [s] | N [Imp] | |||
|---|---|---|---|---|---|
| -30 | 1860 | 26 | 0,01 | 0,002 | 222,85 |
| -20 | 1200 | 86 | 0,07 | 0,006 | 1099,81 |
| -15 | 600 | 126 | 0,21 | 0,01 | 3445,16 |
| -10 | 213 | 243 | 1,14 | 0,05 | 17330,69 |
| -5 | 150 | 983 | 6,55 | 0,1 | 276236,94 |
| 0 | 99 | 1618 | 16,34 | 0,3 | k.L. |
| 5 | 150 | 1492 | 9,95 | 0,2 | 276236,94 |
| 10 | 260 | 512 | 1,97 | 0,06 | 17330,69 |
| 15 | 600 | 246 | 0,41 | 0,02 | 3445,16 |
| 20 | 1200 | 138 | 0,12 | 0,007 | 1099,81 |
| 30 | 1800 | 60 | 0,03 | 0,003 | 22,85 |
Auswertung
Die sehr geringe Streurate bei einem Winkel von 150° ist allerdings genau die Beobachtung, die die Schülerinnen und Schüler bei der Rückstreuung machen sollen. Schon bei Betrachtung der Winkelabhängigkeit in Gleichung ist zu erwarten, dass bei sehr großen Winkeln die Zählrate extrem klein wird, d.h., die Wahrscheinlichkeit, dass ein Teilchen von einem Goldatomkern zurückgestreut wird, ist extrem gering. Die von den Schülerinnen und Schülern gemachte Beobachtung unterstützt demnach das von Rutherford formulierte Atommodell.
Aufgrund der extrem langen Messzeiten ist diese Einstellung allerdings nicht für eine quantitative Auswertung geeignet und sollte nur zu qualitativen Demonstrationszwecken genutzt werden.
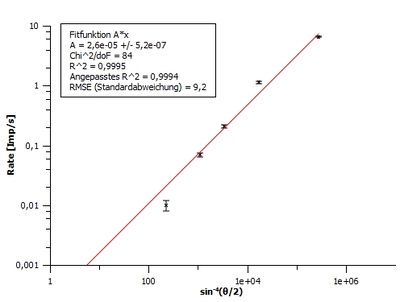
Um die Gültigkeit von Gleichung zu überprüfen, werden die Daten aus Tab. 3 — z.B. mit dem Programm QtiPlot — in einem Diagramm aufgetragen und mit einer Fitfunktion analysiert (Abb. 4). Am einfachsten ist das Verwenden einer linearen Fitfunktion wie in Abb. 4 geschehen. Dabei wird der Faktor als Variable x identifiziert und die übrigen Faktoren als Anstieg A. Dabei ergibt sich die Zählrate aus der Division der Impulse durch die Messdauer. Zusätzlich müssen Abszisse und Ordinate mit Log10 skaliert sein.
Die Einstellung des Winkels an der Streukammer (2) ist sehr präzise möglich, weshalb hier kein Messfehler abgeschätzt wurde. Die Unsicherheit für die Zählrate ergibt sich mittels Gauß’scher Fehlerfortpflanzung wie folgt:
Für die Ablesegenauigkeit von Digitalzähler und Stoppuhr wurden und gewählt.
In Abb. 4 wurden die Werte aus Tab. 3 des positiven Winkelbereichs grafisch verwendet. Aufgrund der Achsensymmetrie der Sinusfunktion ist dies zur Verdeutlichung der Gültigkeit von Gleichung ausreichend. Würden alle Werte mit entsprechender Ausgleichsgerade genutzt, wären zwei parallel verschobene Verteilungen zu sehen.
Wie das Chi^2/doF aus Abb. 4 zeigt, wurde das Fehlerintervall der Zählrate zu gering gewählt. Allerdings sollte der zusätzliche Fehler nicht in der Ablesegenauigkeit der Messinstrumente gesucht werden, sondern vielmehr in Ungenauigkeiten bei der Justierung der Streukammer (2). V. a. die nicht lotrechte Ausrichtung der Spaltblende am Detektor, eine ungenaue Kollimatorspaltjustierung oder die nicht zentrische Verteilung der strahlenden Substanz im Präparathalter sind als systematische Fehlerquellen anzusehen. Diese Fehlerquellen zeichnen sich durch eine Verschiebung der Zählraten längs der Abszisse aus, was anhand der Werte in Tab. 1 und Tab. 2 auch zu sehen ist. In beiden Tabellen sind die Werte innerhalb eines Winkelbereiches größer als in dem entgegengesetzten.
Um die Abhängigkeit der Streurate von der Kernladungszahl der Metallfolie (5) zu überprüfen, können die Streuraten für Gold und Aluminium aus Tab. 1 und 2 für gleiche Winkel ins Verhältnis gesetzt werden. Gemäß Gleichung muss das Verhältnis wie folgt bedingt sein:[21]
Dabei bezeichnet die Atomzahldichte, die sich mit der Dichte und der relativen Atommasse des Folienmaterials ergibt zu:
Mit den Daten für die Aluminiumfolie: , , , und für die Goldfolie: , , , Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle d=2\mathrm {\mu m} } erhält man:
- Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\frac {{\dot {N}}\left(Al\right)}{{\dot {N}}\left(Au\right)}}=0,097}
Nach den Daten aus Tab. 1 und 2 erhält man nur bei für die Aluminiumfolie eine etwa 10mal kleinere Streurate als für die Goldfolie. Die Ursache für die massiven Abweichungen ist wohl in den oben dargestellten systematischen Fehlern zu suchen.
Sicherheitshinweise
- Sorgfalt im Umgang mit radioaktiven Präparaten. Trotz geringer Strahlungsintensität und -reichweite ist das Americium-241-Präparat nicht auf andere Menschen zu richten. Zudem gilt der Strahlenschutzgrundsatz, sich der Strahlung so wenig und kurz wie möglich auszusetzen.
- Metallfolien (5) nicht berühren. Nur am Kunststoffrahmen anfassen.
- Streukammer (2) sehr vorsichtig belüften, da ansonsten Zerstörung der Metallfolien (5) droht. Dazu die Folie parallel zum zu erwartenden Luftstrahl ausrichten.
Anmerkungen
- ↑ http://www.idn.uni-bremen.de/chemiedidaktik/material/Teilchen/teilchen/Atombau/rutherford_streuversuch02.htm# (letzter Zugriff : 03.08.2017, 12:10 Uhr).
- ↑ Handbuch des Physikunterrichts, S. 179.
- ↑ Gröber.
- ↑ Kircher, S. 785-790.
- ↑ Kircher, S. 784.
- ↑ Rahmenlehrplan für die gymnasiale Oberstufe in Berlin und Brandenburg. Physik. 2006, S. 22. Zu finden unter https://www.berlin.de/sen/bildung/unterricht/faecher-rahmenlehrplaene/rahmenlehrplaene/ (letzter Zugriff: 03.08.2017, 12:10 Uhr).
- ↑ Mikelskis-Seifert; Leisner-Bodenthin, S. 15 f.
- ↑ Handbuch des Physikunterrichts, S. 8 f.
- ↑ Mikelskis-Seifert; Leisner-Bodenthin, S. 16.
- ↑ Ebd.
- ↑ Ebd., S. 15 und 19, Nöding, S. 74-76 sowie Handbuch des Physikunterrichts, S. 10.
- ↑ Die folgenden Ausführungen basieren auf Mikelskis-Seifert; Leisner-Bodenthin, S. 20-22 sowie Mikelskis-Seifert, S. 134.
- ↑ U.a. zu finden bei Rhöneck; Niedderer, S. 68-71.
- ↑ Natürlich müsste im Vorfeld geklärt werden, warum ein Magnet geeignet ist, ein Atom bzw. ein α-Teilchen nachzubilden bzw. wo die Grenzen liegen.
- ↑ Für das Rutherford’sche Atommodell hier nachzulesen: https://de.wikipedia.org/wiki/Rutherfordsches_Atommodell#Probleme (letzter Zugriff: 05.08.2017, 14:30 Uhr).
- ↑ Der grundsätzliche Versuchsaufbau und die notwendigen Materialien unter Angabe der Leybold-Didactic-Artikelnummern sind zusätzlich in der Gebrauchsanweisung der Streukammer aufgeführt, www.ld-didactic.de/documents/de-DE/GA/GA/5/559/55956d.pdf (letzter Zugriff: 06.08.2017, 11:05 Uhr).
- ↑ Streukammer-Gebrauchsanweisung hier zu finden: www.ld-didactic.de/documents/de-DE/GA/GA/5/575/57548d.pdf (letzter Zugriff: 06.08.2017, 11:10 Uhr).
- ↑ Auch für die nachfolgenden Verbindungsvorgänge siehe Abb. 2.
- ↑ Aus Gründen der Messgenauigkeit und zur Reduzierung des statistischen Fehlers wird das Detektieren von mind. 10 Teilchen empfohlen. Siehe Streukammer-Gebrauchsanweisung, www.ld-didactic.de/documents/de-DE/GA/GA/5/575/57548d.pdf (letzter Zugriff: 06.08.2017, 11:10 Uhr), S. 3.
- ↑ Handbuch der experimentellen Physik, S. 14.
- ↑ Vgl. Handbuch der experimentellen Physik, S. 14 f.
Literatur
- Gröber, Sebastian (2008): Der Rutherfordsche Streuversuch als RCL, https://www.lehrer-online.de/unterricht/sekundarstufen/naturwissenschaften/physik/unterrichtseinheit/ue/entdeckung-des-atomkerns-rcl-rutherford-streuversuch/ (letzter Zugriff: 05.08.2017, 10:10 Uhr).
- Handbuch der experimentellen Physik. Sekundarstufe II, hrsg. v. Wilfried Kuhn, Köln: Aulis-Verl. Deubner, Bd. 10: Kerne und Teilchen 2, verf. v. Manfred Bormann [u.a.] (2001).
- Handbuch des Physikunterrichts. Sekundarstufe I, hrsg. v. Rainer Götz, Helmut Dahncke u. Fritz Langensiepen, Köln: Aulis-Verl. Deubner, Bd. 8: Atom- und Kernphysik, Astronomie, Technikbezüge, verf. v. Helmut Fischer (1998).
- Kircher, Ernst (2015): Modellbegriff und Modellbildung in der Physikdidaktik, in: Ders.; Girwidz, Raimund; Häußler, Peter (Hrsg.): Physikdidaktik. Theorie und Praxis, 3. Aufl., Berlin Heidelberg: Springer, S. 783-807.
- Mikelskis-Seifert, Silke; Leisner-Bodenthin, Antje (2010): Die Modellmethode, in: Mikelskis-Seifert, Silke; Rabe, Thorid (Hrsg.): Physik Methodik. Handbuch für die Sekundarstufe I und II, Berlin: Cornelsen, S. 15-29.
- Mikelskis-Seifert, Silke (2010): Modellmethode als epistemologisches und didaktisches Konzept, in: Mikelskis, Helmut F. (Hrsg.): Physik Didaktik. Handbuch für die Sekundarstufe I und II, Berlin: Cornelsen, S. 120-138.
- Nöding, Siegfried. (1973): Modelle und Modelldenken im Chemieunterricht – Möglichkeiten und Grenzen, in: Der mathematisch-naturwissenschaftliche Unterricht 26, S. 74-76.
- Rhöneck, Christoph v.; Niedderer, Hans (2010): Schülervorstellungen und ihre Bedeutung beim Physiklernen, in: Mikelskis, Helmut F. (Hrsg.): Physik Didaktik. Handbuch für die Sekundarstufe I und II, Berlin: Cornelsen, S. 52-73.

























![{\displaystyle \mathbf {{\dot {N}}[{\frac {Imp}{s}}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7973e819435b7265dc7436c610526458b6c5dbd9)
![{\displaystyle \mathbf {u_{\dot {N}}[{\frac {Imp}{s}}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f42be7986f8ba738af1c0dfbd6e0b0f2fc93cafe)