Röntgenspektroskopie

Röntgenspektroskopie
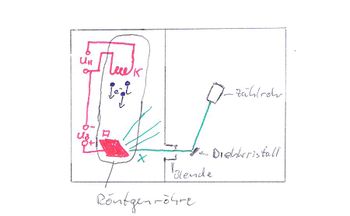
Der Versuchsaufbau in der Gesamtansicht
Kurzbeschreibung
Der Versuchsaufbau zur Röntgenspektroskopie bietet nicht nur die Möglichkeit ein Gesamtspektrum der Röntgenstrahlung aufzunehmen, sondern mit geringen Modifikationen auch einen Einblick in den Aufbau von Kristallen.
Kategorien
Atom- und Kernphysik, Spektroskopie
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	Wechselwirkung, Struktur der Materie
Sonstiges
Durchführungsform	Lehrerdemoexperiment, Schülerdemoexperiment
Anspruch des Aufbaus	leicht
Informationen
Name:	Tobias Kuhnig
Kontakt:	${\text{tobias.kuhnig}}$@${\text{rub.de}}$
Uni:	Ruhr-Universität Bochum
Betreuer*in:	Irene Neumann, Hanno Michel

Experimente mit Röntgenspektrometern sind nicht nur wegen ihres für den Lehrer einfach zu realisierenden Aufbaus und der ohne große Tricks gut reproduzierbaren Ergebnisse für den Einsatz in der Schule gut geeignet, sie bieten zudem die Möglichkeit den Unterrichtsstoff mit in Wissenschaft und Technik genutzten Analyse- und Messmethoden zu verbinden. Diese Analytik ist besonders wichtig, wenn neue Kristallstrukturen, wie zum Beispiel Galliumarsenid (ein wichtiger Grundstoff in der Halbleiter- und Lasertechnik) auf ihren Aufbau oder ihre Qualität untersucht werden sollen. Das Wissen um Aufbau und Qualität eines Kristalls ist unter anderem für den Bau von Lasern, wie sie in Laserpointern vorkommen wichtig.

Didaktischer Teil

Röntgenspektroskopie findet in Wissenschaft und Technik vielfach Anwendung, wodurch sich dieses Thema gut an die Lebenswelt der Schülerinnen und Schüler anknüpfen lässt und für manche auch eine Verbindung zu ihren späteren Berufen darstellt. So sind Röntgenstrahlen den Schülerinnen und Schülern aus dem medizinischen Kontext der Röntgenaufnahme bekannt. Ziel dieses Versuches ist die Aufnahme eines Röntgenspektrums mit den Schülerinnen und Schülern. Um das Thema Röntgenspektroskopie zu verstehen und ihre Phänomene erklären zu können, müssen Schülerinnen und Schüler Energieerhaltung, Austrittsarbeit, Energieniveaus in Atomen, Absorption und Emission von Photonen, Kristallaufbau (von einfachen kubischen Kristallen) Beugung am Gitter sowie natürlich Röntgenstrahlung und ihre Entstehung verstanden haben und miteinander verknüpfen können. Durch geringfügige Modifikationen im Versuchsaufbau können aber auch andere Themengebiete vertieft werden. Setzt man zum Beispiel einen Filter vor die Strahlaustrittsöffnung, so bietet dieser Versuch die Möglichkeit, die Gitterkonstante von Kristallen zu bestimmen. Beispiele für diesen Anwendungsbezug stellen unter anderem Kristalle dar, welche in Lasern wie sie in Laserpointern, CD/DVD/Blueray-Spielern oder medizinischen Geräten eingebaut werden zum Einsatz kommen. Die Absorption von Röntgenstrahlung, wie sie bei Röntgenaufnahmen in der Medizin oder bei der Überprüfung von Schweißnähten angewand wird, lässt sich ebenfalls durch geringe Änderungen im Versuchsaufbau realisieren.

Physikalischer Hintergrund

Röntgenstrahlung

Zur Erzeugung von Röntgenstrahlung werden von einer

Abb. 2: schematische Darstellung des Spektrometers; A = Anode, K = Kathode, U_H = Heitzspannung, U_B = Beschleunigungsspannung, X = Röntgenstrahlung (durch anklicken vergrößerbar)

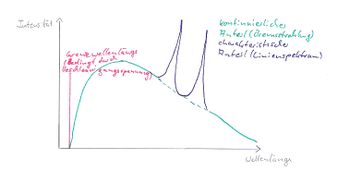
Glühkathode (vgl. Abb. 2) erzeugte freie Elektronen in einem elektrischen Feld durch Hochspannung (einige kV) auf eine Anode beschleunigt. Dort treten zwei Effekte auf. Zum einen werden die Elektronen beim Eintritt in Materie abgebremst. Da es sich damit um beschleunigte Ladungen handelt, strahlen sie Energie in Form von Photonen ab. Hieraus ergibt sich ein kontinuierliches Spektrum

Abb. 3: schematische Darstellung eines Röntgenspektrums (durch anklicken vergrößerbar)

. Dieses ist auf der Seite des Energiemaximums durch die von der Beschleunigungsspannung vorgegebene Energie begrenzt (vgl. Abb. 3), während es zur anderen Seite asymptotisch gegen 0 geht. Zum anderen finden aber auch beim Eindringen der Elektronen in die Anode Stöße zwischen den eindringenden Elektronen und den inneren Elektronen der Metallatome im Anodenmaterial statt, durch welche diese auf höhere Energieniveaus angehoben werden. Wechseln diese angeregten Metallatome nun in den Grundzustand zurück, so senden sie Photonen mit für den jeweiligen Übergang charakteristischen Energien aus. Diese erzeugen dann ein Linienspektrum, welches für das jeweilige Anodenmaterial charakteristisch ist. Überlagert man nun diese beiden Spektren, das kontinuierliche und das charakteristische, so erhält man das in diesem Experiment messbare Gesamtspektrum.

Bragg-Bedingung

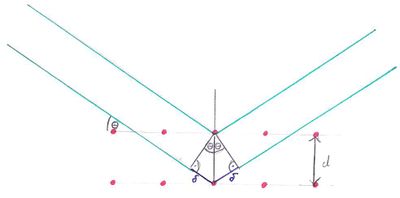
Die Bragg-Bedingung ermöglicht es uns unter Kenntnis entweder des Gitterabstandes d die Wellenlänge $\lambda$ der Röntgenstrahlung zu berechnen oder umgekehrt. Letzteres erfordert allerdings monochromatische Röntgenstrahlung. Die Bragg-Bedingung lässt sich aus wenigen geometrischen Überlegungen und ein wenig Kenntniss der Strahlenoptik ähnlich den Bedingungen für konstruktive Interferenz an Gittern herleiten. Wie in der nebenstehenden Abbildung (Abb. 4)

Abb. 4: Geometrische Veranschaulichung der Bragg-Bedingung (durch anklicken vergrößerbar)

zu erkennen ist muss der Strahl, der in den Kristall eindringt einen um die Strecke $2\delta$ längeren Weg zurücklegen, als der an der Oberfläche reflektierte Strahl. kennt man nun die Gitterkonstante d und den Einstrahlwinkel der Röntgenstrahlung $\theta$ so kann man durch Anwendung einfacher geometrischer Beziehungen zu $2\delta =2d\operatorname {sin} (\theta )$ kommen. Wenn man nun noch die Kenntnis besitzt, dass für konstruktive Interferenz der Gangunterschied $2\delta$ ein ganzzahliges Vielfaches der eingestrahlten Wellenlänge betragen muss, ergibt sich die Bragg-Bedingung zu: $n\lambda =2d\operatorname {sin} (\theta )$

Durch Umstellen dieser Gleichung nach d oder $\lambda$ lässt sich aus dem Winkel des Kristalls zum Strahl und Kenntnis der anderen Variablen das Gesuchte berechnen.

Versuchsanleitung

Aufbau

Benötigte Geräte: Röntgenspektrometer mit Zubehör (Fa. Phywe)(Schlitzblende und Drehkristall (LiF)), Demonstrations-Digitalzähler (Fa. Steinegger), passendes Verbindungskabel (vgl. Abb. 5)

Abb. 5: Beschrifteter Gesamtaufbau (durch anklicken vergrößerbar)

Die Schlitzblende und der Drehkristall werden wie in der Abbildung (Abb. 6) zu sehen ins Spektrometer eingesetzt.

Abb. 6: Schlitzblende und Drehkristall Einbau im Spektrometer (durch anklicken vergrößerbar)

Anschließend werden beide Geräte mit einem Kabel miteinander verbunden und an das Stromnetz angeschlossen.

Durchführung

Nach Einschalten des Digitalzählers wird dieser durch zweimaliges Drücken der Taste bei F (vgl. Abb. 7)

Abb. 7: Bedienfeld Ereigniszähler (durch anklicken vergrößerbar)

auf E/s (Ereignisse pro Sekunde) eingestellt. Über den Schalter C (vgl. Abb. 8)

Abb. 8: Bedienfeld an der Frontseite des Röntgengeräts (durch anklicken vergrößerbar)

wird das Röntgengerät bei geschlossener Frontscheibe eingeschaltet und über den Drehknopf E eine Spannung zwischen 6,9 kV und 25 kV eingestellt (Wert wird im Feld e angezeigt). Die gelbe Warnleuchte bei D zeigt an, dass die Frontscheibe des Versuchsraumes korrekt geschlossen ist und Röntgenstrahlung erzeugt wird. Die beiden Drehknöpfe an der linken Seite des Geräts (vgl. Abb. 9)

Abb. 9: Drehknöpfe zum verstellen von Kristall- und Zählrohrwinkel an der Linken Seite des Röntgengeräts (durch anklicken vergrößerbar)

dienen zur Verstellung des Winkels von Drehkristall (Zeiger a) bzw. Zählrohr b (vgl. Abb. 10)

Abb. 10: Zählrohr mit Zeiger für den Winkel und Zeiger für den Winkel des Drehkristalls (durch anklicken vergrößerbar)

zum Röntgenstrahl.

Zum Beginn der Messreihe wird der Drehkristall mittels Drehknopf A (Abb. 9) auf einen Winkel von 2° eingestellt, da unterhalb dieses Wertes mit zu starken Störeffekten aus dem direkten Strahlverlauf der Röntgenstrahlung zu rechnen ist. Das Zählrohr wird mittels Drehknopf B auf den doppelten Wert des Kristallwinkels eingestellt (wenn die Skalierung des Geräts nicht ganz zuverlässig ist muss man in einem Bereich von ca. 2° um den eigentlichen Zählrohrwinkel nach einem Maximum suchen). Ausgehend von diesen Startwinkeln wird der Kristallwinkel nun in 1°-Schritten erhöht und der Zählrohrwinkel jeweils auf den doppelten Winkel eingestellt (ggf. Suche nach dem Maximum).

Ergebnisse

Für eine Beschleunigungsspannung von U = 19 kV wurden in einer Beispielmessung an einem LiF-Einkristall (d = 2,01 Å) folgende Winkel-Intensitäts-Werte aufgenommen und durch die Bragg-Bedingung in Wellenlängen umgerechnet:

$\theta _{1}$ / ° (Drehkristallwinkel)	$\theta _{2}$ / ° (Zählrohrwinkel)	$\Delta \theta$ / °	$\lambda _{1}$ / pm (aus $\theta _{1}$)	$\lambda _{2}$ / pm (aus $\theta _{2}$)	$\Delta \lambda$ / pm	Zählrate / Ereignisse/s
2	5	0,5	14	18	4	26,5
3	7	0,5	21	25	4	26,4
4	9	0,5	28	32	4	21,1
5	11	0,5	35	39	4	13,9
6	13	0,5	42	46	4	11,5
7	15	0,5	49	52	4	9,4
8	18	0,5	56	63	4	13,3
9	19	0,5	63	66	4	138
10	21	0,5	70	73	4	300
11	23	0,5	77	80	4	367
12	25	0,5	84	87	4	410
13	27	0,5	90	94	4	385
14	29	0,5	97	101	4	352
15	31	0,5	104	107	4	326
16	33	0,5	111	114	4	291
17	35	0,5	118	121	4	250
18	37	0,5	124	128	4	219
19	40	0,5	131	137	4	270
20	41	0,5	137	141	4	583
21	44	0,5	144	151	4	359
22	45	0,5	151	154	4	558
23	45,5	0,5	157	155	4	225
24	49	0,5	164	167	4	87
25	51	0,5	170	173	4	68
26	53	0,5	176	179	4	57
27	55	0,5	183	186	4	43
28	57	0,5	189	192	4	36,5
29	59	0,5	195	198	4	32

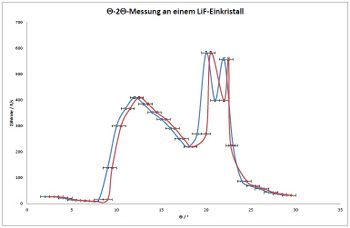
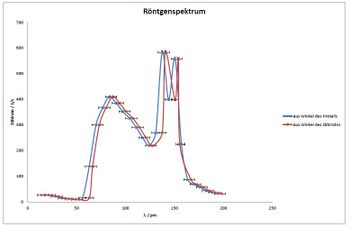
Die Fehler für die Winkel ($\Delta \theta$) und die Wellenlänge ($\Delta \lambda$) sind jeweils für beide Reihen angegeben. Sie ergeben sich aus der Ablesegenauigkeit der Skala und deren Umrechnung in Wellenlängen. Der Fehler der Zählrate wird zu 1% abgeschätzt, dieser Fehler entsteht durch die Totzeit des Zählrohrs. Eine Auftragung der Intensität in Abhängigkeit vom Kristallwinkel (blau) bzw. des halbierten Zählrohrwinkels (rot) ist in Abb. 11

Abb. 11: Winkelabhängigkeit der Intensität (durch anklicken vergrößerbar)

zu sehen.

Auswertung

Da bei dem vorliegenden Gerät die Maxima der Röntgenstrahlung nicht bei den doppelten Werten des Winkels des Drehkristalls zu finden waren, wurden nicht nur die Winkel des Drehkristalls sondern auch die halbierten Zählrohrwinkel zur Auswertung herangezogen. Diese Abweichungen in den Winkeln könnten eventuell auf nicht mehr ganz gerade Zeiger zurückzuführen sein. Mit der Bragg-Bedingung lassen sich die Winkel in Wellenlängen umrechnen (vgl. Abb. 12)

Abb. 12: Wellenlängenabhängiges Spektrum (durch anklicken vergrößerbar)

. Man kann deutlich den Verlauf (vgl. auch schematische Darstellung in Abb. 3) des Röntgen-Bremsspektrums erkennen, der Anteil des Linienspektrums ist auf Grund der großen Winkelsprünge nur qualitativ gut zu erkennen. Vergleicht man die Wellenlänge der zweiten Linie des aus den Zählrohrwinkeln gewonnenen Spektrums ((154 ± 4) pm) mit der Wellenlänge für die Cu-K_α Linie (157 pm), so stellt man eine gute Übereinstimmung fest. Auch die Cu-K_β-Linie aus dem Spektrum ((141 ± 4) pm) passt gut zum Literaturwert von 139 pm. Betrachtet man das Spektrum, welches aus den Winkeln des Drehkristalls gewonnen wurde, so lassen sich die beiden Linien zu (151 ± 4) pm (Cu-K_α) bzw. (137 ± 4) pm (Cu-K_β) bestimmen. Die Literaturwerte liegen auch hier im Fehlerbereich der gemessenen Linien, aber die aus dem Zählrohrwinkel bestimmten Werte passen insgesamt besser überein.

Sicherheitshinweise

Es ist zu beachten, dass Schülerinnen und Schüler von 16 bis 18 Jahren am Betrieb von Schulröntgeneinrichtungen nur unter Aufsicht mitwirken dürfen. Zudem müssen die Geräte der Röntgenverordnung entsprechen.