Quantitative Bestimmung der Hall-Spannung

Quantitative Bestimmung der Hall-Spannung
Abb. 1: Hall-Effekt-Gerät mit Silberplättchen der Firma LEYBOLD-HERAEUS
Kurzbeschreibung
Das beschriebene Experiment dient der quantitativen Untersuchung der Hall-Spannung und wird an einem Silberplättchen durchgeführt. Ziel ist die teilweise Herleitung der Hall-Spannung.
Kategorien
Elektrizitätslehre
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	System und Wechselwirkung
Sonstiges
Durchführungsform	Demoexperiment
Anzahl Experimente in dieser Unterkategorie	1
Anspruch des Aufbaus	schwer
Informationen
Name:	Franziska Vaihinger
Kontakt:	${\text{vaihinger}}$@${\text{physik.hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Tobias Ludwig

Befindet sich ein stromdurchflossener Leiter in einem Magnetfeld, so werden die Ladungsträger, aufgrund der Lorentzkraft senkrecht zur Stromrichtung abgelenkt. Durch diese Auslenkung kommt es an den seitlichen Begrenzungen des Leiters zu einer Potentialdifferenz, welche als Hall-Spannung messbar ist (vgl. Könneker, C. und Reichert, U.). Dieses Phänomen wurde nach Edwin Hall benannt und wird in elektrischen Bauteilen, wie zum Beispiel der Hall-Sonde, welche unter anderem in Smartphones verbaut sind, genutzt.

Didaktischer Teil

In diesem Abschnitt wird das reale Experiment zur Untersuchung der Hall-Spannung einem Simulationsexperiment gegenübergestellt. Dabei wird auf beobachtbare Aspekte und Phänomene in beiden Fällen eingegangen. Für die Gegenüberstellung wurde eine Arbeitsumgebung von GeoGebra verwendet, welche auf der Webseite von GeoGebra als Download erhältlich ist.

In der Arbeitsumgebung der Simulation können die verschiedenen Größen variiert und die Hall-Spannung für jede Einstellung abgelesen werden. Dabei liefern aufgenommene Messreihen, analog zu den in dem Kapitel Durchführung beschriebenen, proportionale Zusammenhänge bei den untersuchten Größen. Diese Simulation soll jedoch vor allem das Verständnis des Hall-Effekts fördern, da diese auf einer Modellebene arbeitet. So werde in dem angedeuteten Silberplättchen Ladungsträger als kleine blaue Punkte dargestellt, welche sich vom angelegtem Minus-Pol zum Plus-Pol des Querstroms bewegen. Bei Anlegen eines Magnetfeldes suggeriert die Anordnung der Ladungsträgern an den Seiten, an denen die Hall-Spannung gemessen wird, dass Ballungsgebiete entstehen würden. Auch wenn dieses physikalisch nicht vertretbar ist, so wird jedoch bei dieser Darstellung deutlich, dass jedes abgelenkte Elektron einen Elektronenmangel an der gegenüberliegenden Seite erzeugt. Dadurch wird Schülerinnen und Schüler (SuS) bewusst, dass die negativ geladene Seite des Silberplättchens durch einen Überschuss an Elektronen und die positiv geladene Seite durch einen Mangel an Elektronen erzeugt wird.
Schwierigkeiten könnten zudem durch dieses Modell bei SuS auftreten, da Elektronen verschiedene Färbungen besitzen. Das suggeriert, dass es sich bei diesen Teilchen um verschiedene Arten handelt, was physikalisch gesehen nicht der Fall ist.
Zudem befindet sich in dieser programmierten Simulation ein Punkt ($A_{0}$) in der Mitte des Silberplättchens. Dieser könnte durch die modellhafte Darstellung der Elektronen als blaue Punkte mit solchen verwechselt werden. Dieser ist jedoch lediglich der Fixpunkt der Abbildung und könnte mit wenigen Änderungen nicht angezeigt werden.

Bei der Durchführung und Auswertung des realen Experiments hingegen befindet sich die experimentierende Person über die gesamte Zeit in einer realen Umgebung und beobachtet nicht berechnete, aber gemessene Werte. Dabei wird ein großer Störfaktor deutlich. Die Kontakte der Kabel, welche die Hall-Spannung messen, sind produktionsbedingt nicht korrekt auf einer Äquipotentiallinie an dem Silberplättchen angebracht. Ein Nachjustieren ist daher notwendig. Dies führt bei der Untersuchung der Querstrom-Abhängigkeit dazu, dass zwar ein linearer, aber kein proportionaler Zusammenhang messbar ist. Dadurch kann das auftretende Phänomen nicht im Ganzen beobachtet werden. Jedoch bietet sich die Möglichkeit über Ursachen, Fehlerquellen und Störgrößen zu diskutieren.

Abschließend lässt sich zusammenfassen, dass bei dem realen Experiment nicht alle Einflussgrößen der Hall-Spannung untersucht werden können und zum Teil die physikalischen Zusammenhänge nicht messbar sind. Dafür tritt der Hall-Effekt real auf, sodass eine Hall-Spannung gemessen werden kann. Bei dem Simulationsexperiment ist dies zwar möglich, wobei sich jedoch die Frage stellt warum SuS diese Zusammenhänge untersuchen sollen, wenn die Formel zur Berechnung der Hall-Spannung schon gegeben ist. Ist dies nicht gewünscht, müsste eine Modifikation der Arbeitsumgebung durchgeführt werden. Zudem arbeitet das hier ausgewählte Simulationsexperiment auf einer Modellebene, welche zum Teil Fehlvorstellungen der SuS bekräftigt und Elementarteilchen beobachtbar macht.

Versuchsanleitung

Dieser Versuch wurde auf Grundlage der Experimentieranleitung der Firma LEYBOLD-HERAEUS aufgebaut und durchgeführt.

Aufbau

Bei diesem Versuch wurde folgendes Material verwendet:

Abb. 2: Versuchsaufbau zur quantitativen Bestimmung der Hall-Spannung

Abb. 3: Skizze des Versuchsaufbaus zur quantitativen Bestimmung der Hall-Spannung. Erstellt mit www.draw.io

Abb. 4: Hall-Effekt-Gerät mit beschrifteten Buchsen

• Analog-Demo-Amparemeter (PHYWE) Messbereich bis 10 A
  • nach Gebrauchsanweisung auch möglich: Analog-Demo-Amparemeter (LEYBOLD Nr. 531911)
• Multimeter (PeakTech Modell: 2010 DMM)
• 2 Stelltrafo (PHYWE Nr. 13532-93)
• Mobile-CASSY 2 (LEYBOLD Nr. 524005)
• Mikrovoltmeter (LEYBOLD Nr. 53213)
• Teslameter (LEYBOLD Nr. 51662)
• Tangentiale B-Sonde (LEYBOLD Nr. 51660)
• 2 Spulen (PHYWE Nr. 06513.01) $~300~Wdg.,~max.~4~A,~0,8~\Omega ,~2~mH\,$
• Eisenkern in U-Form
• 2 Spulenschuhe
• Hall-Effekt-Gerät (Silber) (LEYBOLD Nr. 586 81, Gebrauchsanweisung)
• Verbindungskabel
• Stative und Stativfüße
• Laborhelfer

Der Versuchsaufbau besteht aus drei separaten Stromkreisen (in Abb. 2 und Abb. 3 farbig (gelb, rot, blau) gekennzeichnet). Dabei bildet der erste Stromkreis (rot) eine Reihenschaltung vom ersten Stelltrafo, dem Analog-Demo-Amparemeter und dem Hall-Effekt-Gerät. Bei dem Hall-Effekt-Gerät werden die Buchsen (siehe Abb. 4: B1 und B2) für den Querstrom genutzt. Der zweite Stromkreis (blau) besteht ebenfalls aus einer Reihenschaltung des zweiten Stelltrafos, dem Multimeter, dem Mobile-CASSY und den beiden Spulen. Um die auftretende Hall-Spannung messen zu können, wird im dritten Stromkreis der Mikrovoltmeter (Input) an die Buchsen (B2 und B3) des Hall-Effekt-Geräts angeschlossen. Der zweite Eingang des Mobile-CASSYs wird mit dem Output des Mikrovoltmeters verbunden. Zum Schluss wird das Teslameter mit der Tangentialen B-Sonde verbunden und diese mit Hilfe von Stativmaterial so nah wie möglich an das Silberplätchen des Hall-Effekt-Gerätes geführt. Hierbei ist darauf zu achten, dass die verwendete tangentialen B-Sonde mit der breiteren Seite misst.

Durchführung

Der erste Teil des Versuches besteht darin eine $I_{B}$-$B$-Kalibrierungskurve aufzunehmen. Dies dient dazu Messwerte einer eindeutigen magnetischen Flussdichte zuzuordnen. Dabei ist darauf zu achten, dass vor der Aufnahme der Kalibrierungskurve der Elektromagnet entmagnetisiert ist. Hierfür genügt es kurzzeitig $5~A~$~ durch die Spule fließen zu lassen. Nach dem Entmagnetisieren wird die magnetische Flussdichte $B$ in Abhängigkeit des Magnetstromes $I_{B}$ gemessen. Hierfür wird der Magnetstrom in Schritten von $0,5~A$ erhöht und die magnetische Flussdichte an dem Teslameter abgelesen.

Der zweite Teil besteht aus der Aufnahme einer $B$-$U_{H}$-Kurve. Dafür wird bei konstantem Querstrom $I_{Q}$ (hier wurden $10~A$ verwendet) die magnetische Flussdichte schrittweise erhöht und die mit dem Multivoltmeter gemessenen Hall-Spannungen abgelesen. Dies kann auch über eine Messung mit Hilfe des Mobile-Cassy passieren. Hierfür muss vor der schrittweisen Erhöhung der magnetischen Flussdichte das Mobile-CASSY gestartet werden. Die aufgenommenen Daten können anschließend aus dem Mobile-CASSY zur Weiterverwendung ausgespeist werden. In diesem Teil des Versuches ist darauf zu achten, dass vor der Messung eine Kalibrierung der Kontakte am Silberplättchen vorzunehmen ist. Hierfür wird bei einem konstantem Querstrom und keinem äußerem Magnetfeld die Schraube oberhalb der Buchsen so lange verstellt, bis keine Hall-Spannung messbar ist.

Der dritte Teil des Versuches ist analog zum zweiten Teil durchzuführen. Dabei wird jedoch eine $I_{Q}$-$U_{H}$-Kurve bei konstantem Magnetsrom (hier wurden $4~A$ verwendet) aufgenommen. Da eine Kalibrierung der Kontakte am Silberplättchen durchzuführen ist, ist es nicht möglich eine Messung für keinem Querstrom ($I_{Q}=0$) anzustellen.

Ergebnisse

Alle folgenden Ergebnisse wurden wie im Kapitel Durchführung beschrieben aufgenommen. Zuerst wurde die Messung für die $I_{B}$-$B$-Kalibrierungskurve durchgeführt. Die Messwerte werden in Tabelle 1 dargestellt.

Tabelle 1:Aufgenommene Messwerte für die $I_{B}$-$B$-Kalibrierungskurve

Magnetstrom $I_{B}$	magnetische Flussdichte $B$
0	0
1	2
1,5	5
2	8
2,5	10
3	12
3,5	15
4	16
4,5	19
5	21
5,5	23
6	24

Anschließend wurde der Zusammenhang zwischen dem magnetischen Fluss und der Hall-Spannung untersucht. Die Durchführung des zweiten Teiles des Versuchs lieferte die in Tabelle 2 angeführten Messwerte.

Tabelle 2: Messwerte der Hall-Spannung $U_{H}$ bei ansteigendem magnetischen Fluss $B$

magnetischer Fluss $B$	Hall-Spannung $U_{H}$
0	0,03
2	0,05
5	0,08
8	0,12
10	0,13
12	0,16
15	0,19
16	0,22
19	0,25
21	0,28
23	0,30
24	0,32

Abschließend wurde die Auswirkung eines steigenden Querstromes auf die Hall-Spannung betrachtet. Die hierfür aufgenommenen Messwerte sind in Tabelle 3 zu finden.

Tabelle 3: Messwerte der Hall-Spannung $U_{H}$ bei ansteigendem Querstrom $I_{Q}$

Querstrom $I_{Q}$	Hall-Spannung $U_{H}$
0	-0,20
1	-0,17
2	-0,13
3	-0,08
4	-0,05
5	-0,04
6	0,00
7	0,02
8	0,06
9	0,10
10	0,14

Auswertung

Um den Zusammenhang der untersuchten Größen zu der Hall-Spannung interpretieren zu können, ist es notwendig die aufgenommenen Messwerte innerhalb ihrer Unsicherheiten zu betrachten. Hierfür wurden bei den Messwerten die Herstellerangaben betrachtet.
Die Unsicherheit des Magnetstromes beträgt $6\%$ des Messwertes, der Fehler des magnetischen Flusses berechnet sich aus $1\%$ des Messwertes $+1~mT$ und der Fehler der gemessenen Hall-Spannung beträgt $0,01~V$. Zudem musste bei den aufgenommenen Messwerten der Hall-Spannung einen Offset-Korrektur vollzogen werden, da es beim Experimentieren nicht möglich war die Kontakte am Silberplättchen korrekt zu kallibrieren. Diese betrug bei der Bestimmung der Hall-Spannung in Abhängigkeit des magnetischen Flusses $-0,03~U$ und bei der Bestimmung der Hall-Spannung in Abhängigkeit des Querstromes $+0,04~V$. Diese Rechnungen wurden mit einem Tabellenkalkulationsprogramm durchgeführt und können hier einzeln nachvollzogen werden.
Durch diese Betrachtungen lassen sich die Ergebnisse graphisch mit Hilfe des Programmes Qtiplot darstellen. Außerdem wurde eine Ausgleichsgerade durch die Messpunkte gelegt, um den Zusammenhang der jeweiligen Messgrößen zu verdeutlichen.

Abb. 5: Proportionaler Zusammenhang der magnetischen Flussdichte und der gemessenen Hall-Spannung

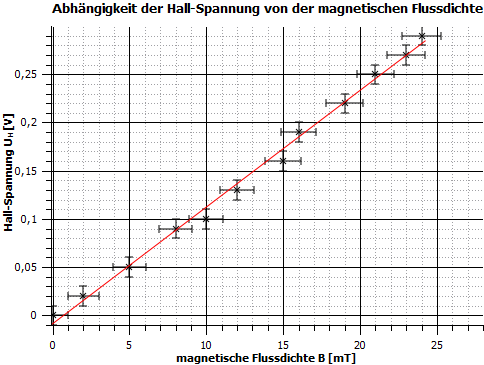
Die in rot in Abbildung 5 eingefügte Fit-Funktion ist eine Lineare Funktion ($f(x)=a\cdot x+b$) mit den Parametern $a=0,0121\pm 0,0003$ und $b=-0,009\pm 0,004$. Somit ergibt sich, innerhalb der Messunsicherheiten, ein proportionaler Zusammenhang zwischen der magnetischen Flussdichte und der Hall-Spannung. Das heißt es gilt $U_{H}\propto B$.

Abb. 6: Linearer Zusammenhang des Querstroms und der Hall-Spannung

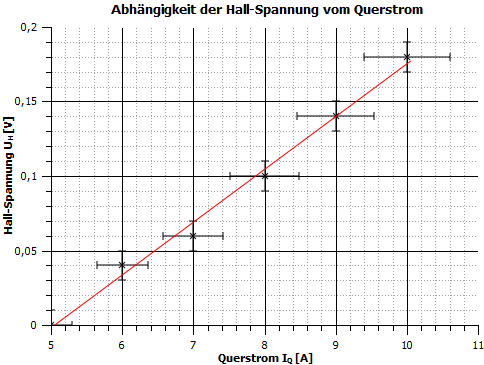
In dem $I_{Q}$-$U_{H}$-Diagramm (Abb. 6) ist ein linearer Zusammenhang erkennbar. Auch hier wurde eine Lineare Funktion als Fit durch die Messpunkte gelegt. Diese hat die Parameter $a=0,035\pm 0,002$ und $b=-0,18\pm 0,01$. Da die Ausgleichsgerade, innerhalb der Messunsicherheit, nicht durch den Ursprung verläuft kann an dieser Stelle nicht von einem proportionalem Zusammenhang gesprochen werden. Dies lässt sich auf die Durchführung des Experimentes zurückführen. Da die Kontakte an dem Silberplättchen bei einem konstantem Querstrom kalibriert werden müssen, ist ein Nulldurchgang nicht möglich. Es wurde nach der Kalibrierung bei $5~A$ Messwerte bis $10~A$, welche dargestellt worden sind und Messwerte bis $0~A$ aufgenommen, welche auf Grund des negativen Vorzeichens aus den Betrachtungen ausgeschlossen werden. Ein negatives Vorzeichen würde eine gegengerichtete Spanung bedeuten, welche auf Grund des Versuchaufbaus nicht möglich ist, da weder der Querstrom noch der magnetische Fluss während der Aufnahme der Messwerte umgepolt wurden. Somit gilt der Zusammenhang $U_{H}=a\cdot I_{Q}+b$ zwischen dem Querstrom und der Hall-Spannung.

Somit kann zusammenfassend die Formel der Hall-Spannung $U_{H}={\frac {B\cdot I_{Q}}{n\cdot e\cdot d}}$ nicht vollsändig hergeleitet bzw. überprüft werden. Das durchgeführte Experiment bestätigt zum einen einen proportionalen Zusammenhang zwischen der Hall-Spannung und der magnetischen Flussdichte, konnte jedoch zum anderen aufbaubedingt nur einen linearen Zusammenhang zwischen der Hall-Spannung und dem Querstrom aufzeigen. Weiterführend wäre es interessant die Dicke des Silberplättchens zu variieren oder den beschriebenen Versuch mit anderen Plättchen zu wiederholen und zu vergleichen, um die Hall-Konstante $R_{H}$ einzuführen.

Sicherheitshinweise

Für die Durchführung des beschriebenen Experiments ist vorher die Experimentieranleitung der Firma LEYBOLD-HERAEUS zu lesen. Es ist darauf zu achten, dass Stromkreise bei einem Querstrom über $15~A$ bzw. bei einer Magnetstromstärke über $5~A$ nur kurzzeitig eingeschalten werden, da sonst eine Erwärmung der Experimentierkabel bzw. eine Überslastung der Spulen hervorgerufen werden kann (vgl. Leybold Didactic GmbH , S.2). Allgemein wird bei der Durchführung mit einer maximalen Spannung von $10~A$ gearbeitet, weshalb eine gesundheitliche Gefährdung auszuschließen ist.

Siehe auch

• Cam,Y. und Oden, N.: Hall-Effekt