Lissajous-Figuren aus Sand
| Lissajous-Figuren aus Sand | |
 Spur einer von fünf Einstellungen des Lissajous-Pendels | |
| Kurzbeschreibung | |
|---|---|
| Mit diesem Pendel können Lissajous-Figuren mechanisch erzeugt werden. | |
| Kategorien | |
| Mechanik, Elektrizitätslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | System |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Rebecca Drutschmann |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
Lissajous-Figuren entstehen durch die Überlagerung zweier zueinander senkrechter Schwingungen mit unterschiedlichen Frequenzen f, wenn das Verhältnis eine rationale Zahl ist (Demtröder[1] (2006), S. 360). Das hier vorgestellte Pendel kann über seine gesamte Länge nur in eine Richtung schwingen und über einen Teil seiner Länge, , zusätzlich eine dazu senkrechte Schwingung durchführen. Über den Zusammenhang der für quasimathematische Pendel angenommen werden kann, gilt . Es ist also möglich, gewünschte Frequenzverhältnisse über Längeneinstellungen am Pendel zu erreichen. Auslaufender Sand legt die Spur der so entstehenden Bahnkurven – Lissajous-Figuren können abgebildet werden.
Inhaltsverzeichnis
Didaktischer Teil: Elementarisierung nach Bleichroth
Die mathematische Beschreibung von Lissajous-Figuren ist komplex (vgl. z.B. Demtröder[1] (2006), S.360 oder Meschede[2] (2006), S. 142). Eine Möglichkeit zur Aufbereitung komplexer Inhalte bietet die Elementarisierung nach Bleichroth[3] (1991). Sie sei hier verstanden als ein Prozess der didaktischen Aufbereitung eines Gegenstandes, der drei Aspekte umfasst: die Vereinfachung, die Bestimmung des Elementaren und die Zerlegung des Lernvorgangs in Elemente (ebd., S.4f.).
Elementarisierung im Sinne von Vereinfachung (erster Aspekt) verlange, so der Autor, „die Abstraktheit eines Inhalts zu vermindern und seine Komplexität abzubauen“, sodass er der „altersstufengemäße[n] geistige[n] Entwicklung, d[er] geistige[n] Leistungsfähigkeit und d[er] Lernvorgeschichte der Schülergruppe“ angemessen dargeboten werden könne (Bleichroth[3] (1991), S.6). Es werden Einzelfälle anstelle allgemeiner Sätze und die Beziehungen von Einzelelementen anstelle eines Gesamtzusammenhangs betrachtet (ebd.).
Zur Bestimmung des Elementaren als zweiter Aspekt der Elementarisierung werde die „grundlegende[...] Idee, d[as] Grundprinzip[...] oder de[r] erschließende[...] Kerngedanke[...] freigelegt. Dieses Elementare sollen die Schüler an einem Inhalt erfassen und verstehen“ (ebd., S.4). Ausgehend von Musterbeispielen gelangen Schülerinnen und Schüler durch Generalisierung zum Verständnis einer allgemeinen Gesetzmäßigkeit (ebd., S. 9).
Der dritte Aspekt der Elementarisierung als Zerlegung in methodische Elemente soll nach Bleichroth „eine schrittweise Erfassung und Aneignung des Inhaltes möglich machen“ (ebd.). Gemeint ist damit v.a. die überlegte Ausrichtung einer Unterrichtsreihe auf ein sukzessive zu erschließendes Erkenntnisziel (ebd., S.10). Aber auch einzelne Teilschritte (wie hier ein Experiment) müssen wiederum zweckmäßig zergliedert werden.
Die vorgestellten drei Aspekte der Elementarisierung werden beispielsweise bei der didaktischen Überlegungen zum Thema Wärmeübertragung relevant, wie in einem Vortrag im Sommersemester 2017 geschehen (vgl. dazu den entsprechenden Artikel): Im Sinne der Vereinfachung werden alle Prozesse mit dem Teilchenmodell erklärt, es werden, wie es der zweite Aspekt verlangt, die drei unterschiedlichen, grundlegenden Prinzipien Wärmeleitung, Konvektion und Wärmestrahlung identifiziert, wobei diese Zergliederung nach Prinzipien gemäß dem dritten Aspekt auch einer methodischen Zerlegung entspricht.
In der Konzeption des hier vorgestellten Pendelversuchs waren ebenfalls Überlegungen aller drei Aspekte der Elementarisierung nach Bleichroth leitend: Der physikalische Gegenstand, der behandelt werden soll, sind die Lissajous-Figuren. Vereinfachend werden hier lediglich zwei Figuren als repräsentative Einzelfälle untersucht. Anstatt die Entstehung der Figuren als komplexes Zusammenwirken von Phasendifferenz, Frequenzverhältnis und Verzerrung durch unterschiedliche Amplituden verstehen zu wollen, werden die interessierenden Zusammenhänge auf die Auswirkung der Frequenzverhältnisse beschränkt. Verglichen mit der Erzeugung der Figuren am Oszilloskop kann hier auch insofern von einer Reduktion der Abstraktheit gesprochen werden, als dass ihr Zustandekommen (als Prozess) den Schülerinnen und Schülern offen vor Augen geführt wird: Die Figuren sind als Spur einer mechanischen Pendelbewegung erkennbar.
Das Elementare als die zugrunde liegende physikalische Gesetzmäßigkeit ist die Überlagerung von Schwingungen verschiedener Richtungen. Zudem sollte von der Zielgruppe auf basaler Ebene verstanden werden, wie Lissajous-Figuren entstehen:
Die Bewegung des schwingenden Objekts in der Zeit kann als Bahnkurve aufgezeichnet werden. Diese Kurve gibt die Auslenkung in die eine Richtung (y) in Abhängigkeit von der Auslenkung in die andere Richtung (x) an. Wenn es eine Periode T gibt, nach der n Schwingungen in x-Richtung und m Schwingungen in y-Richtung vollständig durchgeführt wurden, entstehen geschlossene Figuren. Denn das schwingende Objekt befindet sich nun wieder in seiner Ausgangssituation (gleicher Ort, gleiche Energien). Es wird also wieder die gleiche Bewegung in T vollziehen.
Die Zergliederung des Vorgehens in methodische Elemente wird aus der Durchführung ersichtlich: Die Bewegung des Pendelkörpers als Überlagerung von Schwingungen in zwei Richtungen wird vom Publikum beobachtet, anschließend das Zustandekommen der Spur verfolgt und exemplarisch für fünf Frequenzverhältnisse verglichen. Diese Teilschritte sollen Schülerinnen und Schülern allmählich zur Erkenntnis der zugrunde liegenden Prinzipien verhelfen.
Versuchsanleitung
Ein erster Vorschlag für diesen Versuch wurde der Sammlung „Physikalische Freihandexperimente“ (Hilscher[4] (2012), S.221-224) entnommen. Weitere Anregungen entstammen dem Video „Sand pendulums – Lissajous patterns“ von Bruce Yeany (s. [1]). Der Aufbau wurde um eigene Überlegungen ergänzt und an die örtlichen Gegebenheiten angepasst.
Aufbau
Material
- 2 Haken, in der Decke verankert
- 1 leere PET-Flasche (0,5l)
- ca. 8m feste, unelastische Schnur, z.B. Paketband
- 1 Karabiner
- ca. 2l Sand
- 4 Stahlkugeln (m=0,064kg)
- 1 dunkles Stofftuch (ca. 1,5m x1,5m)
- 1 Rolle Malerkreppband
Werkzeug
- Cutter
- Ahle
- Maßband (mindestens 4m)
- Taschenrechner
Anleitung zum Aufbau
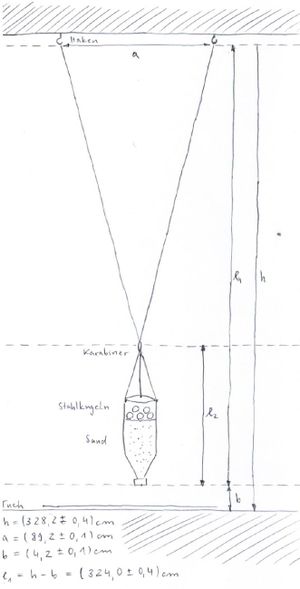
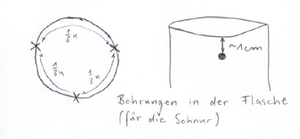
Eine Skizze des Aufbaus mit sämtlichen Maßen findet sich nebenstehend (s. Abb. 3). Die Haken müssen in einem geeigneten Abstand in der Decke befestigt sein. Von der PET-Flasche wird der Boden mit dem Cutter entfernt. Ca. 1cm unter der Schnittkante werden mit der Ahle drei Löcher gebohrt (s. Abb. 4), um die Flasche daran gerade aufhängen zu können.
Durch jedes Loch wird ein Schnurstück gezogen ( je ca. 20cm) und mit einem Knoten befestigt. An ihren Enden werden alle drei Schnüre zusammengeknotet, sodass bei gerade hängender Flasche alle Schnüre gespannt sind. Der Deckel der Flasche wird abgeschraubt, erhält ebenfalls ein Loch (ca. 0,5cm Durchmesser) und wird wieder aufgedreht. Die Schnittränder müssen sauber sein, damit der Sand gut ausfließen kann.
Nun wird ein Stück Schnur benötigt, das ca. doppelt so lang ist wie der Abstand von den Haken in der Decke bis zum Boden. Am einen Ende wird eine Schlinge geknotet, die über einen der Haken gelegt wird. Mit dem Karabiner wird die Aufhängung der Flasche in die lange Schnur gehängt. Mit einer zweiten Schlinge wird die lange Schnur so am zweiten Deckenhaken eingehängt, dass der Flaschendeckel mit dem Loch sich wenige Zentimeter über dem Boden befindet. Um die Elastizität der Schnur zu berücksichtigen, können die 4 Stahlkugeln dabei bereits in der Flasche liegen. Unter der Flasche wird das schwarze Tuch ausgebreitet und das Loch im Flaschendeckel mit etwas Malerkrepp verklebt, bevor Sand eingefüllt wird. Die Stahlkugeln müssen auf dem Sand liegen, um das Loch nicht zu verschließen. Sie dienen der Optimierung der Massenverhältnisse zwischen Aufhängung und schwingendem Körper, sodass auch bei geringem Sandfüllstand idealisierend ein mathematisches Pendel angenommen werden kann.
Die Länge des Pendels muss aus der Höhe der Haken h und dem Abstand des Flaschendeckels vom Boden b errechnet werden. Die gewünschten Längen , mithilfe derer die Einstellung der Frequenzverhältnisse erfolgt, sollten im Vorhinein bestimmt, abgemessen und markiert werden. Durch Zusammenkleben der langen Schnur kann das Pendel von dieser Höhe an bis zum Austrittsloch auch senkrecht zur ersten erlaubten Richtung schwingen. Günstig ist, zunächst alle Verklebungen bis zur maximalen anzubringen und dann in der Durchführung nach und nach aufzureißen. So wird während des Experimentierens nicht allzu viel Zeit für den Umbau benötigt. Für den hier realisierten Aufbau sind sie unten tabellarisch, mit den entsprechenden Frequenzverhältnissen, aufgeführt. Nach welchen Kriterien die verschiedenen ausgewählt wurden, ist in der Auswertung ausgeführt.
Durchführung
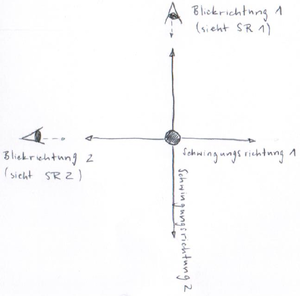
Zunächst wird das Loch im Flaschendeckel verschlossen gehalten. Das Pendel wird diagonal so ausgelenkt, dass alle Schnüre gespannt bleiben, und anschließend losgelassen. Das Publikum wird aufgefordert, sich so zu positionieren, dass es frontal auf den Aufbau schaut, und die Bewegung des Pendels zu beobachten. Anschließend ändert das Publikum seine Position um 90° relativ zum Aufbau und wird wiederum zur sorgfältigen Beobachtung aufgefordert (s. Abb. 5). Die Funktionsweise des Aufbaus sollte an dieser Stelle anhand der Beobachtungen gemeinsam reflektiert werden.
Nun wird der Klebestreifen gelöst, das Loch mit einem Finger verschlossen, das Pendel ausgelenkt und der Sand ausfließen lassen. Nach maximal fünf Schwingungen sollte die Experimentatorin das Pendel stoppen. Die Energieverluste des Systems verwischen sonst das (gewünschte) Ergebnis.
Das Vorgehen wird für fünf verschiedene wiederholt. Die Ergebnisse sind unten tabellarisch zusammengefasst.
Ebenfalls aufgeführt sind dort die jeweiligen Periodendauern in beide Schwingungsrichtungen. Deren Erfassung bietet sich jedoch erst dann an, wenn gemeinsam mit den Schülerinnen und Schülern der Zusammenhang zwischen den Längen und den Frequenzverhältnissen geklärt wurde und diese in Beziehung zu den entstehenden Mustern gesetzt wurden. Aus ökonomischen Gesichtspunkten ist es naheliegend, die Periodendauern vor dem Betrachten der Sandspuren zu messen, aus didaktischer Sicht ist ein umgekehrtes Vorgehen einleuchtender.
Ergebnisse
Die Längen wurden mit einem Maßband abgenommen, die Unsicherheit entspricht einer Skaleneinheit. Da die Messung der Höhe h (s. Abb. 3) einigermaßen fehlerbehaftet ist, wurden hier sechs Werte aufgenommen. Der minimale Wert muss dem wahren Wert (als kürzester Verbindung zwischen Haken und Boden) am nächsten kommen. Für die Unsicherheit wurde die Standardabweichung aus den sechs Werten bestimmt. Die Periodendauern ergeben sich aus der Zeit für zehn Schwingungen, die je sechsmal aufgenommen wurde. Mittelwert und Standardabweichung führen zu den aufgelisteten Ergebnissen und ihren Unsicherheiten. Die Frequenzverhältnisse wurden einmal aus den Längen und ein weiteres Mal aus den Periodendauern errechnet.
| Spur | [cm] | [s] | [s] | |||
|---|---|---|---|---|---|---|
 |
||||||
 |
||||||
 |
||||||
 |
||||||
 |
Auswertung
Aus einer beliebigen Perspektive beschreibt das Pendel für ein unvoreingenommenes Publikum zunächst eine Bewegung, die auf den ersten Blick nicht leicht zu klären ist. Werden jedoch Positionen mit einer Blickachse senkrecht zu je einer Schwingungsrichtung eingenommen, können diese optisch einigermaßen isoliert werden. Die Zuschauerinnen und Zuschauer erkennen: Das Pendel schwingt gleichzeitig in zwei zueinander senkrechten Ebenen. Aus der Überlagerung resultiert die Gesamtbewegung des Pendels. In diesem ersten Schritt soll Schülerinnen und Schülern ein kognitiver Zugang zur Funktionsweise des Aufbaus ermöglicht werden.
In der Reihe fünf verschiedener sollten zwei Lissajous-Figuren vorkommen: Und zwar für die erste vorgeführte Einstellung, um den Schülerinnen und Schülern das Phänomen aufzuzeigen, ihr Interesse zu wecken und einen Anlass zur weiteren Untersuchung zu schaffen. Die zwei weiteren wurden so gewählt, dass keine Figur entsteht. Das Publikum erkennt: Nicht jede Einstellung erzeugt eine Figur. Stattdessen scheint der Sandstrahl alllmählich ein Rechteck auszufüllen (das allerdings aufgrund von Energieverlusten des Pendelsystems immer kleiner wird). Die zweite Lissajous-Figur zeigt auf, dass verschiedene Muster möglich sind und regt zum Nachdenken über ihre Entstehensbedingungen an. Dass anschließend ein weiterer Wert für gewählt wurde, der keine Lissajous-Figur entstehen lässt, weist die Zuschauerinnen und Zuschauer auf die Unabgeschlossenheit der Datenerfassung hin: Weitere Längenverhältnisse bleiben abzuschreiten, weitere Figuren bleiben zu entdecken.
Tatsächlich sind die Muster, die der Sandstrahl erzeugt, zufriedenstellend: Für näherungsweise rationale Frequenzverhältnisse ergeben sich Figuren, die an eine Brezel und an ein Alpha (oder einen Fisch) erinnern. Für alle irrationalen Verhältnisse ändert der schwingende Körper ständig seine Bahn und füllt damit nach und nach das Rechteck zwischen den beiden Amplituden aus. Allerdings erscheint es ungeschickt, aus Messwerten mit begrenzter Genauigkeit diesen Zusammenhang herstellen zu wollen. Einleuchtender ist, das Experiment als Ausgangspunkt für theoriegeleitete Überlegungen zu nutzen, unter welchen Bedingungen geschlossene Figuren entstehen können. Auch die gemessenen Zeiten, wiewohl im Rahmen ihrer Unsicherheit die errechneten Frequenzverhältnisse bestätigend, sollten aus didaktischer Perspektive nicht überbewertet werden. Sie werden geeigneterweise lediglich zur Überprüfung der Annahme herangezogen, dass ist. Und können bei Zeitnot gänzlich ausgespart werden.
Eine Elementarisierung des physikalischen Gegenstands „Lissajous-Figuren“ im Sinne Bleichroths gelingt m.E. anhand des vorgestellten Aufbaus ausgesprochen gut. Wie es der dritte Aspekt der Elementarisierung fordert, muss der Versuch seinerseits in eine methodisch sinnvolle Reihe eingegliedert werden: Wie oben bereits angedeutet, sind anschließende theoretische Überlegungen unerlässlich. Auch eine weitere systematisch-experimentelle Erschließung des Phänomens anhand elektromagnetischer Schwingungen und mithilfe eines Oszilloskops ist denkbar.
Literatur
- ↑ 1,0 1,1 Demtröder, W. (2006): Experimentalphysik I. Mechanik und Wärme. 4. Auflage. Berlin/ Heidelberg
- ↑ Meschede, D. (2006): Gerthsen Physik. 23. Auflage. Berlin/ Heidelberg/ New York
- ↑ 3,0 3,1 Bleichroth, W. (1991): Elementarisierung, das Kernstück der Unterrichtsvorbereitung, in: Naturwissenschaften im Unterricht. Physik. Jg. 2, Nr. 1, S. 4-11
- ↑ Hilscher, H. u.a. (2012): Physikalische Freihandexperimente. Band 1. Mechanik. 4. Auflage. Hallbergmoos
Siehe auch
- Yeany, B. "Sand pendulums - Lissajous patterns - part one // Homemade Science with Bruce Yeany"; https://www.youtube.com/watch?v=uPbzhxYTioM. [18.08.2017]