Kondensator
| Kondensator | |
 Bildunterschrift des Experiments | |
| Kurzbeschreibung | |
|---|---|
| Bestimmung der Ladungsmenge in Abhängigkeit der Spannung eines Plattenkondensators bzw. Bestimmung der Ladungsmenge in Abhängigkeit des Abstands der Platten des Plattenkondensators | |
| Kategorien | |
| Elektrizitätslehre, [[:Kategorie:|Kategorie:]] | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 10 |
| Basiskonzept: | Energie |
| Sonstiges | |
| Durchführungsform | Lehrerexperiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Plocke |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Gromadecki |
Der Kondensator ist eines der wichtigsten elektrischen Bauelemente unserer heutigen Technik. Er wird in vielen Geräten der heutigen Zeit eingebaut und benutzt. Beispiele dafür sind Fernseher, Radio und Fotoapparat, aber auch Teilchenbeschleuniger, wie der Ringbeschleuniger in Cern (Schweiz), wo mit Hilfe von Kondensatoren die Fokussierung von geladen Teilchen gesteuert wird. Mit einem Kondensator können elektrische Ladungen gespeichert werden. Dadurch ist es dem Kondensator möglich elektrische Energie innerhalb seines elektrischen Feldes zu speichern. Mit Hilfe der beiden im Artikel beschrieben Teilversuche sollen fundamentale Eigenschaften des Plattenkondensators, wie zum Beispiel die Kapazität, untersucht werden.
Inhaltsverzeichnis
Didaktischer Teil
Schüler, die mit Kondensatoren vertraut gemacht werden sollen, brauchen Kenntnisse über Grundlagen der Elektrostatik. Sie sollten die Vorgänge im einfachen Stromkreis kennen und mit den Größen Ladung, Stromstärke und Spannung vertraut sein, nach Möglichkeit auch mit Wechselstrom und Wechselspannungen. Im Einzeln sind die folgenden Vorkenntnisse wünschenswert (vgl. Götz[1] (1996), S. 169):
- Trennen von Ladungen
- Nachweis unterschiedlicher Ladungen
- Elementarladung
- Formelzeichen und Einheit der elektrischen Ladung
- Kräfte zwischen Ladungen
- Die elektrische Stromstärke (Erklärung, Formelzeichen und Einheit)
- Die elektrische Spannung (Erklärung, Formelzeichen und Einheit)
- Wechselspannung und Wechselstrom
Gleichzeitig benötigen die Schüler Kenntnisse über das Auswerten von physikalischen Messwerten. Hierzu gehören Kenntnisse aus der Mathematik:
- Proportionalität
- Antiproportionalität
- grafische Darstellungen
Im Folgenden soll nun erläutert werden, wie der Erkenntnisgewinn auf Basis des didaktischen Prinzips der Selbstständigkeit erfolgen kann. Das Prinzip der Selbstständigkeit beinhaltet die Entwicklung des selbstständigen Erarbeitens von neuen Erkenntnissen durch Planen, Ausführen, Kontrollieren von Aktivitäten. (vgl. Weigand[2] (2001), S. 11)[20.09.2016] .
Eine Möglichkeit bei der Vorgehensweise ist es, dass der Lehrer in einem Demonstrationsexperiment gemeinsam mit den Schülern die Messwerte aufnimmt. Die Messwerte könnten an der Tafel dargestellt oder durch Eintragung in eine Excel-Tabelle aufgenommen werden. Dadurch wird gewährleistet, dass die Schüler sinnvolle Messwerte zur Auswertung zur Verfügung haben. Ein Schülerexperiment ist nach den "Richtlinien zur Sicherheit im Unterricht" (GUV-SI 8070) hier nicht möglich, weil zu hohe Spannungen benötigt werden. Durch Quotientenbildung oder eine Diskussion des Kurvenverlaufs stellen die Schüler fest, dass der Quotient aus Ladung und Spannung konstant ist. An der Stelle hat der Lehrer die Möglichkeit den Quotienten aus Ladung und Spannung als Kapazität eines Kondensators zu definieren. Durch die Einführung des Begriffs Kapazität wird die bisher lediglich qualitative Beschreibung des Kondensators durch eine quantitative Aussage ergänzt. Der gewählte methodische Weg bietet weiterhin die Möglichkeit, die Schüler mit der Arbeitsweise zur Gewinnung physikalischer Erkenntnisse vertraut zu machen. Bei der Untersuchung des Zusammenhangs von Ladung und Abstand des Plattenkondensators ist die methodische Vorgehensweise ähnlich. Bei der Auswertung des Kurvenverlaufs können die Schüler eine Antiproportionalität vermuten, sodass sie ein weiteres Diagramm anfertigen müssen. Hierzu müssen sie den Kehrwert vom Abstand bilden und ein Ladung-Reziproker-Abstands-Diagramm erstellen. Daraus lässt sich dann eindeutig die Antiproportionalität von Ladung und Abstand begründen. Am Ende der jeweiligen Experimente sollte der Lehrer mit den Schülern eine Analyse der auftretenden Fehler (Messfehler, Gerätefehler) durchführen, um Ungenauigkeiten, besonders bei den Diagrammen, zu begründen.
Versuchsanleitung
Aufbau
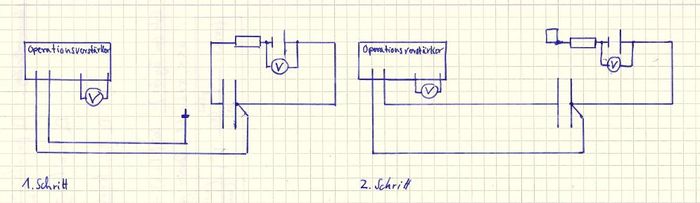
Der Versuch wird nach dem Schaltplan (siehe Abbildung "Schaltplan" Schritt 1) aufgebaut. Für den Versuch werden folgende Geräte gebraucht:
- Plattenkondensator (Artikelnummer Leybold:54422)
- Hochspannungsquelle (Artikelnummer Leybold:52165)
- Operationsverstärker (Artikelnummer Leybold:53200)
- 1x Widerstand 100 Megaohmen
- 2x Spannungsmessgeräte (Voltmeter)
- 1x Coaxialkabel BNC/4mm (Verbindungskabel mit Stecker) (Artikelnummer: 500421)
- 4x Paar Verbindungskabel (verschiedene Längen)
Durchführung
- Teilversuch: Der Abstand des Plattenkondensators wird auf 2 mm eingestellt. Die Spannung an der Spannungsquelle wird auf 50 V eingestellt. Beim Operationsverstärker wird der Verstärkungsfaktor für die Ladung auf 10^(-8) As eingestellt. Der Kondensator wird geladen. Achtung: Dabei ist das Kabel mit dem Stecker, welches vom Operationsverstärker kommt nicht mit dem Kondensator verbunden (siehe Abbildung "Schaltplan" Schritt 1). Der Operationsverstärker wird auf Null gesetzt durch das Drücken des roten Knopfs am Operationsverstärker. Das Kabel zwischen Widerstand und Kondensator wird getrennt und beim Widerstand in sich selber gesteckt, um den Kondensator vom Ladungsstromkreis zu trennen. Das Kabel mit dem Stecker, welches mit dem Operationsverstärker verbunden ist, wird nun mit dem Plattenkondensator verbunden (siehe Abbildung "Schaltplan" Schritt 2). Anschließend wird am Spannungsmessgerät, welches mit dem Operationsverstärker verbunden ist, die Spannung abgelesen und notiert. Danach wird der Plattenkondensator vom Operationsverstärker wieder getrennt und der Widerstand mit dem Plattenkondensator verbunden, damit dieser sich neu Aufladen kann. Die Prozedur wird für 100 V, 150 V, 200 V, 250 V und 300 V wiederholt und die komplette Messserie wird für 4 mm und 6 mm Plattenabstand wiederholt.
- Teilversuch: Durchführung wie beim ersten Teilversuch, allerdings werden nur 100 V eingestellt und der Abstand des Plattenkondensators kontinuierlich in 2 mm Schritten bis etwa 20 mm verändert.
Ergebnisse
1. Bestimmung der Ladung in Abhängigkeit der Spannung bei einem Plattenabstand von 2 mm
| U in V | U in V (Verstärker bei 10 hoch minus 8) | Ladung in As |
|---|---|---|
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (100\pm 1)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (150\pm 1)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (3,70\pm 0,01)} | |
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (6,33\pm 0,01)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (7,48\pm 0,01)} |
2. Bestimmung der Ladung in Abhängigkeit der Spannung bei einem Plattenabstand von 4 mm
| U in V | U in V (Verstärker bei 10 hoch minus 8) | Ladung in As |
|---|---|---|
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,70\pm 0,01)*10^{-8}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (1,35\pm 0,01)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (150\pm 1)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (2,03\pm 0,01)} | |
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (2,61\pm 0,01)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (4,00\pm 0,01)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (4,00\pm 0,01)*10^{-8}} |
3. Bestimmung der Ladung in Abhängigkeit der Spannung bei einem Plattenabstand von 6 mm
| U in V | U in V (Verstärker bei 10 hoch minus 8) | Ladung in As |
|---|---|---|
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,53\pm 0,01)*10^{-8}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (150\pm 1)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (1,47\pm 0,01)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (1,47\pm 0,01)*10^{-8}} |
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (1,90\pm 0,01)} | ||
4. Bestimmung der Ladung in Abhängigkeit des Plattenabstands des Kondensators bei 100 V (Spannungsquelle)
| Abstand in mm | U in V (Verstärker bei 10 hoch minus 8) | Ladung in As |
|---|---|---|
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (2,49\pm 0,01)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (1,40\pm 0,01)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (8\pm 1)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,68\pm 0,01)*10^{-8}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (12\pm 1)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,60\pm 0,01)*10^{-8}} | |
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,54\pm 0,01)*10^{-8}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,50\pm 0,01)*10^{-8}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (18\pm 1)} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (20\pm 1)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (0,45\pm 0,01)} |
Auswertung
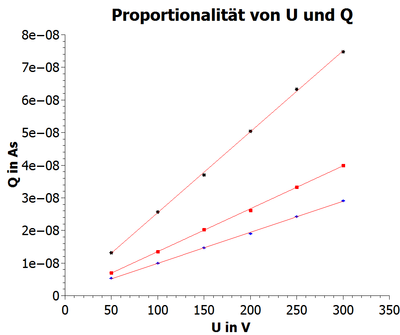
Abbildung 1 zeigt graphisch den proportionalen Zusammenhang von Spannung und Ladung bei drei verschieden Abständen des Plattenkondensators. Zur Berechnung der Ladung wurde die gemessene Spannung am Operationsverstärker mit dem voreingestellten Verstärkungsfaktor 10^(-8) multipliziert. Der Fehler der Spannung ergibt sich jeweils aus dem Ablesefehler der Geräte. Somit ist der Fehler für die Spannung 1 V und für die Ladung 10^(-10) As. Die folgende Tabelle zeigt nochmal rechnerisch den Quotienten von Ladung und Spannung für die drei Abstände, welcher jeweils etwa Konstant ist. Der Quotient ist physikalisch gesehen die Kapazität des Kondensators. Der Fehler für die Kapazität ergibt sich aus der Fehlerfortpflanzung [Delta(C)=(1/U)*Delta(Q)+(Q/(U*U)*Delta(U)]. Zum Vergleich nach Versuch P3.1.7.3 von der Firma LD Didactic GmbH, welche den gleichen Messaufbau verwendet, sowie den gleichen Plattenkondensator, beträgt die Kapazität C = 244 pF bei d = 2 mm, C = 133 pF bei d = 4 mm und C = 92 pF bei d = 6 mm (siehe [1] LD Didactic GmbH). Siehe auch:
- LD Didactic GmbH: P3.1.7.3;
http://www.ld-didactic.de/literatur/hb/e/p3/p3173_e.pdf [20.8.2016]
| Spannung in V | Kapazität (Quotient) in As/V bei 2 mm Abstand | Kapazität (Quotient) in As/V bei 4 mm Abstand | Kapazität (Quotient) in As/V bei 6 mm Abstand |
|---|---|---|---|
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (2,57\pm 0,04)*10^{-10}} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (9,9\pm 0,2)*10^{-11}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (150\pm 1)} | Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (9,8\pm 0,1)*10^{-11}} | ||
| Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (1,30\pm 0,01)*10^{-10}} | |||
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (2,53\pm0,01)*10^{-10}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1,33\pm0,01)*10^{-10}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (9,72\pm0,08)*10^{-11}} | |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (300\pm1)} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (2,49\pm0,01)*10^{-10} } | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1,33\pm0,01)*10^{-10}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (9,70\pm0,07)*10^{-11}} |
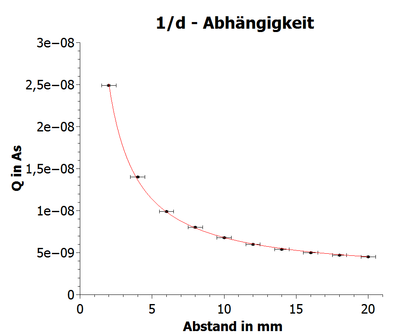
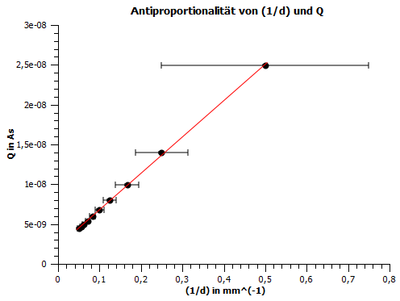
Abbildung 2 zeigt graphisch den Zusammenhang von Abstand des Plattenkondensators und der Ladung bei 100 V Spannung an der Spannungsquelle. Zur Berechnung der Ladung wurde die gemessene Spannung am Operationsverstärker mit dem voreingestellten Verstärkungsfaktor 10^(-8) multipliziert. Der Fehler für den Abstand ergibt sich aus dem Ablesefehler. Somit ist der Fehler für den Abstand 1 mm und für die Ladung 10^(-10) As. Abbildung 3 zeigt die Antiproportionalität von (1/Abstand des Plattenkondensators = d) und der Ladung bei 100 V Spannung an der Spannungsquelle. Der Fehler für (1/d) ergibt sich doch Fehlerfortpflanzung [Delta(1/d)=1/(d*d)*Delta(d)]. Der Fehler für die Ladung ist 10^(-10) As, welcher sich aus dem Ablesefehler ergibt.
Für beide Teilversuche gilt, dass die größten Messunsicherheiten aus zusätzlichen Kapazitäten beim Versuchsaufbau, sowie durch eine vergrößerte Fläche des inhomogenen elektrischen Feldes am Rand der Platten resultieren. Beide Teilversuche bestätigen den proportionalen bzw. antiproportionalen Zusammenhang von Spannung und Ladung bzw. 1/Plattenabstand und Ladung eines Plattenkondensators (vgl.
Thomsen[3]
(1998), S. 102). Die gemessene Werte der Kapazität bei verschiedenen Plattenabständen und die von der Firma LD Didactic GmbH stammenden Werte stimmen sehr gut überein.
Das Fazit beider Versuche ist, dass durch einen einfachen Aufbau grundlegende Eigenschaften eines Plattenkondensators für Schüler hergeleitet werden können.
Abschließend noch eine Bemerkung zur Fehlerberechnung. Für beide Versuche wurden die Fehler mit Hilfe der allgemein gültigen Fehlerfortpflanzung berechnet. Dies ist für die Schüler nicht möglich, da ihnen das Wissen zur Berechnung der Fehlerfortpflanzung fehlt und sie noch nicht vertraut sind mit der Quotientenregel der Differenzialrechnung (erst 11. Klasse). Deswegen sollte mit den Schülern nur eine qualitative Fehlerbetrachtung erfolgen, zum Beispiel in Form einer Diskussion möglicher Fehler beim Versuchsaufbau oder aber das Bilden des arithmetischen Mittels bei der Kapazität.
Sicherheitshinweise
Die Gefahr des Elektrisierens an nicht entladenen Kondensatoren: Sowohl im Demonstrationsexperiment (Vorbildcharakter!) als auch im Schülerexperiment müssen Kondensatoren mit größeren Kapazitäten am Ende des Experiments entladen werden. Bei großen Kapazitäten ist ein entsprechender Widerstand bereitzustellen, um den Entladestrom klein zu halten. Bei großen Entladeströmen können die inneren Zuleitungen und deren Anschlüsse an die Platten des Kondensators schmelzen. Zur Aufbewahrung sollten sie kurzgeschlossen werden, weil sich unter Ladung entstandene Veränderungen nur langsam zurückbilden und dabei erneut Spannung aufgebaut wird; Berührungsgefahr! (siehe Götz [1] (1996), S. 170)
Literatur
- ↑ 1,0 1,1 Götz,R (1996):Handbuch des Physik-Unterrichts Sekundarstufe 1 - Band 6: Elektrizitätslehre II/Elektronik;Aulis Verlag Deubner & Co KG; Köln
- ↑ Weigand,H.-G. (2001): Didaktische Prinzipien;http://www.didaktik.mathematik.uni-wuerzburg.de/fileadmin/10040500/dokumente/Texte_zu_Grundfragen/weigand_didaktische_prinzipien.pdf
- ↑ Thomsen,C (1998): Ein Jahr für die Physik; Wissenschaft und Technik Verlag; Berlin