Kapazität eines Plattenkondensators

Kapazität eines Plattenkondensators
Der Versuchsaufbau
Kurzbeschreibung
Es wird der Einfluß des Plattenabstandes auf die Kapazität eines Plattenkondensators untersucht.
Kategorien
Elektrizitätslehre
Einordnung in den Lehrplan
Geeignet für:	Sek. I und II
Basiskonzept:	Wechselwirkung
Sonstiges
Durchführungsform	Lehrerdemoexperiment
Anspruch des Aufbaus	mittel
Informationen
Name:	Valeri Melev
Kontakt:	${\text{melevval}}$@${\text{physik.hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Stephan Pfeiler

Die Kapazität eines Plattenkondensator ohne Dielektrikum lässt sich mit folgender Formel bestimmen:

$C=\varepsilon _{0}\cdot {\frac {A}{d}}$,

wobei $\varepsilon _{0}$ die elektrische Feldkonstante, $A$ die Fläche einer Platte und $d$ der Plattenabstand sind.

In diesem Experiment geht es in erster Linie um die Nachprüfung der ${\frac {1}{d}}$ - Abhängigkeit der Kapazität. Dabei wurde der Plattenkondensator der Firma Leybold (544 22) verwendet. Bei diesem Gerät lässt sich der Plattenabstand mittels einer Schraube millimetergenau einstellen.

Methodisch hat wird auch der Umgang mit sehr kleinen Ladungen und die Benutzung eines Messverstärkers geübt.

Didaktischer Teil

Die Einführung des Kondensators als einem der wichtigsten Bauteile eines Stromkreises setzt bereits ein grundlegendes Verständnis des Phänomens Elektrizität voraus. Konzepte wie elektrische Ladung, positive und negative Ladung, Kräfte zwischen Ladungen, elektrische Stromstärke und elektrische Spannung, elektrischer Leiter und Isolator und elektrischer Stromfluss müssen verinnerlicht sein. Als didaktisches Ziel sollte das Verständnis der Rolle des Kondensators in einem Stromkreis und seiner Eigenschaften (hier vor allem der Kapazität als charakteristischer Größe) im Vordergrund stehen. Besondere Erwähnung sollte auch der sichere Umgang mit Kondensatoren finden.

Man kann den Kondensator bereits in der Sekundarstufe I einführen und dabei zum Beispiel seine Rolle beim Speichern der Ladung beim Elektronenblitzgerät in den Vordergrund stellen. Man kann sich so erst einmal auf den Fall des Gleichstroms beschränken und das Gelernte dann wieder bei der Behandlung des Wechselstroms in die Erinnerung rufen. So würde also der Lade- und Entladevorgang und die Kapazität den Schwerpunkt des Unterrichts bilden. Man kann experimentell zeigen, dass beim Kondensator Spannung und aufgenommene Ladung zu einander proportional sind und dass also $C=Q\cdot U$ eine stromkreisunabhängige Bauteileigenschaft darstellt.

Hier würde das vorliegende Experiment anknüpfen, in dem es darum geht, zu untersuchen wie Bauteileigenschaften (hier Plattenabstand) sich auf das Verhalten im Stromkreis (hier Kapazität) auswirken. Der Vorteil der Wahl dieses Experiments liegt darin, den mathematischen Zusammenhang nicht als gegeben hinnehmen zu müssen, sondern sich diesen aus experimentell gewonnenen Daten selbst zu erarbeiten.

Weiterhin ist zu erwähnen, dass der verwendete Kondensator (s. Abb. 1) sich von seinem Aufbau her sehr gut als ein Modellkondensator eignet. Man sieht bei ihm die Platten und die Anschlüsse, die zu diesen führen, man kann die Modellvorstellung einer auf die Platten fließenden Ladung sehr gut nachvollziehen, was bei den praktisch nutzbaren Kondensatoren nicht der Fall ist.

Abb. 1: Verwendeter Kondensator

Wichtige Gefahrenhinweise sind weiter unten zu finden.

Versuchsanleitung

Die Versuchsanleitung ist grundsätzlich [1], dem Begleitmaterial des Kondensators, entnommen. Der Versuch besteht aus zwei Teilen: zunächst wird der Kondensator mit Hilfe einer Spannungsquelle, die auf 300V eingestellt ist, über einen 100MΩ-Widerstand aufgeladen. Im zweiten Schritt entlädt man dann den Kondensator über einen Gleichstrommeßverstärker

Vorbereitungen/Grundsätzliches zu E-Statik-Versuchen

Wie häufig bei Versuchen in der Elektrostatik ist auch hier eine sorgfältige Vorbereitung des verwendeten Materials Voraussetzung, um zufriedenstellende Messergebnisse zu erhalten (vgl. auch Götz/Dahnke/Langensiepen (1992), S. 118-119 und [2] Leybold):

• Alle verwendeten Materialien sollten möglichst staubfrei sein, um eine Spitzenwirkung durch diesen zu vermeiden.
• Alle isolierenden Teile, insbesondere die Isolierstiele, auf denen die geladenen Kugeln befestigt sind, sollten nicht nur wegen des Staubs vorab gereinigt werden. So führen z.B. Salze (Schweiß) zu "Leckströmen" bzw. einem Ladungsabfluss von den Kugeln. Dies wollen wir verhindern. Dazu eignet sich besonders destilliertes Wasser oder Spiritus. Bei der Verwendung von Spiritus sollte gerade bei Klebestellen geprüft werden, ob der Kleber nicht angelöst wird. Als Alternative hat sich auch Glasreiniger bewährt.
• Vor der Durchführung sollten die Geräte frühzeitig in den Unterrichtsraum gebracht werden. Ist der Vorbereitungsraum kühler, so bildet sich auf den nun kühleren Geräten ein Feuchtigkeitsfilm. Auch hier kommt es durch Oberflächenströme zu Ladungsabfluss.
• Es ist auch sinnvoll, die Luftfeuchtigkeit im Raum möglichst gering zu halten. Auch wenn diese entgegen der weitverbreiteten Meinung nur eine sekundäre Bedeutung zu haben scheint (vgl. Kastner/Farwig (1983), S. 214-216), verstärkt sie doch obigen Effekt. Dies kann einerseits durch Lüften erreicht werden, andererseits sollten empfindliche Versuche zu Beginn der Stunde durchgeführt werden, da die hohe Anzahl von Schülern/Zuhörern die Luftfeuchtigkeit sehr schnell ansteigen lässt.
• Alle leitenden Teile sollten so weit wie möglich von den geladenen Kugeln entfernt aufgebaut werden, um Influenzeffekte zu minimieren.

Materialien

Abb. 2: Versuchsauufbau

Folgende Materialien sind notwendig

• genügend großer Plattenkondensator mit präzis zu verstellendem Plattenabstand (z.B. der hier verwendete Leybold [3] 544 22)
• Gleichstrom-Meßverstärker (z.B. Leybold 532 00 oder der hier verwendete Phywe 07539.93)
• Spannungsquelle 0-500V
• 2x Multimeter
• 100MΩ-Widerstand + Steckplatte
• 8 Stromkabel
• 1 Erdungskabel

Aufbau

Der Aufbau des Versuchs beginnt zunächst mit dem Stromkreis zur Ladung des Kondensators.

In Abb. 2

In Abb. 1 sieht man den vollständigen, beschrifteten Aufbau des Versuchs. Die Grundlage ist ein Experimentierset von Leybold. Dort finden sich auch weitere Hinweise zu einem Teil der verwendeten Materialien (siehe [4], Leybold, Versuch P3.1.2.2) und zu Teilen des Aufbaus (siehe [5], Handblatt Leybold, Versuch P3.1.2.2, ohne Verwendung des x-y-Schreibers).

Wir beginnen mit dem Aufbau der Messschiene und des Rollwagens. Auf dem Rollwagen muss nun eine der Kugeln mit dem Isolierstiel befestigt werden. Bei Verwendung des Rollwagens, der in Abb. 1 zu sehen ist, ist dies durch Aufstecken möglich, da der Rollwagen einen Kupplungsstecker zum Aufstecken des von innen hohlen Isolierstiels besitzt. Die zweite Kugel wird an dem Kraftsensor befestigt. Dieser wird nun mittels Stativmaterial auf Höhe der ersten Kugel positioniert. Für eine gute Übersicht hat es sich bewährt, keine einzelnen Stative, sondern eine optische Achse zu verwenden (siehe Abb. 1). Da wir die Kugeln zur Messung gleichnamig laden werden, ist es sinnvoll den Kraftmesser so zu drehen, dass abstoßende Kräfte positiv gemessen werden. Die Richtungen sind in der Regel auf dem Kraftsensor markiert. Ein Klemmreiter bzw. Stopper wird nun auf der Messschiene so befestigt, dass die Kugeln sich nicht berühren können. Wird zum Beispiel ein minimaler Abstand von 0,2 cm eingestellt, so ist der Abstand der Kugelmittelpunkte bei $r_{0}=4\ cm$ (Kugeldurchmesser 38 mm, Leybold Ladungskörpersatz). Da auch die Abstandsmessung über den x-y-Schreiber realisiert wird, müssen wir dabei nicht auf die Skala der Messschiene achten. Werden andere Kugeln verwendet, muss jeweils der Kugeldurchmesser bzw. der Abstand der Kugelmittelpunkte bestimmt werden. Der Kraftsensor wird nun noch mit dem Newtonmeter verbunden.

Nun kann das Hochspannungsnetzteil aufgebaut werden. Wir verbinden das Hochspannungskabel mit dem Pluspol und den Minuspol mit Erde bzw. Masse des Netzteils. Die Spitze des Hochspannungskabels wird durch das oberste Loch der isolierten Stativlochstange gesteckt. Das Hochspannungskabel sollte so geführt werden, dass es genügend Abstand zum sonstigen Versuchsaufbau hat, um Influenzeffekte zu minimieren. Dies gilt auch für das Netzteil selbst. Zudem sollte das Kabel den Tisch nicht berühren, da es auf Grund der hohen Spannung zu Überschlägen kommt. Realisiert wurde dies, indem das Kabel über einen Isolator gehängt wurde. Der Isolator wurde mittels Stativstange auf der optischen Achse befestigt (siehe auch dazu Abb. 1). Zur besseren Übersicht können Newtonmeter und Netzteil jeweils auf optische Bänke gestellt werden.

Nun muss noch die Messwerterfassung mittels x-y-Schreiber aufgebaut werden. Der x-y-Schreiber wird wie in Abb. 1 positioniert. Der Ausgang des Newtonmeters wird mit den Experimentierkabeln mit dem y-Eingang des x-y-Schreibers verbunden.
Würden wir nun eine Messung mit dem x-y-Schreiber starten, so zeichnet dieser die Größe der Coulombkraft als y-Wert über eine Zeit t auf, indem sich der Messschlitten in x-Richtung bewegt. Diese Funktion nutzen wir aus, um die Größe in Abhängigkeit des Abstands der Kugelmittelpunkte $r$ zu messen. Dazu verbinden wir den Messschlitten mit Hilfe eines Fadens mit dem Rollwagen. Starten wir nun die Messung, zieht der Messschlitten den Rollwagen entlang der Messschiene. Läuft der Faden entlang/parallel der Messschiene, so bewirkt eine Bewegung des Messschlittens um 1 cm auch eine Vergrößerung von $r$ um 1 cm. Da wir den initialen Abstand $r_{0}$ kennen, können wir nun zu jedem Messpunkt den Abstand der Kugelmittelpunkte $r$ an der x-Achse des aufgetragenen Graphen ablesen.

Bei dem Aufbau ist darauf zu achten, dass der Faden gespannt ist, jedoch den Rollwagen nicht vom Klemmreiter/Stopper entfernt, sonst ändert sich $r_{0}$, der initiale Abstand der Kugelmittelpunkte. Da beide Kugeln positiv geladen sind, stoßen sie sich ab. Um einerseits den Faden zu spannen und andererseits der Abstoßung entgegenzuwirken wird an einem zweiten Faden auf der anderen Seite des Rollwagens ein kleines Massestück befestigt. Der Faden wird über eine am Tisch befestigte Rolle gelegt, das Massestück hängt so an der Seite des Tisches (siehe Detailaufnahme in Abb. 1).

Die Aufzeichnung der Messkurve wurde in dem Aufbau in Abb. 1 zusätzlich mit einer Dokumentenkamera gefilmt und an die Wand projeziert. Wie bereits im didaktischen Teil erwähnt, ist auch eine Aufnahme und Auswertung der Messung mit Cassy möglich. Für weitere Informationen zu dem Aufbau mit Cassy sei auf Leybold (siehe [6], Leybold, Versuch P3.1.2.3) verwiesen. Auch kann dieser Aufbau für die weitere Erarbeitung des Coulombschen Gesetzes genutzt werden. So kann man die Proportionalität der Kraft zur jeweiligen Ladung nachweisen und bei Kombination mit einer Ladungsmessung die elektrische Feldkonstante abschätzen.

Durchführung

Da die zu messenden Kräfte sehr klein sind und der Kraftsensor dementsprechend empfindlich ist, sind störende Einflüsse, wie z.B. Luftzug oder Erschütterungen zu vermeiden. Laut Hersteller (Leybold) muss zudem das hier verwendete Newtonmeter mit angeschlossenem Kraftsensor 30 Minuten warmlaufen (vgl. [7], Handblatt Leybold, Versuch P3.1.2.2).

Zunächst müssen die beiden Kugeln geladen werden. Dafür fahren wir den Rollwagen mit der Kugel zunächst möglichst weit weg. Das Hochspannungsnetzteil wird eingeschaltet. Beide Kugeln werden nacheinander mit 25 kV geladen, indem diese mit der Spitze des Hochspannungskabels berührt werden. Auch hier muss darauf geachtet werden, dass das Kabel den Tisch nicht berührt oder zu nah an leitende Gegenstände kommt. Dies führt zu Überschlägen (beachte dazu auch die Tipps in den Sicherheitshinweisen). Anschließend sollte das Kabel zurück in die Halterung gesteckt werden. Unbedingt ist die Spannung wieder auf Null zu drehen (störende Influenzeffekte, Sicherheit).

Bei dem maximalen Kugelabstand muss das Newtonmeter nun genullt werden. Danach wird der Rollwagen auf den Abstand $r_{0}$ zurückgeschoben. Im Zusammenspiel mit dem x-y-Schreiber hat sich der mittlere Messbereich bis 200 mN angeboten. Die gemessenen Werte bei minimalem Abstand lagen bei ca. 7 mN. Auch ist es sinnvoll das Newtonmeter auf der Einstellung Slow zu betreiben. Dadurch wird ein übermäßig schnelles Zittern des Stifts des x-y-Schreibers vermieden.

Nun muss noch die Einstellung des x-y-Schreibers angepasst werden. Als erstes wählen wir die Geschwindigkeit für den Vorlauf des Messschlittens, für eine schöne Kurve haben sich $0,5\ {\frac {s}{cm}}$ bewährt. Als Richtwert für den y-Messbereich dient $10\ {\frac {mV}{cm}}$ und zwar auf der Stelltung "cal" (kalibrierter Messbereich). Als erstes muss bei genulltem Newtonmeter nun die Nullpunktstellung mit Hilfe des Drehreglers am x-y-Schreiber eingestellt werden. Steht der Stift bei 0 Newton auf dem Nullpunkt des Millimeterpapiers, werden die geladenen Kugeln zusammengeschoben. Bleibt der Stift bei maximaler Kraft innerhalb des Messbereichs, wird nun auf die Schalterstellung "var" (variabler Messbereich) umgestellt. Nun kann mit Hilfe des zweiten Drehreglers langsam ein Vergrößerungsfaktor so eingestellt werden, dass der gesamte zur Verfügung stehenden Messbereich des Schreibers ausgenutzt wird. Die Skala entspricht nun natürlich nicht mehr den eingestellten 10 mV/cm, sondern bspw. 12 mV/cm bei einem Vergrößerungsfaktor von 1,2. Der Vergrößerungsfaktor kann schnell errechnet werden, wird aber in der Auswertung nur zur Fehlerrechnung benötigt. Soll der Versuch mit einer Fehlerrechnung ausgewertet werden, muss an dieser Stelle zu jeder Messreihe der erste Messwert bei $r_{0}$ notiert werden. Die Nullpunktstellung und die Passung des Messbereichs sollte vor jeder Messung geprüft und ggf. angepasst werden. Auch muss das Newtonmeter vor jeder Messung genullt werden. In der Regel ist nur das Finden der besten Einstellung bei der ersten Durchführung etwas aufwändiger, wenn nichts verstellt wird, geht es anschließend schnell.

Bei eingelegtem Millimeterpapier wird die Messung nun gestartet.

Obige Werte zur Einstellung z.B. des x-y-Schreibers sind nur Richtwerte, die sich bei der Durchführung bewährt haben. Insbesondere bei der Verwendung anderer Geräte können diese auch nur als solche dienen.

Ergebnisse

Abb. 2: Beispiel einer Messung

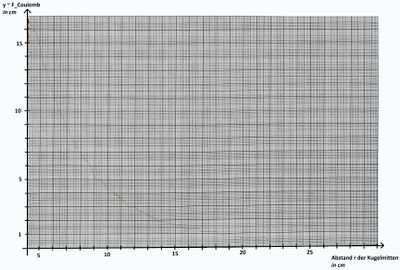
Abb. 2 zeigt ein Beispiel einer Messkurve auf Millimeterpapier. Beim ersten Betrachten wird klar, dass es zumindest möglich ist, dass es sich um die erwartete ${\frac {1}{r^{2}}}$-Abhängigkeit handeln könnte.

Folgende Messwerte wurden aus einer weiteren Messkurve alle 0,5 cm abgelesen und für die Auswertung im folgenden Kapitel verwendet. Dabei wird der Wert der Coulombkraft nicht in Newton angegeben, da dieser mit Hilfe des beim x-y-Schreiber eingestellten Vergrößerungsfakors erst berechnet werden müsste. Da wir aber nur deduktiv nachweisen wollen, dass es sich um eine ${\frac {1}{r^{2}}}$-Abhängigkeit handelt, ist diese Umrechnung überflüssig. Daher werden die Werte der Coulombkraft wie folgt angegeben: $y\sim F_{Coulomb}$ mit $[cm]\sim [N]$.

${\text{Abstand}}\ \ r$ [cm] $y\sim F_{Coulomb}$ [cm] ~ [N] 4,0 16,20 4,5 16,00 5,0 14,40 5,5 12,70 6,0 11,10 6,5 9,80 7,0 8,70 7,5 7,70 8,0 6,80 8,5 6,20 9,0 5,30 9,5 4,90 10,0 4,30 10,5 4,00 11,0 3,60 11,5 3,00 12,0 2,90 12,5 2,60 13,0 2,40 13,5 2,10 14,0 1,90 14,5 1,80 15,0 1,65 15,5 1,50

${\text{Abstand}}\ \ r$ [cm] $y\sim F_{Coulomb}$ [cm] ~ [N] 16,0 1,30 16,5 1,40 17,0 1,10 17,5 1,10 18,0 1,10 18,5 0,85 19,0 1,00 19,5 0,80 20,0 0,65 20,5 0,65 21,0 0,60 21,5 0,70 22,0 0,55 22,5 0,55 23,0 0,55 23,5 0,50 24,0 0,60 24,5 0,40 25,0 0,50 25,5 0,45 26,0 0,40 26,5 0,35 27,0 0,40 28,0 0,20

Auswertung

Qualitative Auswertung

Für eine (erste) eher qualitative Auswertung betrachten wir die Messwerte in den Abständen $r_{1}=5\ cm$, $r_{2}=2\cdot r_{1}=10\ cm$ und $r_{3}=3\cdot r_{1}=15\ cm$. Zur Bestätigung der Proportionalität zu ${\frac {1}{r^{2}}}$ erwarten wir folgendes Ergebnis:

$F_{r_{2}}={\frac {1}{4}}\cdot F_{r_{1}}$ und $F_{r_{3}}={\frac {1}{9}}\cdot F_{r_{1}}$.

Dies kann über mehrere Messreihen schnell mit Hilfe einer Exceltabelle geprüft werden. Wir erhalten folgendes Ergebnis (die Werte der Coulombkraft sind wie oben beschrieben "in cm" angegeben):

Messreihe	$F_{r_{1}}$	$F_{2r_{1}}$	$F_{3r_{1}}$	${\frac {F_{2r_{1}}}{F_{r_{1}}}}$	${\frac {F_{3r_{1}}}{F_{r_{1}}}}$
1	14,4	4,3	1,7	0,30	0,12
2	14,8	4,3	1,5	0,29	0,10
3	15,4	4,5	1,4	0,29	0,09
4	15,2	4,6	1,7	0,30	0,11
5	14,6	4,4	1,6	0,30	0,11
6	16,2	4,6	1,8	0,28	0,11
7	14,3	4,3	1,6	0,30	0,11
			Mittelwert	0,30	0,11
			Zielwert	0,25	0,11
			Abweichung	18,29%	-2,96%

Abb. 3: Veränderte Ladungsverteilung durch Influenzwirkung bei kleinen Abständen $r$

Obige Werte sprechen durchaus für eine Bestätigung des Coulombschen Gesetzes. Es fällt jedoch auf, dass der Mittelwert der Messwerte der Coulombkraft beim doppelten Abstand $r_{1}$ um fast 20 % von dem Zielwert abweicht, der Mittelwert bei dreifachem Abstand nur sehr geringe Abweichungen hat. Gleichzeitig streuen die Messwerte selbst bzw. die Verhältnisse der Coulombkräfte in verschiedenen Abständen (Spalte 4 und 5 obiger Tabelle) kaum. Bei doppeltem Abstand liegt das Verhältnis ${\frac {F_{2r_{1}}}{F_{r_{1}}}}$ immer deutlich über dem Zielwert von 0,25, nie darunter. Auch stellen wir bei Analyse der Unsicherheiten (siehe Kapitel Quantitative Auswertung) fest, dass die Abweichungen bei doppeltem Abstand nicht mit Hilfe dieser zu erklären sind, da die Werte deutlich außerhalb der Fehlerintervalle liegen. Dies legt die Vermutung nahe, dass bei der Messung zusätzlich ein systematischer Fehler existiert, der aber nur bei geringen Abständen der Kugelmittelpunkte zum Tragen kommt.

Eine mögliche Erklärung dieser Systematik ergibt sich bei einem erneuten Blick auf den Versuchsaufbau und das Coulombgesetz. Dieses gilt nur für Punktladungen bzw. kugelsymmetrische Ladungsverteilungen. Von Punktladungen kann aber nur dann näherungsweise ausgegangen werden, wenn der Abstand der Kugelmitten groß im Vergleich zum Kugelradius ist. Dies ist bei kleinen Abständen nicht der Fall. Insbesondere bei kleinen Abständen weicht die Ladungsverteilung auf den Kugeln stark von einer kugelsymmetrischen Verteilung ab, da im Nahfeld eine starke Influenzwirkung auftritt (siehe Abb. 3). Diese verringert sich auch quadratisch mit ${\frac {1}{r^{2}}}$, daher reduziert sich die Influenzwirkung schnell mit größeren Abständen. Es kann dann näherungsweise von einer kugelsymmetrischen Verteilung bzw. von einer Punktladung ausgegangen werden.

Abb. 4: Beispielhafte Auswertung einer Messung

Quantitative Auswertung

Um diese Theorie zu verifizieren, wird die unter Ergebnisse angegebene Messreihe genauer untersucht. Betrachten wir zunächst die Messunsicherheiten. Bei der Messung der Coulombkraft ~ y-Wert in cm treten folgende Unsicherheiten auf:

• ein Ablesefehler von 0,05 cm (Millimeterpapier)
• Unsicherheit des x-y-Schreibers, dieser hat bei der Messung stark "gezittert", nach Beobachtung der Amplitude gehen wir hier von einer Unsicherheit von 0,2 cm aus.
• Unsicherheit des Newtonmeters: Das Newtonmeter hat um bis zu 2 Digits geschwankt, was 0,2 mN entspricht. Umgerechnet in cm (mit Hilfe des Vergrößerungsfaktors bzw. der Skalierung der y-Achse) entspricht dies für obige Messreihe ca. 0,47 cm. Den Vergrößerungsfaktor jeder Messreihe erhalten wir aus dem mitgeschriebenen maximalen Messwert in mN bei $r_{0}$ über den Quotienten des y-Werts in cm dividiert durch den Messwert in mN (hier ${\frac {16,2\ cm}{6,8\ mN}}$).

Mit pythagoräischer Addition ergibt sich eine Gesamtunsicherheit für den y-Wert von rund 0,52 cm. Die Unsicherheit des x-Wertes wird mit 0,2 cm abgeschätzt (Zittern des x-y-Schreibers und Ablesefehler).

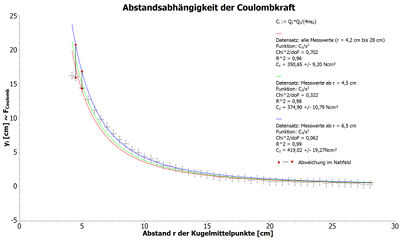
Nun tragen wir die Messwerte mit Unsicherheiten auf und fitten diese mit einer ${\frac {1}{r^{2}}}$-Funktion (siehe Abb. 4). Beziehen wir alle Messwerte in den Fit mit ein, so erhalten wir die rote Kurve (Abb. 4). Es ist zu erkennen, dass der Graph erst für Werte r > 11 cm innerhalb der Fehlerbalken liegt. Dies ist unbefriedigend, da bei diesen Werten die Gesamtunsicherheit bereits in beide Richtungen mindestens 20 % beträgt. Diese Kurve wäre also zur Bestätigung des Coulombzusammenhangs nicht sehr aussagekräftig.

Beziehen wir nun aber unsere Vermutung über den systematischen Fehler mit ein, indem wir die ersten Messwerte (r < 4,5 cm bei der grünen Kurve, r < 6,5 cm bei der blauen Kurve, Abb. 4) nicht in den Fit mit einbeziehen, so erhalten wir ein sehr gutes Ergebnis (Fit-Parameter sind in Abb. 4 zu entnehmen). Die Werte für r < 6,5 cm liegen systematisch unterhalb der blauen Kurve, die Coulombkraft wird also durch die entgegenwirkende Influenz in den Kugeln reduziert. Auch ist der Grafik deutlich zu entnehmen, dass der Effekt stärker wird, je kleiner der Abstand ist. Die Abweichung im Nahfeld ist beispielhaft für zwei Messwerte in Abb. 4 veranschaulicht (vertikale Linien mit roten Dreiecken).

Die genauere Auswertung untermauert also einerseits die Vermutung über den systematischen Fehler durch die Reduzierung der Ladung auf die Kugelmittelpunkte, der im Nahfeld zum tragen kommt. Andererseits zeigt die Auswertung, dass das Experiment zur Bestätigung des Coulombschen Gesetzes für hinreichend große Abstände sehr gut geeignet ist und damit, wie im didaktischen Teil behauptet, die Messgenauigkeit des x-y-Schreibers ausreichend ist. Es bestätigt sich auch, dass sich ein Fokus auf die Datenauswertung aufgrund vielfältiger Unsicherheiten nicht nur anbietet, sondern für einen quantitativen Nachweis des Coulombgesetzes nötig ist.

Sicherheitshinweise

Bei dem Versuch wird mit Hochspannung gearbeitet (25 kV)! Das Kabel zum Laden der Kugeln (in diesem Aufbau) ist zwar bereits ein Hochspannungskabel, jedoch auch nur bis 1kV geeignet. Die Folge sind Überschläge zum Tisch, zur Hochspannungsquelle und natürlich auch zum Experimentator. Das kann auch schon mal etwas unangenehm sein. Nach meiner Erfahrung lassen sich die (unangenehmen) Stromschläge vermeiden, wenn man Schuhe mit dicken Sohlen (z.B. Winterboots) trägt. Die geladenen Kugeln sollten nach dem Experimentieren immer mit einer Erdung entladen werden. Auch hier kann es sonst bei Berührung zu Stromschlägen kommen.

Daher ist dieses Experiment nicht als Schülerexperiment geeignet.

Siehe auch

• Leybold, Versuch P3.1.7.3: https://www.ld-didactic.de/documents/de-DE/EXP/P/P3/P3173_e.pdf [02.04.2017]
• Leybold, Versuch P3.1.2.2: http://www.ld-didactic.de/phk/gruppen.asp?PT=VP3.1.2.2_a&L=1 [07.03.2014]
• Leybold, Versuch P3.1.2.2, Handblatt: http://www.ld-didactic.de/documents/de-DE/EXP/P/P3/P3122_d.pdf [07.03.2014]
• Leybold, Versuch P3.1.2.3: http://www.ld-didactic.de/phk/gruppen.asp?PT=VP3.1.2.3&L=1 [07.03.2014]