Innenwiderstand einer Batterie

Innenwiderstand einer Batterie
Abb.1: AA Batterie Auch eine handelsübliche Batterie hat einen Innenwiderstand
Kurzbeschreibung
Mit diesem einfachen Experiment soll den Schüler gezeigt werden, dass jede Spannungsquelle auch den das System durch ihren Innenwiderstand beeinflusst. Dadurch soll den Schülern auch die Augen geöffnet werden Systeme immer genau zu hinterfragen.
Kategorien
Elektrizitätslehre Spannung, Stromstärke und Widerstand (URI)
Einordnung in den Lehrplan
Geeignet für:	möglich bereits in Klasse 10 als Vertiefung des Themas Stromkreise
Basiskonzept:	System
Sonstiges
Durchführungsform	primär Demoexperiment, auch als Schüler- bzw. Gruppenexperiment durchführbar
Anzahl Experimente in dieser Unterkategorie	2
Anspruch des Aufbaus	leicht
Informationen
Name:	Heiner Krüger
Kontakt:	Heiner_Krueger@gmx.de
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Johannes Schulz

Die meisten der Schüler haben kein Bewusstsein dafür, dass Messgeräte sowie Spannungsquellen einen Innenwiderstand haben. Dies liegt daran, dass dies selten ausführlich erwähnt wird, da es kaum Auswirkungen auf die Messungen im Unterricht hat. Dieser Versuch soll am Beispiel der Batterie dem Schüler deutlich zeigen, dass jede Spannungsquelle von sich aus einen gewissen Innenwiderstand hat. Wie wichtig es sein kann den Innenwiderstand der Spannungsquelle zu bestimmen zeigt zum Beispiel die Entscheidung der Drahtwahl bei einer Styroporsäge (siehe didaktischer Teil).

Didaktischer Teil

Wie bereits im Vortext erwähnt, haben die Schüler kein Bewusstsein dafür, dass Spannungsquellen sowie auch Messgeräte einen Innenwiderstand haben. Dies ist jedoch ein verbreitetes Problem im Physikunterricht, denn Schüler vergessen häufig, dass wir in der Physik zumeist mit vereinfachten Modellen arbeiten müssen, um uns Sachverhalte erklären zu können und bestimmte Formeln herzuleiten. Also dürfen die Schüler nie vergessen, dass unser Wissen über die Realität zumeist hypothetisch ist (vgl. Girwidz (2010), S. 736). An dieser Stelle soll ein kurzes Experiment vorgestellt werden, welches zu der Erkenntnisgewinnung führt, dass es scheinbar einen weiteren Widerstand in unserem Stromkreis gibt als die uns bisher bekannten. Dabei handelt es sich um das Experiment der Styroporsäge, welches den Schülern die Augen öffnen soll.

Eine Styroporsäge ist eine Säge, welches mit Hilfe von Wärme funktioniert. Dafür wird ein Draht an eine Spannungsquelle (z.B. Batterie) angeschlossen, wodurch ein Strom durch den Draht fließt und der Draht heiß läuft. Die Leistung im Draht lässt sich berechnen durch $P=U\cdot I$, somit ist die Vermutung, dass der Draht am besten schneidet wenn dieser Wert am höchsten ist.

Nun lassen wir die Schüler unterschiedliche Drähte in eine Styroporsäge einspannen um dann mit dieser ein Stück Styropor zu schneiden. Was schnell klar wird ist, dass die Schneidefähigkeit variiert je nach Dicke und Material des Drahtes, was darauf schließen lässt, dass es vom Widerstand des Drahtes abhängt. Nach den Messungen wird jedoch auch klar, dass weder ein sehr niedriger, noch ein sehr hoher Widerstand das beste Ergebnis bringt. Dabei hätte man in der Vorüberlegung denken können, dass ein hoher Widerstand dafür sorgt, dass kaum Stromfluss herrscht und dadurch die Leistung gering bleibt. Somit müsste der Widerstand möglichst gering gewählt werden, damit die Stromstärke möglichst groß wird und somit die Leistung möglichst groß wird, jedoch zeigt das Experiment dass die Schneidefähigkeit des Drahtes nachlässt wenn der Widerstand zu gering wird.

Somit scheint es einen weiteren Aspekt in unserem Stromkreis zu geben welchen wir bisher außer Acht gelassen haben. Somit bleibt die Untersuchung der Batterie aus. Es stellt sich also die Frage: was könnte der Grund dafür sein, dass die Leistung scheinbar auch im niedrigen Widerstandsbereich zusammenbricht? Hierfür messen wir die Klemmenspannung und die Stromstärke in den Drähten und stellen fest, dass die Klemmenspannung zusammenbricht. Dies kann nur der Fall sein wenn die Spannung an einem anderen Ort abfällt. Wir kommen also zu der Erkenntnis, dass die Spannungsquelle scheinbar einen Widerstand hat, an welchem die Spannung dann abfällt. Somit haben wir einen Grund gefunden, weshalb es wichtig ist den sogenannten Innenwiderstand dieser Spannungsquelle zu bestimmen. Denn die Leistung wird am größten wenn das Verhältnis ${\frac {R_{\text{i}}}{R_{\text{a}}}}=1$ ist, also $R_{\text{i}}=R_{\text{a}}$ ist. Man muss also den Innenwiderstand bestimmen um den „perfekten“ Draht auszusuchen um mit der Styroporsäge zu schneiden.

Die abschließende Erkenntnis ist also:

Jede Spannungsquelle hat einen Innenwiderstand und es ist wichtig für uns zu wissen wie wir diesen bestimmen.

Versuchsanleitung

Aufbau

benötigte Geräte

Zumeist wurden Geräte von PHYWE verwendet

• 1 Steckbrett
• 1 Batteriehalterung für 4 AA Batterien
• 4 Batterien (AA)
• 1 Satz Steckbrücken
• 1 Voltmeter
• 1 Amperemeter
• 1 stufenlos regelbaren 500 Ω Widerstand
• 1 Schalter
• 4 Steckkabel zur Verbindung der Messgeräte

Aufbau

Abb.2: Schaltskizze

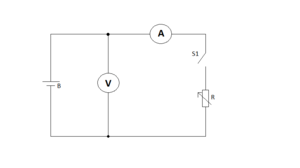
Der Aufbau der Versuchsanordnung entspricht der Schaltung nach Abb.1. Hierbei ist zu sehen, dass die Batterien (AA Batterien) als Spannungsquelle fungieren und zu ihnen parallel ein Voltmeter geschaltet wird. Weiterhin werden in Reihe ein Amperemeter und ein regelbarer ohmscher Widerstand (500 $\Omega$) geschaltet. In den Teil des Stromkreises mit dem Widerstand wird ein Schalter eingebaut, sodass die Batterie nur belastet wird wenn der Schalter geschlossen ist. Dieser Schalter ist da um zu sichern, dass die Spannung immer nur für kurze Zeit eingeschaltet ist, denn besonders bei geringen Widerständen wird viel Energie der Batterie verbraucht, was dafür sorgen würde, dass die Leerlaufspannung der Batterie zurückgeht. Dies soll durch kurze Messzeiten verhindert werden.

Durchführung

Standarddurchführung des Experiments

Zu Beginn des Experiments sollte der Schalter geöffnet sein und die Batterie noch nicht in den Batteriehalter eingelegt sein. Bevor die Batterie eingelegt wird müssen die Messgeräte auf einen geeigneten Bereich eingestellt werden. Die Spannung wird hierbei kleiner als 2 V bleiben und die Stromstärke sollte 300 mA nicht übersteigen.

Nun kann die Batterie in die Halterung eingesetzt werden, wobei der Schalter zunächst geöffnet bleibt. In diesem Zustand wird zuerst die Leerlaufspannung der Batterie gemessen und notiert. Nun wird der regelbare Widerstand in regelmäßigen Abständen (z.B. 50 $\Omega$ Schritte) gesteigert. Auf jeder Stufe wird der Schalter einmal kurz umgelegt und es werden schnellstmöglich Spannung und Stromstärke notiert. Dieser Vorgang wird wiederholt bis das Maximum des Widerstandes erreicht ist.

Alternative

Abb.3: Schaltskizze der alternativen Messmethode

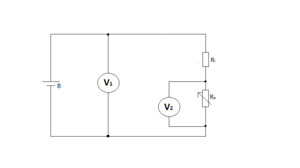
Für die Alternative Messvariante wurde ein weiteres Schaltbild erstellt (siehe Abb.3). Der einzig erkennbare Unterschied ist, dass nun kein Schalter mehr eingebaut ist und dass der Innenwiderstand der Batterie durch Ri dargestellt ist, dies dient zum besseren Verständnis dieser Methode. Bei dieser Methode nutzen wir den Fakt aus, dass die beiden Widerstände nun einen Spannungsteiler bilden. Die Batterie wird wie schon zuvor wieder in die Halterung eingesetzt, sobald die Messgeräte in die richtigen Bereiche eingestellt wurden (siehe Durchführung). Erneut wird vor erhöhen des Widerstandes die Leerlaufspannung der Batterie gemessen und notiert. Nun wird der regelbare Widerstand solange erhöht bis an ihm genau die Hälfte der Leerlaufspannung abfällt. Wenn dies eingestellt wurde wird der eingestellte Widerstand notiert (für das weitere Vorgehen siehe Auswertung Alternative).

Durchführung als Schülerexperiment

Als Schülerexperiment ändert sich am generellen Ablauf nicht viel. Es sollten viel eher beide Möglichkeiten kombiniert werden. Dafür sollten zuvor beide Methoden mit den Schülern diskutiert werden und die Vor- sowie Nachteile erläutert werden. Dann werden die Schüler in zwei Gruppen aufgeteilt, wobei die Gruppen je eine Methode nutzen um den Innenwiderstand zu bestimmen. Innerhalb der Gruppen wäre es am besten wenn die Schüler in 2er Gruppen arbeiten, sofern genug Geräte vorhanden sind. Nach der Auswertung ihrer Ergebnisse sollten sich die Schüler über diese austauschen.

Ergebnisse

U in V	u(U) in V	I in mA	u(I) in mA
1,09	0,01	0	0
1,089	0,005	1,13	0.05
1,085	0,005	3,94	0,05
1,077	0,005	7,70	0,05
1,065	0,005	12,50	0,05
0,988	0,005	38,30	0,05
0,663	0,005	182,00	0,05
0,510	0,005	248,42	0,05

Auswertung

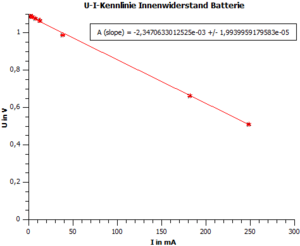
Für die Auswertung verwenden wir unsere gemessenen Werte für die Spannung und die Stromstärke. Mit Hilfe dieser Werte erstellen wir die U-I-Kennlinie. Dies bedeutet wir tragen U in Abhängigkeit von I ab (U auf die y-Achse, I auf die x-Achse). Dies wurde beispielhaft für die Messwerte aus Tabelle1 in dem Diagramm aus Abbildung4 dargestellt (Messwerte für die 4 handelsüblichen AA Batterien). Nun gibt es zwei Möglichkeiten aus diesem Graphen den Innenwiderstand der Batterie zu bestimmen. Doch bevor wir zu diesen kommen, ein kurzer Exkurs zur allgemeinen Berechnung des Innenwiderstandes: Wir können uns den Innenwiderstand der Batterie und unseren regelbaren Widerstand als zwei in Reihe geschaltete Widerstände vorstellen wodurch sich folgende Formel für den Gesamtwiderstand ergibt:

$R_{\text{i}}=R_{\text{ges}}-R_{\text{a}}$

Diagramm 1: linearer Fit zu der Tabelle aus Ergebnisse

Wenn wir diese umstellen ergibt sich:

$R_{\text{i}}={\frac {U_{\text{0}}}{I_{\text{l}}}}-{\frac {U_{\text{l}}}{I_{\text{l}}}}={\frac {U_{\text{0}}-U_{\text{l}}}{I_{\text{l}}}}$

Und wenn wir diese ein wenig weiter umstellen ergibt sich zum Schluss:

$R_{\text{i}}={\frac {(U_{\text{0}}-U_{\text{l}})*R_{\text{l}}}{U_{\text{l}}}}={\frac {U_{\text{0}}}{I_{\text{K}}}}$

Wobei U₀ und I_K die Leeerlaufspannung und der Kurzschlusstrom sind. Diese beiden Größen lassen sich mit Hilfe der Funktion des Graphen ablesen. Denn sie entsprechen den beiden Achsenschnittpunkten. Der Schnittpunkt mit der x-Achse ist die Leerlaufspannung, da die Stromstärke und somit die Belastung 0 sind. Der Schnittpunkt mit der y-Achse ist der Kurzschlussstrom. Somit kann man mit Hilfe des geplotten Graphen beide Schnittpunkte bestimmen und den Quotienten bilden um den Innenwiderstand der Batterie zu bestimmen. Der sinnvollere Weg ist den Innenwiderstand direkt abzulesen. Denn der Quotient aus Kurzschlusstrom und Leerlaufspannung ist der Quotient aus Nullstelle und Schnittpunkt mit der y-Achse also handelt es sich um den Anstieg der Gerade welcher direkt abzulesen ist. In unserem Beispiel handelt es sich also um

$R_{\text{i}}=(2,35\pm 0,02)\Omega$

Der Fehler der Messwerte ergab sich hierbei aus einer Abschätzung von einem halben Skalenteil des letzten Digits des Anzeigegerätes. Dieser Fehler ist möglicherweise ein wenig zu klein abgeschätzt, da sicherlich ein gewisser Prozentsatz des Messbereichs noch aufgerechnet werden müsste, doch steht der genaue Wert dieses Prozentsatzes nicht zur Verfügung. Für diese Experimentierreihe wurde eine Batteriehalterung mit 4 Batterien (AA) verwendet. Da nicht bekannt ist wie erschöpft die Batterien waren und es auch keinen Referenzwert gibt wie hoch der Innenwiderstand einer solchen Vorrichtung ist, ist es schwer zu sagen ob das Ergebnis unseren Erwartungen entspricht. Jedoch kann man auf jedenfall sagen, dass wir nachgewiesen haben, dass es einen gewissen Innenwiderstand gibt, welchen man bei Messungen innerhalb eines Stromkreises nie ganz vernachlässigen bzw. vergessen sollte.

Alternative

Diese Methode ist in der Auswertung um einiges kürzer als die vorangegangene. Dadurch, dass wir den Widerstand so eingestellt haben, dass an ihm die Hälfte der Leerlaufspannung abfällt und wir nur zwei Widerstände haben muss an dem anderen Widerstand die gleiche Spannung abfallen. Da die Stromstärke in einer Reihenschaltung immer konstant ist gilt: U_a = U_i und I_i = I_a, da diese beiden Größen gleich groß sind und die Formel für den Widerstand :$R={\frac {U}{I}}$ ist sind auch beide Widerstände jetzt gleich groß: R_a = R_i. Den Außenwiderstand haben wir selbst eingestellt und können ihn somit ablesen, dadurch wissen wir auch direkt welchen Innenwiderstand die Batterie hat. Man kann anstatt den Widerstand abzulesen auch wieder U und I messen um ihn zu errechnen. Hierbei kommt der Fehler darauf an wie genau der reguläre Widerstand einzustellen ist. Da diese Alternative nur ein Vorschlag ist und nicht selbst durchgeführt wurde kann an dieser Stelle kein genauer Fehler angegeben werden. Dieser ist dann aus dem Handbuch des Widerstandes zu entnehmen.

Vergleich der beiden Methoden

Wenn man beide Methoden direkt miteinander vergleicht fällt sofort auf, dass die zweite Methode die eindeutig kürzere ist. Jedoch hat man dafür bei der ersten Methode mehr Messwerte was somit zu einem genaueren Ergebnis führen kann, da sich über die lineare Regression einzelne Ausreißer besser kompensieren lassen. Diesem Nachteil kann man aber entgegenwirken indem man bei der zweiten Methode mehrere Messungen hintereinander ausführt und aus den Ergebnissen dann das arithmetische Mittel bestimmt. Weiterhin umgeht man bei der zweiten Methode das Problem, dass die Leerlaufspannung der Batterie geringer wird, da man nur eine kurze Messung macht und nicht mehrere Messungen hintereinander. Somit lässt sich als Fazit sagen, dass die zweite Methode zu bevorzugen ist, da sie nicht so zeitaufwendig ist wie die erste. In der Schule sollte jedoch auch die erste Methode durchgeführt werden, da dies eine sehr gute Übung ist um zu lernen Messwerte aufzunehmen und diese richtig auszuwerten, was ein wichtiger Punkt des Rahmenlehrplans ist (siehe auch:[1]Rahmenlehrplan Berlin SekI).

Sicherheitshinweise

Außer den typischen Risiken beim hantieren mit Spannung und Strom gibt es in diesem Experiment keine weiteren Sicherheitsrisiken. Wenn dieses Experiment als Schülerexperiment durchgeführt wird ist darauf zu achten, dass jede einzelne Schaltung vor Inbetriebnahme durch den Lehrer kontrolliert wird. So werden nicht nur die Schüler sondern auch die Geräte vor möglichen Schäden bewahrt.

Siehe auch

• Rahmenlehrplan Berlin SekI; https://www.berlin.de/imperia/md/content/sen-bildung/schulorganisation/lehrplaene/sek1_physik.pdf?start&ts=1447852932&file=sek1_physik.pdf [30.03.2016]

Mehr Vorschläge zur Bestimmung des Innenwiderstandes:

• [Hobby Bastelecke - Innenwiderstand von Spannungsquellen]