Induktion durch Flussänderung
| Diese Experimentieranleitung befindet sich im Entstehen und wurde noch nicht freigeschaltet..
Solltest du Fragen zu dem Thema haben, nimm am besten Kontakt mit dem Autor oder der Autorin auf. |
| Induktion durch Flussänderung | |
| Abb.1 Versuchsaufbau | |
| Kurzbeschreibung | |
|---|---|
| Durch das Analysieren verschiedener Messreihen wird das Induktionsgesetz vertieft. | |
| Kategorien | |
| Elektrizitätslehre, Induktion | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II usw. |
| Basiskonzept: | System, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Demoexperiment, SchülerInnen-Experiment, Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Marco Thiesen |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Daniel Zechlin |
In diesem Versuch soll das Phänomen der elektromagnetischen Stromerzeugung behandelt werden. Insbesondere wird die Erzeugung einer Gleichspannung durch Änderung der magnetischen Feldstärke näher betrachtet. Dieser Versuchsaufbau eignet sich dazu, durch die quantitative Auswertung verschiedener Versuchsreihen, experimentell das Induktionsgesetz, was 1831 unter anderem von Michael Faraday begründet wurde, zu untermauern (vgl./siehe Kuhn, W.[1] 1998, Seite 137).
Inhaltsverzeichnis
Didaktischer Teil
In der Schule wird das Induktionsgesetz in der Regel eingeführt, nachdem magnetische- und elektrische Felder behandelt wurden. Das hier beschriebene Experiment bedarf einiger Vorkenntnisse, die da wären:
- Die physikalischen Phänomene des Magnetismus – Kräftewirkung und Bewegung elektrischer Ladung.
- Elektrisches Feld und deren Eigenschaften.
- Elektromagnetische Induktion – Aufbau eines elektrischen Feldes, bei Veränderung der magnetischen Flussdichte. (s.Elektromagnetische Induktion)
Der Grundriss der elektromagnetischen Induktion kann durch geeignete qualitative Experimente geliefert werden.
Das Experiment bietet sich als Lehrerdemonstrationsexperiment oder auch als SchülerInnenexperiment in Gruppenarbeit an, um mehrere Lernziele zu fördern. Ein großer Teil der geforderten Kompetenzen zählt zu der Erkenntnisgewinnung. Der didaktische Schwerpunkt in diesem Experiment liegt unter anderem darin Zusammenhänge der Induktion zu verinnerlichen und anzuwenden. Jedoch liegt hier der Schwerpunkt im Erlangen von Kompetenzen im Bereich der Datenauswertung sowie der grafischen Darstellung von Daten. Hat man diesen Versuch erst einmal aufgebaut und die nötigen Messungen durchgeführt, was die Fähigkeiten der SchülerInnen im Planen und Durchführen von Experimenten bestärkt, steht man vor einer große Menge von Daten, die analysiert werden müssen. Darin besteht die eigentlich Arbeit des Experiments. Da in diesem Experiment das Cassy2 verwendet wird, was ein computergestütztes Messwerterfassungssystem ist, lassen sich schnell viele Messungen durchführen. Diese Messungen sind zudem frei von Ableseungenauigkeiten. Die Datenaufnahme mit dem Cassy2 und dem Laptop erfordert außerdem zusätzliche Fähigkeiten im Bereich der Informationstechnik. Des Weiteren werden durch die Bearbeitung der Ergebnisse physikalische Zusammenhänge gestärkt und gefestigt. Die Auswertung des Experiments eignet sich auch als Gruppenprojekt, wobei man zusätzlich im Rahmen einer Projektvorstellung die Präsentationsfähigkeit der SchülerInnen fördert.
Versuchsanleitung
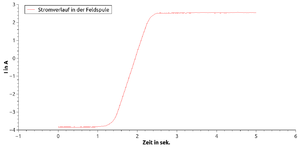
Der hier dargestellte Versuch zeigt den Zusammenhang zwischen der induzierten Spannung bei Flussänderung und der Windungszahl bzw. Querschnittfläche der Induktionsspule. Um die Flussänderung, in der Feldspule, zu realisieren, wird diese an einem Funktionsgenerator angeschlossen, bei dem es möglich ist, eine Dreiecksfunktion zu erzeugen. Die Dreiecksfunktion versorgt die Feldspule mit einem Strom, der linear ansteigt und wieder abfällt, was mit dem Cassy2 gemessen werden kann. Der Stromverlauf ist in der Abb. 2 zu sehen.
Durch die lineare Flussänderung wird in der Spule ein konstanter Strom induziert, der ebenfalls von dem Cassy2 gemessen wird.
In diesem Versuch werden verschiedene Messungen vorgenommen, in dem die Differenz vom minimalen bis zum maximalen Strom immer 6 A beträgt. Jedoch wird durch Änderung der Frequenz am Funktionsgenerator die Zeit, in der der Strom ansteigt bzw. abfällt kürzer oder länger. Je nachdem wie schnell der Strom, in der Feldspule, ansteigt oder abfällt, wird sich eine andere konstante Spannung in der Induktionsspule einstellen. Die verschiedenen Zeiten und Spannungen werden notiert und in der Auswertung analysiert. In der Abb. 3 kann man sehen, wie der Stromverlauf, in der Feldspule und die zugehörige Spannung, aussehen könnte. Dort werden Spannung und Strom auf die y-Achse gelegt, was nicht ganz sauber ist und unbedingt auseinander gehalten werden muss. Jedoch ist es auch ganz anschaulich beides in einer Grafik zu betrachten, da so das Phänomen der Induktion durch Flussänderung deutlicher wird. In der Auswertung können die Ergebnisse verschiedener Messreihen mit unterschiedlichen Spulen genauer analysiert werden und so auf das Induktionsgesetz erfassen.
Aufbau
Materialien
- Cassy 2
- Funktionsgenerator
- Bananenstecker
- Feldspule
- Induktionsspulen (300Wdg.und 28cm³,300Wdg. und 14cm³, 100Wdg. und 28cm³)
- Laptop mit zugehöriger Cassysoftware
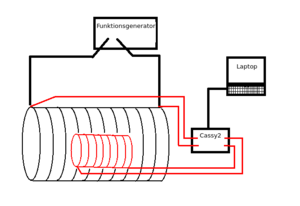
Der Versuch wird wie in dem Schaltbild (Abb.4) bzw. dem Foto (Abb.1) zu sehen ist, aufgebaut. Die Feldspule wird von dem Funktionsgenerator, mithilfe von Bananenstecker, mit Strom versorgt. Der Funktionsgenerator wird für diesen Versuch auf Dreiecksspannung eingestellt. Die Induktionsspule befindet sich in der Feldspule. Das Cassy2 wird an dem einen Eingang an die Feldspule geschlossen, um dort den Stromverlauf zu messen. Und am anderen Eingang an der Induktionsspule, um dort die Induktionsspannung zu messen. Des Weiteren wird das Cassy2 am Laptop angeschlossen, um die Messung mit der zugehörigen Cassysoftware aufzunehmen. Dazu ist es möglich die von Laybold vorgefertigten Einstellungen oder auch seine eigene Einstellungen, die man beliebig vornehmen kann, zu verwenden.
Durchführung
Dazu muss der Funktionsgenerator auf Dreiecksspannung und einer beliebigen Frequenz eingestellt sein. Mit dem in dieser Versuchsanleitung verwendeten Generator wird die Zeit, in der die Feldspule vom minimalen Strom auf einen maximalen Strom gelangt, über die Frequenz gesteuert. An dieser Stelle möchte ich darauf hinweisen, dass es sicherlich bessere Generatoren gibt, bei denen man diese Zeit besser einstellen kann. Wird die Feldspule nun mit Strom versorgt, sieht man dies auch auf dem Bildschirm des Cassy2. Auf diesem Bildschirm sollte nun die Ampereanzeige ständig steigen und wieder abfallen. Jetzt kann man am Laptop die erste Messung, mit den gewünschten Einstellungen, starten und die Daten von dem Programm aufzeichnen lassen. Dies geschieht einmal in grafischer Form und einmal als Tabelle. Beide Datensätze können zur Auswertung verwendet werden. Um diesen Versuch quantitativ auswerten zu können, müssen mehrere Messungen vorgenommen werden. Insgesamt werden 3 verschiedene Spulen gemessen mit je 6 Messungen. Bei jeder dieser 6 Messungen wird die Frequenz am Funktionsgenerator erhöht, damit sich die Zeit, in der der Strom, der Feldspule, vom minimalen Strom auf einen maximalen Strom verringert. Die Spulen unterscheiden sich in der Querschnittfläche und in der Windungszahl.
Ergebnisse
Die Ergebnisse des Versuches kann man in Form einer Tabelle auf dem Laptop anschauen und zur weiteren Bearbeitung beliebig formatieren. In der hier verlinkten PDF-Datei kann ein Beispiel für 6 Messungen, einer Spule mit 300Whd. und einer Querschnittfläche von 28 cm³, mit unterschiedlichen Frequenzen entnommen werden. Hier handelt es sich um einen riesigen Datensatz, der für unterschiedlichste Auswertungen genutzt werden kann. Die Ergebnisse aller Messungen, die für diese Auswertung von Bedeutung sind, wurden für die weitere Auswertung in folgenden Tabellen zusammengefasst:
| Spule mit 300 N=Wdg. und A=28cm³ | ||||||
| Messung | 1 | 2 | 3 | 4 | 5 | 6 |
| Zeit in sek. | 1,4 | 1 | 0,76 | 0,6 | 0,5 | 0,43 |
| Spannung in mV | 840 | 1200 | 1600 | 1980 | 2350 | 2700 |
| Spule mit 300 N=Wdg. und A=14cm³ | ||||||
| Messung | 1 | 2 | 3 | 4 | 5 | 6 |
| Zeit in sek. | 1,7 | 1,2 | 0,88 | 0,7 | 0,6 | 0,5 |
| Spannung in mV | 1900 | 2800 | 3700 | 4550 | 5500 | 6500 |
| Spule mit 100 N=Wdg. und A=28cm³ | ||||||
| Messung | 1 | 2 | 3 | 4 | 5 | 6 |
| Zeit in sek. | 1,31 | 0,9 | 0,7 | 0,52 | 0,45 | 0,39 |
| Spannung in mV | 660 | 990 | 1350 | 1660 | 1900 | 2200 |
Auswertung
Um diesen Versuch auszuwerten und auf das Induktionsgesetz zu schließen werden zu erst die ersten beiden Tabellen aus den Ergebnissen zu den folgenden beiden Tabellen rechnerisch ergänzt zu:
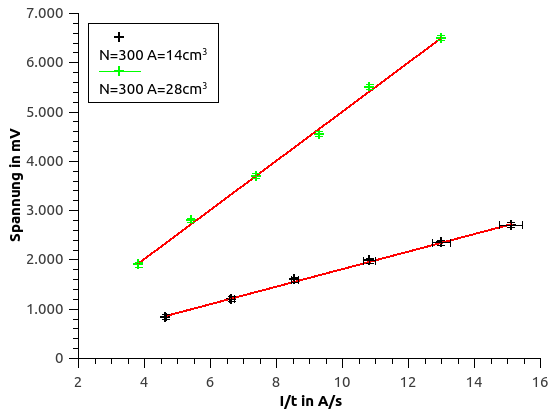
| Spule mit N=300 Wdg. und A=28cm³ | ||||||
| Messung | 1 | 2 | 3 | 4 | 5 | 6 |
| Zeit in sek. | 1,4 | 1 | 0,76 | 0,6 | 0,5 | 0,43 |
| Spannung in mV | 840 | 1200 | 1600 | 1980 | 2350 | 2700 |
| I/t | 4,64 | 6,50 | 8,55 | 10,83 | 13,00 | 15,12 |
| U/(I/t) | 180,92 | 184,62 | 187,08 | 182,77 | 180,77 | 178,62 |
| Spule mit N=300 Wdg. und A=14cm³ | ||||||
| Messung | 1 | 2 | 3 | 4 | 5 | 6 |
| Zeit in sek. | 1,7 | 1,2 | 0,88 | 0,7 | 0,6 | 0,5 |
| Spannung in mV | 1900 | 2800 | 3700 | 4550 | 5500 | 6500 |
| I/t | 3,82 | 5,42 | 7,39 | 9,29 | 10,83 | 13,00 |
| U/(I/t) | 496,92 | 516,92 | 500,92 | 490,00 | 507,69 | 500,00 |
Mit der Tabelle kann nun die Beziehung Uind~ A* (1) nachgewiesen werden. Die wir auch nochmal durch die folgende Grafik verdeutlicht.
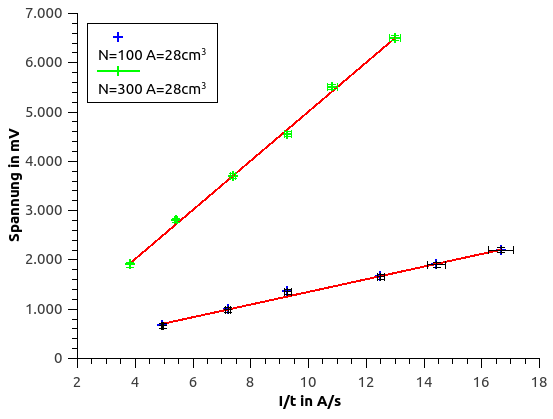
Im zweiten Teil der Auswertung wollen wir die Beziehung Uind ~ N (2) verdeutlichen, wozu wir die dritte Tabelle wieder rechnerisch zu ergänzen. Somit erhalten wir folgende Tabelle:
| Spule mit 100 Whd. und A=28cm³ | ||||||
| Messung | 1 | 2 | 3 | 4 | 5 | 6 |
| Zeit in sek. | 1,31 | 0,9 | 0,7 | 0,52 | 0,45 | 0,39 |
| Spannung in mV | 660 | 990 | 1350 | 1660 | 1900 | 2200 |
| I/t | 4,96 | 7,22 | 9,29 | 12,50 | 14,44 | 16,67 |
| U/(I/t) | 133,02 | 137,08 | 145,38 | 132,80 | 131,54 | 132,00 |
Auch diese Beziehung kann in einer Grafik verdeutlicht werden, dazu werden die Werte aus der zweiten und dritten Tabelle verwendet.
Fast man nun die beiden Erkenntnisse (1) und (2) zusammen erhält man:
Uind ~ N * A *
Was schon fast das Induktionsgesetz ist. Es bleibt nur noch das Minuszeichen zu diskutieren. Dazu eignet sich hervorragend der Versuch zur Selbstinduktion.
Sicherheitshinweise
Wie in alles Experimenten, in denen mit Elektrizität gearbeitet wird ist besondere Vorsicht geboten. Es sollte immer drauf geachtet werden, dass der Funktionsgenerator nur eingeschaltet ist solange er sich in Benutzung befindet.
Literatur
- ↑ Kuhn, W.: Handbuch der experimentellen Physik. Sekundarbereich II, Bd.5/I, Elektrizitätslehre, Aulis, 1998