Induktion (Stabmagnet und Spule)
| Induktion (Stabmagnet und Spule) | |
 Aufbau des Experimentes zur Induktion (Stabmagnet und Spule) | |
| Kurzbeschreibung | |
|---|---|
| Lehrer oder Schüler/innen messen die Spannung an einer Spule, die sich in einem periodisch verändernden Magnetfeld befindet und lassen sich den Graphen der Spannung ausgeben. Dieser wird dann qualitativ mit dem Induktionsgesetz für Spulen fachlich diskutiert und ausgewertet. | |
| Kategorien | |
| Elektrizitätslehre, Induktion | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Demonstrations-Experiment, Schüler*innen-Experiment |
| Anzahl Experimente in dieser Unterkategorie | 3 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Christian Thielecke |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Stephan Pfeiler |
Die elektromagnetische Induktion wurde von Michael Faraday um 1881 entwickelt und steht für die Erzeugung elektrischer Felder aus Magnetfeldern.[1]
Das in diesem Artikel vorgestellte Experiment dient dazu, die schon bekannte allgemeine Induktion durch eine qualitative Auswertung zu vertiefen und darüber hinaus einen Umgang mit anormalen Daten kennen zu lernen. Dies geschieht durch den intuitiv erwarteten sinusförmigen Induktionsspannungsverlauf, denn dieser steht in der Regel nicht im Einklang mit dem tatsächlich gemessenen Verlauf und bedarf daraufhin einer Erklärung. Weiter ist das Experiment durch den einfachen und unkomplizierten Aufbau gut als Demonstrationsexperiment oder als Schüler/innen-Experiment geeignet.
Inhaltsverzeichnis
Didaktischer Teil
Zur Auswertung von Experimenten werden entweder qualitative oder quantitative Methoden verwendet. Dieses Experiment eignet sich mehr für eine qualitative als für eine quantitative Auswertung. Dies liegt mit unter daran, dass der Induktionsspannungsverlauf nur mit einem Polynom höheren Grades beschrieben werden kann und sich somit schwer für eine quantitative Auswertung eignet. Weiter fließt kaum ein messbarer Strom, was im Wesentlichen an der Versuchsanordnung und der daraus resultierenden Induktionsspannung liegt. D.h. auch dieser kann für eine quantitative Auswertung, um z.B. die Induktivität der Spule zu bestimmen, kaum benutz werden.
Weiter sollte das Experiment eher am Ende einer Unterrichtsreihe zur Induktion (Spule) eingesetzt werden. Dies hat den Vorteil der Diskrepanz zwischen der durch den Unterricht aufgebauten Schülervorstellung eines sinusförmigen Induktionsspannungsverlaufes durch ein sich periodisch änderndes Magnetfeld und dem tatsächlich gemessenen Verlauf. Diesen Sachverhalt kann man nutzen um den Umgang mit anormalen Daten zu trainieren. Eine allgemeine Forderung danach erhält man unter anderem aus dem Rahmenlehrplan Physik Bereich Erkenntnisgewinnung:
- Die Schülerinnen und Schüler erfassen natürliche Phänomene oder technische Effekte zielorientiert, indem sie beobachten und messen. Sie werten die Beobachtungs- und Messdaten mithilfe mathematischer oder vergleichender Methoden aus. Sie reflektieren die Ergebnisse und setzen sie in Beziehung zu vorhandenen Erkenntnissen. Sie entwickeln dabei neue Modelle oder modifizieren vorhandene. Mithilfe von Modellen beschreiben, erklären und prognostizieren sie natürliche Phänomene und technische Effekte. (Rahmenlehrplan Berlin 2010, Physik, S.10)
Mit anormalen Daten ist gemeint: Daten die eine Abweichung von der Regel oder von üblichen Theorien darstellen.[2] Es gibt nach C. Chinn und W. Brewer allgemein sieben Möglichkeiten wie Individuen mit anormalen Daten umgehen können:[3]
- a) Ignorieren der Daten
- b) Ablehnen der Daten
- c) Ausschluss der Daten aus der aktuellen Theorie
- d) Hinnehmen der Daten ohne weitere Konsequenzen
- e) Neuinterpretieren der Daten
- f) Peripherieänderungen an der aktuellen Theorie
- g) Ändern der Theorie
Für dieses Experiment soll eine Neuinterpretation der Daten mit der bekannten allgemeinen Theorie über Induktion provoziert werden. Dies kann nach der Identifikation der Daten als anormale Daten z.B. durch die Leitfrage der Polentwicklung an der Spule geschehen. Das folgende GeoGebra Applet simuliert die Polentwicklung an der Spule, wobei hier eine Leiterschleife symbolisch für eine Spule mit N Windungen steht. (Bitte im Vollbildmodus benutzen)
Polentwicklung an einer Spule mit N Windungen
Weiter kann z.B. auch qualitativ über die Änderung des magnetischen Flusses in der Zeit argumentiert werden und versucht werden die Frequenz des Stabmagneten im Induktionsspannung-Diagramm wieder zu finden.
Ein weiterer interessanter Aspekt lieferte ein Selbstversuch von diesem Experiment. Die in diesem Selbstversuch gewonnenen Daten wurden schnell als anormale Daten identifiziert, aber nicht im Sinne von dem oben genannten Einsatz in einer Unterrichtsreihe, sondern im Sinne von "realen" anormalen Daten. Diese konnten zunächst nicht erklärt werden. Da aber die Theorie über Induktion sowie die abgeleitete Theorie für dieses Experiment als adäquat eingestuft werden kann, bleibt nach C. Chinn und W. Brewer nur das Ablehnen der Daten, d.h. beim Experimentieren muss ein Fehler vorgelegen haben.[4] Diese Einstufung erwies sich als adäquater Umgang mit den gewonnenen anormalen Daten, weil sich herausstellte, dass der benutzte Stabmagnet an einer Stelle gebrochen war. Das folgende GeoGebra Applet simuliert den Induktionsspannungsverlauf des funktionstüchtigen Stabmagneten und des gebrochenen Stabmagneten an der Spule, wobei hier wieder eine Leiterschleife symbolisch für eine Spule mit N Windungen steht. Weiter lassen sich in beiden Fällen die Magnetfeldlinien betrachten und somit auch qualitativ die beiden Verläufe verstehen. (Bitte im Vollbildmodus benutzen)
Induktionsspannungsverlauf eines funktionstüchtigen- und eines gebrochenen Stabmagneten an einer Spule mit N Windungen
Versuchsanleitung
Aufbau
Der Versuchsaufbau ist im Bild Aufbau dargestellt.
Der Motor wird in der Spannstelle des Stativfußes befestigt. An der Drehachse des Motors ist der Stabmagnet festgeschraubt. Unter dem Magnet wird die Spule z.B. 300 Windungen so angeordnet, dass die Drehachse des Motors genau mittig über der umgedrehten Spule (siehe Bild Aufbau) verläuft. Die Spule wird dann an das Messgerät mit zwei Kabeln angeschlossen. Der Motor wird als letztes an die Stromversorgung angeschlossen.[5] Dabei ist zu beachten, dass der rotierende Stabmagnet nicht die darunterlegende Spule treffen kann.
Für das Experiment wird benötigt:
- - 1x Voltkraft Digitaler Drehzahlmesser mit Laser DT1L, Firma Conrad Art.-Nr. Q038696
- - 1x MOBILE-CASSY 2, Firma Leybold Art.-Nr. 524005
- - 1x E-Motor Type 10:1 Getriebe, Firma PHYWE Art.-Nr. 11028-00
- - 3x Spulen 75W 300W 1200W, Firma PHYWE Art.-Nr. 06511-01; 06513-01; 06515-01
- - 1x Stabmagnet mit Aufsatz für einen E-Motor
- - 2x Verbindungskabel
- - 1x Stativmaterial
Durchführung
Der Lehrer oder die Schüler/innen stellen zunächst eine Umdrehungsfrequenz am Motor ein (z.B. 1000 U/min), die mit dem digitalen Drehzahlmesser festgehalten wird. Die nun induzierte Spannung in der Spule lässt man sich vom Mobile Cassy anzeigen und polten. (Einstellparameter beim Mobile Cassy: Messbereich: -0,1V bis 0,1V; Messzeit: 1s; Intervall: 1ms (1001 Werte); Trigger: an) Dann erstellt man zu mehreren weiteren Umdrehungsfrequenzen und unterschiedlichen Spulen Induktionsspannungsverläufe und wertet diese dann qualitativ aus.
Ergebnisse und qualitative Auswertung
Ergebnisse funktionstüchtiger Stabmagnet
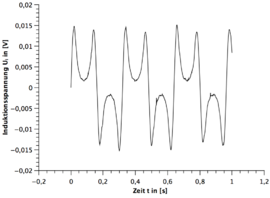
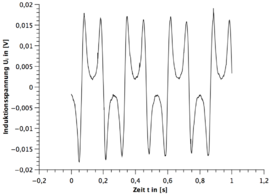
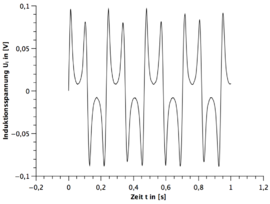
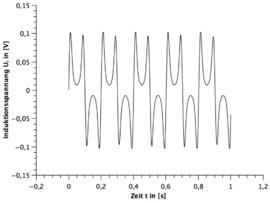
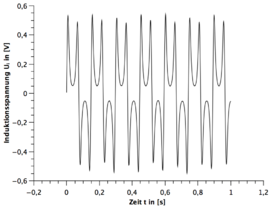
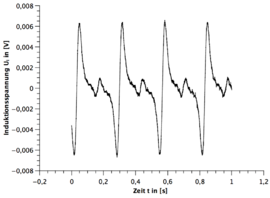
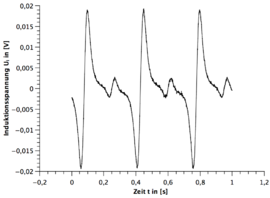
Alle Frequenzen des Stabmagneten sind mit dem Digitalen Drehzahlmesser gemessen worden. Die Messunsicherheit wurde immer auf geschätzt. Die Grafiken sind alle mit dem Program Qti-plot erstellt.
| Windung | 1.Frequenz | 2.Frequenz | 3.Frequenz |
|---|---|---|---|
| 75W | |||
| 300W | |||
| 1200W |
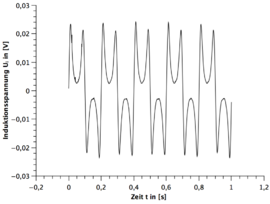
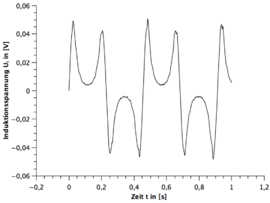
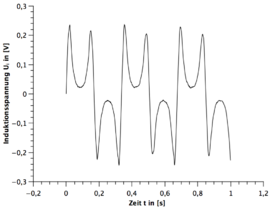
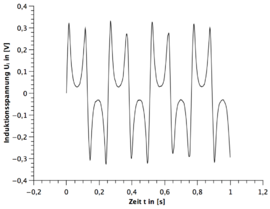
Ergebnisse gebrochener Stabmagnet
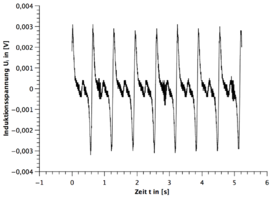
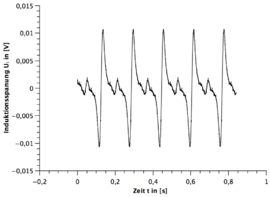
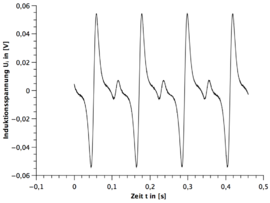
Alle Frequenzen des gebrochenen Stabmagneten sind mit dem digitalen Drehzahlmesser gemessen worden. Die Unsicherheit wurde wieder auf geschätzt. Dabei ist zu beachten, dass die Messzeit variiert.
| Windung | 1.Frequenz | 2.Frequenz | 3.Frequenz |
|---|---|---|---|
| 75W | |||
| 300W |
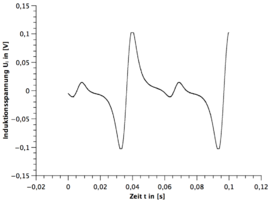
Qualitative Auswertung
- 1.) Eine Periode des Stabmagneten hat zwei sinusförmigen Perioden im Spannungsbild zur Folge. (siehe hierzu die beiden GeoGebra Applets)
- 2.) Die Zunahme der Umdrehungsfrequenz des Stabmagneten hat eine Zunahme bei der Amplitude des Spannungsverlaufes zur Folge.
- 3.) Je größer die Windung bei der Spule, desto größer die Spannungsamplitude bei gleicher Frequenz.
- 4.) Nach zwei sinusförmigen Perioden wiederholt sich das Spannungsbild.
- 5.) Bei dem funktionstüchtigen Stabmagneten ist immer die zweite sinusförmige Periode spiegelverkehrt zur ersten Periode und beim gebrochenen Stabmagneten nicht.
- 6.) Bei dem funktionstüchtigen Stabmagneten ist die Amplitude gleichbleibend und beim gebrochenen Stabmagneten existieren immer zwei verschiedene Amplituden die sich wiederholen.
- 7.) Bei dem funktionstüchtigen Stabmagneten geht die Induktionsspannung im Bereich des Übergangs von der ersten Periode zur zweiten gespielten Periode nicht auf null.
- 8.) Bei dem funktionstüchtigen Stabmagneten sind die beiden Amplituden der zwei gespiegelten Perioden nicht ganz identisch.
Den ersten und vierten Fakt kann man gut aus der Polbildung ableiten. Hierzu bietet sich das erste GeoGebra Applet an.
Die Zunahme der Amplitude des Spannungsverlaufes bei Zunahme der Umdrehungsfrequenz des Stabmagneten und der Einfluss der Windungszahl der Spule lässt sich aus der Formel der Induktion leicht ableiten.
Beim fünften und sechsten Fakt bietet sich das zweite Applet mit eingeschalteten Magnetfeldlinien an. Verfolgt man beide Verläufe so lässt sich der Spannungsverlauf gut qualitativ ableiten.
Der achte Fakt lässt sich mit der Trägheit des Systems erklären. In diesem Bereich kommt es zu einer Überlagerung der entgegengesetzten induzierten Spannungen und somit auch kein Abfall der Amplitude auf null.
Der letzte Fakt ist ein Resultat der asymmetrischen Rotation des Stabmagneten durch den E-Motor. Da die Amplitude mit unter von der Entfernung zu dem Stabmagneten zur Spule abhängt, muss eine asymmetrischen Rotation zwangsläufig zu unterschiedlichen Amplituden führen.
Sicherheitshinweise
Der rotierende Stabmagnet muss gut gesichert sein, da er sonst bei Rotation aus dem Gehäuse des Motors geschleudert werden kann. Weiter ist darauf zu achten, dass der Motor auf dem Stativfuß nicht anfängt sich aufzuschwingen und so dann vom Tisch fallen kann.
Literatur
- ↑ O. Georg: Elektrische Felder und Netzwerke. Berlin, 1999; S.343
- ↑ C. Chinn,W. Brewer, Review of Educational Research Spring 1993, Vol. 63, No. 1, pp. 1-49
- ↑ C. Chinn,W. Brewer, Review of Educational Research Spring 1993, Vol. 63, No. 1, pp. 39
- ↑ C. Chinn,W. Brewer, Review of Educational Research Spring 1993, Vol. 63, No. 1, pp. 6
- ↑ PHYWE-Schriftreihe: Physik in Demonstrationsversuchen A/B Elektrik II. Industrie-Druck GmbH, Verlag, Göttingen, E 7.1.6
Siehe auch
Hier können Sie auf andere Artikel im Wiki verweisen, die entweder Ihren Versuch anders darstellen oder thematisch sehr dicht an Ihren Artikel liegen. Fügen Sie dazu einfach einen internen Link ein.