Impulserhaltung (Luftkissenbahn)
| Impulserhaltung (Luftkissenbahn) | |
| Kurzbeschreibung | |
|---|---|
| Experiment zur Überprüfung der Impulserhaltung | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klassenstufe 7/8 |
| Basiskonzept: | Impuls, Kraftstoß |
| Sonstiges | |
| Durchführungsform | Demonstrationsexperiment, Gruppenversuch |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Daniel Kretschmer |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Tobias Ludwig |
Das nachfolgend beschriebene Experiment soll der Veranschaulichung von Stößen und der Impulserhaltung dienen. Die Luftkissenbahn bietet die Möglichkeit, Stöße verschiedener Art unter reibungsarmen Gegebenheiten durchzuführen und die Impulserhaltung im eindimensionalen Fall zu untersuchen. Sie zählt zu den Klassikern unter den Versuchsaufbauten im Bereich der Newtonschen Mechanik in der Schule. Die quantitative Betrachtung der Impulserhaltung kann sich - wie im Folgenden u.a. gezeigt wird - tückisch gestalten. Das Ziel dieses Beitrages ist es, in den folgenden Abschnitte Vorschläge und Tipps zur Anwendung der Luftkissenbahn im Unterricht zu geben.
Inhaltsverzeichnis
Fachliche Aspekte
Der Impuls ist eine grundlegende Größe in der Klassischen Mechanik. Nicht umsonst hält er Einzug in ihrer axiomatischen Formulierung nach Newton. Vor der Anwendung der Luftkissenbahn sollte der physikalische Stoß, der Kraftstoß, der Impuls und dessen Erhaltungssatz eingeführt worden sein. Ziel des Versuches soll es sein, die Impulserhaltung plausibel vorzuführen bzw. jene von den Schülerinnen und Schülern selbst überprüfen zu lassen. Für alle Nutzer seien nachstehend die versuchsrelevanten Zusammenhänge zum Thema Stoß behandelt:
Der Stoß
Der physikalische Stoß kann auf Grundlage verschiedener Kategorien charakterisiert werden. Zu jedem Experiment zur Untersuchung eines Stoßes muss die Art des beobachteten Stoßes im Vorfeld geklärt werden.
Der physikalische Stoß lässt sich in folgende Kategorien unterteilen:
- Freiheitsgrad des Stoßes
- Art des Stoßes
- Startimpulse der stoßenden Körper
Stöße erfolgen ein-, zwei- oder dreidimensional, sind entweder elastisch oder inelastisch und gestalten sich in Abhängigkeit der Massen und Startgeschwindigkeiten der stoßenden Körper verschieden.
Der Kraftstoß
Der Kraftstoß beschreibt die Impulsübertragung nach dem Wechselwirkungsprinzip. Selbst wenn die auftretenden Kräfte für den Beobachter während des Stoßprozesses zumeist nicht offensichtlich sind, muss eingesehen werden, dass einer Impulsänderung immer eine Kraft zugrundeliegt. Die gegenseitig wirkenden Kräfte der stoßenden Körper bedingen die wechselseitigen Impulsänderungen:
meint die von Körper 1 auf Körper 2 ausgeübte Kraft, entsprechend.
Impulserhaltung
Der Impuls eines Gesamtsystems ergibt sich als Summe aller einzubeziehenden Teilchenimpulse:
.
Gemäß Impulserhaltung ist der Gesamtimpuls vor dem Stoß gleich dem Gesamtimpuls nach dem Stoß und im Laufe der Zeit erhalten:
Elastischer und Inelastischer Stoß
Im Sinne der Energie- und Impulserhaltung ergeben sich die nützlichen, physikalischen Beziehungen:
Elastischer Stoß
Inelastischer Stoß
Didaktischer Teil
Stöße werden im Laufe des Berliner Rahmenlehrplans erstmalig im Pflichtbereich des Jahrgangs 7/8 im Themenfeld Mechanik eingeführt. Die Verwendung der Luftkissenbahn im Unterricht kann helfen, den Schülerinnen und Schülern Stoßvorgänge und das theoretische Konzept der Impulserhaltung experimentell näher zu bringen.
Schülervorstellungen
Wenn die Luftkissenbahn im Unterricht zur Anwendung kommt, sollte die Gelegenheit ergriffen werden, mit einigen möglichen Alltagsvorstellungen der Schülerinnen und Schüler zu Kraft und Impuls aufzuräumen. Nicht unüblich ist, dass Schülerinnen und Schüler den Begriff der Kraft übergeordnet auch anstelle des Impulses, einer Wirkung oder der Energie verwenden, sei es im Zuge ihrer Alltagssprache oder mangels einer fachlichen Einführung in die Konzepte von Kraft, Energie und Impuls. Die Kraft wird nicht nur als Ursache für die Veränderung von Bewegungsvorgängen gesehen, sondern auch als Eigenschaft des bewegten Körpers. Im vorliegenden Kontext ist die häufig anzutreffende Schülerfehlvorstellung besonders interessant, derer nach Körper, die sich gleichförmig bewegen, einer konstanten Kraft unterliegen, ohne die die Gleichförmigkeit der Bewegung nicht gegeben wäre. Diese Fehlvorstellung liegt in den alltäglichen Erfahrungen der Schülerinnen und Schüler begründet, in denen ihnen der entscheidene Einfluss der Reibung nicht bewusst ist. Die Luftkissenbahn kann dienen, der letztgenannten Fehlvorstellung entgegenzuwirken. Die reibungsarmen Versuchsbedingungen, die die Luftkissenbahn bietet, erlauben den Schülerinnen und Schüler die Einsicht, dass der Impuls, für die konstanten Massen der Gleiter genauer die Geschwindigkeiten, der sich bewegenden Gleiter gerade nur ohne Krafteinfluss erhalten bleiben. Zur Festigung dieser Erkenntnis sollte der Vergleich zu beschleunigten Gleitern gezogen werden, beispielsweise indem die Gleiter mit Massestücken an Fäden über Umlenkrollen beschleunigt werden (siehe auch Newtonsche Bewegungsgleichung)
Impuls als Vektor
Die Luftkissenbahn erlaubt lediglich die Betrachtung eindimensionaler Bewegungen. Diese Beschränkung auf eine Dimension kann als Vor- oder Nachteil der Luftkissenbahn gesehen werden. Einerseits ermöglicht die Eindimensionalität die Vernachlässigung des Vektorcharakters des Impulses, wodurch die mathematische Betrachtung der Impulserhaltung vereinfacht wird. Andererseits muss genau dieser vermeintliche Vorteil aus physikalischer Sicht auch als Nachteil aufgefasst werden. Für das Verständnis von Stoßvorgängen und der Impulserhaltung ist der Vektorcharakter des Impulses und das Verständnis der Vektorsumme essentiell. Damit ist zu erwarten, dass der mögliche Erkenntnisgewinn bzw. Zuwachs an Fachwissen an der Luftkissenbahn beschränkt ist.
Verwendung in der Schule
Der Umgang mit der Luftkissenbahn birgt mehrere potenzielle Lernmöglichkeiten für Schülerinnen und Schüler. Der Versuch erfordert an sich bereits, dass die Schülerinnen und Schüler den Umgang mit technischen Geräten üben, Messungen durchführen, diese auswerten und sich mit deren Unsicherheiten auseinandersetzen. Zur Klärung der Ergebnisse müssen die Schülerinnen und Schüler den Umgang mit dem Impulsbegriff lernen, die Erhaltung des Impulses wird als besonderer Sachverhalt erkannt. Wie oben angesprochen können alltägliche Fehlvorstellungen korrigiert werden. Es bedarf weiterer Unterrichtseinheiten, um das Wissen um die eindimensionale Impulserhaltung wie es an der Luftkissenbahn erworben werden kann zur verallgemeinerten Impulserhaltung im Dreidimensionalen zu erweitern.
Versuchsanleitung
Luftkissenbahn
Die Luftkissenbahn besteht aus einer metallenen Röhre mit kantigem Profil, welche vom dazugehörigen Gebläße durchströmt wird. Eine Vielzahl von kleinen Löchern ermöglicht, dass die Luft an der Oberseite der Bahn gerichtet austreten kann. Bahn- und Gleiterprofil müssen idealerweise zueinander passen. Wird ein Gleiter während des Betriebes auf die Bahn gesetzt, führt das entstandene Luftkissen dazu, dass die Reibung zwischen Gleiter und Bahn vernachlässigbar gering wird. Dadurch können sich Gleiter nahezu reibungsfrei über die Bahn bewegen. Für die Durchführung eines Stoßes ist es wichtig, die Luftkissenbahn waagerecht auszurichten. Dazu sind Stellschrauben an der Bahn angebracht. Für die grobe Voreinstellung kann eine Wasserwaage verwendet werden. Die Feinkorrekturen haben zum Ziel, dass sich der einzelne Gleiter bei Betrieb des Gebläßes zur Versuchsbeginn in Ruhe befindet. Mithilfe der Luftkissenbahn lassen sich elastische oder inelastische, eindimensionale bzw. frontale Stöße realisieren. Die Massen und Geschwindigkeiten der Gleiter sind variabel, aber im Rahmen der Durchführung durch die Maximalleistung des Bahngebläßes beschränkt. Ist die Masse eines Gleiters zu groß, kann sich über den Luftstrom kein Luftkissen unter ihm aufbauen, wodurch die Luftkissenbahn ihren grundlegenden Vorzug einbüßt. Reibungsarmes Gleiten über die Bahn ist dann nicht mehr gewährleistet.
Zubehör
- Luftkissenbahn mit Gebläse
- Gleiter
- Ringpuffer (elastischer Stoß)
- Kopplungsmagneten (inelastischer Stoß)
- 2 Lichtschranken (idealerweise aus dem CASSY-Zubehör)
- 2 Blenden
- CASSY-Modul
- CASSY Timer-Box
- CASSY-Lab-fähiger Rechner
- Spannungsquelle
Aufbau
Die Luftkissenbahn wird auf einer stabilen, möglichst waagerechten Unterlage aufgestellt. Das Gebläse wird angeschlossen. Die Lichtschranken werden so oberhalb der Bahn angebracht, dass die Gleiter in ihrer Bewegung nicht behindert werden und die auf den Gleitern aufgebrachten Blenden die Lichtschranken senkrecht durchlaufen. Auf das CASSY-Modul wird die Timer-Box aufgesetzt. Die Lichtschranken werden über die vorgesehenen Anschlüsse mit der Timer-Box verbunden. Das CASSY-Modul wird an einen Rechner angeschlossen.
Durchführung
- Das Gebläse der Luftkissenbahn wird eingeschaltet.
- Das Gebläse und die horizontale Ausrichtung der Luftkissenbahn werden so aufeinander abgestimmt, dass die Gleiter zu Versuchsbeginn in Ruhe sind.
- Die Gleiter werden je nach Stoßvariation relativ zu den Lichtschranken positioniert.
- Die Gleiter werden in Bewegung versetzt, die Messung erfolgt mithilfe von CASSY automatisch.
- Die Auswertung der aufgenommenen Daten erfolgt im Anschluss.
Elastischer Stoß
Zur Durchführung eines elastischen Stoßes werden die Gleiter von jeweils einem Ende der Luftkissenbahn gleichzeitig in Richtung des jeweils anderen Gleiters gestartet. Es ist sinnvoll, die zwei Lichtschranken um den Mittelpunkt der Bahn in einem ausreichend großen Abstand voneinander so zu positionieren, dass sie einen entsprechend großen Stoßbereich einrahmen. Die Anfangsimpulse der Gleiter müssen derart arrangiert werden, dass beide Gleiter die ihnen jeweils nächste Lichtschranke durchqueren und ihr Stoß innerhalb beider Schranken stattfindet. Nachdem sich die Bewegungsrichtung beider Gleiter umgekehrt hat, werden die resultierenden Impulse nach dem Stoß jeweils von derselben Lichtschranke vermessen. Sind die Impulse jedes Gleiters vor und nach dem Stoß erfasst worden, ist die Messung beendet. Die Elastizität des Stoßes wird durch die an einem Gleiter angebrachten Ring-Puffer (siehe Abb. 3) gewährleistet. Die Ring-Puffer ermöglichen eine nahezu verlustfreie Impulsübertragung. Notwendigerweise tragen beide Gleiter eine Blende.
Inelastischer Stoß
Zur Vermessung eines inelastischen Stoßes wird ein Gleiter in Ruhe zwischen den beiden Lichtschranken positioniert. Der zweite Gleiter wird von einem Ende der Luftkissenbahn in Richtung des ruhenden Gleiters in Bewegung versetzt. Die Positionen der Lichtschranken sind so zu wählen, dass nach der Messung des Startimpulses des zweiten Gleiters die Kopplung der beiden Gleiter erfolgen kann, bevor der resultierende gemeinsame Impuls durch die zweite Lichtschranke aufgenommen wird. Die Kopplung wird über einen Magneten und ein ferromagnetisches Gegenstück realisiert (siehe Abb. 4). Im Vergleich zum elastischen Stoß genügt es hier, nur den anfänglich in Bewegung versetzten Gleiter mit einer Blende zu versehen.
Messung mit CAS-System
CASSY[1] (Computer Assisted Science System) vom Hersteller LD-Didactic ist ein computerunterstütztes System für wissenschaftliche Anwendungen, das für Forschungs- aber auch für Lehrzwecke genutzt werden kann. Die Einarbeitung in die Software ist einmalig mit Zeitaufwand behaftet, aber die Nutzung einzelner Funktionen bedarf anschließend weniger Zeit. Die Software CASSY-Lab ermöglicht die übersichtliche Datenaufnahme und -auswertung nach Geschwindigkeit, Impuls und kinetischer Energie der verwendeten Gleiter. Für die Untersuchung der Impulserhaltung enthält die CASSY-Bedienungsanleitung das detaillierte Versuchsbeispiel "Impuls- und Energieerhaltung (Stoß)", das den hier diskutierten Versuch widergibt und dessen wesentliche Punkte hier aufgeführt sein sollen. Zu jedem im Handbuch beschriebenen Versuch bietet die CASSY-Software vorgefertigte Einstellungen, die über den "Werkzeugkasten" geladen werden können. Die vorgefertigten Messungseinstellungen für den Versuch "Impuls-und Energieerhaltung (Stoß)" eignen sich sehr gut für die Messung. Vor Versuchsbeginn sind die Massen der verwendeten Gleiter anzugeben. Beim inelastischen Stoß ist natürlich die resultierende Gesamtmasse beider Gleiter in Verbindung zu beachten. Ebenso einzugeben ist die Breite der aufgesetzten Blenden. Bei den folgend aufgeführten Messresultaten der Beispielmessung am inelastischen Stoß wurden die Massen der Gleiter auf Zehntelgramm, die Blendenlägen auf Millimeter genau bestimmt. Zuletzt ist unter vier Anordnungsmöglichkeiten für die Gleiter zu wählen, beide Gleiter außerhalb der Lichtschranken, nur der erste Gleiter innerhalb, etc. Zur Messung ist zu sagen, dass CASSY-Lab auf Grundlage der gemessenen Verdunklungszeiten der Lichtschranken auf die mittleren Geschwindigkeiten der Gleiter zurückschließt. Bei Messung über einen Eingang der Timer-Box gibt das Bedienerhandbuch eine Messtoleranz von 100 s an. CASSY-Lab bietet die Ausgabe der Verdunklungszeiten auf Millisekunden genau an. Im Vergleich zu den Toleranzen in den Massen der Gleiter und den Blendenbreiten ist die Zeitunsicherheit also vernachlässigbar. Die Betrachtung der Messunsicherheiten für Geschwindigkeit, Impuls und Energie wird durch die CASSY-Lab-Software nicht unterstützt. Eine ordentliche Unsicherheitenauswertung muss gesondert durchgeführt werden. Theoretisch reicht die Kenntnis der Massen, Blendenlängen und der Verdunklungszeiten zur Bestimmung der einzelnen Impulse. Die CASSY-Software bietet aber den großen Vorteil, dass keine Kalkulationsphase zwischen der Messung der Impulse und der Ausgabe der Messdaten eingeschoben werden muss. Anfangs- und Endimpuls des Systems sind praktisch instantan zur Messung sichtbar. Dadurch eignet sich die Zuhilfenahme der CASSY-Software im Unterricht besonders zu Demonstrationszwecken.
Auswertung
Messergebnisse
Anhand der Eingabedaten zu den Massen der Gleiter, den Längen der aufgesetzten Blenden und den Messdaten der Verdunklungszeiten errechnet CASSY-Lab den Impuls der Gleiter zu
.
Unter Maßgabe der verschiedenen Unsicherheiten ergibt sich die Impulsunsicherheit insgesamt als
.
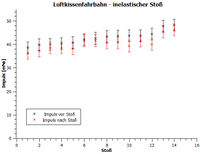
Bei der Beispielmessung am inelastischen Stoß wurden Gleiter der Massen und und einer Gesamtmasse von verwendet. Alle Angaben schließen die Kopplungsvorrichtungen mit ein. Der folgend angegebene Initialimpuls vor dem Stoß ist entsprechend dem inelastischen Stoß der Initialimpuls des anfangs gestarteten Gleiters. Die Blendenlänge betrug bei der Messung Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \Delta l=5cm} . Die Darstellung der Messdaten erfolgte mit QtiPlot[2]. Folgende Messdaten (vgl.s. Abb. 4) wurden bei der Beispielmessung aufgenommen:
| Stoß # | vor Stoß [mNs] | Unsicherheit [mNs] | nach Stoß [mNs] | Unsicherheit [mNs] |
|---|---|---|---|---|
| 1 | 38,6 | 2,5 | 36,3 | 2,4 |
| 2 | 39,9 | 2,5 | 37,2 | 2,4 |
| 3 | 40,1 | 2,5 | 38,6 | 2,5 |
| 4 | 40,4 | 2,5 | 38,6 | 2,5 |
| 5 | 40,8 | 2,5 | 38,2 | 2,4 |
| 6 | 42,1 | 2,6 | 40,7 | 2,5 |
| 7 | 42,6 | 2,6 | 41,6 | 2,6 |
| 8 | 43,4 | 2,6 | 40,6 | 2,5 |
| 9 | 43,5 | 2,6 | 40,7 | 2,5 |
| 10 | 43,7 | 2,6 | 39,3 | 2,5 |
| 11 | 43,7 | 2,6 | 41,5 | 2,6 |
| 12 | 44,4 | 2,6 | 40,1 | 2,5 |
| 13 | 47,8 | 2,7 | 45,4 | 2,7 |
| 14 | 48,3 | 2,7 | 46,2 | 2,7 |
Diskussion
Nach der Messung ist festzuhalten, dass die Impulserhaltung innerhalb der berechneten Toleranzen eingehalten wird, allerdings ist auffällig, dass der Gesamtimpuls nach dem Stoß systematisch unter dem anfänglichen Gesamtimpuls zurückbleibt. Es ist davon auszugehen, dass Reibungsquellen nicht erkannt und behoben wurden. Der Ursprung der systematischen Unsicherheit blieb nach der Messung ungeklärt, die Unsicherheit ist aber im Rahmen der ohnehin sehr geringen Einzelimpulse akzeptabel, jedoch für die Demonstration im Unterricht hinderlich, weil die auftretende Diskrepanz den Schülerinnen und Schülern mit zusätzlichem Aufwand nahegebracht werden muss. Einen überzeugenden Nachweis der Impulserhaltung aus didaktischer Sicht liefert die durchgeführte Messung leider nicht, zu viel Erklärung wäre im Ernstfall noch von Nöten. Unter der Bedingung, dass die offensichtlichen Verluste geklärt und beseitigt werden können, aber kann die Luftkissenbahn gute Dienste im Unterricht leisten.