Hitzedrahtampermeter
| Hitzedrahtampermeter | |
 Abbildung 1: Hitzedrahtampermeter als Eigenbau | |
| Kurzbeschreibung | |
|---|---|
| Hitzedrahtampermeter und quantitativer Zusammenhang von Stromstärke und Längenausdehnung | |
| Kategorien | |
| Elektrizitätslehre | |
| Einordnung in den Lehrplan | |
| Geeignet für: | 7/8 Klasse |
| Basiskonzept: | Materie |
| Sonstiges | |
| Durchführungsform | Demonstrationsexperiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | Oliver Baierl |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Dr. Franz Boczianowski |
Mit Hilfe eines Hitzedrahtampermeters lassen sich Stromstärken bestimmen. Dabei wird der Effekt ausgenutzt, dass beim Erhöhen der Stromstärke sich ein Draht erwärmt und sich dieser auf Grund dessen ausdehnt. In diesem Versuch soll der Zusammenhang von Stromstärke und Ausdehnung untersucht werden, sowie durch ein einfaches Hitzedrahtampermeter nachgebaut werden.
Inhaltsverzeichnis
Physikalische Vorbetrachtung
Ein elektrischer Leiter kann durch einen elektrischen Strom erwärmt werden. Der Draht dehnt sich aufgrund der Temperaturerhöhnung aus. Dabei ist die Stromstärke zum Quadrat proportional zur Längenausdehnung.
Für die elektrischen Leistung gilt:
Da der Konstatandraht, der in den Experimenten Anwendung gefunden hat, eine annähernd konstanten spezifischen Widerstand (siehe Quellen [1] Thyssenkrupp Seite 31) über eine hohen Temperaturbereich hat, folgt die Proportionalität von P und
Didaktischer Teil
Mit Hilfe des "Modellexperiment Hitzedrahtampermeter" können SuS mehre Physikalische Phänomene beobachten und auf ihrem bereits vorhanden Wissen Erklärungen geben. Die von den SuS beobachten Phänomene und deren Erklärungen, sowie deren Einbettung ins bereits vorhandene Wissengefüge soll im folgenden näher Betrachtet werden.
In der 7/8 Klasse im Modul "Vom inneren Aufbau der Materie" behandeln die SuS die Wärmelehre und erarbeiten den Zusammenhang zwischen Temperaturänderung und Längenänderung. Dieser Zusammenhang wird benötigt, um das Experiment erklären zu können. Ebenfalls in der Klassenstufe 7/8 wird das Modul P8 "Wirkungen bewegter Ladungen" behandelt. In diesem Unterrichtsabschnitt sollen die SuS den Zusammenhang von elektrischen Strom und Wärmewirkung erkennen und Anwendungsmöglichkeiten benennen können. Daher kann der Versuch gut als messtechnische Anwendungsbeispiel demonstriert werden. Damit der Versuch im Detail verstanden werden kann, ist es Sinnvoll diesen in Phasen bzw. Abschnitte zu gliedern und diese einzeln zu thematisieren .
In der ersten Phasen sollen die SuS die Erkenntnis gewinnen, dass durch einen stromdurchflossenen Leiter eine Wärmewirkung und somit in Folge dessen eine Temperaturerhöhung statt findet. Die Temperaturerhöhung ist dabei proportional zur elektrischen Leistung, welche durch eine Erhöhung der Stromstärke bei gleichbleibender Spannung, gesteigert werden kann.Das Glühen des Drahtes bei hohen Stromstärken kann dabei als Indikator für eine hohe Temperatur gewertet werden. Desweiteren sollte mit Hilfe des Teilchenmodells die Erhöhung der Temperatur erklärt werden. Fehlvorstellungen, die die Erklärung in der Begründung das die Elektronen, die sich nach einschalten des Stromes im Leiter befinden, auf Grund ihres Gewichtes den Draht dehnen, können dadurch vermieden werden.
In der zweiten Phase, in der die Längenänderung auf Grund der Temperaturänderung thematisiert werden soll, können die SuS ihr Wissen aus dem Modul „Vom inneren Aufbau der Materie“ anwenden und eine Erklärung für dieses Phänomen geben. Hierbei sollte auch nochmals kurz erklärt werden, dass die Längenänderung auf die Temperaturänderung zurückzuführen ist.
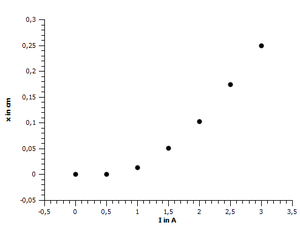
In Phase 3 soll der proportionale Zusammenhang von zu Längenausdehnung untersucht werden(Quantiative Überprüfung von Stromstärke und Längenausdehnung). Zur Einleitung der Phase kann man das Modellexperiment durchführen und eine Skaleneinteilung für bestimmte Stromstärken vornehmen. Dabei wird zu beobachten sein, dass die Einteilung anscheinend nicht linear sei. Die Überprüfung wird nach Anleitung zum quantitativen Experiment (Nachweis von ) mit den SuS gemeinsam durchgeführt. Wertet man die Ergebnisse aus, so erhält man die in Diagramm 1 abgebildeten Ergebnisse. Mit dem Diagramm 1 lässt sich die Vermutung bestätigen, dass kein linearer Zusammenhang zwischen der Stromstärke und der Längenausdehnung besteht. In der 8. Klasse wird im Mathematikunterricht bereits die quadratische Funktion behandelt, sodass leistungsstarke Schüler auf den Zusammenhang kommen können. Dieser Zusammenhang kann deutlich gemacht werden, indem die Skaleneinteilung bezüglich der Stromstärke quadriert wird, sodass wir eine lineare Abbildung(Abbildung 2) erhalten.
Kritische Betrachtung
Ein Problem stellt allerdings bei der Auswertung dar, dass die SuS im Mathematikunterricht noch nicht den Satz des Pythagoras in dieser Jahrgangstufe behandelt haben. Daher sollte an dieser Stelle mit Hilfe des Lehrers unter Einsatz von Excel oder ähnlichem die Unterrichtseinheit lehrerzentriert geleitet werden. Als Alternative lässt sich die Bestimmung des proportionalen Zusammenhanges auch durch eines vertikalen Aufbaus überprüfen. Dabei wird der Draht senkrecht am oberen Ende an eine Anschlussklemme befestigt und das untere Ende wird freischwingend an eine weitere freiehängende Klemme befestigt. Beide klemmen werden in Reihe mit einer Stromquelle verbunden. Da dieser Versuch von mir persönlich nicht durchgeführt wurde, kann ich keine weiteren Hinweise zum Versuch geben, sodass es dem Leser der Überprüfung selber überlassen ist.
Neben der Interpretation der beobachten Phänomene mit Hilfe des Teilchenmodell, eignet sich dieser Versuch vorallem um wissenschaftliches Arbeiten zu lehren und somit den Kompetenzbereich Erkenntnisgewinnung zu fördern.
Versuchsanleitung
Aufbau
Zwischen zwei Verteilerstützen wird ein ca. 80cm langer Konstantandraht gespannt. Der Konstantandrahtwird an eine Stromquelle angeschlossen. Dabei soll die Stromquelle einen Stromstärkebereich von ca 0-10A umfassen. Zur Durchführung des Versuches als Modellversuch wird wie folgt aufgebaut:
Hitzedrahtampermeter
In der Mitte des Drahtes wird eine Schnur befestigt, die über eine Role mit einem Gewicht bestückt ist. An der Rolle befestige man einen aus Papier bestehenden Pfeil. Mit diesem Versuch kann die Funktionsweise eines Hitzedrahtampermeters demonstriert werden.
Quantiative Überprüfung von Stromstärke und Längenausdehnung
Zur Durchführung der Veranschaulichung des quantitativen Zusammenhanges, wird die Konstruktion mit der Rolle entfernt und statt dessen eine Masse von 20g in die Mitte des Drahtes gehangen.
Durchführung
Hitzedrahtampermeter
Um das Modell Experiment durchzuführen erhöht man die Stromstärke schrittweise (0,2A) im Bereich von 0-2A.
Quantitative Überprüfung von Stromstärke und Längenausdehnung
Um die Abhängigkeit von Stromstärke und Ausdehnung zu untersuchen, erhöht man schrittweise die Stromstärke und misst die Differenz der Höhe zur Ruhe Lage. Dabei sollte man nach Einstellen der gewünschten Stromstärke dem System Zeit geben (ca.1 min) um sich auf eine Höhe einzupendeln. Die gemessene Höhe lässt sich nun benutzen, um die Ausdehnung des Drahtes zu berechnen(siehe Ergebnis und Auswertung).
Ergebnis und Auswertung
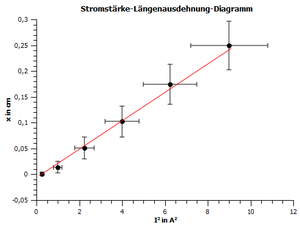
Bei der Untersuchung des quantitativen Zusammenhanges von Stromstärke und Längenaudehnung ergab sich folgender funktionaler Zusammenhang (siehe Abbildung 2)
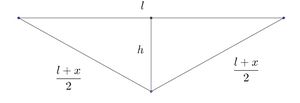
Dabei wurde eine Länge des Drahtes von 82cm gewählt sowie eine Masse von 20g verwendet. Die Stromstärke wurde schrittweise um 0,5A erhöht (0-3A). Dabei wurde die Höhe vier Mal gemessen und mit Hilfe des Satzes von Pythagoras die Längenänderung wie folgt ermittelt (siehe auch Abbildung 3):
Es gilt nach dem Satzes des Pythagoras:
Nach x aufgelöst folgt:
Da sein muss folgt:
Die Messunsicherheit des Ablesens der Höhe wurde mit 2mm abgeschätzt. Durch Fehlerfortpflanzung ergibt sich die Messunsicherheit wie folgt:
Die Messunsicherheit der Stromstärke wurde mit 0,1A abgeschätzt (1Skalenanteil). Aus der Fehlerfortpflanzung von lässt sich nun die Messunischerheit für die Stromstärke wie folgt bestimmen:
| Stromstärke I in A | Höhe h_1 | Höhe h_2 | Höhe h_3 | Höhe h_4 | Mittelwert Höhe in cm | Längenausdehnung in cm | u_x in cm | u_i in A |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0,5 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,001 | 0,003 | 0,18 |
| 1 | 0,7 | 0,8 | 0,7 | 0,8 | 0,75 | 0,014 | 0,011 | 0,34 |
| 1,5 | 1,4 | 1,5 | 1,5 | 1,4 | 1,45 | 0,05 | 0,021 | 0,48 |
| 2 | 2,1 | 2 | 2 | 2,1 | 2,05 | 0,10 | 0,029 | 0,56 |
| 2,5 | 2,8 | 2,6 | 2,6 | 2,7 | 2,68 | 0,17 | 0,039 | 0,65 |
| 3 | 3,2 | 3,2 | 3,2 | 3,2 | 3,2 | 0,25 | 0,048 | 0,71 |
Ergebniseinschätzung und kritische Betrachtung
Betrachtet man die in Abbildung 2 erhalten Messwerte, so liegen alle Werte innerhalb der Fehlerbalken auf einer Ursprungsgerade. Die Messunsicherheiten werden jedoch mit höherer Ausdehnung und Stromstärke hoch und weichen bis zu 20 Prozent vom Messwert ab. Um die Messunsicherheiten zu verkleinern, wäre es möglich den Versuch wie in Abschnitt "didaktischen Teil- kritische Betrachtung" zu varieriern und eine vertikale Anordnung vorzunehmen.
Sicherheitshinweise
Da der Konstantandraht hohe Temperaturen erreicht, sollte der Versuch durch eine Lehrkraft durchgeführt werden. Auch ist es sinnvoll unterhalb des Drahtes den Tisch mit Alufolie oder ähnlichem zu schützen. Bei zu hohen Stromstärken, kann es zum Reißen des Drahtes kommen, sodass dieser Brandstellen am Tisch verursachen kann.
Literatur
- http://www.thyssenkrupp-vdm.com/fileadmin/Downloads/Broschueren/pdf/Draht-Elektroindustrie_de+en.pdf