Gummiband-Kraftmesser

Gummiband-Kraftmesser
Ein selbstgebauter Kraftmesser
Kurzbeschreibung
Aufbereitung von Messwerten (linearer Fit)
Kategorien
Unterrichtsmaterialien, Messunsicherheiten
Einordnung in den Lehrplan
Geeignet für:	Sek. I & II
Basiskonzept:	-
Sonstiges
Durchführungsform	Gruppenexperiment
Anzahl Experimente in dieser Unterkategorie	1
Anspruch des Aufbaus	einfach
Informationen
Name:	F. Boczianowski, L. Pyras
Kontakt:	franz.boczianowski@physik.hu-berlin.de
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	-

Es wird den Lernenden zur Aufgabe gemacht, aus einem Lineal, einem Gummiband und etwas Tesafilm einen Kraftmesser bauen. Zur Kalibration dient ein kommerzieller Kraftmesser. Das Ziel ist es, dass die Lernenden für ihren eigenen Kraftmesser eine Umrechnungsformel $f(x)=a\cdot x+b$ entwickeln, mit der die Ausdehnung des Gummibandes (gemessen in cm) direkt in die Kraft (in Newton) umgerechnet werden kann. Insbesondere der Umrechnungsfaktor $a$ ist aus der Steigung des linearen Fits zu bestimmen.

Didaktische Anmerkung

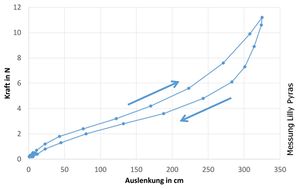
Ein Gummiband verhält sich nur über einem kleinen Bereich linear (siehe Messung unten). Gerade deswegen eignet sich dieses Experiment, zur Thematisierung linearer Ausgleichsgraden. In welchen Bereichen ist eine linearer Fit angemessen? Wo sind die Grenzen des linearen Modells? Wie sind Messunsicherheiten zu berücksichtigen?

Geräte

Für 23 Stationen:

• 23 Lineal
• 100 Gummibänder
• 23 Tesafilmrollen
• 23 Kraftmesser, vorzugsweise aus dem Bereich 5N bis 10N, zur Not 3N
• alternativ: Küchenwaagen

Aufgabenstellung

Bauen Sie nur aus Gummibändern, einem Lineal und Klebeband einen Kraftmesser! Verwenden Sie zur Kalibrierung einen kommerziellen Kraftmesser. Es ist für das weitere Vorgehen hilfreich, Messwerte der Kalibrierung in ein Kraft-über-Weg-Diagramm einzutragen und einen linearen Fit händisch einzuzeichnen (Hellwig (2012): Konzept Einsatz von Ausgleichsgeraden. Kapitel 9.4.3, Seite 185 ). Geben Sie eine Umrechnungsformel in der Gestallt $f(x)=a\cdot x+b$ an, mit der ein Skalenwert des Lineals (in Zentimeter) in eine Kraft (in Newton) umgerechnet werden kann. Benennen Sie die Unsicherheit Ihres Kalibrierungsfaktors $a$ und Ihres Achsenabschnitts $b$ anhand des Diagramms.

Anmerkung für die Lehrperson

Hypothese

Den Lernenden wird die Hypothese vorgegeben: "Das Gummiband dehnt sich linear mit der angreifenden Kraft aus."

Durchführung

• Das Gummiband mit Tesa des Lineals befestigen, siehe Abb. Dabei ist darauf zu achten, dass das Gummiband möglichst nah an der Ecke befestigt wird, um Auslenkungen möglichst entlang zur Skala zu garantieren.
• Bei der Messung die Auslenkung variieren und die Kraft ablesen.
• Je nach vorhandenem Kraftmesser müssen die Gummis auch doppelt oder dreifach genommen werden, siehe Abb.
• Bei der Verwendung einer Küchenwaage anstelle eines Kraftmessers ist ein schweres Objekt mit Bindfaden auf die Waage zu legen, z.B. Tetrapack, Wasserflasche. Dann die Waage auf Null setzen.

Kalibration des Eigenbaukraftmessers

Messunsicherheiten

Die Messunsicherheit ist durch viele Faktoren bestimmt, z. B. Ablesegenauigkeit am Kraftmesser bzw. Lineal, Reibung im und am Kraftmesser. Von weit größerem Einfluss ist jedoch die Hysterese des Gummibandes. Die Unsicherheit der Auslenkung $x$ wurde mit $u_{x}=$ 1 cm abgeschätzt. Auch die Ruhelage des y-Achsenabschnitts $b$ in Umrechnungsformel $f(x)=a\cdot x+b$ verschiebt sich um bis zu 2 cm.

Auswertung

Für den unteren Bereich der Kennlinie ist ein linearer Fit möglich. Für größere Kräfte ist unter Umständen ein zweiter linearer Fit funktional, um auch hier eine Verwendungen des Eigenbau-Kraftmessers zu ermöglichen.

Lösungsvorschlag

Kraft F [N]	Zentimeterskala x* [cm]	Auslenkung x [cm]
0	6.8	0
0.25	8.2	1.4
0.5	9.7	2.9
0.75	11.5	4.7
1	13.9	7.1
1.25	16.6	9.8
1.5	18	11.2
1.75	20.4	13.6
2	21.2	14.4
2.25	21.9	15.1
2.5	22.4	15.6
2.75	23	16.2
3	23.7	16.9
3.25	24.2	17.4
3.5	24.7	17.9
3.75	25.1	18.3
4	25.6	18.8
4.25	26	19.2
4.5	26.4	19.6
4.75	26.7	19.9
5	27.1	20.3

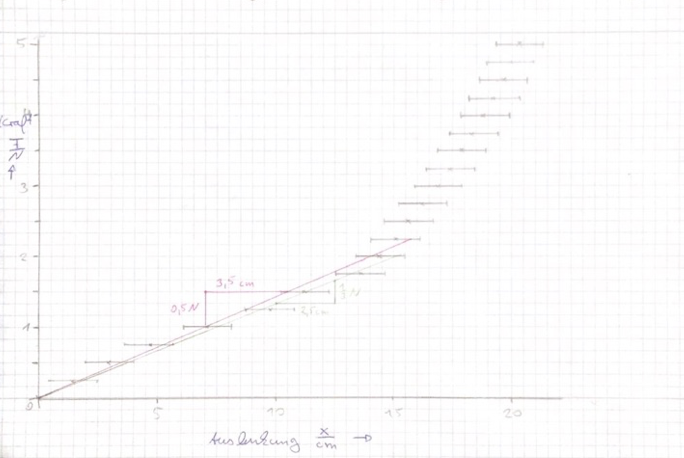
Die Werte werden in ein Diagramm, siehe unten, eingetragen und ein händischer linearer Plot erstellt (nach Hellwig Kapitel 9.4.3., Seite 185 ff ^[1]). Für den linearen Fit wurden nur die Werte bis einschließlich 1,5 N berücksichtigt.

(Messung Stephen Mayer)

• Die Steigungen der zwei Extremgeraden beträgt $a_{1}={\frac {0,5N}{3,5cm}}$ bzw. $a_{2}={\frac {{\frac {1}{3}}N}{2,5cm}}$.
• Als Mittelwert ergibt sich demnach $a=(29\pm 1)\cdot {\frac {1}{210}}{\frac {N}{cm}}$.

Variante Demonstrationexperiment

Gummiband zwischen Kraftmesser und Wegaufnehmer eines digitalen Messwerterfassungssystems

Hysterese eines Gummibandes

Literatur

,,