Frequenz und Wellenlängen einer Flöte
| Frequenz und Wellenlängen einer Flöte | |
 Messung eines Audiospektrums mit Phyphox | |
| Kurzbeschreibung | |
|---|---|
| Mit der Smartphone-App Phyphox lassen sich einfach Frequenzmessungen, z. B. an Flöten durchführen. | |
| Kategorien | |
| Unterrichtsmaterialien, Digitales Messen,Messunsicherheiten, Experimente für zu Hause | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | F. Boczianowski, L. Pyras |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
Inhaltsverzeichnis
Didaktische Anmerkung
Geräte
Für eine Station:
- Phyphox (auf dem Smartphone)
- Röhren mit einem verschlossenen Ende(4 Röhren, Durchmesser 16mm)
- Lineal
Aufgabenstellung
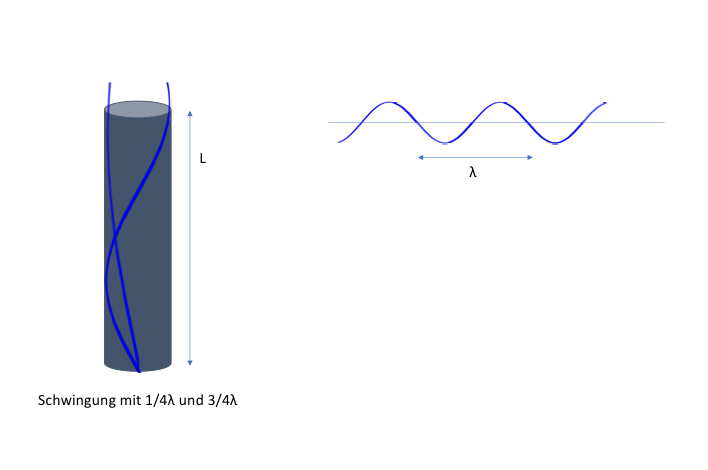
Mit Hilfe von verschiedenen Röhren mit je einem offenen und einem geschlossenen Ende kann ein hörbarer Ton erzeugt werden, der sich mit Schallgeschwindigkeit ausbreitet. Dazu wird das Rohr angeblasen und so eine stehende Welle erzeugt. Das Frequenzspektrum lässt sich mit einer App auf dem Smartphone messen.
Forschungsfrage:
Lässt sich die stehende akustische Welle durch eine Sinusfunktion des Drucks mit den folgenden Randbedingungen modellieren: Bauch am geschlossenen Ende und Knoten an der Öffnung des Rohres?
Zum Vergleich der Literaturwert: c = 343 m/s bei 20 °C
Hypothese:
Die Wellenlänge des Grundtons entspricht dem Vierfachen der Länge der Flöte.
Durchführung
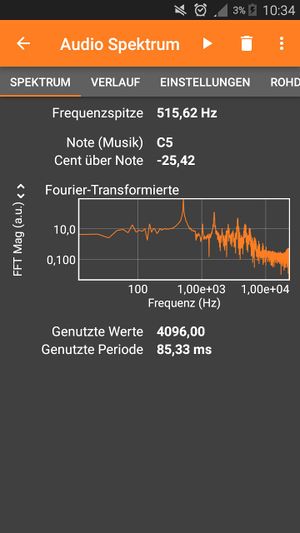
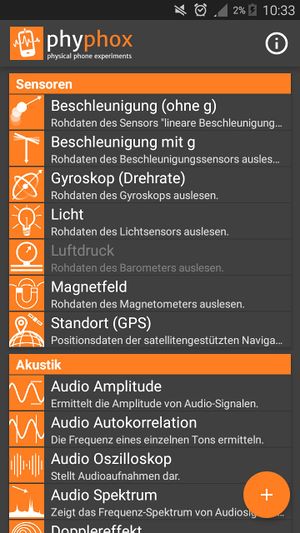
a) Zur Bestimmung der Frequenz können Sie die App Phyphox verwenden. Wählen Sie dafür im Menü Audio Spektrum aus.
b) Bestimmen Sie die Frequenzen der unterschiedlichen Röhren und schätzen Sie den Fehler ab.
c) Speichern Sie zusätzlich pro Rohr ein ausgewähltes akustisches Spektrum (Klick in phyphox auf drei Punkte oben rechts, "Daten exportieren", Format: CVS, "Teilen" an Mail-App und verschicken). Plotten Sie das Spektrum mit QTI (im Anschluss im PC Pool).
Auswertung
d) Erstellen Sie zur Prüfung der Hypothese ein geeignetes Diagramm mit linearem Fit mit QTI (im Anschluss im PC Pool).
Schluss:
e) Lässt sich die Hypothese stützen? Berücksichtigen Sie dabei die Messunsicherheiten.
Ziehen Sie einen Schluss und machen Sie Vorschläge für weitere Untersuchungen.
Hinweise/Hilfe
- Die Stud. sollen möglichst selbst auf die Idee kommen, dass sich der Fehler nur durch die Wiederholung der Messung abschätzen lässt. Also (bewusste oder unbewusste) Variation des Anblasens. Beispielsweise sechs Messwerte pro Röhrchen
- Ein zur Hypothese geeignetes Diagramm stellt die Welllänge über der Rohrlänge dar.
- Die Steigung für den Grundton beträgt ≈4. Es gibt u. U. einen Offset (Y-Achsen-Abschnitt) Das Rohr ist kürzer als ein Viertel der Wellenlänge.
- Knoten und Bäuche liegen für die Geschwindigkeit der Luft an umgekehrten Stellen.
- Die Wellenlänge lässt sich aus der Division von Geschwindigkeit der sich ausbreitenden Schallwellen durch die Frequenz bestimmen (c=λ∙f).
- Die stehenden Wellen der höheren Moden (Obertöne) führen zu den weiteren Frequenzspitzen.
Handhandhabung Phyphox
- In Phyphox: Auswahl Audiospektrum
- Aufnahme wird durch Drücken auf Play-Taste gestartet
- Das aktuelle Frequenzspektrum ist in einem Diagramm dargestellt
- Röhre wird angeblasen
Anmerkungen: Werden die Röhren stark angeblasen, ergeben sich „passendere“ Werte. Die Studenten sind nicht sofort darauf hinzuweisen. Ergebnisse sind in jedem Fall legitim. Je nach Durchführung können die Werte also unterschiedlich stark streuen, bzw. abweichen.
- Spitzen sollten im Diagramm zu erkennen sein
- Erfassung aktuellen Messwerte durch Klicken auf Pause-Taste
- Frequenzspitze wird über dem Diagramm angezeigt
- Y-Achse des Diagrammes zeigt die Intensität der jeweiligen Frequenz an
- beide Achsen sind logarithmisch aufgetragen (erleichtert die Unterscheidung zwischen Peaks und Hintergrundrauschen)
- Frequenz des höchsten Peaks und Grundton werden angezeigt
- Daten können durch Klicken auf erweiterte Optionen (drei Punkte oben rechts) exportiert werden. Für QTI am besten: CVS.
Messunsicherheiten
- Jede Röhre sollte mehrmals angeblasen und die Spitzenfrequenz notiert werden.
Anmerkungen: Es hat sich bewährt, 6 Messungen pro Rohr durchzuführen. Die Studierenden sollen die Notwendigkeit der Messwiederholung selbst erkennen.
- Die Abschätzung der Unsicherheit erfolgt nach der Größtfehlermethode, d.h. die Messunsicherheit entspricht der halben Differenz aus größter und kleinster Frequenz.
Auswertung
Wellenlänge bestimmen
- Aus der Theorie heraus entspricht in erster Näherung die Rohrlänge einem Viertel der Wellenlänge. (Das ist die Hypothese des Experiments!)
- λ=4∙L/n. Der Faktor n entspricht der Mode. Für eine Röhre mit einem offenen und einem geschlossenen Ende ist n=1,3,5,…. Wir betrachten nur n=1
- In einem Wellenlänge-Rohrlängen-Diagramm ist ein linearer Fit zu erstellen. Steigung a=4 ist erkennbar.
- Die Steigung für den Grundton beträgt ≈4. Es gibt u. U. einen Offset (y-Achsen-Abschnitt): Das Rohr ist kürzer als ein Viertel der Wellenlänge. Es gibt eine Korrektur ∆L. Daraus folgt: λ=4∙(L+∆L).
Schlussfolgerung
- Im Fall von geringer Varianz der Tonhöhen (immer gleiches Anblasen) ist dieser Effekt signifikant und die Hypothese zu verwerfen. Anderenfalls wird sie (schwach) gestützt.
Weitere mögliche Untersuchung:
- Der Bauch der stehenden Welle befindet sich etwas über der Röhre.
Ursachen:
- Die stehende Welle endet nicht schlagartig. Die Lage des Punktes für den Normaldruck liegt in leichter Entfernung zum Rohr (Viskosität)
- Der erzeugte Luftwirbel liegt durch das Anblasen vermutlich über dem Rohr.
- Die Länge der Röhre lässt sich wie folgt korrigieren L'=L+∆L
mit L = Länge der Röhre und ∆L = Korrektur, effektiven Länge L'. Nach Ruiz 2014 gilt: ∆L=0,6∙r mit r = Radius der Röhre. Der Wert 0,6 ist theoretisch vorhergesagt und experimentell bestimmt wurden.
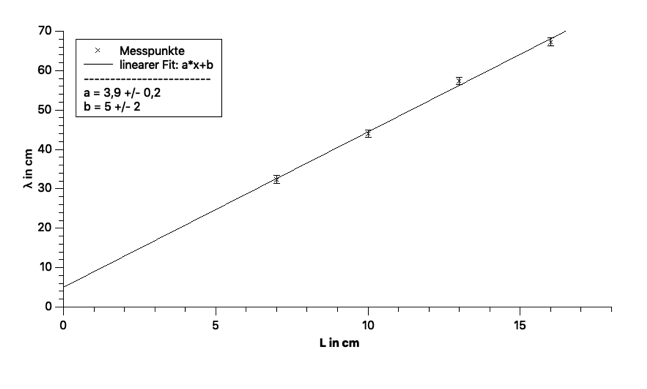
Abb. 1: Messwerte der Frequenz umgerechnet in die Wellenlänge dargestellt in Abhängigkeit der Rohrlänge.
Zusatzaufgabe: Frequenzspektrum darstellen
- Export und die Darstellung der Daten als Diagramm in z.B. Qti
- hier logarithmische Achsen verwenden, um die Spitzen für höhere Moden besser sichtbar zu machen
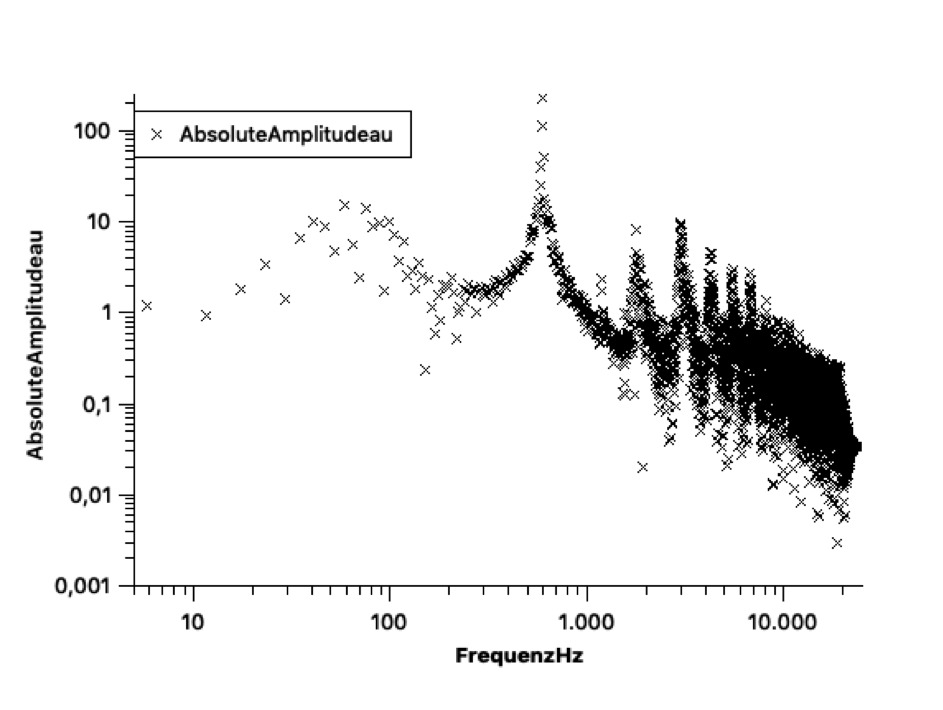
Abb. 2:13 cm lange Röhre mit 1,6 cm Durchmesser.
Daten
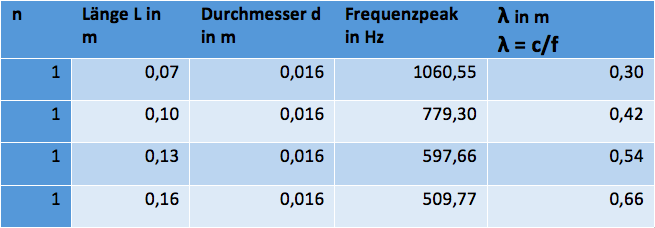
Tab. 1:Mehrere Röhren in verschiedenen Längen. Der Frequenzpeak wird in Phyphox abgelesen. λ kann anschließend aus der Schallgeschwindigkeit berechnet werden.
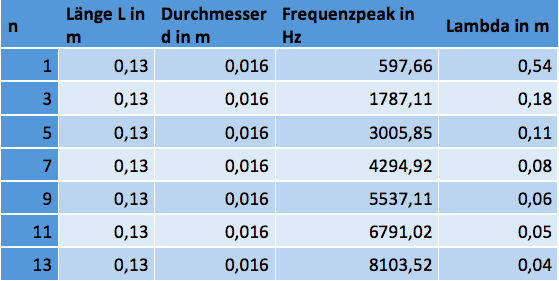
Tab. 2:Eine Röhre mit verschiedenen Moden. Nicht von den Studierenden zu erstellen.
Datei für den 3D Drucker
In dem Ordner befinden sich .stl Dateien für Röhren mit den Außendurchmessern von 16mm, 17mm und 20mm.
Zudem gibt es ein Beispiel Code für das Programm OpenScad. Dort können weitere Durchmesser eingegeben werden.
durchmesser = 17 ; // hier den Außendurchmesser des Rohres in mm eingeben
cylinder(h=1,d=durchmesser+2,center=true, $fn = 100); // Bodenplatte
difference() {
translate([0,0,5]){
cylinder(h=10,d=durchmesser+1,center=true, $fn = 100); //Außenschale
}
translate([0,0,5]){
cylinder(h=11,d=durchmesser,center=true, $fn = 100); //Innenschale
}
}
Literatur
Ruiz: “The end correction is due to the fact that the pressure nodes are outside the pipe, extending the pipe length by approximately 0.6r for each open end, where r is the inner radius of the pipe.” Raichel: “The assumption that ZnL = 0 at x = L (which would lead to resonances at f_n= 1⁄2 nc/L ) is not valid, because the open end of the pipe radiates into the surrounding air. […] Also, the presence of a flange at the open end affects the exit impedance. (https://www.arauacustica.com/files/publicaciones_relacionados/pdf_esp_198.pdf, S. 134)
 Dies ist die
Dies ist die