Franck-Hertz-Versuch mit Hg (Quecksilber)
| Franck-Hertz-Versuch mit Hg (Quecksilber) | |
 Aufbau des F-H-V | |
| Kurzbeschreibung | |
|---|---|
| Der Franck-Hertz-Versuch zeigt ein dominantes Anregungsniveau von Quecksilber. | |
| Kategorien | |
| Atom- und Kernphysik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Materie, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | leicht - mittelschwer |
| Informationen | |
| Name: | Maximilian Galensa |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Steffen Wagner |
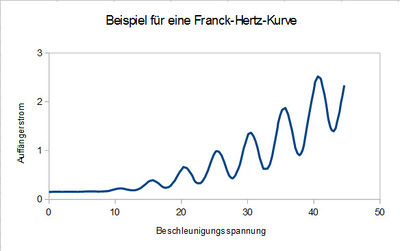
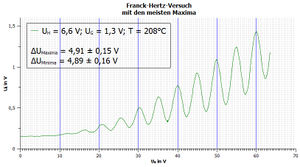
Der Franck-Hertz-Versuch mit Quecksilberdampf ist ein wichtiger historischer Versuch, der anschaulich zeigt, dass Atome Quanteneigenschaften in Form wohl definierter Energieniveaus haben. Für den Versuch werden Elektronen mithilfe eines elektrischen Feldes in Quecksilberdampf beschleunigt. Der Auffängerstrom wird in Abhängigkeit von der Beschleunigungsspannung gemessen und zeigt die eine periodische Kurve, die als Franck-Hertz-Kurve bezeichnet wird (siehe Abb.1). Aus dem Abstand der Maxima oder Minima lässt sich die zweite Anregungsenergie von Quecksilber 4,89 eV bis auf 0,2 eV genau bestimmen.
Inhaltsverzeichnis
Didaktischer Teil
Trotz der großen Popularität und historischen Relevanz des Versuchs stellen gängige Lehrbücher, wie der hier verwendete Gesamtband Physik für die Oberstufe von Cornelsen, nicht alle möglichen Beobachtungen des Experiments dar und vernachlässigen einige Punkte, die für das Verständnis der Vorgänge innerhalb der Röhre wichtig sind. [1]
Es entstehen deutlich sichtbare Leuchterscheinungen in der Röhre, die im Lehrbuch nicht diskutiert werden. (Vgl. Abb 2) Auch das für das Experiment bezeichnende und die Arbeit am meisten beeinflussende Phänomen des „Zünden“ des Gases wird im Lehrbuch ignoriert. Des Weiteren scheint es dort, als hätte Quecksilber sein erstes Anregungsniveau bei 4,9 eV, obwohl dieser Wert dem zweiten Energieniveau (Übergang 61S0 → 63P1) entspricht. Das erste Energienivau bei 4,67 eV (Übergang 61S0 → 63P0) wird nicht angesprochen. Letztendlich riskiert diese Lehrbuchinterpretation die Fehlvorstellung, die Elektronen würden sich näherungsweise geradlinig auf einer ausgezeichneten Z-Achse in der Röhre bewegen (Vgl. Abb 3), was mitnichten der Fall ist und geklärt werden sollte. Auch eine etwas genauere Untersuchung der Energieunterschiede zwischen den Elektronen unterstützt das umfassende Verständnis der Vorgänge während des Versuchs. [2]
Zur Erklärung der Leuchterscheinungen wäre es sinnvoll, sich das Licht einer Quecksilberdampflampe anzusehen und die sichtbaren Frequenzen (die Farbe) der beiden Lichtquellen zu vergleichen. Das Lehrbuch berichtet, dass Franck und Hertz die zugehörige Spektrallinie zu 4,9 eV (bei 254nm, nicht sichtbar) nachweisen konnten. Tatsächlich lässt sich mithilfe eines Fotomultipliers im Rahmen eines leicht abgeänderten Versuchs sogar nachweisen, dass das Licht dieser Frequenz stufenweise mit jedem neuen Maximum ansteigt. [3] Der Multiplier ist wichtig, da es schwer bis unmöglich ist, ein USB-Spektroskop auf die Leuchterscheinung in der Röhre auszurichten.
Das Phänomen des „Zünden des Gases“ kann den SuS mithilfe einer Unterrichtsphase zur Gasentladung nahegebracht werden. Eine kurze Thematisierung metastabiler Zustände kann erklären, warum Quecksilber auf das zweite Anregungsniveau angeregt wird, statt auf das erste. Eine Betrachtung der Streuquerschnitte und ihre Interpretation als Stoßwahrscheinlichkeiten zeigt, warum sich die Elektronen als nahezu isotroper Schwarm bewegen und nicht etwa als Strahl. Die vielen elastischen Stöße sind neben der Austrittsenergie aus der Katode ebenso ein weiterer Faktor für die breite Energieverteilung der Elektronen. [4]
Versuchsanleitung
Aufbau
Folgende Geräte und Materialien wurden für den Versuchaufbau genutzt:
- Frank-Hertz-Betriebsgerät (Elwe)
- Frank-Hertz-Röhe (Neva)
- Ofen für Frank-Hertz-Versuch mit Hg (Neva)
- Thermometer (Peaktech)
- Messfühler NiCr-Ni – Typ K, Messbereich -65°C – +1000°C (Greisinger)
- 2 Multimeter (Peaktech)
- Laptop mit Cassy (Leyboldt)
- gr. Cassy-Sensor mit zwei Spannungseingängen (Leyboldt)
- Experimentierkabel
- Schutzhandschuhe
Die Ausgänge an Betriebsgerät und der Platte, an der die Röhre befestigt ist, sind mit den Buchstaben A (für Acceleration), K (für Katode) und H (für Heizung) versehen, sodass die Verbindung zwischen Röhre und Betriebsgerät sehr einfach herzustellen ist.
Der erste Spannungseingang des Cassy-Sensors wird mit dem Output (FH Signal) und der zugehörigen Erde verbunden. Der zweite mit dem Eingang für die Beschleunigungsspannung und der Katode. Der Sensor wird via mitgeliefertem USB-Kabel an den Laptop angeschlossen. Das Programm wird so eingestellt, dass der erste Spannungseingang auf der y-Achse und der zweite auf der x-Achse abgebildet wird. Es ist außerdem nützlich, sich die Signalstärken anzeigen zu lassen. Ein Offset in y-Richtung ist normal und ergibt sich aus der Internen Spannung des Betriebsgeräts. Ein sinnvoller Messbereich ist 0-2 V auf der y-Achse und 0-80 V auf der x-Achse.
Die Multimeter werden auf Spannungsmessung eingestellt. Die Heizspannung kann zwischen dem Eingang für die Heizung am Betriebsgerät und der Katode gemessen werden. Der Anfangswert für die Gegenspannung zwischen dem Output (FH Signal) und dem Eingang der Beschleunigungsspannung an der Röhre. Dieses Multimeter sollte vor dem Aufdrehen der Beschleunigungsspannung entfernt werden, um Schäden am Verstärker des Betriebsgeräts zu vermeiden. Der Messfühler wird an das Thermometer angeschlossen und in die vorgesehene Öffnung im Ofen eingeführt.
Ofen, Betriebsgerät und Cassy-Sensor werden mit dem Stromnetz verbunden.
Durchführung
Der Ofen wird eingeschaltet und auf 190-200 °C eingestellt. Das Erreichen der Betriebstemperatur kann je nach Ofen bis zu 20 Minuten dauern, es ist also ratsam diesen Schritt als erstes durchzuführen. Will man den Ofen später bewegen, sind Schutzhandschuhe anzulegen.
Es ist darauf zu achten, dass Beschleunigungsspannung und Heizspannung am Betriebsgerät auf 0 V stehen und der Ofen nicht kälter als 150 °C ist. Das Betriebsgerät und der Cassy-Sensor werden eingeschaltet. Die Heizspannung wird auf ca. 6,5 V eingestellt. Die Amplitude des Verstärkers wird beinahe auf das Maximum eingestellt.
Die Messung mit Cassy wird gestartet. Langsam und gleichmäßig wird die Beschleunigungsspannung hochgedreht. Bei einem sofortigen, starken Spannungsanstieg, ist sofort die Messung zu beenden und die Beschleunigungsspannung zurück auf 0 V zu drehen, da das Gas gezündet hat und die Röhre zu schonen ist.
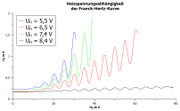
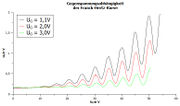
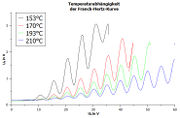
Zur Optimierung der Kurve können Heiz- und Gegenspannung, sowie Ofentemperatur genutzt werden. (Vgl. Abb. 4-6) Es ist völlig normal, nicht sofort eine Kurve zu sehen, bevor das Gas zündet. Ob es gezündet hat, lässt sich an einem relativ starken quecksilber-typischen türkisen Leuchten im Inneren der Röhre an der Katode beobachten.
Zum Ablesen der Energiedifferenzen werden die Abstände der Maxima oder Minima in der Cassy-Tabelle, die nach der Versuchsdurchführung aus dem Programm in ein beliebiges Tabellenkalkulationsprogramm hineinkopiert werden kann, gesucht und der kleinere Wert vom größeren Abgezogen. Eine Mittelwertbildung der Ergebnisse für die Abstände zwischen den Maxima und Minima ist sinnvoll, um ein gewichtetes Ergebnis für die zweite Anregungsenergie von Quecksilber zu bekommen.
Ergebnisse
Die Kurve erscheint um ca. 0,16 V in y-Richtung versetzt. Der Abstand der Maxima, wie der Minima ergibt in etwa (4,9 ± 0,15) eV. Die Werte (Vgl. Abb. 7) wurden mithilfe von Mittelwert und Standardabweichung aus den Messergebnissen (siehe Tabellen weiter unten) ermittelt. Es handelt sich um eine zufällige Messunsicherheit. Die systematische Messunsicherheit, die sich aus den anderen angeregten Energienivaus und den elastischen Stößen der Elektronen mit den Quecksilberatomen ergibt, lässt sich aufgrund ihrer Komplexität nicht herausrechnen, ist aber klein genug, um im Rahmen der zufälligen Messunsicherheit vernachlässigt zu werden. Die Kurve entspricht keiner strengen Sägezahnstruktur, sondern die Franck-Hertz-Kurve ist gekrümmt und die Werte des Auffängerstroms für Maxima, wie Minima steigen.
Die erste Andeutung eines Maximums zeigt sich bei etwa 13 eV, das erste deutlich ablesbare Maximum liegt bei etwa 21 eV, das letzte etwa bei 60 eV. Insgesamt sind elf Maxima und zehn Minima zu erkenen, von denen jeweils neun Maxima und Minima gut genug zu erkennen waren, um in die Rechnung einzugehen. Die Maxima, wie die Minima entstehen mit zunehmender Anzahl bei immer höheren Werten für den Anodenstrom. (Vgl. Abb. 7)
Bei einer von Heizspannung, Temperatur und Gegenspannung abhängigen Beschleunigungspannung zündet das Gas und die Kurve bricht aus. (Vgl. Abb. 4-6, Ausbruch der Kurve durch Ende der Kurve dargestellt)
Zwischen Katode und Anode zeigen sich in der Röhre Leuchterscheinungen, die bei genauem Hinsehen leichte Minima und Maxima erkennen lassen. (Vgl. Abb. 2, Die Minima und Maxima sind wegen der Qualität der Bildaufnahme nicht zu erkennen) Diese werden zahlreicher, je höher die Beschleunigungsspannung eingestellt ist. Die Farbe der Leuchterscheinung entspricht in etwa dem türkis von Quecksilberdampflampen. Beim Zünden des Gases zeigt sich eine anders geformte, stärkere Leuchterscheinung, der gleichen Farbe.
Auswertung
| Ordnung des Maximums | Spannungswert des Maximums in V | Daraus abgeleiteter Wert für ΔU in V |
|---|---|---|
| 3 | 20,7 | X |
| 4 | 25,4 | 4,7 |
| 5 | 30,3 | 4,9 |
| 6 | 35,2 | 4,9 |
| 7 | 40,1 | 4,9 |
| 8 | 44,8 | 4,7 |
| 9 | 49,9 | 5,1 |
| 10 | 54,9 | 5,0 |
| 11 | 60,0 | 5,1 |
| Mittwelwert und Standartabweichung | X | 4,91 ± 0,15 |
| Ordnung des Minimums | Spannungswert des Minimums in V | Daraus abgeleiteter Wert für ΔU in V |
|---|---|---|
| 2 | 18,1 | X |
| 3 | 23,1 | 5,0 |
| 4 | 27,7 | 4,6 |
| 5 | 32,5 | 4,8 |
| 6 | 37,5 | 5,0 |
| 7 | 42,2 | 4,7 |
| 8 | 47,2 | 5,0 |
| 9 | 52,2 | 5,0 |
| 10 | 57,2 | 5,0 |
| 11 | 62,2 | 5,0 |
| Mittwelwert und Standartabweichung | X | 4,89 ± 0,16 |
Daraus ergeben sich die Werte für die Anregungsenergie des dominanten Übergangs zu 4,91 ± 0,15 eV nach Messung der Spannungsdifferenzen zwischen den Maxima, 4,89 ± 0,16 eV für die Minima und 4,9 ± 0,2 eV, wenn man beide Werte verrechnet und die Fehler pytagoreisch addiert. Dabei wird allerdings angenommen, dass die Lösungen physikalisch gleichwertig sind. Das ist zwar nicht gegeben, kann für den schulischen Kontext aber eventuell vernachlässigt werden, wenn man genau ein Endergebnis haben möchte.
Ein großer Teil des Experiments lässt sich wie im Lehrbuch erklären. Die Elektronen werden beschleunigt, bis sie die notwendige Energie besitzen, um das Quecksilber auf sein zweites Energieniveau anzuregen. Nachdem sie das getan haben, verlieren sie ihre Energie und werden erneut beschleunigt, bis sie wieder die nötige Energie haben, um inelastisch mit dem Quecksilber zu stoßen und es damit anzuregen. Das gleiche Quecksilberatom kann mehrfach angeregt werden, weil der 63P1-Zustand instabil ist und sich das Atom unter Absonderung eines Photons wieder in den Grundzustand zurück begibt. Mithilfe des in Quelle 3 beschriebenen Experimentes, ließen sich diese Photonen auch nachweisen.
Für die Bestimmung der Energie muss der Abstand zwischen den Maxima statt der Abstand zwischen dem Nullpunkt und den Maxima verwendet werden, da es aufgrund der Kontaktspannungen zwischen Katode und Anode, sowie der unterschiedlichen Geschwindigkeiten der Elektronen beim Austritt aus der Katode einen Versatz U0 in x-Richtung gibt. Des Weiteren sind die ersten zwei Maxima und das erste Minimum nicht gut genug zu erkennen, um einen sinnvollen Wert entnehmen zu können.
Für eine Übersicht der Streuquerschnitte in Quecksilber siehe Quelle 4.
Aus dem großen Streuquerschnitt (der großen Wahrscheinlichkeit) der elastischen Stöße folgt aus der näherungsweise geradlinigen Beschleunigung der Elektronen eine nicht etwa geradlinige, sondern im Gegenteil näherungsweise isotrope Geschwindigkeits-/Bewegungsrichtung der Elektronen. Außerdem entsteht in Kombination mit der unterschiedlichen Anfangsgeschwindigkeit, mit der die Elektronen die Katode verlassen durch die vielen Stöße eine breite Energieverteilung, auch wenn die Elektronen pro Stoß nur einen kleinen Anteil ihrer Energie an die großen Atome abgeben (~2m/m0, mit 400000 mal größerer Atommasse m0). Deswegen ist statt einer strengen Sägezahnstruktur die vielfach gezeigte, typische Franck-Hertz-Kurve zu sehen, bei der die Minima nicht den Nullpunkt erreichen..
Der Versatz der Kurve in y-Richtung entsteht aus der inneren Spannung im Betriebsgerät. Zwischen „M“ und „Output“ wurde genau diese Spannung wiedergefunden. (Vgl. Abb. "Aufbau des F-H-V") Der Versatz in x-Richtung lässt sich aus dem Alter der Röhre erklären – sie könnte Luft gezogen haben und wegen des schwächeren Vakuums bräuchten die Elektronen eine größere Energie, um das Quecksilber das erste mal anzuregen. Außerdem gibt es Kontaktspannungen der unterschiedlichen Materialien zwischen Katode und Gitter. Auch die Anfangsgeschwindigkeit der Elektronen beim Austritt aus der Katode, beeinflusst diesen x-Versatz.
Aus den sichtbaren Leuchterscheinungen lässt sich schließen, dass neben den ersten drei Energieniveaus noch andere angeregt werden – nämlich die für die jeweiligen klassischen Quecksilberlinien 577 nm, 546 nm und 435 nm verantwortlichen oberen Energieniveaus. Das lässt auch darauf schließen, dass entgegen der Lehrbuchdarstellung die Energiedifferenz zwischen den Atomen größer sein kann als 1 eV. Das diese anderen angeregten Zustände nicht signifikant zur Kurve beitragen lässt sich aus der geringeren Wahrscheinlichkeit der Anregung erklären. Diese scheint zwar groß genug für sichtbare Emission zu sein, aber im Vergleich zur Wahrscheinlichkeit, das Atom mit 4,9 eV anzuregen verschwindend gering.
Literatur
- ↑ Vgl. Diehl, Bardo u.a.: Physik Oberstufe – Gesamtband, Cornelsen, Berlin, 2008, S. 337-339
- ↑ Vgl. auch Hildebrandt, Malte, sowie E. Robson und R.D. White: „Ein Grundstein der Atomphysik“ in M. Bartelmann u.a. (Hrsg.) Physik Journal, Heft 03/2014, Weinheim, 2014, S. 43-49
- ↑ Vgl. Kuhn, Wilfried (Hrsg.): Handbuch der experimentellen Physik – Sekundarbereich II, Band 8, Aulis, Köln, 1996, S. 239ff.
- ↑ Vgl. Quelle 2 S. 45