Fallkegel

Fallkegel
Überlagerung jedes 4ten Bildes einer Videoaufnahme (30 fps) eines fallenden Fallkegels
Kurzbeschreibung
Der Einfluss der Masse eines Fallkegels auf seine max. Endfallgeschwindigkeit wird mit Hilfe der Videoanalyse charakterisiert.
Kategorien
Mechanik, Freier Fall und Wurf
Einordnung in den Lehrplan
Geeignet für:	Sek I
Basiskonzept:	System, Wechselwirkung, Energie oder Materie
Sonstiges
Durchführungsform	Schülergruppenexperiment
Anzahl Experimente in dieser Unterkategorie	1
Anspruch des Aufbaus	mittel
Informationen
Name:	Stefanie Brück
Kontakt:	${\text{brueck-stefanie}}$@${\text{web.de}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Wiebke Musold

Fallkegel werden in vielen Lehrbüchern als geeignete Fallkörper zur Demonstration des Falls unter Einfluss des Luftwiderstandes beschrieben (Hilscher , 1998, S. 469 ff; Wilke , 2008, S. 53 f; Suleder, 2010, S. 62 ff.). Mit ihnen kann gezeigt werden, dass fallende Körper nach einer ungleichmäßig beschleunigten Bewegung in eine gleichförmige Bewegung mit konstanter Endgeschwindigkeit übergehen und dass diese Endgeschwindigkeit von der Geometrie und Masse des Fallkörpers abhängt. Ihr Vorteil besteht in ihrem geradlinigen und ausreichend langsamen Fallverhalten. Sie erreichen schon nach kurzer Fallstrecke ihre maximale Endfallgeschwindigkeit und die Parameter, welche die Endgeschwindigkeit beeinflussen, sind unabhängig voneinander einstellbar.

Im folgenden Experiment soll exemplarisch die Abhängigkeit der Endgeschwindigkeit von der Masse des Fallkegels untersucht werden. Die Fallkegel unterschiedlicher Masse werden dazu auf Video aufgenommen und das Videomaterial anschließend mit dem Programm Viana bearbeitet. Im Didaktischen Teil wird auf das Potenzial der Fallkegel zum schulischen Einüben der Variablenkontrollstrategie eingegangen.

Didaktischer Teil

Der Umgang mit Variablen beim Experimentieren ist eine der wichtigsten Arbeitsweisen in den Naturwissenschaften. Das Ziel eines Experiments ist in der Regel zu prüfen, ob ein Zusammenhang zwischen zwei Variablen besteht und gegebenenfalls diesen Zusammenhang zu charakterisieren (Schulz, Wirtz, & Starauschek , 2012, S. 16). In unserem Beispiel müssen die Schüler vor der Experimentplanung zunächst überlegen, welche potenziellen Einflussgrößen die Fallgeschwindigkeit des Kegels beeinflussen könnten. Die Vermutungen können aus entsprechenden Alltagsbeobachtungen (z.B. Vergleich eines fallenden Laubblattes und eines Tennisballes) oder theoretisch abgeleitet werden.

Abbildung 1: Variablen eines Fallkegels, welche die Endfallgeschwindigkeit beeinflussen

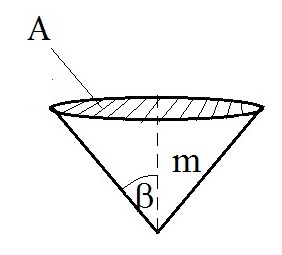
Die maximale Endgeschwindigkeit v eines fallenden Körpers hängt nach Formel (1) von seiner Masse m, seiner Querschnittsfläche A und seinem c_W-Wert ab (Singer , 2012). Dabei ist g die Erdbeschleunigung und $\rho$ die Dichte der Luft. Der c_W-Wert ist ein experimentell für jeden Flugkörper zu bestimmender Faktor, der wiederum von der Form des Körpers abhängt. Man kann sagen, je aerodynamischer die Form des Körpers ist, umso kleiner ist der c_W-Wert und umso schneller die Fallgeschwindigkeit. Übertragen auf den Fallkegel bedeutet dies, dass neben seiner Masse m und seiner Grundkreisfläche A auch der Öffnungswinkel $2\beta$ die Endfallgeschwindigkeit v beeinflusst. In Abbildung 1 ist ein Fallkegel mit den drei einflussnehmenden Größen dargestellt.

(1) $v={\sqrt {\frac {2mg}{c_{W}\rho A}}}$

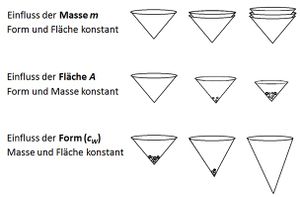
Da der Fall des Kegels von mehreren Einflussfaktoren abhängt, muss zur Identifikation und Charakterisierung von Variablenzusammenhängen die Variablenkontrollstrategie angewandt werden. Dazu wird die potenzielle Einflussgröße (z.B. die Masse des Fallkegels = Testvariable) aktiv variiert und der potenzielle Effekt (die Veränderung der Fallgeschwindigkeit = abhängige Variable) erfasst. Alle anderen potenziellen Einflussfaktoren (Form und Fläche des Kegels = Kontrollvariablen) werden konstant gehalten (vgl. Schulz, Wirtz, & Starauschek , 2012, S. 18). In Abbildung 2 ist gezeigt, wie die einflussnehmenden Variablen des Fallkegels unabhängig voneinander, bei gleichzeitiger Konstanz aller anderen Parameter, variiert werden können.

Abbildung 2: Schaubild zur kontrollierten Variation der Variablen, die die maximale Endfallgeschwindigkeit des Fallkegels beeinflussen

„Unterscheiden sich zwei Vergleichsbedingungen in einer Untersuchung nicht nur hinsichtlich der […] [Test-]Variablen, sondern auch noch hinsichtlich weiterer Merkmale, so spricht man von einer Variablenkonfundierung“ (Schulz, Wirtz, & Starauschek , 2012, S. 23). Die Einflüsse der verschiedenen veränderten Bedingungen vermischen sich dann untereinander, so dass die Wirkungen der Variablen nicht voneinander abzugrenzen sind. Die Kompetenz der Variablenkontrolle ist somit Voraussetzung für das selbstständige Planen von Experimenten (Hardy & Kempert , 2011, S. 30) . Diverse Studien zeigen, dass Schüler oft Schwierigkeiten mit dieser Strategie haben (Kuhn et al., 1995; Hammann et al., 2006; beide zitiert nach Rieß & Robin , 2012, S.133). So tendieren sie oft zu einer „konfundierenden Experimentierweise“ und halten bei der Untersuchung der Wirkung der Testvariablen die Kontrollvariablen nicht konstant (Klayman & Ha, 1989 zitiert nach Kirchner , 2013, S. 26).

Aufgrund dieser Feststellungen ist es empfehlenswert die Variablenkontrollstrategie und den Umgang mit Test-, Kontroll- und abhängigen Variablen mit den Schülern vermehrt im naturwissenschaftlichen Unterricht zu üben. Eine Möglichkeit dazu bietet die Untersuchung der einflussnehmenden Variablen eines fallenden Gegenstandes auf dessen Endgeschwindigkeit. Wie dies mit Hilfe des Fallkegels als Modellfallkörper umgesetzt werden kann, ist im Folgenden dargestellt.

Versuchsanleitung

Konstruktion der Fallkegel

Abbildung 3: Schnittmuster für einen Fallkegel

Abbildung 4: Zusammenhang zwischen den Parametern $\alpha$ und s der Kreisschablone und den Parametern U und $\beta$ des fertigen Fallkegels

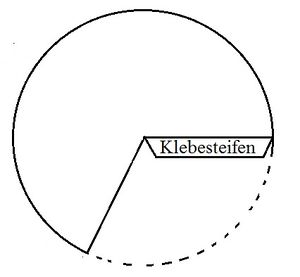
Für die Konstruktion der Fallkegel wird das in Abbildung 3 gezeigte Schnittmuster auf ein Blatt Papier übertragen, ausgeschnitten und der Klebestreifen an die gegenüberliegende Kante geklebt.

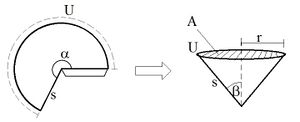
Der Öffnungswinkel $2\beta$ und der Grundkreisumfang U des Kegels sind letzlich die Variablen, über welche die Form und die Querschnittsfläche A des Fallkegels beeinflusst werden (s. Abbildung 4). Beide Größen, $\beta$ und U, lassen sich bei der Konstruktion des Kegels durch die Wahl des Kreisöffnungswinkels $\alpha$ und dem Kreisradius s einstellen. Die Größen hängen über folgende geometrischen Beziehungen zusammen:

(2) $\sin(\beta )={\frac {\alpha }{360^{\circ }}}$

(3) $U=2\pi r=2\pi s{\frac {\alpha }{360^{\circ }}}$

Aufbau

Für die Untersuchung der Massenabhängigkeit werden folgende Materialien benötigt:

• mindestens drei identische Fallkegel
• Videokamera mit Stativ (Belichtungszeit: 0,033 s)
• langes schwarzes Tuch
• Brett bekannter Länge (ideal: 1 m)
• ggf. Trittleiter

Für die Untersuchung der Massenabhängigkeit müssen alle Fallkegel den gleichen Öffnungswinkel $\beta$ und den gleichen Grundkreisumfang U aufweisen. Für die hier gezeigten Videoaufnahmen wurden für die Kreisschablonen ein Radius s von 3 cm und ein Kreisöffnungswinkel $\alpha$ von $270^{\circ }$ gewählt. Damit ergeben sich nach Formel (2) und (3) für die resultierenden Fallkegel ein Öffnungswinkel $2\beta$ von $97^{\circ }$ und ein Grundkreisumfang U von 28,3 cm. Die Querschnittsfläche A beträgt somit 63,6 cm². Ein einzelner Fallkegel wiegt 657 mg, so dass zwei (drei) zusammengesteckte Kegel 1,314 g (1,971 g) wiegen.

Damit die resultierenden Bildaufnahmen aufgrund der Bewegungsunschärfe nicht verschwimmen, ist eine kurze Belichtungszeit vorteilhaft. Die hier verwendete Kamera besitzt eine Bildrate von 30 fps, was einer Belichtungszeit von 33 ms entspricht. Das schwarze Tuch dient als kontrastgebender, homogener Hintergrund für die Videoaufnahmen und wird an einer Wand befestigt. Das Brett wird so positioniert, dass seine volle Länge in der Videoaufnahme zu sehen ist. Es dient der späteren Skalierung der Fallstrecke im Video.

Um die perspektivische Verzerrung im späteren Video zu vermeiden, sollte die Kamera senkrecht zur Bewegunsebene stehen und ein ausreichend großer Abstand gewählt werden. Die räumliche Kapazität begrenzt auch die zu analysierende Fallstrecke. Je größer der Abstand zwischen Kamera und Fallebene gewählt werden kann, umso länger ist die aufgenommene Fallstrecke. Es muss jedoch beachtet werden, dass in der nachfolgenden Videoanalyse die Unsicherheit beim Lokalisieren des Fallobjektes mit zunehmenden Abstand zwischen Kamera und Fallobjekt steigt.

Durchführung

Videoaufnahmen:

Unmittelbar vor der präparierten Wand wird ein Fallkegel von der Leiter aus mit der Spitze nach unten fallen gelassen. Der Fall wird mit der Kamera aufgenommen. Anschließend werden erst zwei und dann drei ineinander gesteckte Kegel fallen gelassen und gefilmt. Variation: Um das Videomaterial zu reduzieren können auch alle zusammengesetzten Kegel gleichzeitig auf einem Video aufgenommen werden. Für diese Variante müssen insgesamt sechs Kegel angefertigt werden. Außerdem muss durch eine geeignete Konstruktion gewährleistet werden, dass alle Kegel Ihren Fall gleichzeitig starten. Eine Möglichkeit, die für das später analysierte Video verwendet wurde, besteht darin, die Fallkegel zwischen dem waagerecht positionierten Skalierungsbrett und der Wand einzuklemmen. Durch schnelles Wegziehen können alle Kegel gleichzeitig und aus derselben Höhe fallen.

Abbildung 5: Erstellen von Videoschnappschüssen mit dem VLP Media Player

Erstellen eines Zeitrafferbildes:

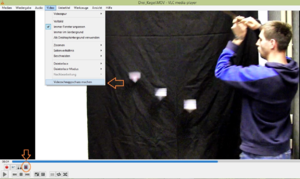
Um das Fallverhalten genauer zu analysieren wird aus dem Video ein Zeitrafferbild erstellt. Dazu kann das Bildmaterial mit dem VLC Media Player aufbereitet werden. Falls noch nicht geschehen wird unter dem Reiter "Ansicht" die "Erweiterte Steuerung" aktiviert. In der unteren Leiste erscheinen vier zusätzliche Items. Mit dem Item "Frame für Frame" (S. Abbildung 5) kann das Video Bild für Bild weitergeklickt werden. Immer nachdem das Video um 4 Bilder weiter geklickt wurde, wird unter dem Reiter "Video" mit dem entsprechenden Befehl ein Videoschnappschuss erstellt. Unter dem Reiter "Werzeuge" befinden sich die "Einstellungen". Unter den "Video-Einstellungen" kann der Zielordner für die erstellten Schnappschüsse ausgewählt werden. Die Bilder werden anschließend in einem Bildbearbeitungsprogramm, z.B. Adobe Photoshop CS2, geladen, jeweils unterhalb der jeweiligen Fallkegelpositionen beschnitten und übereinander in ein Bild gelegt.

Abbildung 6: Videoanalyse mit Viana. Net 5.0

Videoanalyse mit Viana:

Das Videomaterial wird mit dem Programm Viana. Net 5.0 geladen und bearbeitet (s. Abbildung 6). Zunächst wird durch Verschieben der Marker in der unteren Leiste der relevante Bereich des Videos ausgewählt (1). Anschließend wird das Video anhand des gefilmten Bretts bekannter Länge eingemessen (2) und der Koordinatenursprung (0,0) und die Koordinatenachsen festgelegt (3). Funktionalerweise wird der Koordinatenursprung auf die Position des ruhenden Fallkegels gelegt und die y-Richtung des Koordinatenkreuzes nach unten in die Fallrichtung positioniert. Nach diesen Voreinstellungen kann die Objektverfolgung beginnen. Da es auch schon bei einer Bildrate von 30 fps mit fortschreitender Fallgeschwindigkeit zu Bewegungsunschärfen kommt, ist die automatische Objektverfolgung ungeeignet (Analyse: "Automatischen Modus starten"). Mit dem Programm kann die Positionen der Fallkegel während des Fallens auch manuell lokalisiert werden. Pro Analyse können dabei, je nach Einstellung, bis zu drei Objekte gleichzeitig verfolgt werden (4). Anschließend wird unter Start: "Manuellen Modus starten" die Objektverfolgung begonnen (5). Da der Auswahlkreis deutlich kleiner als der abgebildete Fallkegel ist, sollte der Kegel immer an derselben Stelle getroffen werden. Als einfachste Lösung hat sich die Positionierung der Kegelspitze erwiesen, da diese immer gut zu erkennen und eindeutig festzulegen ist. Außerdem wird dadurch gewährleistet, dass trotz der Bewegungsunschärfe zwischen den ausgewählten Fallstrecken immer die gleiche Zeitspanne besteht. Nach der Objektverfolgung liefert das Programm automatisch eine Datentabelle mit der Fallzeit, der zugehörigen zurückgelegten Strecke, der Geschwindigkeit und der Beschleunigung.

Ergebnisse

Im folgendem Video ist der Fall der drei unterschiedlich schweren Fallkegel zu sehen. Die Masse nimmt von links nach rechts um jeweils eine Einheit zu.

Schon im Video ist zu erkennen, dass die Fallgeschwindigkeit mit zunehmender Masse steigt. Der Prozess ist jedoch sehr schnell, so dass durch die Beobachtung mit dem blossen Auge keine weiteren Aussagen getroffen werden können. Um das Fallverhalten genauer zu untersuchen, wurde ein Zeitrafferbild erstellt und eine Videoanalyse durchgeführt. In der folgenden Auswertung sind die Ergebnisse gezeigt.

Auswertung

Zeitrafferbild:

Abbildung 7: Zeitrafferbild (Überlagerung jedes 4. Bildes der Videoaufnahme)

In Abbildung 7 ist das erstellte Zeitrafferbild zu sehen. Da es sich um eine Überlagerung jedes vierten Bildes im Video handelt, zeigt es die aufeinanderfolgenden Positionen der drei Fallkegel im 0,14 Sekunden-Takt. Was zuvor im Video ansatzweise zu erkennen war, wird im Bild viel deutlicher:

1.) Für alle drei Kegel gilt: Die in einer Zeiteinheit zurückgelegte Fallstrecke nimmt während des Fallens zunächst zu.

2.) Nach einer bestimmten Zeit bleibt die in einer Zeiteinheit zurückgelegte Fallstrecke konstant. Diese Strecke ist umso größer, je schwerer der Fallkegel.

3.) Die Konstanz erreicht der Kegel 1 schon nach vier Zeiteinheiten, der Kegel 2 nach sechs und für den schwersten Kegel 3 nehmen die aufeinanderfolgenden Fallstrecken bis zum Ende zu.

Videobearbeitung mit Viana:

Die in Viana nach der Objektverfolgung automatisch generierten Daten wurden in das Programm Origin 8.5 exportiert um ein Weg-Zeit- und ein Geschwindigkeits-Zeit-Diagramm anzufertigen. Um die Fehler der Fallstrecke s und der Momentangeschwindigkeit v in den Auftragungen miteinzubeziehen muss die von Viana automatisch erfolgte Datengenerierung nachvollzogen werden. Die Lokalisierung der Kegelposition p_n in Viana erfolgte mit einer Unsicherheit u(p_n), die auf 3 Pixel abgeschätzt wurde, was im Video einer Länge von 0,5 cm entspricht. Die zurückgelegte Fallstrecke s (4) und der zugehörige Fehler u_s (5) berechnen sich aus der Urspungsposition p₀ und der jeweilig aktuellen Position des Kegels p_n wie folgt:

(4) $s=p_{n}-p_{0}$
(5) $u_{s}={\sqrt {u(p_{n})^{2}-u(p_{0})^{2}}}$

Für die zurückgelegte Fallstecke s ergibt sich damit eine Unsicherheit u_s von 0,7 cm.

Die jeweilige Momentangeschwindigkeit v wurde von Viana aus jeweils zwei aufeinanderfolgenden Datenpunkten (t_n, s_n) und (t_n+1, s_n+1) berechnet (6). Der zugehöriger Fehler u_v ergibt sich dann nach Gleichung (7):

(6) $v={\frac {s_{n+1}-s_{n}}{t_{n+1}-t_{n}}}$

(7) $u_{v}={\sqrt {({\frac {u(s_{n})}{t_{n+1}-t_{n}}})^{2}+({\frac {u(s_{n+1})}{t_{n+1}-t_{n}}})^{2}}}$

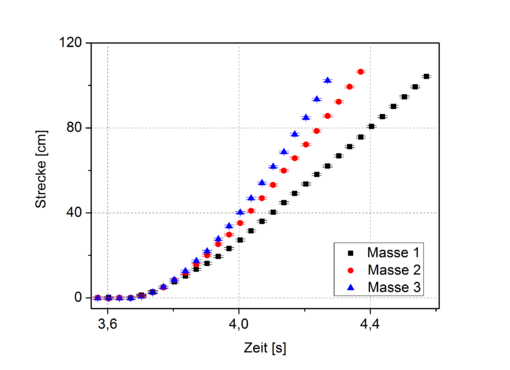
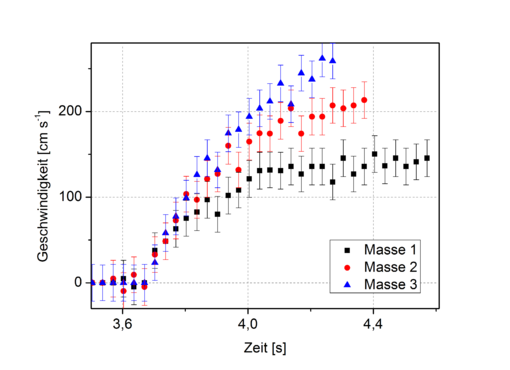
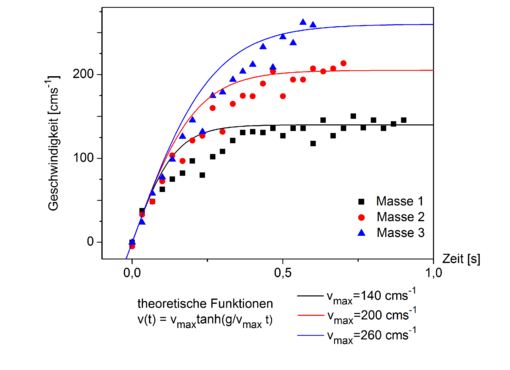
In Abbildung 8 (9) ist die Auftragung der zurückgelegten Strecken (der Geschwindigkeiten) gegen die Fallzeit für die drei Fallkegel unterschiedlicher Masse abgebildet. Die Weg-Zeit-Kurven erinnern zunächst an Fallparabeln und gehen dann jeweils unterschiedlich schnell in eine Gerade über. In den Geschwindigkeits-Zeit-Auftragungen steigen die Geschwindkeiten zunächst an und nehmen dann unterschiedlich schnell unterschiedlich große Grenzwere an. Die Auftragungen verdeutlichen:

1.) Alle drei Kegel gehen nach einer anfänglich beschleunigten Bewegung in eine gleichförmige über und fallen mit konstanter Geschwindigkeit weiter.

2.) Die Endfallgeschwindikeit nimmt mit steigender Masse des Kegels zu. So erreicht Kegel 1 nur eine Fallgeschwindigkeit von 140 cm s^-1, Kegel 2 erreicht schon 200 cm s^-1 und für Kegel 3 reicht die aufgenommene Fallstrecke nicht aus, um seine maximale Geschwindigkeit zu erreichen. Schätzungsweise liegt diese bei ungefähr 260 cm s^-1.

3.) Die Endfallgeschwindigkeit wird umso früher erreicht, je geringer die Masse des Kegels ist. Der schwerste Kegel beschleunigt am längsten.

Eine schön formulierte Erklärung für das generalle Fallverhalten findet man in Suleder, 2010:

"Während der freie Fall eine Bewegung ohne Reibungsflüsse beschreibt, ist nun eine geschwindigkeitsabhängige Luftreibungskraft zu berücksichtigen[, die entgegen der Bewegungsrichtung wirkt].[...] Im Augenblick des Loslassens wirkt noch keine Luftreibungskraft auf den Fallkegel, sondern nur die Gewichtskraft. Die Bewegung ist also gleichförmig beschleunigt mit der Fallbeschleunigung g. Im weiteren Verlauf nimmt die Geschwindigkeit so lange zu, bis die Gewichtskraft und die geschwindigkeitsabhängige Reibungskraft einen Geleichgewichtszustand erreichen. Nach einer gewissen Flugzeit bewegt sich der Fallkegel deshalb mit konstanter Geschwindigkeit. (S. 62)"

Abbildung 8: Weg-Zeit-Diagramm für die drei Fallkegel unterschiedlicher Masse.

Abbildung 9: Geschwindigkeit-Zeit-Diagramm für die drei Fallkegel unterschiedlicher Masse.

Um die Endfallgeschwindigkeit für schwerere Kegel zu ermitteln, reicht die mit der Kamera aufgenommene Fallstrecke nicht aus, da sie über eine längere Strecke beschleunigen. Die Strecke reicht gerade so aus, um die Endgeschwindigkeit von Kegel 3 abzuschätzen. Eine Möglichkeit die zu analysierende Fallstrecke zu vergrößern, ist die Kamera vertikal auszurichten oder die Entfernung der Kamera zu den Fallkegel zu erhöhen. In einem Schulraum ist in der Regel eine Fallhöhe bis zu 2 m realisierbar (Für Videoaufnahmen im Freien eignen sich die Fallkegel nicht, da schon leichte Windstöße den geradlinigen Fall beeinflussen und stören). Möchte man vor den Schülern den Fall unter Luftwiderstand demonstrieren, muss die Geometrie und die Masse der Fallkegel so gewählt werden, dass sie innerhalb der zur Verfügung stehenden Fallstrecke ihre Beschleunigung abschließen und ihre maximale Geschwindigkeit erreichen.

Berechnung des c_W-Wertes:

Abbildung 1: c_W-Werte von Keil (schraffiert) und Kegel nach Arie und Rouse (1965), Kramer (1964), Hoerner (1965) und Tanner (1967). Graphik in Rodi & Mulas (2005)

Mit den erfassten Daten kann der c_W-Wert für den verwendeten Fallkegel ermittelt werden. Da der c_W-Wert nur von der Form des Fallkörpers abhängt und alle denselben Öffnungswinkel von 97 Grad aufweisen, sollte der Wert für alle drei unterschiedlich schweren Fallkegel gleich sein. Für die Berechnung wurde Formel (1) umgestellt:

(8) $c_{W}={\frac {2mg}{v^{2}\rho A}}$

Für die Luftdichte $\rho$ wurde ein Wert von 1,21 kg m^-3 und für die Erbeschleunigung g ein Wert von 9,81 m s^-2 angenommen (Halliday et al. , 2007, Erdbeschleunigung auf S. 30 und Luftdichte auf S. 311). Durch Einsetzten der Querschnittsfläche A von 63,6 cm² und den ermittelten Endgeschwindigkeiten für die jeweiligen Massen ergeben sich folgende Werte:

Masse [g]	cW-Wert
m1: 0.657	0.85
m2:1.314	0.84
m3:1.971	0.74

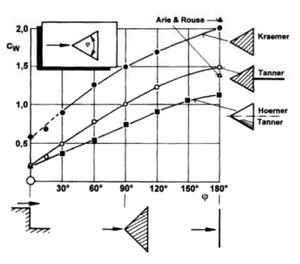
Die drei Messungen ergeben wie erwartet drei nah beieinander liegende Werte. Auf der Internetseite des Lehrstuhls für Strömungsmechanik und Strömunstechnik der Universität Magdeburg findet man für einen Fallkegel mit einem Öffnungswinkel von 30 Grad einen c_W-Wert von 0.35 und für einen Fallkegel mit einem Öffnungswinkel von 60 Grad einen Wert von 0.52. Unser Fallkegel mit einem Öffnungswinkel von 97 Grad gliedert sich damit in die Reihe ein. Die ermittelten Werte liegen auch im Bereich der experimentell ermittelten Werte von Hoerner (1965) und Tanner (1967) (siehe Abbildung 10).

Vergleich mit theoretischen Funktionsgraphen:

Die Geschwindigkeits-Zeit-Funktion (Herleitung aus der Bewegungsgleichung in Singer , 2010) eines fallenden Körpers, auf den seine Gewichtskraft und die Luftwiderstandskraft wirken, lautet:

(9) $v(t)=v_{max}tanh({\frac {g}{v_{max}}}t)$

Die Integration der Geschwindigkeits-Funktion liefert uns die Weg-Zeit-Funktion (Vgl. Lechner , 1998):

(10) $s(t)={\frac {v_{max}^{2}}{g}}ln(cosh({\frac {g}{v_{max}}}t))$

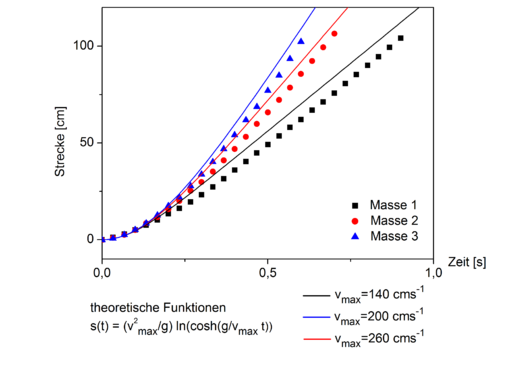
In Abbildung 11 und 12 wurden zusätzlich zu den experimentiell ermittelten Weg- und Fallgeschwindigkeits-Werten die theoretischen Funktionen nach Formel (9) und (10) aufgetragen, wobei für $v_{max}$ die experimentiell ermittelten Endgeschwindigkeiten angenommen wurden. In Abbildung 11 ist zu erkennen, dass die experimentiellen Weg-Werte entsprechend der theoretischen Funktion ansteigen, für höhere Zeiten jedoch generell unterhalb der theoretischen Werte liegen. Im Geschwindigkeits-Zeit-Diagramm ähneln die experimentiellen Werte dem Verlauf der theoretischen Funktionen, sind jedoch für mittlere Zeiten geringer als die theoretischen Werte, so dass sie eine weniger scharfe Kurve beschreiben. Generell werden die experimentiellen Daten gut durch die theoretischen Funktionen beschreiben. Messtechnisch bedingte Ungenauigkeiten, wie die Bildverschwimmung bei der Messung höherer Geschwindigkeiten und die perspektivische Verzerrung bei größeren Fallhöhen führen jedoch zu kleinen Abweichungen. Geringe Druckunterschiede und Störungen wie unerwünschte Luftzüge werden in der Theorie nicht berücksichtigt, so dass es sich trotz der Berücksichtigung des Luftwiderstandes immernoch um eine Idealisierung handelt.

Abbildung 11: Vergleichende Auftragung der experimentiell ermittelten Weg-Werte und der theoretischen Funktionsgraphen nach Formel (10).

Abbildung 12: Vergleichende Auftragung der experimentiell ermittelten Geschwindigkeits-Werte und der theoretischen Funktionsgraphen nach Formel (9).

Sicherheitshinweise

Um die Fallhöhe zu vergrößern sollten nur dafür vorgesehene und instante Trittleitern verwendet werden!