Experimentierreihe: Elektromagnetische Schwingungen (Oberstufe)

Experimentierreihe: Elektromagnetische Schwingungen (Oberstufe)
Kurzbeschreibung
Diese Unterrichtsreihe enthält Anleitungen zu Versuchen aus dem Themengebiet der elektromagnetischen Schwingungen
Kategorien
Elektrizitätslehre, Induktion,Unterrichtsmaterialien
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	System
Sonstiges
Durchführungsform	Schüler*innen-Experiment, Gruppenexperiment
Anzahl Experimente in dieser Unterkategorie	15-16
Anspruch des Aufbaus	leicht-mittel
Informationen
Name:	Christian Strube, Lilly Pyras
Kontakt:	${\text{lilly.pyras}}$@${\text{hu-berlin.de}}$
Uni:	Humboldt-Universität zu Berlin

Diese Experimentierreihe ist für den Unterricht der Sek. II geeignet. Zu Beginn werden Gleich- und Wechselspannung behandelt und verschiedene Bauteile wie Ohm'scher Widerstand, Induktivitäten (Spule) und kapazitive Elemente (Kondensator) in passenden Experimenten untersucht. Der Verlauf von Spannung und Stromstärke wird verdeutlicht. Anschließend werden Schwingung, Resonanz betrachtet. Zum Schluss gibt es Versuche zu speziellen Schalkreisen, z.B. Tief- und Hochpassfilter und R-C-Filter.

Alle Versuche sind als Word Datei angehangen, sodass sie als Arbeitsblatt ausgeteilt werden können.

Übersicht aller verwendeten Geräte

• Labornetzgerät
• Kondensator (C = 1 µF, 4,7 µF, 100 µF, 470 µF, 2200 µF)
• Spule (n = 500, 1000)
• 2 Spulen mit Eisenkern n = 1000 (in Reihe auf einem geschlossenen Eisenkern) und n = 500
• mehrere Widerstand R = 10 Ω, 100 Ω, 1 kΩ
• Multimeter zur Frequenzmessung (z.B. Uni-T UT61B 40€)
• 2 Multimeter U~ und I~
• 2 Zeigermessinstrumente (z. B. Conatex Demomultimeter ca. 520€)
• 3 Glühlampe
• 2 LED
• Magnetnadel / Kompass
• Funktionsgenerator für Schüler*innen (z. B. LD Funktionsgenerator S 12, ca. 440€; Winlab Funktionsgenerator SE ca. 230€)
• Taschen-Osziloskop für Schüler*innen (z. B. Quimat 2,4" TFT Digital Oszilloskop, 30€)

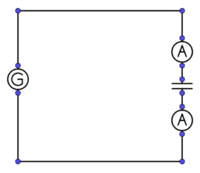
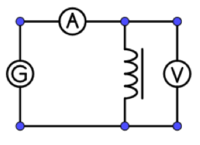
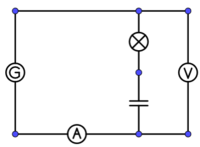
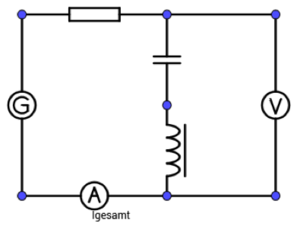
1. Kondensator und Spule im Wechselstromkreis

Geräte

• Labornetzgerät
• Kondensator C = 470 µF
• 2 Zeigermessinstrumente
• Spule (n = 500) mit Eisenkern
• Magnetnadel / Kompass
• Multimeter zur Frequenzmessung

Versuchsbeschreibung

Das Verhalten von Kondensator und Spule im Wechselstromkreis soll qualitativ untersucht werden.

Versuch 1:

Versuch 1

Stellen Sie bei beiden Zeigermessinstrumenten den Zeiger in Mittelstellung.
Stellen Sie für den Messbereich der Stromstärke I = 1 mA (A = ) ein.
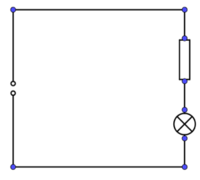
Bauen Sie die Schaltung entsprechend dem nebenstehenden Schaltplan auf.
Stellen Sie am Funktionsgenerator folgende Werte ein:
U = 1 V, f = 0,2 Hz

Notieren Sie anschließend Ihre Beobachtungen und Ergebnisse.

Versuch 2:

Versuch 2

Schließen Sie den Funktionsgenerator an die Spule mit dem Eisenkern an. Stellen Sie vor die Spule die Magnetnadel/den Kompass.
Stellen Sie am Funktionsgenerator folgende Werte ein:
U = 3 V (maximal), f = 0,2 Hz

Notieren Sie anschließend Ihre Beobachtungen und Ergebnisse.

Versuch 3:

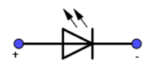
Versuch 3

Eine LED lässt den elektrischen Strom nur in eine Richtung passieren (von + nach -) und leuchtet dabei auf (sie emittiert dabei Licht → Licht emittierende Diode).

Bauen Sie die nebenstehende Schaltung auf. Stellen Sie für die Frequenz f = 0,2 Hz ein.
Regeln Sie die Spannung langsam nach oben, bis die LED’s leuchten.
Stellen Sie die Magnetnadel (Kompass) vor die Spule.

Beobachten Sie die Anordnung für verschiedene Frequenzen.

Notieren Sie anschließend Ihre Beobachtungen und Ergebnisse.

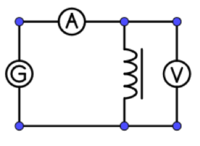
2. Widerstand, Kondensator und Spule

Geräte

• Labornetzgerät
• Glühlampe
• Widerstand R = 10 Ω
• Kondensator C = 100 µF
• Spule n = 1000
• Eisenkern

Versuchsbeschreibung

Die Eigenschaften von Widerstand R, Kondensator C und Spule L im sollen im Gleichstromkreis und im Wechselstromkreis untersucht und verglichen werden. Vergleichen Sie die Helligkeit der Lampe bei den verschiedenen Schaltungen.

Versuch:

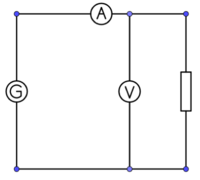
Bauen Sie die Schaltung entsprechend dem Schaltplan auf.
a) Legen Sie eine Gleichspannung an und bringen Sie die Lampe zum Leuchten. U = _____V
b) Legen Sie jetzt eine Wechselspannung an und versuchen Sie, die gleiche Helligkeit der Lampe einzustellen. Die Wechselspannung hat jetzt effektiv die gleiche Wirkung wie die vorherige Gleichspannung (U_eff = _____V). → Verwenden Sie nachfolgend diese Werte!
c) Ersetzen Sie jetzt den Widerstand durch den Kondensator. (Polung beachten!) Beobachten Sie die Helligkeit der Lampe bei Gleich- und Wechselspannung.
d) Ersetzen Sie jetzt den Kondensator durch die Spule (ohne Eisenkern) und beobachten Sie die Helligkeit der Lampe bei Gleich- und Wechselspannung.
e) Schieben Sie jetzt den Eisenkern in die Spule und beobachten Sie die Helligkeit der Lampe bei Gleich- und Wechselspannung.

Beobachtung

Helligkeit der Lampe

	Gleichspannung	Wechselspannung
	_____________V	_____________V
Widerstand
Kondensator
Spule
Spule mit Eisenkern

3. Zeitlicher Verlauf von Spannung und Stromstärke (1)

Geräte

• Labornetzgerät
• Funktionsgenerator
• 2 Zeigermessinstrumente
• Widerstand R = 100 Ω
• Kondensator C = 2200 µF
• 2 Spulen n = 1000 (in Reihe auf einem geschlossenen Eisenkern)

Versuchsbeschreibung

Der zeitliche Verlauf von Spannung und Stromstärke soll mit Hilfe der beiden Zeigermessinstrumente beobachtet werden.

Versuch:

Stellen Sie bei beiden Messinstrumenten den Zeiger in Mittelstellung.
Stellen Sie folgende Messbereiche ein:
U (V=) = 3 V , I(A=) = 100 mA

Bauen Sie die Schaltung wie im Schaltplan dargestellt auf.

Stellen Sie am Funktionsgenerator die Werte U = 3 V und f = 0,2 Hz ein.

a) Beobachten Sie für den Widerstand R den zeitlichen Verlauf von Spannung und Stromstärke an den beiden Messgeräten.
b) Ersetzen Sie den Widerstand R durch den Kondensator C. Beobachten Sie für die gleiche Einstellung am Funktionsgenerator den zeitlichen Verlauf von Spannung und Stromstärke.
c) Ersetzen Sie den Kondensator C durch die Spule L (Spulenpaar) und beobachten Sie den zeitlichen Verlauf von Spannung und Stromstärke.

4. Zeitlicher Verlauf von Spannung und Stromstärke (2)

Geräte

• Labornetzgerät
• 2 Widerstände R = 100 Ω
• Kondensator C = 2200 µF
• 2 Spulen n = 1000 (in Reihe auf einem geschlossenen Eisenkern)
• 2 LED

Versuchsbeschreibung

Der zeitliche Verlauf von Spannung U und Stromstärke I sollen untersucht werden.

Versuch:

Bauen Sie die Schaltung entsprechend der nebenstehenden Abbildung auf.

Stellen Sie am Funktionsgenerator folgende Werte ein: U = 3 V, f = 0,2 - 1 Hz

a) Beobachten Sie beide LED. Das Aufleuchten der LED ist ein Maß für die Spannung U am Widerstand und zeigt gleichzeitig den elektrischen Strom I an.
b) Ersetzen Sie jetzt den oberen Widerstand R durch den Kondensator C. Das Aufleuchten der oberen LED zeigt jetzt die Spannung am Kondensator U_C an, das Aufleuchten der unteren LED die Spannung am Widerstand UR. c) Ersetzen Sie jetzt den Kondensator C durch die Spule L (Spulenpaar). Das Aufleuchten der oberen LED zeigt jetzt die Spannung an der Spule U_L an, das Aufleuchten der unteren LED die Spannung am Widerstand U_R.

Notieren Sie anschließend Ihre Beobachtungen und Ergebnisse.

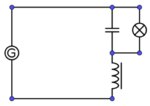
5. Wechselstromwiderstand X_C eines Kondensators

Geräte

• Labornetzgerät
• Kondensator 1 µF
• 2 Multimeter U~ und I~
• Multimeter zur Frequenzmessung

Versuchsbeschreibung

Die Abhängigkeit des Wechselstromwiderstandes eines Kondensators XC von der Frequenz soll untersucht werden. Die ohmschen Widerstände R (z.B. der Zuleitungen) werden vernachlässigt.

Versuch:

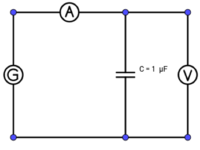
Bauen Sie die Schaltung entsprechend dem nebenstehen Schaltplan auf.

Die zu erwartenden Messbereiche (Wechselspannung und Wechselstrom AC) liegen für die Spannung im Bereich um U = 3 V ~ und I = 10 mA~.

Versuch 1:

Stellen Sie am Funktionsgenerator eine Spannung von 3 V ein und messen Sie Spannung und Stromstärke für Frequenzen zwischen f = 50 Hz und f = 500 Hz. Die nachstehende Tabelle eignet sich zur Aufzeichnung der Messdaten.

Versuch 2:

Schalten Sie einen 2. Kondensator mit C₂ = 1 µF parallel und messen Sie Spannung und Stromstärke für Frequenzen zwischen f = 50 Hz und f = 500 Hz für eine Kapazität von C = 2 µF (C = C₁ + C₂). Auch diese Werte können in eine zweite Tabelle der nachstehenden Form eingetragen werden.

f in Hz	50	100	150	200	250	300	350	400	450	500
U in V
I in mA
XC=U/I in Ω

Aufgabe 1:

Erstellen Sie auf der Rückseite ein f-X_CC-Diagramm, das beide Messreihen enthält.

Aufgabe 2:

Analysieren Sie die Tabelle mit den Messwerten auf der Rückseite und formulieren Sie einen mathematischen Zusammenhang zwischen den Größen X_C, f und C.

Messwerte für U_eff = 10 V für C₁ = 50 nF, C₂ = 100 nF und C₃ = 150 nF

Kapazität C	50 nF	50 nF	100 nF	100 nF	200 nF	200 nF
f/Hz	Ieff in mA	Ueff/Ieff in kΩ	Ieff in mA	Ueff/Ieff in kΩ	Ieff in mA	Ueff/Ieff in kΩ
50	0,159	62,893	0,318	31,446	0,636	15,723
100	0,318	31,446	0,636	15,723	1,273	7,855
200	0,636	15,723	1,273	7,855	2,546	3,927
400	1,273	7,855	2,546	3,927	5,092	1,963
800	2,546	3,927	5,092	1,963	10,18	0,982
1600	5,092	1,963	10,10	0,982	20,37	0,491
3200	10,18	0,982	20,37	0,491	40,73	0,245
6400	20,37	0,491	40,73	0,245	81,48	0,123

Hinweise:

Mögliche Ergebnisse wären:

f in Hz	50	100	150	200	250	300	350	400	450	500
I in mA	0,9424778	1,88495559	2,82743339	3,76991118	4,71238898	5,65486678	6,59734457	7,53982237	8,48230016	9,42477796
XC=U/I in Ω	3183,09886	1591,54943	1061,03295	795,774715	636,619772	530,516477	454,728409	397,887358	353,677651	318,309886

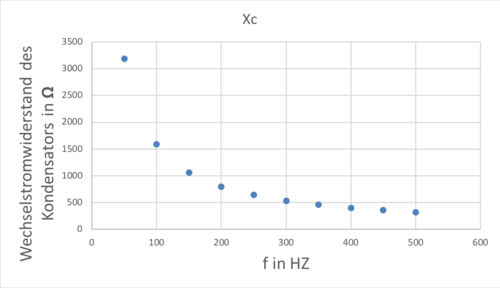
Abb. Wechselstromwiderstand eines Kondensators in Abhängigkeit der Frequenz.

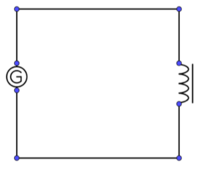
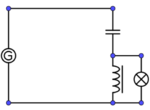
6. Wechselstromwiderstand X_L einer Spule (1)

Geräte

• Labornetzgerät
• Spule n = 1000
• 2 Multimeter U~ und I~
• Multimeter zur Frequenzmessung

Versuchsbeschreibung

Die Abhängigkeit des Wechselstromwiderstandes einer Spule X_L von der Frequenz soll untersucht werden. → Der ohmsche Widerstand R der Spule wird zunächst vernachlässigt.

Versuch 1:

Bauen Sie die Schaltung entsprechend dem nebenstehen Schaltplan auf.
Die Spule (n = 1000) hat mit Eisenkern (I-Kern) eine Induktivität von L = 109 mH.

Die zu erwartenden Messbereiche (Wechselspannung und Wechselstrom AC) liegen für die Spannung im Bereich um U = 3 V ~ und I = 100 mA~.

Stellen Sie am Funktionsgenerator eine Spannung von 3 V ein und Messen Sie Spannung und Stromstärke für Frequenzen zwischen f = 50 Hz und f = 500 Hz.

Versuch 2:

Führen Sie die gleiche Messreihe für eine Spule mit n = 1000 ohne Eisenkern durch (L = 18 mH) durch.

f in Hz	50	100	150	200	250	300	350	400	450	500
U in V
I in mA
XL=U/I in Ω

Aufgabe 1:

Erstellen Sie auf der Rückseite ein f-XL-Diagramm, das beide Messreihen enthält.

Aufgabe 2:

Analysieren Sie die Tabelle mit den Messwerten auf der Rückseite und formulieren Sie einen mathematischen Zusammenhang zwischen den Größen X_L, f und L.

Für U_eff = 10 V wurde der sich bei den verschiedenen Frequenzen f einstellende Strom I_eff für drei verschiedene Spulen (L₁ = 50 mH, L₂ = 100 mH, L₃ = 200 mH) gemessen.

Kapazität C	50 mH	50 mH	100 mH	100 mH	200 mH	200 mH
f/Hz	Ieff in mA	Ueff/Ieff in Ω	Ieff in mA	Ueff/Ieff in Ω	Ieff in mA	Ueff/Ieff in Ω
50	628	15,9	314	31,8	157	63,6
100	314	31,8	157	63,6	78,5	127,3
200	157	63,6	78,5	127,3	39,3	254,5
400	78,5	127,3	39,3	254,4	19,64	509
800	39,3	254,4	19,64	509	9,82	1018
1600	19,64	509	9,82	1018	4,91	2036
3200	9,82	1018	4,91	2036	2,455	4073
6400	4,91	2036	2,455	4073	1,228	8143

Hinweise:

Mögliche Ergebnisse wären:

f in Hz	50	100	150	200	250	300	350	400	450	500
I in mA	98,4463566	49,2231783	32,8154522	24,6115891	19,6892713	16,4077261	14,0637652	12,3057946	10,9384841	9,84463566
XL=U/I in Ω	30,4734487	60,9468975	91,4203462	121,893795	152,367244	182,840692	213,314141	243,78759	274,261039	304,734487

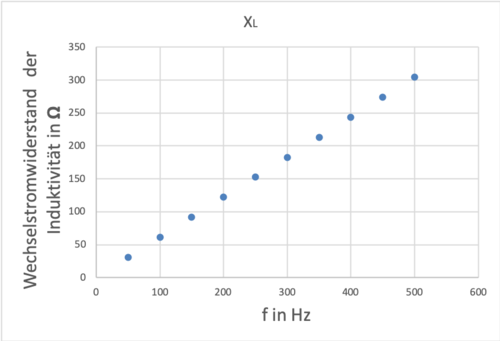
Abb. Wechselstromwiderstand der Spule in Abhängigkeit der Frequenz.

7. Wechselstromwiderstand X_L einer Spule (2)

Geräte

• Labornetzgerät
• Spule n = 1000
• 2 Multimeter U~ und I~
• Multimeter zur Frequenzmessung

Versuchsbeschreibung

Die Abhängigkeit des Wechselstromwiderstandes einer Spule X_L von der Frequenz soll untersucht werden. → Der ohmsche Widerstand R der Spule wird gemessen und bei der Auswertung berücksichtigt

Versuch:

Bauen Sie die Schaltung entsprechend dem nebenstehen Schaltplan auf. Die Spule (n = 1000) hat mit Eisenkern eine Induktivität von L = 109 mH.

Der ohmsche Widerstand der Spule R ist von der Frequenz unabhängig und wird vor der Messreihe mit dem Multimeter gemessen.

Der Wechselstromgesamtwiderstand Z ist dann: $Z={\sqrt {R^{2}+X_{L}^{2}}}$.
Die Größe Z kann aus den Messwerten berechnet werden: $Z={\frac {U_{e}ff}{I_{e}ff}}$.
Bei bekanntem ohmschen Widerstand R kann X_L aus den Messwerten bzw. Z berechnet werden.

Die zu erwartenden Messbereiche (Wechselspannung und Wechselstrom AC) liegen für die Spannung im Bereich um U = 3 V ~ und I = 100 mA~.

Stellen Sie am Funktionsgenerator eine Spannung von 3 V ein und Messen Sie Spannung und Stromstärke für Frequenzen zwischen f = 50 Hz und f = 500 Hz.

f in Hz	50	100	150	200	250	300	350	400	450	500
U in V
I in mA
Z =U/I in Ω
R in Ω
XL in Ω

$Z={\sqrt {R^{2}+X_{L}^{2}}}$ → $X_{L}=...$

8. Spule und Kondensator im Wechselstromkreis (1)

Geräte

• Labornetzgerät
• Kondensator C = 470 µF
• Kondensator C = 1 µF
• Spule n = 1000 mit Eisenkern
• Widerstand R = 100 Ω
• Glühlampe
• Multimeter als Messgerät für die Frequenz

Versuchsbeschreibung

Versuch 1

Die Eigenschaften von Widerstand R, Kondensator C und Spule L im Wechselstromkreis sollen qualitativ untersucht werden.

Versuch 1:

Schließen Sie nur eine Glühlampe an den Ausgang des Funktionsgenerators an.
a) Stellen Sie eine Frequenz von f = 10 Hz ein.
b) Stellen Sie eine Frequenz von f = 1 Hz ein.
c) Ermitteln Sie die Frequenz, bei der Sie das Blinken der Lampe nicht mehr wahrnehmen können.
Mit einem Handy (mit Slow-Motion-Funktion) können Sie nachweisen, dass die Glühlampe immer noch blinkt, obwohl es mit dem bloßen Auge nicht mehr wahrnehmbar ist.

Versuch 2:

Versuch 2

Bauen Sie einen Stromkreis aus einem ohmschen Widerstand R und einer Glühlampe auf.
Vergleichen Sie die Helligkeit der Lampe bei verschiedenen Frequenzen.

1 Hz	10 Hz	50 Hz	100 Hz	1000 Hz	10000 Hz
_______	_______	_______	_______	_______	_______

Fassen Sie Ihre Beobachtungen in einem Satz zusammen.

Versuch 3:

Ersetzen Sie den Widerstand R durch einen Kondensator C.
Vergleichen Sie die Helligkeit der Lampe bei verschiedenen Frequenzen.
Wiederholen Sie den Versuch mit einem Kondensator mit einer anderen Kapazität C.

Frequenz	1 Hz	10 Hz	50 Hz	100 Hz	1000 Hz	10000 Hz
Kondensator C1	_______	_______	_______	_______	_______	_______
Kondensator C2	_______	_______	_______	_______	_______	_______

Ermitteln Sie die Frequenz, bei der die Lampe gerade nicht mehr leuchtet.

Fassen Sie Ihre Beobachtungen in einem Satz zusammen.

Versuch 4:

Ersetzen Sie den Widerstand R durch eine Spule mit der Induktivität L.
Vergleichen Sie die Helligkeit der Lampe bei verschiedenen Frequenzen.
Wiederholen Sie den Versuch mit einer Spule mit Eisenkern.

Frequenz	1 Hz	10 Hz	50 Hz	100 Hz	1000 Hz	10000 Hz
L (ohne Eisenkern)	_______	_______	_______	_______	_______	_______
L (mit Eisenkern)	_______	_______	_______	_______	_______	_______

Ermitteln Sie die Frequenz, bei der die Lampe gerade nicht mehr leuchtet.

Fassen Sie Ihre Beobachtungen in einem Satz zusammen.

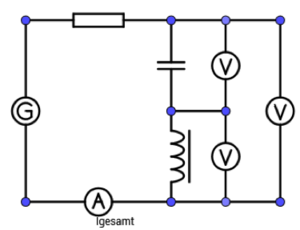
9. Spule und Kondensator im Wechselstromkreis (2)

Geräte

• Labornetzgerät
• Kondensator C = 470 µF
• Kondensator C = 1 µF
• Spule n = 1000 mit Eisenkern
• Glühlampe
• Multimeter als Messgerät für die Frequenz

Versuchsbeschreibung

Die Eigenschaften von Kondensator C und Spule L im Wechselstromkreis sollen quantitativ untersucht werden.

Aus der Gesamtspannung U_g und der Stromstärke I kann der Gesamtwiderstand $Z={\frac {U_{g}}{I}}$ berechnet werden.

Für einen R-C-Kreis gilt: $Z={\sqrt {R^{2}+X_{C}^{2}}}$.
Für einen R-L-Kreis gilt: $Z={\sqrt {R^{2}+X_{L}^{2}}}$, wobei hier der ohmsche Widerstand der Spule mit berücksichtigt werden muss!

Versuch 1: Kondensator (R-C-Kreis)

Ermitteln Sie den Widerstand R der Glühlampe entweder aus den Werten auf dem Sockel oder durch Messung mit dem Multimeter. Dieser Wert wird nachfolgenden als konstant angenommen.

Bauen Sie zunächst die Schaltung nur mit der Glühlampe (ohne Kondensator) auf. Stellen Sie am Funktionsgenerator die Frequenz f = 50 Hz ein und stellen Sie die Ausgangsspannung am Funktionsgenerator so ein, dass die Lampe hell leuchtet.

Schalten Sie jetzt den Kondensator C = 470 µF (wie im Schaltplan gezeigt) dazu.

Messen Sie für Frequenzen von f = 100 Hz bis f = 1000 Hz jeweils die Gesamtspannung U_g und die Stromstärke I. Berechnen Sie Z und X_C und tragen Sie die Werte in ein f-Z-Diagramm ein.

f in Hz	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
Ug in V	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
I in A	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
Z in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
R in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
XC in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______

Formulieren Sie ein Ergebnis.

Versuch 2: Spule (R-L-Kreis)

Ermitteln Sie den Widerstand R der Glühlampe entweder aus den Werten auf dem Sockel oder durch Messung mit dem Multimeter. Dieser Wert wird nachfolgenden als konstant angenommen.

Ermitteln Sie den ohmschen Widerstand R der Spule (n = 1000)

Bauen Sie zunächst die Schaltung mit der Glühlampe mit der Spule (n = 1000 mit Eisenkern) auf. Stellen Sie am Funktionsgenerator die Frequenz f = 50 Hz ein und stellen Sie die Ausgangsspannung am Funktionsgenerator so ein, dass die Lampe möglichst hell leuchtet.

Messen Sie für Frequenzen von f= 100 Hz bis f = 1000 Hz jeweils die Gesamtspannung U_g und die Stromstärke I. Berechnen Sie Z und XL und tragen Sie die Werte in ein f-Z-Diagramm ein.

f in Hz	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
Ug in V	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
I in A	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
Z in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
R in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
XL in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______

Formulieren Sie ein Ergebnis.

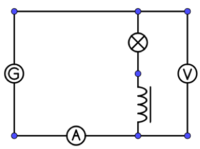
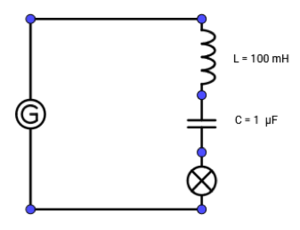
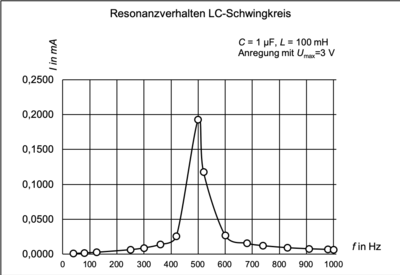
10. Erzwungene Schwingungen

Geräte

• Labornetzgerät
• Kondensator C = 1 µF
• Spule (n = 1000 mit Eisenkern)
• Glühlampe
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

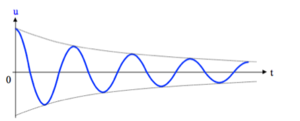
Ein Schwingkreis, der einmalig angeregt wird, führt eine „gedämpfte harmonische Schwingung“ aus.

Für einen dauerhaften Betrieb (z.B. in einem Radiosender) kann der Schwingkreis von außen dauerhaft mit einem Sinusgenerator angeregt werden. Dabei führt der Schwingkreis Schwingungen mit der Frequenz aus, die von außen vorgegeben wird (→ „erzwungene“ Schwingungen). Die durch den Sinusgenerator vorgegeben Frequenz wird als „Erregerfrequenz“ f_err bezeichnet.

Versuch:

Versuch 2

Ein Schwingkreis mit C = 1 µF und L = 100 mH wird durch einen Funktionsgenerator angeregt. Die Glühlampe soll die Stromstärke anschaulich anzeigen. → Wenn die Erregerfrequenz f_err mit der Eigenfrequenz f₀ übereinstimmt, wird die Stromstärke I im Schwingkreis maximal; die Glühlampe leuchtet. In der Physik wird dieser Zustand ( f_err = f₀ ) als Resonanz bezeichnet.

Ermitteln Sie die Frequenz, bei der die Lampe mit maximaler Helligkeit leuchtet.

f₀ = ______ Hz

Aufgaben:

1. Berechnen Sie für f = 100 Hz bis f = 1000 Hz die (theoretischen) Wechselstromwiderstände $X_{L}=\omega \cdot L$ und $X_{C}={\frac {1}{\omega \cdot C}}$ und erstellen Sie eine Wertetabelle.

f in Hz	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
XC in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
XL in Ω	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______

2. Tragen Sie die Werte mit zwei Farben in ein f-X-Diagramm ein.

3. Im Schnittpunkt der beiden Kurven ist X_C = X_L und der Gesamtwiderstand des Schwingkreises hat hier den kleinsten Wert. Leiten Sie aus der Bedingung X_C = X_L die Gleichung für die Eigenfrequenz des Schwingkreises $f_{0}={\frac {1}{2\pi {\sqrt {L\cdot C}}}}$ her.

4. Im Resonanzfall ist die Stromstärke maximal, die Glühlampe leuchtet auf. Berechnen Sie die Resonanzfrequenz f₀ des Schwingkreises.

10.a. Erzwungene Schwingungen – Induktive Kopplung

Geräte

• Labornetzgerät
• Kondensator C = 1 µF
• Spulen (n = 500 und n = 1000 mit Joch)
• Glühlampe
• Multimeter
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

Ein Schwingkreis, der einmalig angeregt wird, führt eine „gedämpfte harmonische Schwingung“ aus.

Für einen dauerhaften Betrieb (z.B. in einem Radiosender) kann der Schwingkreis von außen dauerhaft mit einem Sinusgenerator angeregt werden. Dabei führt der Schwingkreis Schwingungen mit der Frequenz aus, die von außen vorgegeben wird (→ „erzwungene“ Schwingungen). Die durch den Sinusgenerator vorgegeben Frequenz wird als „Erregerfrequenz“ f_err bezeichnet.

Versuch 1:

Versuch 1

Bauen Sie die nebenstehende Schaltung auf. Regeln Sie die Spannung am Funktionsgenerator langsam nach oben, bis die Lampe leuchtet. Erklären Sie den Begriff „induktive Kopplung“.

Versuch 2:

Versuch 2

Bauen Sie die nebenstehende Schaltung auf (C = 1 µF, L(n=1000) = 498 mH)

1. Messen Sie für f = 50 Hz bis f = 500 Hz die Stromstärke I (in mA) im Schwingkreis.
Versuchen Sie möglichst genau die Resonanzfrequenz f_R zu ermitteln.

f in Hz	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
I in mA	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______

2. Tragen Sie die Werte in ein f-I-Diagramm ein.

3. Berechnen Sie die theoretisch zu erwartende Eigenfrequenz des Schwingkreises $f_{0}={\frac {1}{2\pi {\sqrt {L\cdot C}}}}$.
Begründen Sie eventuell auftretende Abweichungen zu den Messwerten

4. Im Resonanzfall ist die Stromstärke maximal. Berechnen Sie die prozentuale Abweichung der gemessenen Resonanzfrequenz fR von der berechneten Eigenfrequenz f₀.

11. Serienresonanz

Geräte

• Labornetzgerät
• Kondensator C = 1 µF
• Spule (n = 1000 mit Eisenkern)
• 2 Multimeter
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

Ein Serienschwingkreis wird mit verschiedenen Frequenzen f zu Schwingungen angeregt. Die Gesamtstromstärke I_g und die Spannung werden gemessen.

Versuch: 1

Versuch 1

Die Ausgangsfrequenz wird auf f = 100 Hz eingestellt.

Die Amplitude am Funktionsgenerator wird auf den maximalen Wert eingestellt.

Bei einer bestimmten Frequenz f_R wird die Stromstärke I minimal.

f in Hz	U in V	I in mA
100
200
300
400
500
600
700
800
900
1000

Versuchen Sie die Resonanzfrequenz f_R möglichst genau zu ermitteln.

f_R = ____________ Hz

Im Resonanzfall ist die Stromstärke am __________ und die Spannung am __________.
Erklären Sie diesen Sachverhalt.

Zeichnen Sie die Resonanzkurve (f-I-Diagramm).

Versuch 2: Serienresonanz

Versuch 2

Stellen Sie am Funktionsgenerator die in Versuch 1 ermittelte Resonanzfrequenz f_R ein.

Messen Sie nacheinander die Gesamtspannung U_Gesamt und die Teilspannungen am Kondensator U_C und an der Spule U_L.

UGesamt	______________
UC	______________
UL	______________

Die Teilspannungen sind ______________ als die Gesamtspannung.

Formulieren Sie ein Ergebnis dieses Experiments.

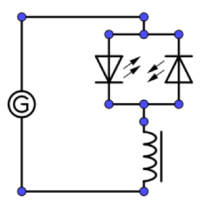
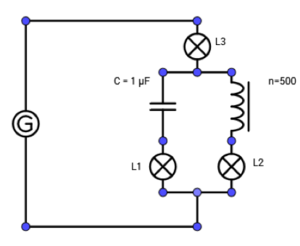
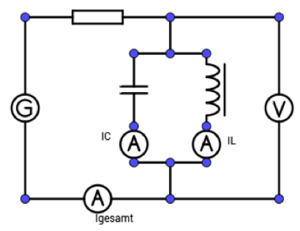
12. Parallelresonanz

Geräte

• Labornetzgerät
• Kondensator C = 1 µF
• Spule n = 500 mit Eisenkern
• 3 Glühlampen
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

Ein Parallelschwingkreis wird durch einen Funktionsgenerator zu erzwungenen Schwingungen angeregt.

Versuch:

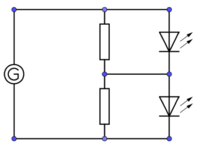
Bauen Sie die Schaltung entsprechenden der nebenstehenden Abbildung auf.

Stellen Sie am Funktionsgenerator für f = 50 Hz die Spannung am Funktionsgenerator so ein, dass die Lampen L₂ und L₃ in etwa gleich hell leuchten.

Verändern Sie jetzt die Frequenz zwischen f = 50 Hz und f = 10 kHz.

Beobachten Sie die Helligkeit der Glühlampen L₁ – L₃.

Notieren Sie ihre Beobachtungen.

Suchen Sie jetzt die Frequenz, bei der die Glühlampen L1 und L2 im Schwingkreis mit der gleichen Helligkeit leuchten. Bei dieser Frequenz liegt der Resonanzfall vor. Formulieren Sie einen Satz über die Helligkeit der Lampen L₁ – L₃ im Resonanzfall.

Beobachten Sie die Helligkeit der Glühlampen für Frequenzen unterhalb der Resonanzfrequenz und für Frequenzen oberhalb der Resonanzfrequenz.

Zu erwartenden Beobachtungen:

• Bei Frequenzen unterhalb der Resonanzfrequenz leuchtet das Lämpchen im Hauptkreis deutlich auf. In der Parallelschaltung fließt der Strom hauptsächlich durch die Spule.
• Im Resonanzfall erreicht die Helligkeit des Lämpchens im Hauptkreis ein Minimum. Die Lämpchen im Spulen- und Kondensatorkreis leuchten gleich hell.
• Für Frequenzen oberhalb der Resonanzfrequenz steigt der Strom in der Hauptleitung wieder an. Das Lämpchen im Kondensatorzweig ist heller als das im Spulenzweig.
• Bei der obigen Anordnung können die Ströme in den Teilzweigen sehr viel größere Amplituden erreichen als der Strom in der Hauptleitung. Man spricht daher beim Parallelkreis auch von Stromresonanz.

Theorie: https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-schwingungen/versuche

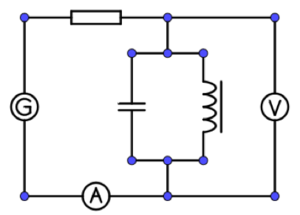
13. Parallelresonanzkreis

Geräte

• Labornetzgerät
• Kondensator C = 1 µF
• Spule n = 1000 mit Eisenkern
• 2 Multimeter
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

Für einen Parallelschwingkreis werden Spannung und Stromstärke gemessen.

Versuch 1

Versuch 1

Bauen Sie die Schaltung entsprechend der nebenstehenden Abbildung auf. C = 1 µF
L = 100 mH
R = 100 Ω

Die Ausgangsfrequenz wird auf f = 100 Hz eingestellt. Die Amplitude am Funktionsgenerator wird auf den maximalen Wert eingestellt.

Bei einer bestimmten Frequenz f_R wird die Stromstärke I minimal.

f in Hz	U in V	I in mA
100
200
300
400
500
600
700
800
900
1000

Versuchen Sie die Resonanzfrequenz f_R möglichst genau zu ermitteln.

f_R = ____________ Hz

Im Resonanzfall ist die Stromstärke am __________ und die Spannung am __________.
Erklären Sie diesen Sachverhalt.

Zeichnen Sie mit Hilfe der Messwerte eine Resonanzkurve (f-I-Diagramm).

Versuch 2: Parallelresonanz

Versuch 2

Stellen Sie am Funktionsgenerator die in Versuch 1 ermittelte Resonanzfrequenz f<su>R ein. Messen Sie nacheinander die Stromstärke I_{Gesamt und die Teilstromstärken IC und IL.}

IGesamt	______________
IC	______________
IL	______________

Die Teilströme sind ______________ als die Gesamtstromstärke.

Formulieren Sie ein Ergebnis dieses Experiments.

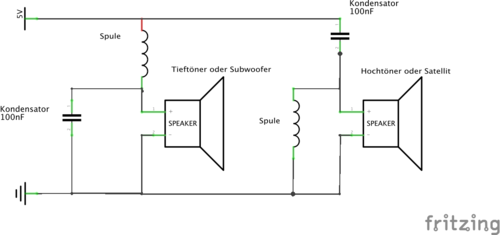
14. Hochpass und Tiefpass

Geräte

• Labornetzgerät
• Kondensator C = 1 µF
• Spule n = 500 mit Eisenkern
• 2 Glühlampen
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

Zweiwege-Lautsprecher mit getrennten Lautsprechern (Hochtöner und Tieftöner) enthalten Schaltungen, die nur Wechselspannungen mit den Frequenzen zu den jeweiligen Lautsprechern weiterleiten, die dort auch gut verarbeitet werden können. Die entsprechenden Schaltungen heißen „Hochpass“ und Tiefpass“ (-Filter).

Versuch 1:

Versuch 1

Bauen Sie die Schaltung entsprechend der nebenstehenden Abbildung auf.

Verändern Sie die Frequenz zwischen f = 50 Hz und f = 10 kHz.

Beobachten Sie die Helligkeit der Glühlampe und notieren Sie diese.

Suchen Sie jetzt die Frequenz, bei der die Glühlampe gerade nicht mehr leuchtet.

Versuch 2:

Versuch 2

Bauen Sie die Schaltung entsprechend der nebenstehenden Abbildung auf.

Verändern Sie die Frequenz zwischen f = 50 Hz und f = 10 kHz.

Beobachten Sie die Helligkeit der Glühlampe und notieren Sie diese.

Suchen Sie jetzt die Frequenz, bei der die Glühlampe gerade nicht mehr leuchtet.

Versuch 3: Hoch- und Tiefpass

Versuch 3

Bauen Sie die Schaltung entsprechend der nebenstehenden Abbildung auf.

Verändern Sie die Frequenzen zwischen f = 50 Hz und f = 10 kHz.

Beobachten Sie die Helligkeit der beiden Glühlampen.

15. R-C-Filter

Geräte

• Labornetzgerät
• Kondensator C = 4,7 µF
• Widerstände R = 100 Ω , R = 1 kΩ
• 2 Multimeter
• Multimeter zur Messung der Frequenz

Versuchsbeschreibung

Filter haben in der Elektrotechnik die Aufgabe bestimmte Frequenzbereiche hervorzuheben oder zu unterdrücken. Wir untersuchen einen Hochpass und einen Tiefpass. Bei einem Hochpass oder Tiefpass (Versuch 12) kann die Spule L auch durch einen Widerstand R ersetzt werden. Die Filter (Hochpass und Tiefpass) bestehen dann aus einem Kondensator C und einem Widerstand R. Diese Art der Schaltung hat Vorteile (Kosten) und Nachteile (Trennung der Frequenzen).

Die Frequenz, bei der X_C = R gilt, wird als Grenzfrequenz f_G bezeichnet.

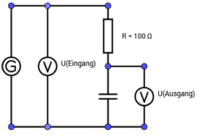
Versuch 1: Tiefpass

Schaltplan zu Versuch 1

Bauen Sie die Schaltung entsprechenden der nebenstehenden Abbildung auf. ( R = 100 Ω, C = 4,7 µF)

In Lehrbüchern wird diese Schaltung häufig anders dargestellt:

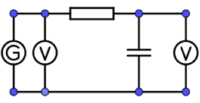
Messen Sie die Eingangsspannung U_E und die Ausgangsspannung U_A für Frequenzen zwischen f = 1 Hz und f = 2 kHz. Berechnen Sie das Verhältnis von U_A/U_E

f in Hz	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
UE in V	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
UA in V	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
UA/UE	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______

Tragen Sie die Werte in ein Diagramm ein, das das Verhältnis von U_A/U_E (Hochachse) über der Frequenz f (Rechtsachse) darstellt.

Ergänzen Sie folgende Sätze:

• Bei hohen Frequenzen ist die Spannung am Kondensator ______________
• Bei niederen Frequenzen hat der Kondensator einen ______________ Widerstand, am Kondensator liegt eine ______________ Spannung an.
• Wir nennen diese Schaltung ______________pass, weil hohe Frequenzen ______________ werden.

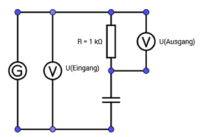
Versuch 2: Hochpass

Schaltplan zu Versuch 2

Bauen Sie die Schaltung entsprechenden der nebenstehenden Abbildung auf. (R = 1 kΩ, C = 4,7 µF)

In Lehrbüchern wird diese Schaltung häufig anders dargestellt:

Messen Sie die Eingangsspannung UE und die Ausgangsspannung UA für Frequenzen zwischen f = 10 Hz und f = 200 Hz. Berechnen Sie das Verhältnis von U_A/U_E

f in Hz	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
UE in V	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
UA in V	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______
UA/UE	_______	_______	_______	_______	_______	_______	_______	_______	_______	_______

Tragen Sie die Werte in ein Diagramm ein, das das Verhältnis von U_A/U_E (Hochachse) über der Frequenz f (Rechtsachse) darstellt.

Ergänzen Sie folgende Sätze:

• Bei hohen Frequenzen ist die Spannung am Kondensator ______________
• Bei niederen Frequenzen hat der Kondensator einen ______________ Widerstand, am Kondensator liegt eine ______________ Spannung an.
• Wir nennen diese Schaltung ______________pass, weil hohe Frequenzen ______________ werden.

Material

Datei:Elektromagnetische Schwingungen AB.zip

Literatur

,,