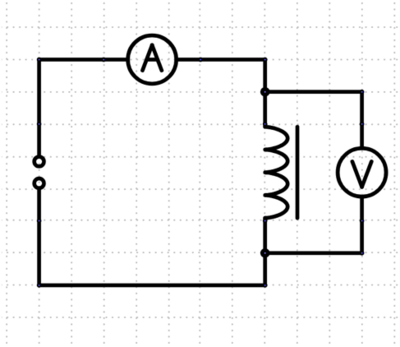
Elektrizitätslehre in der Oberstufe-Gruppenexperimente mit Low-Budget-Geräten
| Diese Experimentieranleitung befindet sich im Entstehen und wurde noch nicht freigeschaltet..
Solltest du Fragen zu dem Thema haben, nimm am besten Kontakt mit dem Autor oder der Autorin auf. |
| Elektrizitätslehre in der Oberstufe-Gruppenexperimente mit Low-Budget-Geräten | |
 Bildunterschrift des Experiments | |
| Kurzbeschreibung | |
|---|---|
| An dieser Stelle soll eine kurze (!) und aussagekräftige Beschreibung formuliert werden. | |
| Kategorien | |
| Elektrizitätslehre, [[:Kategorie:{{{2}}}|{{{2}}}]] | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek I/II |
| Basiskonzept: | System, Wechselwirkung, Energie oder Materie |
| Sonstiges | |
| Durchführungsform | Demoexperiment, Schüler*innen-Experiment, Gruppenexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1, 2, 3 |
| Anspruch des Aufbaus | leicht, mittel, schwer |
| Informationen | |
| Name: | Frank Pozniak, Thomas Beyer, Lilly Pyras |
| Kontakt: | @ |
Häufig zwingt ein knappes Budget gerade die naturwissenschaftlichen Fachbereiche zum Verzicht auf die Anschaffung von kompletten Schülerexperimentiersets für bestimmte Versuche wie z.B. Messungen mit der Hallsonde, Induktivitäts- und Kapazitätsmessungen. An die Stelle dieser Schülerexperimente treten dann oft Demoexperimente oder im schlechtesten Fall die gute alte „Kreidephysik“. Gerade aber das eigene Experimentieren der SuS macht einen großen Teil des Reizes des Fachs Physik aus.
In diesem Artikel wird vorgestellt, wie mit leicht zu beschaffenden und preiswerten Digitalmessgeräten und Komponenten Schülerexperimentiersets zum Themenbereich der Elektrizitätslehre der Oberstufe zusammengestellt werden können. Diese Sets sind teils unterrichtserprobt. Zu allen Versuchen existieren Anleitungen und Arbeitsmaterialien für die Hand der Schülerinnen und Schüler. Geplant sind Experimentierstationen zur Kapazitätsformel eines Plattenkondensators, der Einsatz von Funktionsgeneratoren mit Verstärkerteil für die Behandlung von Wechselstromwiderständen, die Bestimmung von Induktivitäten und deren Abhängigkeiten von der Windungszahl etc., ein kleines Fertigset zur Bestimmung der planckschen Konstanten h und die Festlegung der Flussdichte B durch einen modifizierten Stromwaagenversuch.
Inhaltsverzeichnis
- 1 Steckbrief: Kondensator
- 2 Schülerexperiment: Kondensator
- 3 Arbeitsauftrag : Das Laden und Entladen eines Kondensators
- 4 Experimentierauftrag: Das Magnetfeld einer langen Spule
- 5 Arbeitsblatt: Magnetische Flussdichte
- 6 Schülerexperiment: Die Kapazität mit LCR-Meter
- 7 Messungen mit dem Funktionsgenerator
- 7.1 Der Anschluss des Frequenzgenerators
- 7.2 Die Frequenzabhängigkeit des Wechselstromwiderstandes eines Kondensators
- 7.3 Abhängigkeit des kapazitiven Widerstandes von der Kapazität
- 7.4 Beispiel: Messwerte für den C- I- Zusammenhang und die Auswertung
- 7.5 Die Frequenzabhängigkeit des Wechselstromwiderstandes einer Spule
- 7.6 Abhängigkeit des induktiven Widerstandes von der Induktivität
- 8 Bezugsquellen
- 9 Dateien
- 10 Literatur
- 11 Siehe auch
Steckbrief: Kondensator
Kondensatoren speichern Ladungen. Sie finden Anwendung in verschiedenen Bereichen der Technik:
__________________________________________________________________________________________
Kenngrößen: Kapazität C = ____________________; Q = ____________________; ...
_________________________________________________________________________; U = Spannung
Einheiten: [C] = 1 F = 1 ______________
Die Kapazität 1 F bedeutet, dass bei einer Spannung von 1 V ____________________ gespeichert wird.
Bei Plattenkondensatoren kann man aus den Abmessungen des Flächeninhalts der Platten und des Abstands der Platten die Kapazität bestimmen: C = ____________________
Wir untersuchen den Kondensator als Ladungsspeicher
Skizziere in einem Diagramm den vermutlichen Helligkeitsverlauf über der Zeit.
Untersuche die Entladung des Kondensators in der Zeit. Zeichne ein Diagramm der Stromstärke über der Zeit und ermittle die gesamte gespeicherte Ladungsmenge Q. Vergleiche deinen Wert mit dem durch C = Q/U berechneten Ergebnis.
Schülerexperiment: Kondensator
Theorie
Anordnungen aus zwei Leitern, die durch einen Isolator getrennt sind, heißen Kondensatoren. Aufgrund ihrer Fähigkeit, Ladung und Energie zu speichern, werden sie vielfältig eingesetzt. Die Kapazität C gibt an, wie viel Ladung der Kondensator bei einer bestimmten Spannung speichern kann:
Der Quotient verändert sich für einen bestimmten Kondensator nie! Seine Kapazität ist also durch seine Bauart festgelegt und daher konstant. Die Einheit der Kapazität ist Farad (F).
1 Farad ist eine sehr große Kapazität. Kondensatoren mit dieser Kapazität können bei einer Spannung U = 1V die Ladung Q = 1C speichern. Kondensatoren in technischen Geräten haben oft wesentlich geringere Kapazitäten, z.B.
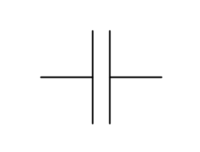
Schaltzeichen eines Kondesators
Gruppenarbeit – je Tisch eine Gruppe
Legen Sie einen Zeitwächter fest und einen Protokollführer, der stellvertretend für die Gruppe sein Protokoll am Stundenende abgibt. Sie haben 45 Minuten Zeit für Versuchsdurchführung, Protokoll und Auswertung.
Es ist bekannt, dass die Kapazität C eines Kondensators nur von seiner Bauart abhängt. Im vorliegenden Fall bilden zwei Rechtecke aus Aluminiumfolie die beiden Elektroden (entspricht den „Platten“). Sie sind in Laminierfolie eingschweist, wobei die Folienschicht auf der Vorder- bzw. Rückseite der Aluminiumfolie je 125 μm dick ist.
Legt man diese „Sandwiches“ aufeinander, entsteht ein Kondensator. Die beiden Elektroden werden hier durch die Kunststoffbeschichtungen isoliert. Diese Schicht zwischen den zwei Elektroden nennt man Dielektrikum, siehe Schnittdarstellung rechts.
Aufgaben
- Messen Sie mit dem LCR-Messgerät die Kapazität ihres Kondensators: C1 =____________________________
- Überlegen Sie sich wie Sie die „Bauart“ ihres Kondensators verändert werden kann:
- Stellen Sie auf der Rückseite zwei Hypothesen auf, von welchen Größen die Kapazität ihres Kondensators bestimmt wird. Hinweis: Betrachten Sie genau die zur Verfügung gestellten Utensilien.
- Tragen sie diese Größen in die Skizze auf der Rückseite ein.
- Formulieren Sie jeweils eine Vermutung, wie diese Größe die Kapazität beeinflusst (je-desto-Beziehung).
Hypothesen
Hypothesen:
a)
Größe 1: ___________________
Vermutung: __________________________________________________
b)
Größe 2: ___________________
Vermutung: ______________________________________________________
Messkampagne
Überprüfen Sie Ihre Hypothesen durch geeignete Experimente am Kondensator:
- Halten Sie eine der beiden Größen konstant und variieren sie die andere mindestens zwei mal.
- Halten Sie nun die andere Größe konstant und variieren die erstere mindestens zwei mal.
| Hypothese a | Hypothese b | ||
| konstant gehaltene Größe: _______ | konstant gehaltene Größe: _______ | ||
| veränderliche Größe _______ in _______ | gemessene Kapazität in _______ | veränderliche Größe _______ in _______ | gemessene Kapazität in _______ |
| _______________________________ | _______________________________ | _______________________________ | _______________________________ |
| _______________________________ | _______________________________ | _______________________________ | _______________________________ |
| _______________________________ | _______________________________ | _______________________________ | ________________________________ |
Auswertung
Stellen Sie die Messwerte grafisch in den Koordinatensystemen dar. Beschriften Sie die Achsen. Zeichnen Sie Ausgleichsgraphen ein.
Interpretieren Sie Ihre Ergebnisse. Begründen Sie, ob sich Ihre Hypothesen bestätigt haben. _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________
Weiterführende Aufgabe für Schnelle
Stellen Sie eine Vermutung für eine mathematische Formel für die Kapazität eines Kondensators auf. Überprüfen Sie Ihre Formel anhand Ihrer Messwerte.
Plenum
Präsentieren Sie Ihre Ergebnisse vor der Klasse in geeigneter Form.
Arbeitsauftrag : Das Laden und Entladen eines Kondensators
- Bauen Sie die gezeigte Schaltung auf. Beachten Sie dabei, dass sowohl der Kondensator als auch die LED´s gepolte Bauelemente sind. Schließen Sie eine Spannungsquelle 6 V an (+ an orange).
- Bringen Sie den Drahtschalter nun in die Stellung „Aufladen“ und beobachten Sie die LED 1 (oben) .
- Stellen Sie den Verlauf der Helligkeit der LED über der Zeit grafisch dar. Dies müssen Sie aus der Beobachtung ableiten.
- Bringen Sie den Drahtschalter nun in die Stellung „Entladen“ und beobachten Sie die LED 2 (unten). Wiederholen Punkt 3 für die Entladung. Klemmen Sie dazu die Spannungsquelle ab.
- Zeichnen Sie ein Schaltbild der gezeigten Schaltung und markieren Sie den Verlauf des Stroms während des Aufladens und des Entladens (verschiedenfarbig).
- Entfernen Sie den linken Kondensator. Wiederholen Sie die Schritte 2 und 4. Beschreiben Sie ihre Beobachtung.
- Setzen Sie den Kondensator wieder ein und ersetzen Sie die Leuchtdioden durch je ein Strommessgerät und die Widerstände durch Widerstände der Größe R = 22 kΩ Messen Sie die Stromstärke und die zugehörige Zeit beim Aufladen, erfassen Sie die Messwerte in einer Tabelle und werten Sie diese grafisch aus.
- Verfahren Sie ebenso beim Entladen.
- Bestimmen Sie die Halbwertzeit der Entladung und bestätigen Sie die Gleichung .
- Bestimmen Sie für die Aufladekurve die Fläche unter der Kurve durch geeignete Flächenzerlegung. Welche physikalische Größe wird hier beschrieben?
- Diese Schaltung kann als Kurzzeitmesser benutzt werden. Beschreiben Sie, wie das funktionieren könnte.
Experimentierauftrag: Das Magnetfeld einer langen Spule
- Bestimmen Sie mit der Linken-Hand-Regel den Verlauf des Magnetfeldes in der Spule und außenhalb der Spule. Zeichnen Sie den Verlauf in das Bild.
- Untersuchen Sie mit der Hallsonde die Flussdichte B abhängig von dem Ort x , d.h. fahren Sie mit der Sonde durch das Spuleninnere und erfassen Sie die Werte.
- Stellen Sie B(x) grafisch dar und formulieren Sie ihre Erkenntnis.
- Untersuchen Sie nun den Zusammenhang zwischen Stromstärke I in den Spulenwindungen und der Flussdichte B in der Spule (Messort Spulenmitte). Erstellen Sie auch hier eine Grafik und formulieren Sie begründet den mathematischen Zusammenhang.
- Verwenden Sie nun die zusammendrückbare Spule. Variieren Sie die Länge der Spule und erfassen Sie bei konstanter Stromstärke jeweils die Flussdichte B in der Spulenmitte. Werten Sie hier den Zusammenhang zwischen B und der Windungsdichte n/l grafisch und mathematisch aus.
- Formulieren Sie nun auf Grundlage ihrer Messergebnisse eine mathematische Formel über die Abhängigkeit der Flussdichte B von Stromstärke, Windungszahl und Länge der Spule. Hinweis: Erfassen Sie in jedem Experiment alle konstant gehaltenen Größen (Länge / Windungszahl / Stromstärke)
- Setzen Sie nun 3 gleiche Experimentierspulen zu einer langen Spule zusammen und testen Sie die gefundene Gesetzmäßigkeit auf ihre Gültigkeit.
- Stecken Sie in die Spulen Eisenkerne und messen Sie zwischen zwei Kernen die Flussdichte. Vergleichen Sie die Werte mit der Anordnung ohne Eisenkern. Begründen Sie das Ergebnis.
- Legen Sie in die lange Spule einen Kompass und richten Sie die Anordnung in Ost-West-Richtung aus. Lassen Sie nun durch die Spule einen regelbaren Strom fließen. Messen Sie die Stromstärke, bei der die Nadel gerade in Richtung Nord-Ost oder Nord-West zeigt. Mit diesem Wert der Stromstärke und den Daten der Spule können Sie die Stärke des Erdmagnetfeldes berechnen. Führen Sie die Rechnung aus und vergleichen Sie den Wert mit einer Angabe z.B. aus dem Internet.
Arbeitsblatt: Magnetische Flussdichte
Kraft auf stromdurchflossene Leiter im Magnetfeld
Experimentelle Beobachtung
Ein elektrischer Leiter verläuft senkrecht zur Feldrichtung eines magnetischen Feldes. Fließt durch diesen Leiter ein Strom, so erfährt er eine Kraft, die sowohl senkrecht auf dem Leiter als auch senkrecht auf der Feldrichtung steht.
Aufgabe 1
Zeichne zunächst nur in der schrägen Perspektive mit drei verschiedenen Farben:
- die Feldlinien des magnetischen Feldes (B),
- die Richtung des Stromflusses (I, Achtung: die technische Stromrichtung verläuft vom elektrischen Plus- zum Minuspol),
- die Richtung der auftretenden Kraft (F) ein.
Leite daraus den Namen der Regel unten ab („Linke-Hand-Regel“ oder „Rechte-Hand-Regel“)
Die _______ -Hand-Regel: Der Daumen zeigt die (technische) Stromrichtung an, der Zeigefinger die Richtung des magnetischen Feldes und der Mittelfinger die Richtung der Kraftwirkung.
Aufgabe 2
Finde deine Vierergruppen (evtl. eine Fünfergruppe), indem du dein Zeichen (ganz oben, neben dem Datum) richtig einer Gruppe zuordnest.
Bestimmt einen Zeitwächter, der auf die Einhaltung der Arbeitszeit achtet.
Aufgabe 3 – Bestimmung der Richtung des magnetischen Feldes (8 Minuten)
- Auf beiden Seiten der Führungsrinne sind Flachmagnete aufgeklebt (nicht entfernen!). Wo liegen die Nord- und Südpole bei Flachmagneten?
- Bestimme die Lage der Magnetpole und zeichne diese in die Schnittdarstellung ein. Dabei ist die Blickrichtung zu beachten (wenn man von der anderen Seite in die Rinne schauen würde, würde sich alles in der Skizze umkehren).
- Ergänze nun noch 2-3 Feldlinien des homogenen Magnetfeldes im Inneren der Rinne.
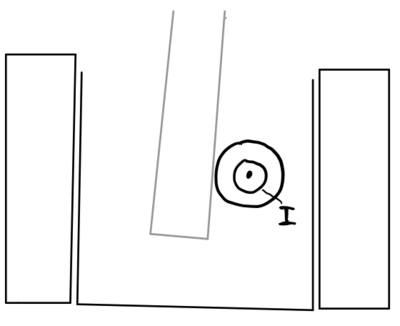
Abbildung: Schnittdarstellung durch den Kanal und den Leiterdraht, in dem ein Stromfluss I eingezeichnet ist.
Aufgabe 4 – Kraftwirkung (5 Minuten)
Bestimme mit Hilfe der Rechte-Hand-Regel die Richtung der Kraft auf den Drahtabschnitt im Kanal, wenn der Strom in die eingezeichnete Richtung fließt. Zeichne FDraht mit einem Kraftpfeil oben in Abb. 1 ein.
Da Kräfte niemals allein auftreten (Wechselwirkungsgesetz), muss eine zweite gleich große, aber entgegengesetzte Kraft auf den Kanal FKanal wirken. Zeichne FKanal in Abb. 1 ein.
In der Folge soll diese Kraft experimentell aus der eben abgeleiteten Änderung der Gewichtskraft des Kanals bestimmt werden. Dazu muss jeweils die Angezeigte Masse (in g) in eine Kraft umgerechnet werden. Man nutze und beachte die Einheitenumrechnung (Gramm in Kilogramm).
Beispiel: Es wird angezeigt: -0,8 g -> Die Waage registriert eine geringere Gewichtskraft als vorher und gibt dies als „leichter werdende Masse“ aus. Ursache ist eine nach oben gerichtete Kraft von N, die dazu gekommen ist.
Aufgabe 5 – Versuchsaufbau: Vor Inbetriebnahme vom Lehrer überprüfen lassen! (5 Min.)
Baue den Versuch wie auf dem nächsten Blatt in Abbildung 2 dargestellt auf.
!Achtung!: Vor dem Einschalten ist die regelbare Spannung auf Null einzustellen. Die Verbindungskabel sind am Stromversorgungsgerät an den regelbaren Gleichstromanschlüssen anzuschließen. Nun vorm Einschalten den Aufbau vom Lehrer abnehmen lassen!

Abbildung: Skizze des Versuchsaufbaus
Aufgabe 6 – 1. Messreihe zur Stromstärkeabhängigkeit der Kraft (15 Minuten)
Miss nun die Abhängigkeit der Kraft von der Stromstärke für eine gegebene Leiterlänge, z.B. 5 cm. Der Drahtabschnitt sollte dabei mittig in der Rinne gehalten werden und nicht aus der Rinne hinausschauen (weder links, noch rechts, noch oben).
- Die Leiterschleife ist dabei so zu halten, dass der Kanal nicht berührt wird (!), da sonst die Waage die Gewichtskraft der Leiterhalterung misst. Der Leiter und seine Aufhängung dürfen den Kanal an keiner Stelle berühren.
- Vergewissere dich, dass die Spannung am Stromversorgungsgerät auf Null steht und das Amperemeter auf den größtmöglichen Messbereich (6000 mA) eingestellt und richtig angeschlossen ist.
- Schalte die Waage ein und kalibriere sie ggf. noch auf Null („tare“) – den Kanal wie gesagt nicht berühren.
- Schallte das Stromversorgungsgerät am Kippschalter ein und regle die Spannung vorsichtig hoch, bis das Amperemeter 2,5 Ampere anzeigt. Ließ den von der Waage angezeigten Wert ab und regle dann schnell die Spannung wieder herunter und schalte das Gerät aus (Erhitzung des Drahtes kann den Leiter sonst beschädigen).
Wiederhole den Versuch für 5 Ampere und noch einmal bei umgekehrter Stromrichtung (also -5 Ampere -> Amperemeter umstecken, da dieses nur positive Stromstärken anzeigen kann).
Tabelle: Messwerte und berechnete Kraft für eine geg. Leiterlänge l.
| Leiterlänge l in m | Stromstärke I in A | Massenänderung in kg | Kraft F in N |
|---|---|---|---|
| ____________ | 0 (ohne Stromfluss) | ____________ | ____________ |
| ____________ | 2,5 | ____________ | ____________ |
| ____________ | 5 | ____________ | ____________ |
| ____________ | -5 (andere Richtung) | ____________ | ____________ |
Aufgabe 7 (8 Minuten)
Wähle in folgendem Diagramm eine passende Einteilung für die Ordinate. Trage die Messwerte dann in das Diagramm ein.
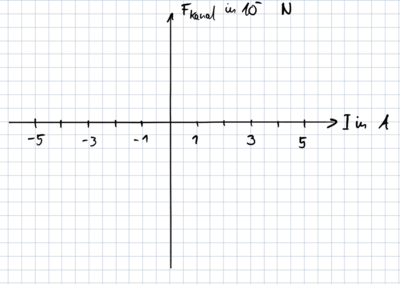
Diagramm: Abhängigkeit der Kraft F von der Stromstärke I
Formuliere den mathematischen Zusammenhang von Kraft F und Stromstärke I.
_____________________________________________________________________
Aufgabe 8 - 2. Messreihe zur Leiterlängenabhängigkeit der Kraft (10 Minuten)
Übernimm die Messwerte für die 1. Leiterlänge und wiederhole den Versuch mit mindestens einer anderen Leiterlänge.
Tabelle: Messwerte für verschiedene Leiterlängen l.
| Leiterlänge l in m | Stromstärke I in A | Massenänderung in kg | Kraft F in N |
|---|---|---|---|
| ____________ | 5 (Übernahme aus Tabelle 1) | ____________ | ____________ |
| ____________ | 5 | ____________ | ____________ |
| ____________ | 5 | ____________ | ____________ |
| 0 (kein Leiter) | 5 | 0 | 0 |
Aufgabe 9 (8 Minuten)
Wähle in folgendem Diagramm eine passende Einteilung für die Ordinate. Trage die Messwerte dann in das Diagramm ein.
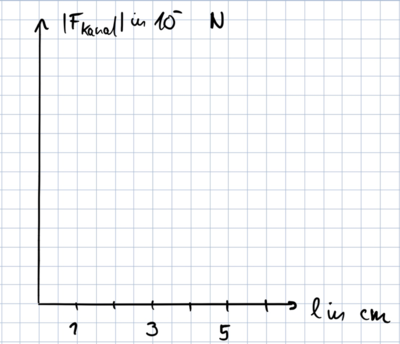
Diagramm: Abhängigkeit des Betrags der Kraft F von der Leiterlänge l.
Formuliere den mathematischen Zusammenhang vom Betrag der Kraft F und Leiterlänge l.
_____________________________________________________________________
Zusatz
Überlege, wie sich die Richtung des Magnetfeldes bei gegebenem Stromfluss ändern lässt.
Erläutere dein experimentelles Vorgehen.
Formuliere eine Hypothese (=Vermutung), welche Auswirkung das auf die zu messende Kraft hat, begründe ggf. mit der Rechte-Hand-Regel.
Überprüfe deine Vermutung mit einem Experiment.
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
--- Für die gemeinsame Auswertung – noch nicht bearbeiten ---
Für die Kraft F auf einen vom Strom I durchflossenen Leiter der Länge l, der senkrecht zu den Feldlinien in einem Magnetfeld der Flussdichte B verläuft, gilt:
, wobei I (und l)
Die relativen Richtungen von Kraft, Stromfluss und Feld lassen sich über die Rechte-Hand-Regel bestimmen.
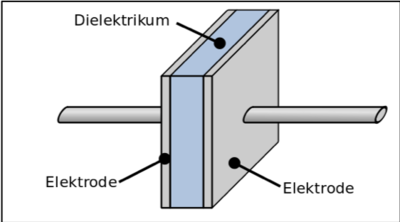
Durch umstellen erhält man schließlich die Definitionsgleichung für den Betrag der magnetischen Flussdichte B:
Die Einheit von B ist 1 Tesla:
Aufgabe 8
Bestimme die mag. Flussdichte des Feldes im Kanal der Experimentieranordnung und vergleiche dein Ergebnis mit typischen Flussdichten für Magnete in der folgenden Tabelle.
Tabelle: Einige Beispiele magnetischer Flussdichten in Natur und Technik:
| B in T | Beispiel |
|---|---|
| Erdmagnetfeld in Deutschland | |
| 0,1 | Handelsüblicher Hufeisenmagnet |
| 1 - 1,5 | NdFeB-Magnete (Neodym-Eisen-Bor), die derzeit stärksten Dauermagnete |
| 8,6 | Supraleitende Dipolmagnete beim größten Teilchenbeschleuniger (LHC) |
| Magnetfeld auf einem Neutronenstern |
Schülerexperiment: Die Kapazität mit LCR-Meter
Die Kapazität eines Plattenkondensators
Sie kennen bereits die Definition der Kapazität C=Q/U. Ein einfacher Plattenkondensator hat natürlich auch eine feste Kapazität. Wir lesen also ab: Die gespeicherte Ladungsmenge Q ist direkt proportional der angelegten Spannung. Bildlich gesprochen: Wir können auf den Kondensator mehr Ladungen „pressen“, wenn der Druck (hier: die Spannung) größer ist.
Nun sollen Sie eine weitere Frage beantworten: Wie hängt dieses Speichervermögen (also die Kapazität) für Ladungen von der Bauform des Kondensators ab? Schließlich wollen wir ja bei einer gegebenen Spannung möglichst viele Ladungen speichern, wir wollen also eine möglichst große Kapazität unseres Plattenkondensators.
Unser Experimentierset
- 1 LCR-Meter
- 2 kaschierte Aluminiumfolien mit Anschlüssen
- Kopierpapier als „Füllung für unseren Kondensator
- Pappstreifen als Abstandshalter für die Folien
Aufgaben
1. Stellen Sie begründete Vermutungen darüber auf, wie die Kapazität von der Fläche A , dem Plattenabstand d und dem „Füllmaterial“ Kopierpapier abhängt.
2. Testen Sie anschließend ihre Vermutungen mit dem LCR-Meter.
3. Untersuchen Sie nun quantitativ die Abhängigkeiten der Kapazität...
...von der Plattenfläche
...vom Abstand der Platten
...von der Menge des Füllmaterials
4. Erfassen Sie die Messwerte in geeigneten Messtabellen. Vergessen Sie dabei nicht, die konstant gehaltenen Größen zu notieren.
5. Stellen Sie nun die gemessenen Abhängigkeiten C von A und C von d grafisch dar.
6. Geben Sie einen möglichen mathematischen Zusammenhang der Messgröße zur Kapazität an.
Messungen mit dem Funktionsgenerator
Der Funktionsgenerator NTL ist eine Spannungsquelle, mit der wir Spannungen verschiedener Form (Sinus, Dreieck, Rechteck) und verschiedener Frequenz (0,1 Hz bis 100 kHz) an elektrische Schaltungen anlegen können.
Da unser geliebtes Polytestmessgerät nur auf Sinus- Spannungen vorbereitet ist, wählen wir für alle Messungen mit diesem Gerät die Funktionsstellung (2) Sinus. Der Frequenz- Feinregler (3) sollte vor der Messung auf 0,2 stehen.
Bevor die Messung beginnt, sollte am Poti (4) zur Regelung der Amplitude der Spannung ein mittlerer Wert eingestellt werden.
Der Anschluss des Frequenzgenerators
In Schwarz: 12 V Wechselspannung
Die für Untersuchungen zu nutzende Spannung kommt aus den beiden Kontakten unten rechts (mit blauem und rotem Kabel versehen).
Die Frequenzabhängigkeit des Wechselstromwiderstandes eines Kondensators
Wähle den Kondensator mit der Kapazität C = 4 μF.
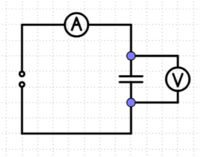
- Baue folgende Schaltung auf.
- Miss mit den Polytest-Messgeräten die Spannung und die Stromstärke bei jeweils einer Frequenz der sinusförmigen Wechselspannung.
- Stelle für den ersten Versuch die Frequenz 1 Hz ein. Miss U und I.
- Wiederhole für 10 Hz und n·10 Hz mit n ϵ {1; 5} jeweils die Spannungs- und Strommessung.
- Berechne für jede Frequenz den Wechselstromwiderstand.
- Zeichne anschließend ein Diagramm, in welchem die Abhängigkeit des Wechselstromwiderstandes von der Frequenz dargestellt ist.
Abhängigkeit des kapazitiven Widerstandes von der Kapazität
Untersuchen Sie in diesem Teilexperiment, wie der fließende Strom in einer Wechselspannungsschaltung von der Kapazität des Kondensators abhängt.
Vorbereitung
- Stellen Sie eine Vermutung zur Abhängigkeit des Widerstandes von der Kapazität auf.
- Schlussfolgern Sie auf den Zusammenhang I = f(C).
- Geben Sie die in Europa benutzte Wechselspannungsfrequenz an.
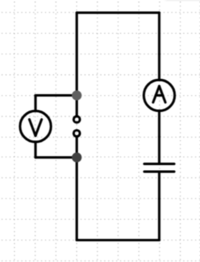
Schaltung
Bauen Sie die Schaltung auf. Kapazitäten erreicht man nach dem Gesetz für Reihen- bzw. Parallelschaltung, das in der Formelsammlung zu finden ist.
Messung
Verändern Sie die Kapazität und messen Sie bei konstanter Spannung U = 6 V jeweils die Stromstärke. Notieren Sie Ihre Messwerte in folgender Tabelle.
| C in | 1 | 4 | 20 | 100 | 200 | _______ | _______ | 4700 |
| I in | _______ | _______ | _______ | _______ | _______ | _______ | _______ | _______ |
Auswertung
- Zeichnen Sie ein C- I- Diagramm für die Messung.
- Berechnen Sie nach dem Ohmschen Gesetz den jeweiligen Widerstand der Schaltung.
- Geben Sie eine Vermutung über den Zusammenhang R~ –C an.
- Bestätigen Sie diese Vermutung rechnerisch.

Abb.: Möglicher Aufbau der Schaltung mit dem Frequenzgenerator(insbesondere der linke Teil ist wichtig).
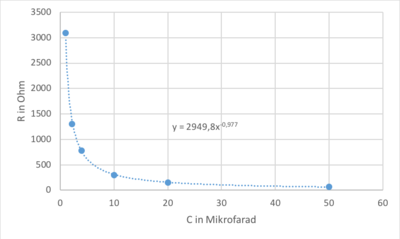
Beispiel: Messwerte für den C- I- Zusammenhang und die Auswertung
| C in μF | U in V | I in mA | R in Ω |
|---|---|---|---|
| 4 | 6,5 | 8,3 | 783 |
| 1 | 6,5 | 2,1 | 3095 |
| 20 | 6,5 | 42 | 155 |
| 50 | 6,5 | 96 | 67,7 |
| 10 | 6,5 | 22 | 295 |
| 2,2 | 6,5 | 5,0 | 1300 |
- C- I- Diagramm siehe unten
- Siehe Spalte 4
- Vermutung
- Werte für
| 3,132 ms | 3,095 ms | 3,1 ms | 3,385 ms | 2,95 ms | 2,86 ms |
Diese Werte deuten auf ein festes Resultat hin und bestätigen deshalb die Vermutung.
So gilt ergibt sich für . Dieser Wert kommt nach der Tabelle in 4. nicht unbekannt vor.
Die Frequenzabhängigkeit des Wechselstromwiderstandes einer Spule
Wähle die Spule mit der Windungszahl 500.
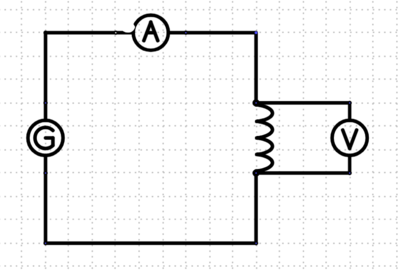
- Baue folgende Schaltung auf.
- Miss mit den Polytest- Messgeräten die Spannung und die Stromstärke bei jeweils einer Frequenz der sinusförmigen Wechselspannung.
- Stelle für den ersten Versuch die Frequenz 1 Hz ein. Miss U und I.
- Wiederhole für 10 Hz und 10n Hz mit n ϵ {1; 5} jeweils die Spannungs- und Strommessung.
- Berechne für jede Frequenz den Wechselstromwiderstand.
- Zeichne anschließend ein Diagramm, in welchem die Abhängigkeit des Wechselstromwiderstandes von der Frequenz dargestellt ist.
Abhängigkeit des induktiven Widerstandes von der Induktivität
Untersuchen Sie in diesem Teilexperiment, wie der fließende Strom in einer Wechselspannungsschaltung von der Induktivität der Spule abhängt.
Vorbereitung
- Stellen Sie eine Vermutung zur Abhängigkeit des Widerstandes von der Induktivität auf.
- Schlussfolgern Sie auf den Zusammenhang I = f(L).
- Geben Sie die in Europa benutzte Wechselspannungsfrequenz an.
Schaltung
- Bauen Sie die rechts sichtbare Schaltung auf. Induktivitäten erreicht man mit:
- Spule mit 500 Windungen, luftgefüllt,
- Spule mit 500 Windungen mit I- Kern gefüllt,
- Spule mit 500 Windungen auf geschlossenem Kern und
- Spule mit 1000 Windungen auf geschlossenem Kern.
Messung
Verändern Sie die Induktivität und messen Sie bei konstanter Spannung von ca. U = 6 V jeweils die Stromstärke. Notieren Sie Ihre Messwerte in folgender Tabelle.
| L | _______ | _______ | _______ | _______ | _______ | _______ | _______ | _______ |
| I in | _______ | _______ | _______ | _______ | _______ | _______ | _______ | _______ |
Auswertung
- Geben Sie für die Messung eine Abhängigkeit der Stromstärke von der Induktivität an.
- Berechnen Sie nach dem Ohmschen Gesetz den jeweiligen Widerstand der Schaltung.
- Geben Sie eine Vermutung über den mathematischen Zusammenhang R~ –L an.
Bezugsquellen
Bezeichnungen:
- Bauteiletester
- Funktionsgenerator Bausatz
- Neodymmagnete ( manchmal auch „rare earth“ Magnete)
- Hallsensor für Arduino
- Breadbord
- Step-up bzw. step down Regler, oder kurz DC-DC-Regler
- Verstärkermodule Arduino
- Allgemein ist das Stichwort „Elektronik basteln“ oder „Elektronik DIY“ zielführend
Folgende Seiten sind hilfreich:
- Amazon.de
- ebay.de
- pollin elektronik (häufig gute Sonderangebote)
- www.wish.com (hier muss man allerdings einen Account anlegen)
- www.geek.com
Dateien
Datei:Unterrichtsmaterialien Elektrizität.zip
Literatur


















![{\displaystyle [B]={\frac {1N}{A\cdot m}}=1T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c07175197b2bdba75a96174343d9c049cc8a45eb)