Elektrischer Schwingkreis

Elektrischer Schwingkreis
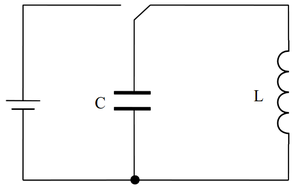
Grundaufbau mit Cassy-Modul
Kurzbeschreibung
Messung des Strom- und Spannungsverlaufs am elektr. Schwingkreis
Kategorien
Elektrizitätslehre Induktion
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	System
Sonstiges
Durchführungsform	Lehrerdemoexperiment, Schülerdemoexperiment, (evtl. Schülergruppenexperiment)
Anspruch des Aufbaus	leicht bis mittel
Informationen
Name:	David Winderlich
Kontakt:	${\text{d.winderlich}}$@${\text{gmail.com}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Franz Boczianowski

Der elektrische (auch elektromagnetische) Schwingkreis ist eine elektrische Schaltung, bei der ein Kondensator der Kapazität C mit einer Spule der Induktivität L miteinander so verbunden sind, dass sich der Kondensator periodisch auf- und entladen kann. Durch ständigen Austausch der Energie zwischen dem elektrischen Feld des Kondensators, sowie dem magnetischen Feld der Spule liegt abwechselnd eine hohe Spannung bzw. Stromstärke vor. Hält man ihren Verlauf fest, erhält man eine Schwingungskurve, wie man sie von harmonischen Oszillatoren kennt.

Den Schülern soll durch dieses Experiment näher gebracht werden, dass das Phänomen der bereits bekannten mechanischen Schwingungen in ähnlicher Form auch in der Elektrizitätslehre bei elektrischen Schaltungen zu finden ist. Genauer gesagt wird die Frequenz des Schwingkreises in Abhängigkeit von veränderbaren Größen (Induktivität, Kapazität) berechnet, indem man die Spannung bzw. Stromstärke misst.

Didaktischer Teil

benötigte Vorkenntnisse der Schüler

• Induktivität einer Spule, Selbstinduktion
• Kondensator als Ladungs-/Energiespeichers , Auf- und Entladen
• Kenntnis über periodische Schwingung bspw. aus der Mechanik
• evtl. Lösen von Differentialgleichungen

Punkt 1 und 2 sind notwendig, um die einzelnen Vorgänge des Experiments zu verstehen. Sie sollten bereits im vorangegangenen Unterricht Thema gewesen sein. Punkt 3 dient dazu, später eine Brücke zwischen den Themengebieten zu schlagen, beziehungsweise den Schülern das Verstehen des Experiments zu vereinfachen, da sie es mit bereits Gelerntem vergleichen können. Punkt 4 spielt nur dann eine Rolle, wenn man die Theorie der Thomsonschen Schwingungsgleichung nicht vorgeben will, sondern selbst im Unterricht herleitet.

Einsatzmöglichkeiten des Experiments

Als Grundlage für elektromagnetische Schwingungen

Hat man als Lehrer z.B. vor Funktechnik (Antenne, Radio,...) zu behandeln, bietet sich dieses Experiment als Einführung in elektromagnetische Schwingungen an. Sind die Vorkenntnisse vorhanden, ist dieses Experiment leicht zu verstehen und baut eine Grundlage auf, die später bei der Behandlung des Herz´schen Dipols vorhanden sein muss. Der Versuch kann zum Verfestigen und zur Veranschaulichung nach der Theorie in den Unterricht eingeführt werden. So überprüft man beispielsweise die Gültigkeit der Thomsonschen Schwingungsgleichung, die man zuvor kennengelernt hat. Es ist jedoch auch möglich, den Versuch vor der Klasse vorzuführen, ohne vorher das neue Thema zu nennen. So gibt man den Schülern den Anreiz, das Ergebnis des Experiments selbst mithilfe bereits Gelerntem zu deuten und auf diese Weise ihr Interesse für dieses Themengebiet zu wecken.

Als Schülervortrag

Dieses Experiment ist hervorragend als Schülervotrag geeignet. Da das Thema nicht allzu kompliziert ist, kann es im Eigenstudium erlernt werden. Statt selbst elektromagnetische Schwingungen in den Unterricht einzuführen, überlässt man es auf diese Weise einem Schüler.

Als Übungsexperiment

Experimente bilden einen Großteil des Umfangs in der Schulphysik. Auch in späteren Bildungsverlauf ist die richtige Vorgehensweise beim Experimentieren wichtig. Deswegen muss es in der Schule immer wieder trainiert werden. Darüber hinaus ist es bei Schülern eine der bevorzugten Unterrichtsaktivitäten. Die verwendeten Bauteile für die Schaltung sollten in großem Maße in der Schule vorhanden sein (Ausnahme: Oszilloskop/Cassy). Es bietet sich hier also an, die Schüler in Gruppen arbeiten und ein Protokoll anfertigen zu lassen. Ebenso kann man jeder Gruppe unterschiedliche Kombinationen aus Kapazitäten und Induktivitäten zu geben, damit sie am Ende ihre Ergebnisse in der Klasse zusammentragen können. Sollten zu wenige Geräte zur Aufnahme der Messwerte vorhanden sein kann man diese von Gruppe zu Gruppe herumreichen. Ist die Schaltung korrekt aufgebaut, sollte die Aufnahme nur wenig Zeit in Anspruch nehmen. Eine andere Lösung wäre hier das Arbeiten mit einem Steckbrett, auf das jede Gruppe ihre Schaltung baut. Der Vorteil liegt in der Mobilität. Sie können es nach Fertigstellung zum Lehrertisch bringen, wo dieser es begutachten und bei Bedarf an ein Oszilloskop anschließen kann. Wird man in einer Unterrichtsstunde nicht fertig lässt sich das Schaltbrett auch bequem in einem Schrank verstauen und zu einem späteren Zeitpunkt fortsetzten. Die Zeit für einen großen Auf-und Abbau wird gespart.

Einsatz in Vertretungsstunden

Es kommt vor, dass man als Physiklehrer eine Stunde vertreten muss, ohne vorher Zeit für Vorbereitungen zu haben. Man weiß oft nicht, auf welchen Kenntnisstand die Schüler sind und kennt nur grob das Themengebiet, das in dieser Klasse gerade behandelt wird. Dieser Versuch ist durch seinen vergleichsweise einfachen und vor allem schnellen Aufbau, welcher keine großen Vorbereitungen verlangt, bestens dafür geeignet, ihn in der Vertretungsstunde zum Thema zu machen. Der Umfang einer Schulstunde kann bequem mit diesen Experiment gefüllt werden. Sollte man eine Lehrkraft mehr als eine Stunde vertreten, kann der Umfang auch passend ausgeweitet werden.

Zur Veranschaulichung des Zusammenhangs zwischen Mechanik und Elektrizitätslehre

Da mechanische Schwingungen bereits behandelt wurden, kann man diese mit elektromagnetischen Schwingungen vergleichen.

Schwingkreis	Federpendel mit Massestück
Der Kondensator wird geladen [Auslenkung maximal]	Die Feder wird gespannt [Ladung maximal]
Kondensator wird mit Spule verbunden	Massestück wird losgelassen
Ladung nimmt ab, Stromstärke nimmt zu	Auslenkung nimmt ab, Geschwindigkeit nimmt zu
Kondensator ist entladen [Ladung ist 0], Stromstärke ist maximal	Ruhelage [Auslenkung ist 0], Geschwindigkeit ist maximal
Kondensator wird entgegengesetzt geladen [Ladung nimmt zu]	Das Massestück bewegt sich weiter [Auslenkung nimmt zu]
Kondensatorspannung ist maximal, Stromstärke ist 0	Am Umkehrpunkt ist die Auslenkung maximal, Geschwindigkeit ist 0

Dies lässt sich fortführen, indem man die Energien gegenüberstellt.

Schwingkreis	Federpendel mit Massestück
elektr. Feldenergie am Kondensator $E_{el}={\frac {1}{2}}{\frac {1}{C}}Q^{2}$	Potenz. Energie der Feder $E_{pot}={\frac {1}{2}}Ds^{2}$
magn. Feldenergie der Spule $E_{mag}={\frac {1}{2}}LI^{2}$	Kin. Energie des Massestücks $E_{kin}={\frac {1}{2}}mv^{2}$

Stellt man hier eine Differentialgleichung auf und löst sie ergibt sich folgender Zusammenhang:

Schwingkreis	Federpendel mit Massestück
$L{\ddot {Q}}+{\frac {1}{C}}Q=0$	$m{\ddot {s}}+Ds=0$
$\omega _{0}={\sqrt {\frac {1}{LC}}}$	$\omega _{0}={\sqrt {\frac {D}{m}}}$

Diese Gegenüberstellung soll bezwecken, dass die Schüler erkennen, dass es bei physikalischen Phänomenen Gemeinsamkeiten gibt, obwohl sie unterschiedlichen Teilbereichen angehören. So soll das Verständnis beim Schüler gestärkt werden, dass die einzelnen Teilbereiche der Physik nicht abgeschottet voneinander existieren und eigenen Gesetzten folgen, sondern eine Ganzheit herrscht.

Versuchsanleitung

Aufbau

Material:

• ein oder mehrere Kondensator(en)
• ein oder mehrere Spule(n)
• Oszilloskop oder ein anderes Messgerät, welches den Spannungsverlauf festhalten kann (z.B. Cassy)
• Computer/Laptop falls mit Cassy gearbeitet wird
• 3-Weg-Schalter
• Netzgerät für Gleichspannungen
• Verbindungskabel

Für diesen Versuch werden die Bauteile wie im Schaltplan gezeigt aufgebaut. Die Spannung ließt man am besten über den Kondensator ab. Bei den Größen des Kondensators und der Spule muss darauf geachtet werden, dass die zu erwartende Frequenz nach der Thomson´schen Schwingungsgleichung durch das Messgerät (Oszilloskop/Cassy) noch angezeigt werden kann. Es empfiehlt sich Größen von 10-100μF und 500H zu nehmen. Es sei zu beachten, dass die Spannung des Netzgeräts die zugelassene Höchstgrenze des Kondensators nicht überschreitet.

Wenn vorhanden bietet es sich an, die Bauteile auf ein Steckbrett aufzubauen, da es bei Demonstrationszwecken zur besseren Übersicht verhilft. Generell sei darauf zu achten, dass die Schüler den kompletten Aufbau begutachten können, damit bei ihnen keine Unsicherheit dahingehend aufkommt.

Durchführung

Der Schalter wird so eingestellt, dass das Netzgerät und der Kondensator einen geschlossenen Stromkreis bilden. Daraufhin wird das Netztgerät eingeschaltet, was ein Aufladen des Kondensators zur Folge hat. Nach kurzer Zeit ist dieser voll geladen und man betätigt den Schalter. Nun bilden Kondensator und Spule einen abgeschlossenen Stromkreis, ohne Energiezufuhr vom Netzgerät zu erhalten. Dies hat zur Folge, dass sich der Kondensator entlädt. Aufgrund der Selbstinduktion der Spule lädt er sich jedoch wieder auf. Dies wiederholt sich, bis auf Grund von ohmschen Widerständen keine Energie mehr vorhanden ist, um den Kondensator aufzuladen. Man kann nun den Schalter wieder auf die Ausgangsposition stellen und das Ganze wiederholen. Arbeitet man mit Cassy kann man einen Durchlauf bequem aufzeichnen lassen und sogar mit einem Beamer für alle Schüler live sichtbar machen. Aber auch mit einen Oszilloskop kann man den Kurvenverlauf zeigen, jedoch ist eine Auswertung durch Fehlen von Messwerten nicht möglich bzw. sehr umständlich abzulesen.

Ergebnisse

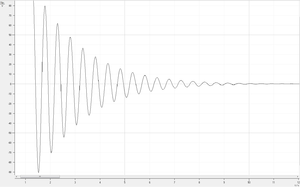
Die Aufzeichnung mit Cassy und Bauteilen der Werte 10μF und 500H ergeben die im Bild aufgezeigte Messkurve. Hält man die Maxima in ein Diagramm fest, erhält man Folgendes:

Zeit in s	Spannung in V	Zeit seit letztem Punkt
1,785	79,5	0
2,295	61,8	0,510
2,800	47,6	0,505
3,310	36,5	0,510
3,815	27,6	0,505
4,315	20,8	0,500
4,825	15,6	0,510
5,315	11,8	0,490
5,810	8,8	0,495
6,295	6,6	0,485
6,785	5,0	0,490

Auswertung

Da sich im Kurvenverlauf schon ein exponentieller Abfall der Spannung vermuten lässt, kann man diesen überprüfen, indem man den Logarithmus des Quotienten aufeinanderfolgender Maxima bildet. Bezeichnet man die Messpunkte mit $P_{n}$ und ergeben sich mit $ln(P_{n}/P_{n+1})$ folgende Werte:

n	$ln(P_{n}/P_{n+1})$
1	0,25
2	0,26
3	0,27
4	0,28
5	0,28
6	0,29
7	0,28
8	0,29
9	0,29
10	0,28

Die Werte schwanken leicht, was auf Unsicherheiten des Experiments zurückzuführen ist. Dennoch ist zu erkennen, dass es sich tatsächlich um einen exponentiellen Abfall handelt. Eine weitere Möglichkeit der Auswertung besteht darin, die Werte der Bauteile zu variieren und so die Abhängigkeit der Frequenz von diesen Werten zu untersuchen. Wurde die Thomsonsche Schwingungsgleichung bereits im vorangegangenen Unterricht eingeführt, lässt sich so ihre Gültigkeit nachweisen und bei Bedarf auf Messunsicherheiten eingegangen werden.

Sicherheitshinweise

Da bei diesen Versuch mit Strom gearbeitet wird gelten die allgemeinen Richtlinien zur Sicherheit im Unterricht im Umgang mit Strom und Spannungen. Weiterhin sollte man nicht vergessen, dass nach abschalten des Netzgeräts der Kondensator weiterhin geladen sein kann.