Ein-Ausschaltvorgang einer Spule

Ein-Ausschaltvorgang einer Spule
Reihenschaltung von Widerstand und Spule Bestimmung der Induktivität durch Halbwertszeitmessung
Kurzbeschreibung
Induktivitätsbestimmung einer Spule durch Halbwertszeitmessung
Kategorien
Elektrizitätslehre
Einordnung in den Lehrplan
Geeignet für:	Sek. II
Basiskonzept:	Wechselwirkung
Sonstiges
Durchführungsform	Schülergruppenexperiment
Anzahl Experimente in dieser Unterkategorie	2
Anspruch des Aufbaus	mittel
Informationen
Name:	Oliver Suckow
Kontakt:	${\text{olib89}}$@${\text{gmail.com}}$
Uni:	Humboldt-Universität zu Berlin
Betreuer*in:	Dr. Franz Boczianowski

Im folgenden soll der Einschalt- bzw. Ausschaltvorgang einer Spule genutzt werden, um quantitativ eine Herleitung für den Zusammenhang von Halbwertzeit und Widerstand/Induktivität herzuleiten. Anschließend lässt sich die Induktivität durch messen der Halbwertzeit bestimmen, welches ebenfalls in diesem Artikel behandelt wird.

Didaktischer Teil

Der Umgang mit dem Computer bekommt in der heutigen Zeit eine immer größere Bedeutung. Wo früher im Physikunterricht der Computer und die Datenauswertung mit diesen eine untergeordnete Rolle spielt, könnte heutzutage die computerorientierte Auswertung eine größere Bedeutung beigemessen werden. In vielen Berufen sind umfangreiche EDV-Kenntnisse von Nöten, sodass diese auch im Unterricht als Kompetenz gefördert werden sollten. Der hier beschriebene Versuch, soll einen Beitrag dazu leisten, physikalische Messergebnisse mittels Computer (Excel) auszuwerten.

Einbettung im Unterricht

Bevor die Versuche durchgeführt werden, sollte im Unterricht der propotionale Zusammenhang Zwischen Halbwertzeit und Induktivität/Widerstand gemäß: $T_{\frac {1}{2}}=ln(2)\cdot {\frac {L}{R}}$ hergeleitet werden. Die Versuche dienen zur Bestätigung der aus der Theorie gewonnen Gleichung (Eine Herleitung ist der Quelle: http://www.ld-didactic.de/literatur/hb/d/p3/p3621_d.pdf zu entnehmen). Der umgekehrte Weg, also die experimentelle Bestimmung der propotionalen Zusammenhang ohne Vorwissen, könnte Probleme bei der Auswertung machen. So kommen die SuS wohlmöglich nicht auf den Vorfaktor ln(2), sodass Sie die Gleichung nicht vollends experimentell bestimmen können. Daher ist es wichtig, dass die SuS den physikalischen Zusammenhang in der Theorie im Vorfeld behandelt haben und mit Hilfe der hier dargestellten Experimente verifizieren können.

Computerunterstützte Auswertung

Bei der Auswertung der Ergebnisse müssen die SuS zunächst die Halbwertzeit bestimmen. Dies können sie auf 2. verschiedene Arten machen. Zum einen können die SuS mit Hilfe der Cassy-Software die Halbwertzeit direkt aus dem Diagramm ablesen. Diese Methode eignet sich besonders gut für eine schelle Auswertung. Das Problem ist aber, dass diese Methode mit einer großen Messunsicherheit verbunden ist. Die 2. Möglichkeit wäre es, mit Hilfe der Cassy-Software sich die Ergebnisse als Excel-Kompatibles Format ausgeben zu lassen. So lassen sich durch sortieren der einzelnen Spalten nach Größe die maximale bzw. minmale Spannung bestimmen. Aus der Differenz ${\frac {U_{max}-U_{min}}{2}}$ lässt sich die Hälfte der maximalen Spannung bestimmen. Die zugehörigen Zeiten werden ebenfalls notiert. Anschließend können die SuS die Spannung der größe nach sortieren lassen um den mittleren Spannungswert und die dazugehörige Zeit $T_{Mitte}$ zu bestimmen. Aus der Zeitdiffernenz $T_{1/2}=T_{max}-T_{Mitte}$ lässt sich nun die Halbwertzeit berechnen. Das vorgehen wird für jeden Paar Induktivität/Widerstand wiederholt. Die erhaltene Messwerte können in eine Excel-Tabelle eingefügt werden. Mit Hilfe der Plot-Funktion von linearen Funktion lässt sich die Steigung (ln(2)) durch das Programm berechnen.

Der Umgang mit Daten und die computerunterstützte Auswertung von Messwerten kann besonders gut, bei der Halbwertzeit Bestimmung geschult werden, da mehrere Schritt nötig sind um diese zu bestimmen. Auch macht die schnelle Datenanalyse durch sortieren der Spalten und direkte Berechnung der Spannungsdiffernzen bzw. der Halbwertzeit, das Verfahren sehr effektiv (zeitlicher Aspekt).

Die so erworbene Kompetenz ist nicht nur Fachspezifisch und kann daher in anderen Unterrichtsfächer angewandt bzw. im Leben eine Verwendung finden. Somit genügend sie dem Prinzip der Gegenwartsbedeutung und Zukunftsbedeutung nach Klafki und trägt zusätzlich zur computerorientierten Kompetenzbildung bei.

Versuchsanleitung

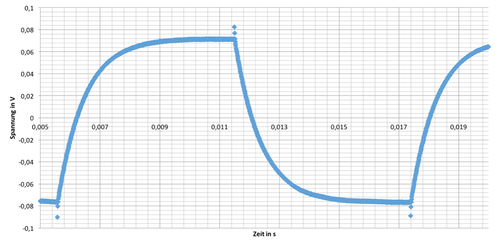
Wird ein Stromkreis, indem eine Spule enthalten ist, abgeschaltet so fällt die Spannung auf Grund der Selbstinduktion kontinuierlich ab (siehe Abbildung "Spannungsverlauf in Abhängigkeit der Zeit"). Mit Hilfe des Cassys lässt sich die Spannung in Abhängigkeit der Zeit messen. Durch Messen der Halbwertzeit (Zeitdifferenz bis zum Abfall der Spannung auf die Hälfte) lässt sich die Induktivität der Spule gemäße $L=T_{\frac {1}{2}}\cdot {\frac {R}{ln(2)}}$ bestimmen. Im folgenden soll zunächst der physikalische Zusammenhang zwischen Induktivität, elektrischen Widerstand und Halbwertzeit experimentell bestimmt werden. Anschließend wird dieser Zusammenhang genutzt, um die Induktivität verschiedener Spulen zu bestimmen.

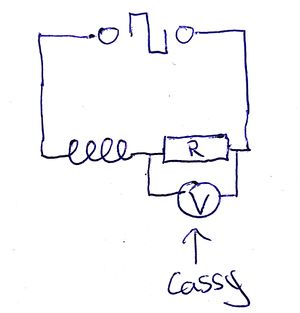
Aufbau

Für den Versuch wird zunächst eine Spule (austauschbar) mit einem Widerstand (austauschbar) in Reihe geschalten. Als Spannungsquelle dient eine Wechselspannung, die mit Hilfe eines Frequenzgenerators in Reihe eine Rechteckspannung liefert. Parallel zum Widerstand wird mit Hilfe von Cassy die Spannung in Abhängigkeit der Zeit gemessen (siehe Schaltplan).

Schaltplan

Durchführung

Vorbereitung

Zunächst muss am Computer die Software für Cassy gestartet werden( alternative zu Cassy lässt sich die Spannung in Abhängigkeit der Zeit auch mit Hilfe eines Oszillators bestimmen). Die Spannungsquelle (Wechselspannung 6v) wird eingeschaltet und der Frequenzgenerator so eingestellt, dass eine Periode mit Hilfe von Cassy am PC dargestellt werden kann. Da durch Selbstinduktion eine Gegenspannung induziert wird, sollte die Frequenz ausreichend lang gewählt werden.

Nachweis des Physikalischen Zusammenhangs $T_{\frac {1}{2}}=ln(2)\cdot {\frac {L}{R}}$

Für verschiedene Widerstände und gleicher Spule wird durch das Cassy der Verlauf der Spannung in Abhängigkeit der Zeit gemessen. Auch lassen sich zwei Spulen parallel schalten, um weitere Messwerte zu erhalten (Reihen-Parallelschaltung von Spulen beachten). Aus den Graphen wird zu jeder Induktivität/Widerstand-Paar die Halbwertzeit des Spannungsabfalls bestimmt. Die Wertepaare lassen sich abschließend in einem Koordinatensystem abtagen.

Induktivitätsbestimmung

Ist der physikalische Zusammenhang $L=T_{\frac {1}{2}}\cdot {\frac {R}{ln(2)}}$ bekannt, so kann mit Hilfe der Halbwertzeitbestimmung die Induktivität berechnet werden. Das vorgehen ist analog zu Abschnitt 2.2.2 .

Ergebnisse und Auswertung

Nachweis des Physikalischen Zusammenhangs $T_{\frac {1}{2}}=ln(2)\cdot {\frac {L}{R}}$

Spannungsverlauf in Abhängigkeit der Zeit

Im folgender Tabelle sind die Messwerte für die Halbwertzeit bei verschiedenen Widerständen dargestellt. Zusätzlich wurde die gleiche Spule einmal in Reihe und ein mal Parallel zu einer Spule mit selber Induktivität geschalten:

Gesamtwiderstand in Ohm	Halbwertzeit in s	Induktivität in H	L/R in H/Ohm
47	0,00074	0,05	0,001
57	0,00063	0,05	0,0008
69	0,00048	0,05	0,00072
107	0,00031	0,05	0,00046729
92	0,0064	0,1 (Reihe)	0,001
24,5	0,0007	0,025 (Parallel)	0,001

Die Messunsicherheit der Halbwertzeit wird durch Abschätzen zu $\pm 0,00005$ angegeben. Die Messunsicherheiten des Widerstands ($\pm 5\%$) bzw. der Induktivität ($\pm 4\%$) sind der Herstellerangabe entnommen.

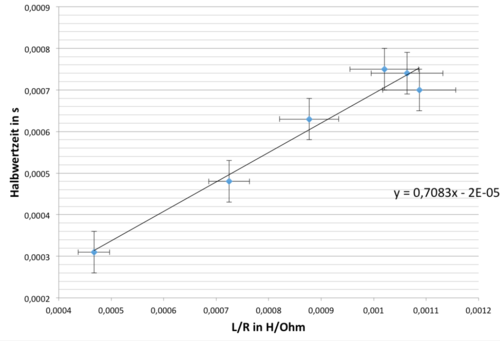
Trägt man die Werte in ein Koordinatensystem ein, so erhalten wir folgenden Zusammenhang:

Ergebnisse

Alle Wertepaare liegen auf einer Geraden, sodass gilt $T_{\frac {1}{2}}\sim {\frac {L}{R}}$. Die Steigung beträgt 0,7 was rund ln(2) entspricht. Somit folgt der Zusammenhang:

$T_{\frac {1}{2}}=ln(2)\cdot {\frac {L}{R}}$

Induktivitätsbestimmung

Mit Hilfe der Gleichung $L=T_{\frac {1}{2}}\cdot {\frac {R}{ln(2)}}$ lässt sich die Induktivität einer Spule bestimmen. Die Messunsicherheit des Widerstand ist dem Hersteller zu entnehmen ($\pm 5\%$) und die Messunsicherheit der Halbwertzeit wird analog zu Abschnitt 2.2.2. mit 0,00005 s abgeschätzt. Durch Fehlerfortpflanzung ergibt sich die Messunsicherheit der Induktivität, wie der folgenden Tabelle zu entnehmen ist:

Gesamtwiderstand in Ohm	Halbwertzeit in s	berechnete Induktivität in H	Messunsicherheit in H	Referenzwert
47	0,00074	0,050	0,004	0,05
57	0,00063	0,052	0,005	0,05
69	0,00048	0,048	0,006	0,05
107	0,00031	0,048	0,008	0,05
92	0,0007	0,093	0,008	0,1
24,5	0,00075	0,027	0,002	0,025

Die Messwerte stimmen somit im Rahmen der Messunsicherheiten mit den Referenzwerten der Hersteller überein.

Literatur

• LD Handblätter Physik: Messung des Stromverlaufes in einer Spule beim Ein- und Ausschalten von Gleichstrom; http://www.ld-didactic.de/literatur/hb/d/p3/p3621_d.pdf [30.09.2015]