Druckwasserrakete mit dem Smartphone
| Druckwasserrakete mit dem Smartphone | |
 Rakete vor dem Start | |
| Kurzbeschreibung | |
|---|---|
| Druckwasserrakete mit Smartphone als Messgerät | |
| Kategorien | |
| Digitales Messen, Mechanik | |
| Einordnung in den Lehrplan | |
| Basiskonzept: | Energie, Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Demoexperiment |
| Anzahl Experimente in dieser Unterkategorie | 1 |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Johannes Mauch, Maren Söder, Stephen Mayer |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Franz Boczianowski |
Im Vergleich zu Arduino-Boards haben Smartphones einen höheren Lebensweltbezug für Schüler:innen und zudem haben sie bei der Bedienung weniger Probleme. Deshalb wurde das Arduino-Board aus dem ersten Versuch Druckwasserrakete mit Arduino hier mit einem Smartphone ersetzt. Die Motivation für den Versuch an sich ist jedoch dieselbe wie im ersten Versuch.
Inhaltsverzeichnis
Versuchsanleitung
Aufbau
Die Rakete
Es wurde dieselbe Rakete wie im ersten Versuch genutzt, allerdings gab es ein paar Abwandlungen. Der Laderaum wurde vergrößert, da das zu nutzende Smartphone zu groß für den alten Laderaum war. Außerdem wurde auf den Fallschirm verzichtet, da die Spitze der Rakete sich nach Erreichen der Maximalhöhe nicht vom neuen Laderaum löst.
Die Messeinrichtung
Der Versuch kann ganz einfach mit dem bereits vorgefertigten Experiment 'Aufzug' in 'phyphox' durchgeführt werden. Es ist nur darauf zu achten, ein Smartphone zu nutzen, das sowohl die Beschleunigung als auch den Luftdruck messen kann.
Durchführung
Es wurden insgesamt acht Flüge durchgeführt mit Füllständen zwischen 100 und 800 ml. Der Druck in der Rakete wurde jeweils auf ungefähr 5 bar erhöht. Mithilfe des Fernzugriffes in 'phyphox' kann dann die Messung in der App und danach die Rakete gestartet werden.
Ergebnisse
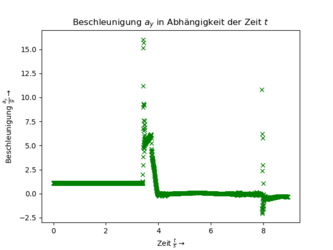
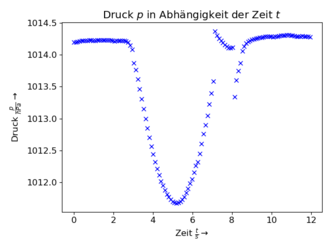
Exemplarisch sind hier die Messdaten der Beschleunigung in y-Richtung und des Drucks für den Füllstand 500 ml dargestellt. Mithilfe der barometrischen Höhenformel kann aus dem Druck die Flughöhe bestimmt werden. Das erneute Absinken des Druckes am Ende, das auf die Öffnung des Laderaums zurückgeht, wurde nicht in Höhenmeter umgerechnet.I
|
|
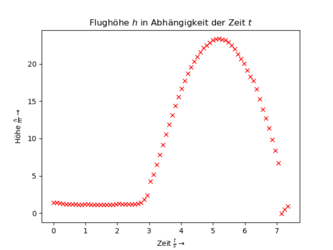
|
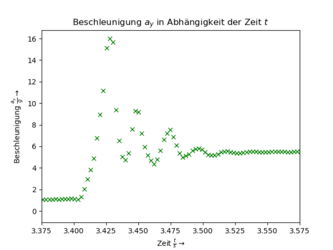
In der ersten Zehntelsekunde ist eine starke Oszillation der Beschleunigung im folgenden Diagramm zu erkennen.
Auswertung
Exemplarflug mit 500 ml Füllstand
Mithilfe des Beschleunigungsdiagramms lässt sich der Flug der Rakete in drei Phasen einteilen. In der ersten Phase vor dem Start der Rakete (bis ungefähr 3,5 Sekunden) erfährt das Smartphone nur die Erdbeschleunigung. Anschließend wird das Smartphone durch das austretende Wasser mit ungefähr 5,5 g beschleunigt. Nach ungefähr 4 Sekunden ist das Wasser verbraucht und die Beschleunigung fällt auf 0 g, da der Sensor und dessen Gehäuse nun beide die Erdbeschleunigung erfahren. Nach ungefähr 8 Sekunden kommt die Rakete wieder auf dem Boden auf und anschließend beträgt die Beschleunigung wieder 0 g, allerdings liegt dies im Vergleich zur ersten Phase daran, dass das Smartphone nun gedreht liegt und die Erdbeschleunigung nicht mehr in der y-Komponente gemessen wird.
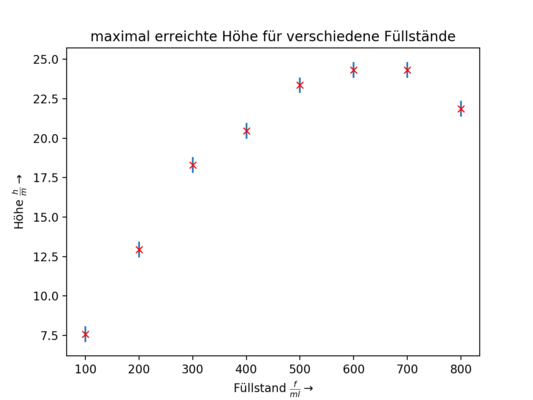
Variation der Füllstände
Im folgenden Diagramm sind die jeweils maximal erreichten Höhen inklusive Unsicherheiten für die verschiedenen Füllstände zu sehen.