Drehmoment
| Drehmoment | |
 Teil des Aufbaus des Experimentes (Kreisscheibe, Lichtschranke und System zur Beschleunigung der Kreisscheibe) | |
| Kurzbeschreibung | |
|---|---|
| Verifizierung der Aussage, dass ein konstantes Drehmoment eine gleichmäßig beschleunigte Bewegung erzeugt. | |
| Kategorien | |
| Mechanik | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. II |
| Basiskonzept: | Wechselwirkung |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment, Schülergruppenexperiment |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Julia Irmisch |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Nico Westphal |
Bei diesem Experiment wird der proportionale Zusammenhang zwischen dem Betrag der Winkelbeschleunigung und dem Betrag des Drehmoments untersucht, der aus der Formel folgt . Dabei wird eine Kreisscheibe durch ein konstantes Drehmoment beschleunigt und diese Bewegung mit Hilfe einer Lichtschranke und einem dazugehörigen Zeitmesser untersucht. Die Ergebnisse des Experimentes lassen sich gut durch die Schüler interpretieren.
Da unter Umständen nur ein Experiment dieser Art einer Schule zur Verfügung steht, aber mehrere Messungen benötigt werden und damit die Durchführung und Auswertung zeitaufwendig sind, empfiehlt es sich, parallel andere Aufgaben für die Schüler bereit zu halten, die nicht gerade an dem Experiment arbeiten können.
Die Idee zu diesem Experiment ist einem Physik-Schulbuch [1] entnommen.
Inhaltsverzeichnis
Didaktischer Teil
Es wird von der aufgestellten Gleichung ausgegangen, die man aus den bekannten Gleichungen der Translationsbewegung durch Analogieüberlegungen herleiten kann, wobei von (Trägheitsmoment) wenigstens bekannt sein sollte, dass es das Analogon zu (Masse) und konstant ist. Den Lernenden muss an dieser Stelle verdeutlicht werden, dass die Gültigkeit dieser Analogieüberlegung erst bewiesen werden muss. Um die Situation zu vereinfachen, kann man sich mit den Lernenden darauf einigen, dass es genügt den vereinfachten Zusammenhang bzw. zu zeigen. Der Beweis kann dann mit Hilfe dieses Experimentes vorgenommen werden.
Die Schüler können leicht erkennen, dass das Drehmoment die Größe ist, die man vorgeben und von Versuch zu Versuch variieren kann und auch, dass man die Winkelbeschleunigung nicht direkt messen kann. Bei dem unten erläuterten Aufbau ist es möglich die Winkelgeschwindigkeit zu messen. Doch da dies möglicherweise nicht bei allen Varianten des Versuchsaufbaus möglich ist und weil es auch didaktisch sinnvoller ist, sollte man den Schülerinnen und Schülern diese Möglichkeit nicht geben. Die Lernenden können erkennen, dass sie während einer Drehung in regelmäßigen Abständen die Zeiten messen lassen können, in denen eine durch das Drehmoment beschleunigte Kreisscheibe einen bestimmten Winkel überstreicht. Hier ist die Tatsache, dass abhängig von der Dauer der Beschleunigung, also zeitabhängig ist, ein wichtige Erkenntnis.
Es müssen mehrere Versuche durchgeführt werden, für die jeweils das Drehmoment konstant ist.
Die Winkelgeschwindigkeit nimmt also linear zu. Also kann man nun Folgendes schlussfolgern:
Der erwartete Graf der Messergebnisse ist also hyperbelförmig.
Didaktisch sinnvoller ist die beschriebene Variante deswegen, weil dadurch der Erkenntnisprozess vollendet wird. Lassen sich die Lernenden sofort die Winkelgeschwindigkeit anzeigen, denken sie nicht mehr über den Zusammenhang nach, zwischen dem was eigentlich gemessen wird und den angegebenen Werten. Denn das System misst ja weiterhin nur die eben beschriebenen Zeiten. Zudem lassen sich dann die Ursachen von Unregelmäßigkeiten bei Messungen leichter ermitteln und nachvollziehen. Außerdem lohnt sich gerade bei diesem Experiment auf diese Hintergrundüberlegungen zu bestehen, da die Ergebnisse sehr genau sind und stets den Erwartungen entsprechen (bitte dazu "allgemeine Hinweise“ beachten!). Der beschriebene hyperbelförmige Graf ist tatsächlich zu sehen und die aus den Messwerten ermittelten Winkelgeschwindigkeiten ergeben tatsächlich offensichtlich eine Gerade und nicht nur, wie oft bei anderen Experimenten, „so ungefähr“. Ein weiterer Vorteil des Experimentes ist, dass man mit den Schülerinnen und Schülern gut über Messunsicherheiten sprechen kann. Denn insbesondere bei der Verwendung leichter Massestücke hat die Reibung einen Einfluss, welcher bei schweren Massestücken nicht mehr sichtbar und vernachlässigbar klein ist (siehe "Allgemeine Hinweise").
Voraussichtlich wird es kaum möglich sein, in einer Schule mehrere solcher Experimente aufzubauen. Mehrere Messungen dieser Art durchzuführen und auszuwerten, ist sehr zeitaufwendig. Eine gute Möglichkeit wäre, die Schülerinnen und Schüler in Gruppen einzuteilen, die nacheinander das Experiment durchführen und aus ihren eigenen Messwerten die Winkelbeschleunigung zu den jeweiligen Drehmomenten bestimmen. Am Schluss kann man die Ergebnisse der Klasse sammeln und die gesuchte Proportionalität nachweisen.
Versuchsanleitung
Aufbau
Für dieses Experiment wird benötigt:
- verschiedene Massestücke (z.B. 10g, 20g, 50g)
- ein Drehsystem (reibungsfrei gelagerte Kreisscheibe, feste Rolle, langer Faden)
- Lichtschranke mit Zeitmesser
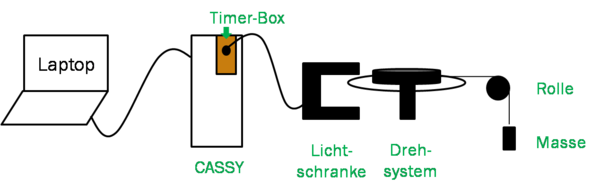
Beim Aufbau des hier dargestellten Experimentes wurde das "Computer Assisted Science System" (kurz: CASSY[2]) der Firma Leybold verwendet, um die von der Lichtschranke registrierten Zeiten zu messen und auszuwerten. Die Durchführung lässt sich jedoch gut auf andere Messsysteme übertragen, die in der Schule womöglich eher zu finden sind als das CASSY. Für die Verwendung mit CASSY wird die Software CASSY Lab, das Gerät Sensor-CASSY (in Abb. 1 kurz mit CASSY bezeichnet) und zusätzlich die sogenannte Timer-Box benötigt. Der Aufbau erfolgt wie in Abb .1 dargestellt. Dabei wird der Faden um den Aufsatz der Kreisscheibe gewickelt, über die feste Rolle geführt und mit einem Massestück beschwert. Dabei ist es wichtig, dass der Faden zwischen Kreisscheibe und Rolle wirklich waagerecht ist, zur einfacheren Bestimmung des Drehmoments während des Experimentierens.
Es ist empfehlenswert bei der Wickelung des Fadens einen möglichst kleinen Radius zu wählen, da sich die Scheibe andernfalls sehr schnell dreht. Ein kleinerer Radius ermöglicht mehr Messwerte und unter Umständen genauere Messwerte. Am besten sollte man dies, vor dem Experimentieren mit den Schülern, ausprobieren.
Wenn die Kreisscheibe des Drehsystems durchsichtig ist, wie in der Skizze dargestellt, kann man das System auf einem Overhead-Projektor aufbauen. Schließt man zusätzlich den PC an einen Beamer an, können die Schüler das Experiment von ihren Sitzplätzen aus beobachten. Das kann zum Beispiel aussehen wie Abb. 2 dargestellt:
Durchführung
Mit Hilfe von CASSY gibt es zwei Möglichkeiten das Experiment durchzuführen, je nachdem welche Kreisscheibe zu Verfügung steht. Hier werden beide Varianten erklärt. Für die Schüler genügt es, eine der beiden Varianten zu verwenden.
Auf einer der möglichen Kreisscheiben sind 360 Markierungen im Abstand von je einem Grad angebracht. Mit der Einstellung "Periodendauer" im CASSY-Lab misst das CASSY die Zeit von einer Markierung zur nächsten in eingestellten Zeitintervallen (z.B.100ms). Das bedeutet zum Beispiel, dass CASSY alle 100ms einen neuen Messwert aufnimmt.
Auf einer anderen Kreisscheibe ist eine 10° breite dunkle Markierung angebracht, deren Durchlaufzeit durch die Lichtschranke das CASSY in einem zuvor festgelegten Zeitraum bei der Einstellung "Dunkelzeit" misst.
Für die Messungen muss sich die Kreisscheibe drehen. Dazu wird die Masse am Faden frei hängen gelassen. Die (konstante) Gewichtskraft des Massestücks bewirkt ein konstantes Drehmoment. Kurz nach Beginn der Drehung kann die Messung gestartet werden. Bevor das Massestück den Boden berührt, wird die Messung gestoppt.
Ergebnisse
eine Beispielmessung
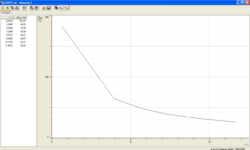
Die Messungen mit 10g ergaben die beiden Diagramme Abb. 3 und Abb. 4. Die Abzisse gibt den Messzeitpunkt wieder (), während an der Ordinate die Messergebnisse () abgetragen werden. Abb. 3 stellt die Messvariante "Periodendauer" dar. Aus diesem Bild wird auch ersichtlich, warum die Beobachtung der Drehscheibe während des Experimentes nötig ist. Die Zacken in der Kurve würden bedeuten, dass die Drehung zwischenzeitlich kurzzeitig langsamer werden würde, dass ist aber nicht beobachtbar. Stattdessen kann man diese Zacken auf Kratzer oder auch Staub auf der Drehscheibe zurückführen.
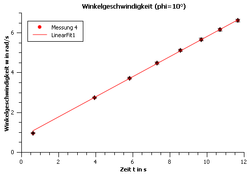
Auf dem Bild der Abb. 4 sind die Messergebnisse der Messvariante "Dunkelzeit" dargestellt. Da die 10° breite Markierung nur einmal auf der Kreisscheibe angebracht ist, gibt es deutlich weniger Messwerte. Dafür gibt es aber auch keine deutlich sichtbaren Unregelmäßigkeiten. Dazu sei angemerkt, dass das Programm an dieser Stelle die Messwerte mit Linien verbunden hat.
Es sind also folgende Parameter bekannt bzw. ablesbar: , , . Damit ist in Abhängigkeit von der Zeit für beide Varianten bestimmbar. Bei der Berechnung der Ergebnisse müssen natürlich auch die Messunsicherheiten und ihre Fortpflanzung berücksichtigt werden. Dies wird ausführlich im Abschnitt "Messunsicherheiten" erläutert.
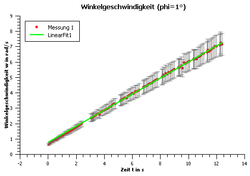
Die errechneten Werte für können dann mit einem Programm (hier: QTI-Plot) grafisch dargestellt werden. Das Programm verfügt zudem über die Möglichkeit, Messwerte zu fitten. In den unteren Bildern sind die dabei entstandenen Grafen dargestellt. Gemäß der Gleichung , entspricht der Anstieg des gefitteten Grafens der Winkelbeschleunigung, die der beobachteten Drehbewegung zugeordnet ist.
Diese Messungen können nun mit anderen Massestücken wiederholt werden.
Auswertung
Dieses Experiment wurde mit unterschiedlichen Massen und den beiden beschriebenen Methoden durchgeführt. Das führte zu folgenden Ergebnissen.
| Masse | Methode "Dunkelzeit" | Methode "Periodendauer" |
|---|---|---|
| 1g | ||
| 2g | ||
| 10g | ||
| 20g | ||
| 50g |
(Die Messungen, die nicht durchgeführt wurden, sind mit "" gekennzeichnet.)
Werden mehrere Messungen zu einem Massestück durchgeführt, kann der Mittelwert berechnet werden und mit Hilfe der Standardabweichung und der systematischen Messunsicherheit eine Gesamtunsicherheit berechnet werden. Sinnvoll ist dies jedoch nur bei mindestens sechs Messwerten.
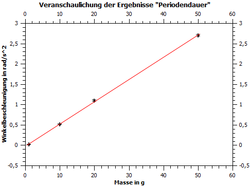
In der Grafik (Abb. 7) sind die Ergebnisse zu den Messungen der Methode "Periodendauer" veranschaulicht. Es ist klar zu sehen, dass hier ein konstanter Anstieg vorliegt. Gleiches gilt für die Veranschaulichung der Methode "Dunkelzeit".
Damit ist zumindest für einen festen Radius gezeigt: .
Messunsicherheiten
Es stellt sich heraus, dass es eine Unsicherheit gibt, die die größte Rolle spielt. Bei der Betrachtung der Markierungen fiel auf, dass die Ränder Unregelmäßigkeiten aufweisen. Die Unsicherheit kann mit abgeschätzt werden. Die Gesamtunsicherheit wird mit der Formel der Gaußschen Fehlerfortpflanzung bestimmt, d.h. in diesem Fall:
Eine weitere Unsicherheit entsteht bei diesem Experiment durch die Rundung der Messwerte durch das CASSY. Allerdings sind die Messwerte auf genau angegeben und die Unsicherheit ist damit im Vergleich zu der obigen Unsicherheit sehr gering. Dabei ist natürlich zu beachten, dass andere Messgeräte auch andere Unsicherheiten besitzen und dass die Fehlerfortpflanzungsrechnung entsprechend angepasst werden muss. Auch die Breite des Lasers der Lichtschranke spielt sicherlich eine gewisse Rolle. Dazu gibt es aber keine Angaben in dem dazugehörigen Handbuch, außerdem kann man annehmen, dass dies bei der Genauigkeit der Messwerte berücksichtigt wurde. Auch das nicht gleichmäßige Rotieren des Drehtellers ("Eiern") bringt eine Unsicherheit in die Messwerte. Ein Indiz für die Größe des Einflusses in die Messwerte können (zumindest bei der Messvariante "Periodendauer") kleine Schwankungen/Wellen in der Messkurve sein. Diese sind nur schwer abschätzbar, aber auch vernachlässigbar klein. Dazu kommt die Masse des Fadens, die während des Experimentes das Drehmoment und das Trägheitsmoment der Kreisscheibe verändert. Da aber für den Faden ein sehr feines Nähgarn verwendet wurde, ist auch diese Unsicherheit vernachlässigbar.
Ich möchte an dieser Stelle betonen, dass diese Überlegungen zu den Messunsicherheiten nur der Anregung dienen und nicht zwangsläufig auf nachgebaute Experimente übertragbar sind.
Allgemeine Hinweise
Bei der Betrachtung der sich ergebenden Winkelgeschwindigkeiten fällt auf, dass die Werte der Messreihe "Dunkelzeit" niedriger sind, als die der Messreihe "Periodendauer". Die Ursache dafür ist im Aufbau des Experimentes zu finden. Die beiden Kreisscheiben sind unterschiedlich hoch beim Aufsetzen auf dem Standfuß. Für ein gleiches Drehmoment bei gleichen Massestücken, hätte entsprechend die Rolle leicht neu justiert werden müssen. Genauer gesagt, hätte man entweder darauf achten müssen, dass der Faden zwischen Rolle und Kreisscheibe stets waagerecht ist, oder den entsprechenden Winkel in den Rechnungen berücksichtigen müssen. Dies muss bei Nachbauten beachtet werden, sofern das Experiment auf ähnliche Weise wiederholt wird.
Die Massestücke sollten eine Masse von 10g oder mehr haben. Die trotz Kugellager vorhandene geringe Reibung ist besonders bei 1g oder 2g bei geringen Winkelgeschwindigkeiten in den Messwerten sichtbar. So ist die Auswertung des Experimentes für die Schüler zunächst leichter. Es empfiehlt sich aber, mit den Schülern im Anschluss an ihre ersten Gedanken zur Auswertung und zu den Messunsicherheiten eine Messung mit z.B. 1g durchzuführen und auszuwerten, damit sie auch diese Beobachtung in ihre Auswertung mit einbeziehen können.
Literatur
- ↑ Joachim Grehn, Joachim Krause; Metzler Physik, Schroedel Schulbuchverlag, 4. Auflage, Druck A2, Jahr 2008, S.72
- ↑ http://www.ld-didactic.de/index.php?id=cassy-s