Doppler-Effekt (mit Hilfe eines Pendels)
| Doppler-Effekt (mit Hilfe eines Pendels) | |
 Abbildung: Bild des Pendels und des verwendeten Mikrofons | |
| Kurzbeschreibung | |
|---|---|
| Demonstration des Doppler-Effektes mit Hilfe eines Pendels | |
| Kategorien | |
| Mechanik, Akustik, Schallausbreitung | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Sek. I
Jahrgangsstufe 9/10 |
| Basiskonzept: | Akustik (Schallausbreitung) |
| Sonstiges | |
| Durchführungsform | Lehrerdemoexperiment |
| Anspruch des Aufbaus | mittel |
| Informationen | |
| Name: | Christopher Wolf |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
| Betreuer*in: | Franz Boczianowski |
Das Experiment "Doppler-Effekt (mit Hilfe eines Pendels)" (frei nach einem in [1] beschriebenen Aufbau) bietet eine Möglichkeit, den Doppler-Effekt sowohl qualitativ hörbar als auch quantitativ messbar im Unterricht vorzuführen. Damit verdeutlich es ein wichtiges akustisches Phänomen, das einen hohen Alltagsbezug aufweist.
Des Weiteren ist es sehr gut möglich, auf der Basis erhaltener Messergebnisse Aufgaben zu stellen, die die Schüler nach der grundlegenden theoretischen Herleitung mit relativ simpler Hilfestellung selbstständig lösen können sollten.
Im Rahmen dieses Versuches wird nur der akustische Doppler-Effekt behandelt.
Inhaltsverzeichnis
Didaktischer Teil
Ein Abstraktionsschritt der gemacht werden muss ist die Form der Bewegung. Der Doppler-Effekt kann als phänomenologisch bekannt vorausgesetzt werden. Er sollte gut aus Alltagssituationen bekannt sein, vermutlich am besten durch vorbeifahrende Kraftfahrzeuge, die währenddessen Geräusche emittieren. Dafür reichen Motoren- und Abrollgeräusche aus, besser hörbar und bekannter ist der Effekt aber von Sirenen passierender Autos (beispielsweise Feuerwehr- und Polizeiautos oder Krankenwägen.)
Einschätzung des Experimentes
Bei dem hier präsentierten Versuch handelt es sich um ein lehrerzentriertes Realexperiment, das als quantitativer Versuch durchgeführt wird.
[2]
Er bietet sich sowohl als Einstiegsversuch in das Thema, als auch als Versuch zur Vertiefung oder Verständniskontrolle (jedoch muss auch von einer Durchführung als Erarbeitungsversuch nicht abgeraten werden.)[3]
Da es sich um einen Versuch mit physikalischen Apparaturen und Messgeräten handelt, muss der Geräteaufwand mit eingeplant werden (siehe Benötigte Materialien).[3]
Motivation
Der Doppler-Effekt ist ein physikalisches Phänomen, das aus dem Alltag sehr gut bekannt ist. Er lässt sich mit vertretbarem Aufwand anschaulich erklären sowie gut quantifizieren und berechnen, was ihn zu einem geeigneten Unterrichtsgegenstand macht.
Das Verstehen des Doppler-Effektes setzt meist ein umfassendes Verständnis des Konzeptes der Schallwellen und ihrer Ausbreitung voraus und kann deshalb gut zur Vertiefung dieses Themas verwendet werden.
Probleme bei der praktischen Umsetzung
Die geradlinige Bewegung
Oftmals ist es nicht trivial, den Doppler-Effekt sowohl gut hörbar als auch quantitativ messbar im Unterrichtsraum zu demonstrieren.
Das Problem von geradlinigen Bewegungen im Unterrichtsraum ist meist (aufgrund des begrenzten Platzes) dass sie nur sehr kurz sind, oder relativ langsam (da jeweils die zur Verfügung stehende Strecke kurz ist), wodurch der Effekt weniger stark ausgeprägt oder nur kurz auftritt.
Eine geradlinige Bewegung scheint deshalb in den meisten Fällen stark nachteilig zu sein.
Der Lösungsansatz zu dieser Problematik bestand darin, eine geeignete andersförmige Bewegung zu finden.
Die Kreisbewegung
Wird eine Kreisbewegung gewählt besteht der Vorteil darin, dass sie mit mathematischen Modellen gut berechenbar ist und an einigen Bahnpunkten der Bewegung die Geschwindigkeit bestimmt werden kann. Ein weiterer Vorteil besteht darin, dass es oft gut möglich ist, die wirkenden Kräfte zu überschauen und zu berechnen.
Die Pendelbewegung
Schließlich wurde entschieden, die Bewegung eines Pendels zu benutzen. Sie weist viele nutzbare Eigenschaften der Kreisbewegung auf und bietet sich für die Umsetzung des Experimentes an.
Bei der Bewegung eines Pendels
- ist der benötigte Platz (im Vergleich zu anderen möglichen Versuchsaufbauten für diesen Effekt) relativ gering
- kann der Versuchsaufbau gut vorbereitet und getestet werden
- ist die hauptsächlich wirkende Kraft (die Erdanziehung) gut bekannt und im Optimalfall im Unterricht bereits eingeführt
- ist an drei Punkten (an dem Punkt ohne Auslenkung (dem Lotfußpunkt der Aufhängung) und den beiden Punkten maximaler Auslenkung) die Geschwindigkeit der pendelnden Masse leicht zu berechnen.
Einbindung in den Rahmenlehrplan
Das Themengebiet der Akustik findet sich derzeit im aktuellen Rahmenlehrplan (stand 2014) für Berlin nur in der SEK I, in den Jahrgängen 9 und 10 wieder.[4]
Dort gibt es das Pflichtmodul P6: Von der Quelle zum Empfänger, in dem der Doppler-Effekt jedoch kaum einbindbar ist.
Des Weiteren gibt es das Wahlmodul W8: Schwingungen, die man hört, in das der Doppler-Effekt hervorragend einbindbar ist und auch als Themenbeispiel explizit genannt wird (außerdem sind dort auch die für den Doppler-Effekt wichtigen Themen Tonhöhe und Frequenz, Schallausbreitung und Schallwellen angesetzt).
Der theoretische Hintergrund zu dem Versuch ist sehr gut im Physikunterricht vermittelbar.
Laut dem Berliner Rahmenlehrplan kann dieser Unterrichtsinhalt zwar in der Klassenstufe 9/10 behandelt werden, allerdings sollte es weitgehend unproblematisch sein, dieses Thema bereits früher zu behandeln.
Mögliche Schüleraufgaben zu dem Experiment
Zu dem in diesem Artikel geschilderten Versuch lassen sich vielerlei Fragestellungen behandeln, die nach einer Herleitung und ausführlichen Erklärung des Phänomens beantwortbar sind. Außerdem ermöglichen sie es dem Lehrer, das Wissen und das Verständnis der Schüler zu überprüfen oder durch Aufgaben zu fördern.
Mögliche Fragestellungen, die im Zuge des Experiments (in der Vorbereitung oder in der Nachbereitung) gestellt werden könnten sind, unter Anderem:
- Vorhersage der Tonverschiebung durch den Doppler-Effekt bei bekannter Seillänge und Pendelauslenkung
- Bestimmung der maximalen Pendelgeschwindigkeit durch die gemessene (durch den Doppler-Effekt) veränderte Tonhöhe
- Berechnung der Seillänge aus der Veränderung des Tones
Jedoch sind, losgelöst von diesem Aufbau, eine Vielzahl weiterer Aufgaben vorstellbar:
- Schüler sollen, ohne sie zu sehen, die Art einer Bewegung an der Tonänderung durch den Doppler-Effekt identifizieren
- Die Erdbeschleunigung durch den Doppler-Effekt bei einer frei fallenden Schallquelle ermitteln
- Anhand des aufgenommenen Tones die Tonhöhenverschiebung bei einem passierenden Fahrzeug ermitteln und damit dessen Geschwindigkeit errechnen
Versuchsbeschreibung
Aufbau
Alle für den Aufbau benötigten Materialien sollten sich in einer durchschnittlichen Materialsammlung einer Schule befinden, sich aber ansonsten auch größtenteils im Privatbesitz jedes Lehrers finden sollten. Er sollte ferner ungefähr zwischen 15 und 25 Minuten dauern, gesetzt den Fall, dass die benötigte Software bereits installiert ist.
Benötigte Materialien
- Ein Pendel
- Ein Seil der Länge 2,245 Meter
- Eine Masse für das Pendel (Bowlingkugel, Durchmesser etwa 27 cm und Masse 8 kg)
- Eine Aufhängung für das Pendel
- Ein Deckenhaken
- Ein am Seil des Pendels befestigter Karabinerhaken
- Ein Smartphone mit der App "Pro Audio Tone Generator"
- Ein Empfänger
- Ein Mikrofon
- Ein Computer mit der Software Spectrum Lab
- Eine Stoppuhr
Verwendete Software
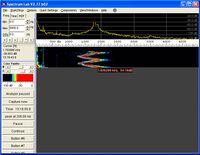
Als Software auf dem Computer wird ein Programm benötigt, dass in der Lage ist aus der mit dem Mikrophon detektierten Druckänderungen (also die Änderungen des Tones) mittels FFT[5] (Fast Fourier Transformation) das Frequenzspektrum des detektierten Tones zu ermitteln. Dazu wurde die Software Spectrum Lab (Freeware, [1]) benutzt, mit der sehr gute Ergebnisse erzielt wurden.
Bei der Software (nebenstehend ist ein Bild dieser Software) wird im Hauptfenster mittels eines Farbcodes angezeigt, welche Frequenzen wie stark vorkommen. Diese Verteilung ist über der Zeit abgetragen (die "von oben nach unten" verläuft). In dem Fenster oben wird die Lautstärke der einzelnen Frequenzen angezeigt. Im Allgemeinen für das gerade verarbeitete Tonsegment, wird jedoch mit dem Cursor über eine Stelle des zuletzt verarbeiteten Tones gefahren, so wird die Aufschlüsselung dieses Tones ausgegeben. Auf diese Weise können das Maximum und das Minimum des Tones während der Änderung durch die Schwingung gesucht werden.
Das Programm Spectrum Lab ist in der Lage, Audiodateien zu importieren und zu analysieren. Im Verlauf der Entwicklung des Experiments wurden vielfach Töne mit dem Programm Audacity (ebenfalls Freeware[2]) aufgezeichnet und als .mp3-Datei abgespeichert und anschließend zur Analyse in Spectrum Lab importiert.
Versuchsaufbau
Für das Experiment wird zunächst ein Pendel aufgebaut. An der pendelnden Masse wird die Schallquelle befestigt. Natürlich ist es möglich, einen an einen Funktionsgenerator angeschlossenen Lautsprecher zu verwenden, jedoch bietet sich ein möglichst kabelloser Aufbau an. Zum Beispiel kann ein Smartphone mit einem entsprechenden Programm (im Test: Pro Audio Tone Generator) verwendet werden.
Um die Analyse des Signals möglichst einfach zu machen sollte in dem Programm ein Sinuston gewählt werden und kein aus mehreren Frequenzen bestehender Ton.
In einer Linie mit der Pendelbewegung wird, auf den Versuchsaufbau gerichtet, ein Mikrofon aufgebaut, das an einen Computer mit geeigneter Software-Ausstattung angeschlossen ist.
Auf dem Computer wird eine Software zur Analyse des Frequenzspektrums eines akustischen Signals benötigt (hier Spectrum Lab).
Durchführung
Während das Signal vom Sender konstant emittiert wird, wird das Pendel ausgelenkt. Für eine optimale Messung des Effektes sollte dabei darauf geachtet werden, dass das Pendel bestenfalls von oben gesehen parallel zu einer gedachten Geraden durch das Mikrofon und der Aufhängung des Pendels ausgelenkt wird und, dass der Sender grob in die Richtung des Mikrofons zeigt.
Oftmals beginnt der pendelnde Körper, leicht zu rotieren. Ein Effekt dessen Minimierung angestrebt werden sollte, nötigenfalls durch mehrfache Durchführung des Versuches.
Das Pendel und das Mikrofon sollten so aufgestellt (beziehungsweise ausgelenkt) werden, dass die pendelnde Masse dem Mikrofon nicht zu nahe kommt. Einerseits dient das dem Schutz des Mikrofons, welches nicht mit dem Pendel kollidieren sollte, andererseits können bei zu geringem Abstand durch die vom Pendel verdrängte Luft Störgeräusche im Mikrofon entstehen.
Der Ton wird nun, je nach verwendetem Programm, entweder mit dem Programm Spectrum Lab direkt verarbeitet oder mit dem Programm Audacity zunächst aufgenommen und später mit dem anderen beschriebenen Programm verarbeitet.
Zusätzlich kann die Schwingungsdauer mit der Stoppuhr ermittelt werden. Es bietet sich an, die benötigte Zeit für mehrere Schwingungen zu messen und anschließend durch die Anzahl der Schwingungen zu teilen um die Unsicherheit der Messung zu verringern.
Beobachtungen
Betrachtet man das Frequenzspektrum der unbewegten Schallquelle sieht man ein Maximum, das der emittierten Frequenz entspricht (je nach Ausgangssignal kann es sich auch um mehrere Maxima handeln).
Bewegt sich die Schallquelle jedoch relativ zum Empfänger, so kann eine Verschiebung dieses Maximums festgestellt werden. Dabei kann registriert werden, dass sich die Frequenz bei einer Bewegung der Schallquelle und des Empfängers auf einander zu nach oben verschiebt und bei einer Relativbewegung voneinander weg nach unten.
Je höher der Geschwindigkeitsunterschied ist, desto größer ist auch die Frequenzverschiebung.
Ergebnisse und Auswertung
Bei der Betrachtung des Frequenzspektrums (der Aufnahme) des Tones des sich in einer Pendelbewegung befindlichen Senders sollte eine periodische Frequenzverschiebung deutlich sichtbar sein. Von diesen Frequenzverschiebungen werden das Minimum und das Maximum ermittelt.
Aus der ermittelten Verschiebung der Tonhöhe kann auf die Maximalgeschwindigkeit des Pendels geschlossen werden.
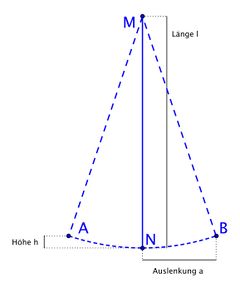
Bei der Emission eines Tones von wurden bei der Auswertung der Aufnahme der Schwingung das Maximum und das Minimum bestimmt. Daraus ergibt sich, nach den Formeln für den Doppler-Effekt, die im folgenden Kapitel Herleitung des Doppler-Effektes hergeleitet wird, für die Geschwindigkeit v bei dem Nulldurchgang (Punkt N in der Abbildung in Theoretischer Hintergrund des Versuches) der Wert .
Mit einer Stoppuhr sind für 3 Schwingungsdauern gemessen worden, daraus ergibt sich . Daraus lässt sich (resultierend aus Herleitung des Doppler-Effektes) die Seillänge berechnen, der gut mit dem gemessenen Wert übereinstimmt, da dieser in dem (relativ kleinen) Intervall der Unsicherheit liegt.
Herleitung des Doppler-Effektes
Für den in diesem Artikel beschriebenen Versuch wird nur die Formel für den Doppler-Effekt für den Fall einer bewegten Schallquelle und eines ruhenden Empfängers benötigt. Die anderen Fälle werden hier deshalb ohne explizite Herleitung angegeben.
Bewegt sich die Schallquelle auf den Empfänger zu, so verkürzt sich die resultierende Wellenlänge des ankommenden Schalls, , um die Distanz , die der Sender in der Zeit einer Schwingung mit der Geschwindigkeit des Senders zurücklegt.
Daraus ergibt sich für die durch den Doppler-Effekt veränderte Wellenlänge unter Ausnutzung der Relation :
Wird unter der Verwendung der gleichen Relation nach der Frequenz umgeformt, so erhält man aus der Gleichung (1) den Zusammenhang
Damit ergibt sich für die durch den Doppler-Effekt verschobene Frequenz :
Bewegt sich die Schallquelle vom Empfänger weg, so verändert sich lediglich das Vorzeichen vor dem Term für die Bewegung der Schallquelle, sodass
für die Wellenlänge und
für die Frequenz gilt.
Ähnlich kann (beispielsweise über die Änderung der Periodendauer durch die Bewegung von Sender und Empfänger auf einander zu) der Doppler-Effekt für einen bewegten Empfänger und eine ruhende Schallquelle berechnet werden und schließlich auch die durch den Doppler-Effekt geänderte Wellenlänge bei bewegtem Empfänger und bewegter Schallquelle (für eine detaillierte Herleitung siehe
[3]).
Für sämtliche Berechnungen wurde angenommen, dass die Schallgeschwindigkeit beträgt. (Dieser Wert wurde nach [6] abgeschätzt.)
| Schallquelle bewegt | Empfänger bewegt | beide in Ruhe |
|---|---|---|
Theoretischer Hintergrund des Versuches
Um die Herleitungen zu diesem Versuch nachzuvollziehen bieten sich die meisten Grundlegenden Werke der Mechanik an (explizit ist hier [7] genutzt worden).
Um die Geschwindigkeit des Senders zu ermitteln wird die Energie des schwingenden Systems in verschiedenen Zeitpunkten zu betrachten.
- Durchläuft das Pendel gerade den Nullpunkt (in der nebenstehenden Abbildung der Punkt N), so verfügt die pendelnde Masse (idealisiert in einem abgeschlossenen System betrachtet) nur über kinetische Energie. Es gilt: .
- In den Punkten maximaler Auslenkung (in der nebenstehenden Abbildung die Punkte A und B) verfügt die pendelnde Masse ausschließlich über potentielle Energie. Es gilt: , wobei h die Höhe der Pendelmasse ist, wie in der Nebenstehenden Abbildung abzulesen ist und die in diesem Kapitel noch hergeleitet wird. Dabei ist die kinetische Energie .
Durch das Gleichsetzen beider Energien (da die Gesamtenergie ja als erhalten angenommen wird) ergibt sich (nach Kürzen) . Somit erhält man für die Geschwindigkeit des Pendels im Punkt N .
Frequenz des Senders bekannt
Für die durch den Doppler-Effekt verringerte Frequenz gilt, wie bereits hergeleitet, , während für die durch den Doppler-Effekt erhöhte Frequenz gilt: .
Daraus folgt, in beiden Fällen, für die Geschwindigkeit des Senders .
Frequenz des Senders unbekannt
Stellt man dann den ersten Ausdruck nach der Geschwindigkeit um () und den zweiten Ausdruck nach , der Ursprungsfrequenz, () und setzt ihn den Ausdruck für ein, so ergibt sich
, ein Ausdruck mit dem die Geschwindigkeit berechnet werden kann, auch wenn die Ursprungsfrequenz unbekannt ist.
Berechnung der Pendelauslenkung und -Höhe
Durch den Satz des Pythagoras geht aus der (rechts) nebenstehenden Abbildung hervor, dass
gilt.
Daraus folgt:.
So kann auch die Höhe der Pendelbewegung errechnet werden. Für diese ergibt sich . (Die zweite Lösung der quadratischen Gleichung ist hier physikalische nicht sinnvoll.)
Berechnung der Seillänge
Für die Länge des Seiles wird die Kreisbewegung des Senders betrachtet, so ergibt sich aus dafür . (Diese fachliche Vereinfachung ist hier möglich, da es sich um die Bewegung in einer Ebene handelt.)
Unsicherheiten
Natürlich sollten im Zuge jeder Durchführung eines Experimentes auch die Unsicherheiten betrachtet werde.
Bei der Durchführung dieses Experimentes können folgende Unsicherheiten betrachtet und bestenfalls minimiert werden:
Unsicherheiten bei
- der Messung der Seillänge (je nach Messmethode, bei einem Büromaßstab können ( gemessene Länge)veranschlagt werden[8])
- der Bestimmung der Frequenzen (der reine Ablesefehler wurde bei der aufgebauten Konfiguration mit (mit gemessene Frequenz) abgeschätzt). Hinzu kommt noch der systematische Fehler, der durch eine Kalibrierung minimiert werden kann)
- der Zeitmessung (je nach Uhr, bei einer Analog-Stoppuhr meist (mit Anzahl des Zeigerumlaufes (also Anzahl gemessener Minuten -1) und gemessene Zeit[9]))
Um die Unsicherheit der Periodendauer möglichst gering zu halten bietet es sich an, die benötigte Zeit für mehrere Schwingungen zu messen und anschließend durch die Anzahl der Schwingungen zu dividieren.
In dem durchgeführten Experiment ergibt sich aus der Länge des Seils plus dem halben Durchmesser der Kugel eine effektive Länge von . Daraus ergibt sich eine Unsicherheit, wie oben beschrieben, von rund .
Die gemessenen Frequenzen befanden sich in dem Bereich von . Die Unsicherheit kann also mit abgeschätzt werden.
Aufgrund der relativ kurzen Zeitmessungen ist der Teil der Unsicherheit der gemessenen Zeit relativ gering und da kein kompletter Zeigerumlauf stattfand entfällt dieser Teil völlig. Mit dem gemessenen Wert von 14,5 Sekunden für 5 Schwingungen ergibt sich eine Unsicherheit von ungefähr , pro Schwingung sogar nur von
Berechnet man jeweils die Auswirkungen der einzelnen Unsicherheiten auf die errechnete Geschwindigkeit , so stellt man fest, dass die Unsicherheit der Frequenzmessung sich am deutlichsten auswirkt, zwei Größenordnungen mehr als die beiden anderen Größen.
Mit Unsicherheiten wurde experimentell (über den Doppler-Effekt) die Geschwindigkeit bestimmt.
Bei dem theoretischen Wert, der Berechnung aus der Kenntnis der Seillänge und der Periodendauer, ergibt sich die Unsicherheit aus den Unsicherheiten eben dieser beider Größen zu .
Alle berechneten, zusammengesetzten Unsicherheiten wurden mittels der in [10] beschriebenen Formel für die Fehlerfortpflanzung ermittelt.
Vergleich der Ergebnisse und Fazit
Bei diesem Experiment wurde experimentell der Wert bestimmt, während der Wert
theoretisch vorhergesagt wurde. Es ist deutlich zu sehen, dass der theoretische Wert innerhalb des Intervalls der Unsicherheit des experimentellen Wertes liegt. Anders herum gilt das leider nicht.
Um präzisere Ergebnisse durch die Messung des Doppler-Effekts zu bekommen, müsste die Auswertungssoftware Spectrum Lab besser kalibriert werden. Auch könnte überprüft werden, ob es eventuell geeignetere Schallquellen gibt als die Verwendete, oder überhaupt deren Güte bestimmt werden.
Alles in allem bietet sich das hier beschriebene Experiment jedoch dafür an, den Doppler-Effekt hör- und messbar im Klassenraum vorzuführen und eine Basis für die Erklärung der zugehörigen Theorie zu bieten.
Literatur
- ↑ Schwarz, O. in: Wissenschaft in die Schulen - PAETEC Verlag für Bildungsmedien Berlin, Frankfurt am Main, Heft 11-03, 2003
- ↑ Hopf, M.; Schecker, H.; Wiesner, H.: Physikdidaktik Kompakt, Aulis Verlag, 1. AuflageS. 106-114, 2011
- ↑ 3,0 3,1 Kircher, E.; Girwidz, R.; Häußler, P.: Physikdidaktik - Theorie und Praxis, Springer, 2. Auflage, S.251, 2009
- ↑ Rahmenlehrplan für die Sekundarstufe I - Jahrgangsstufe 7-10 - Physik, Senatsverwaltung für Bildung, Jugend und Sport Berlin, 2006/2007
- ↑ Brigham, E. O.; Azizi, S. A. : Schnelle Fourier-Transformation, Oldenburg Verlag GmbH, 6. Auflage, München, 1995
- ↑ Dr. Lutz Engelmann ,Formeln und Tabellen f\"ur die Sekundarstufen I und II, Paetec, S. 14, 1996
- ↑ Meschede, D.: Gerthsen Physik, Springer, 24. Auflage, 2010
- ↑ Physikalisches Grundpraktikum, Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik - Mathematisch-Naturwissenschaftliche Fakultät I, Institut für Physik, S. 17, 2007
- ↑ Physikalisches Grundpraktikum, Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik - Mathematisch-Naturwissenschaftliche Fakultät I, Institut für Physik, S. 18, 2007
- ↑ Physikalisches Grundpraktikum, Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik - Mathematisch-Naturwissenschaftliche Fakultät I, Institut für Physik, S. 36, 2007
Siehe auch
Link zur Website des Programmes Spectrum Lab (Freeware).
Link zur Website des Programmes Audacity (Freeware).
Link zu einer Herleitung des Doppler-Effektes auf einer | externen Website.