Der waagerechte Wurf
| Diese Experimentieranleitung befindet sich im Entstehen und wurde noch nicht freigeschaltet..
Solltest du Fragen zu dem Thema haben, nimm am besten Kontakt mit dem Autor auf. |
| Der waagerechte Wurf | |
 Weite eines waagerechten Wurfes | |
| Kurzbeschreibung | |
|---|---|
| Die Verteilung der Weite von Kugel nach einem waagerechten Wurf. | |
| Kategorien | |
| Unterrichtsmaterialien Messunsicherheiten | |
| Einordnung in den Lehrplan | |
| Geeignet für: | Klasse 7, Klasse 8, Klasse 9, Sek. II |
| Sonstiges | |
| Durchführungsform | Schüler*innen-Experiment |
| Anzahl Experimente in dieser Unterkategorie | 2 |
| Anspruch des Aufbaus | leicht |
| Informationen | |
| Name: | F. Boczianowski, L. Pyras |
| Kontakt: | @ |
| Uni: | Humboldt-Universität zu Berlin |
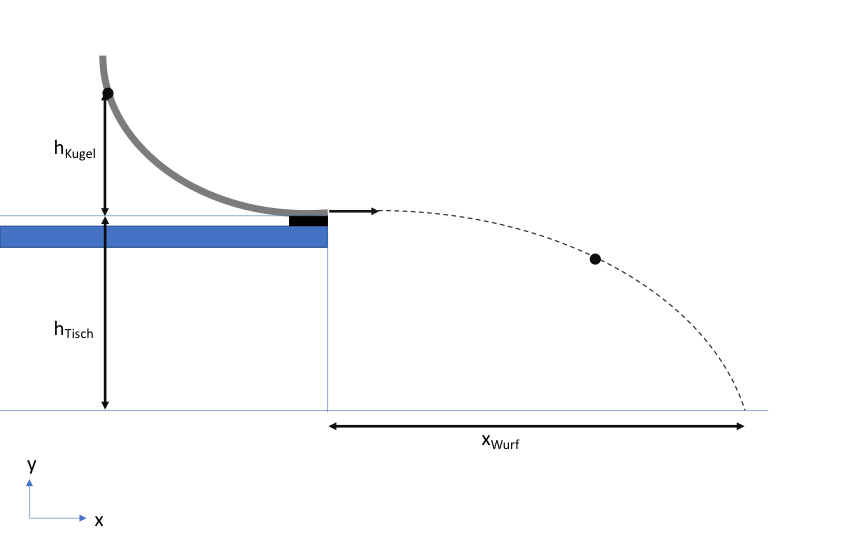
Eine Kugel rollt eine Rampe hinab und verlässt sie in horizontaler Richtung in einer bestimmten Höhe über dem Erdboden. Die Kugel fliegt in einem Bogen und schlägt auf dem Boden in einer bestimmten Weite auf.
Inhaltsverzeichnis
Didaktische Anmerkung
Geräte
Für eine Station:
- gebogene Röhre aus PVC
- Min. 10 Kugeln
- 1 Nagel zum Starten der Kugel
- Zollstock
- Bleistift
- Millimeterpapier
- Kohlepapier
- Klebeband
- evtl. Lot
Aufgabenstellung
Forschungsfrage
Wie weit streuen die Kugeln? (In diesem Fall gibt es keine Hypothese. Es handelt sich um eine sog. Exploration.)
Aufbau
- Befestigen Sie die Kugelrampe auf ihrem Tisch. Verwenden Sie dazu Klemmen und Stativmaterial. (Falls Sie Hilfe benötigen, betrachten Sie das für Ihren Tisch (Sammlung oder Seminarraum) zutreffende Aufbaufoto.)
- Es ist darauf zu achten, dass der Tisch und das Rohr fortan nicht verschoben werden. Arretieren Sie die Bremsen an den Rollen des Tisches.
- Die Kugel lässt sich aus unterschiedlichen Höhen starten, indem die Röhre durch einen Nagel an vorgefertigten Bohrungen verschlossen wird. Testen Sie ihren Aufbau. Sammeln Sie die Kugel unverzüglich ein! Positionieren Sie Millimeterpapier (ohne Durchschlagpapier) an der Stelle der Aufschlagspunkte mit Klebeband auf dem Boden.
- Bestimmen Sie den Abstand vom Ende der Rampe mit Zollstock und Lot mit waagerechter und senkrechter Komponente.
- Präsentieren Sie Ihren Aufbau der Betreuungsperson.
Durchführung
- Führen Sie Messungen für zwei unterschiedliche Höhen durch. Für jede Höhe sind mindestens 30 Wiederholungen sinnvoll.
- Legen Sie Durchschlagpapier auf die erwartete Einschlagstelle. Jede Kugel zeichnet auf diese Weise einen Punkt auf das Millimeterpapier.
- Lesen Sie beide Komponenten der Positionen auf dem Millimeterpapier ab. (Alternativ können Sie die Software engauge-digitizer verwenden, die im PC-Pool verfügbar ist, um aus einem Foto des Millimeterpapiers die Punkte auszulesen. Führen Sie das Experiment dann 2x 50 mal durch.)
- Legen Sie ihre Messung der Betreuungsperson vor.
Auswertung und Ergebnisse
- Erstellen Sie Histogramme für die beiden horizontalen Komponenten der Aufschlagspunkte mit qti für beide Startbedingungen.
- Beschreiben Sie die Verteilung mit eigenen Worten.
- Bestimmen Sie Modalwerte und Mittelwerte. Was unterscheidet die Kennwerte?
- Bestimmen Sie Minima und Maxima, die Standardabweichung und die Standardunsicherheit. Wie unterscheiden sich die Kennwerte? Literaturtipp: Eichler (2016): Das neue Physikalische Grundpraktikum, Kapitel Messen, insbesondere Seite 7, Zufälliger Fehler. Verfügbar unter: https://link.springer.com/chapter/10.1007/978-3-662-49023-5_1 (nur im HU-Netzwerk)
- Tragen Sie in die Histogramme Gauß'sche Glockenfunktionen ein. Benennen Sie Übereinstimmungen und Abweichungen zwischen Histogramm und Glockenfunktion.
- Bestimmen Sie den Bereich, der 68 % ihrer Messwerte einschließt.
- a) Für Ihr Histogramm
- b) Für die Gauß-Funktionen
- Prüfen Sie, …
- a) … ob die Verteilung der Messwerte (68 %-Bereich) symmetrisch um den Mittelwert ist
- b) … ob der 68 %-Bereich Ihrer Messwerte größer oder kleiner als die zweifache Standardabweichung der Gauß-Funktion ist.
Theoretische Modellierung - Aufgabe
Dieser von Ihnen beobachtete Vorgang lässt sich mathematisch unter Verwendung des Konzeptes der Energieerhaltung modellieren. Die Lageenergie der Kugel wird durch die Rampe in Bewegungsenergie überführt, die sich aus der Translation und der Rotation bestimmen lässt. Unberücksichtigt werden: "unruhiger" Lauf der Kugel in der Rampe, Luftreibung und -strömungen.
Aufgabe:
- Überprüfen Sie, wie groß der Einfluss der Rotationsenergie auf die Bewegungsenergie und damit auf die Fallweite der Kugel ist.
- Leiten Sie die mathematische Bestimmung der Flugweiten aus den nachfolgenden Ausgangsgleichungen und Bedingungen her.
- a) Ohne Berücksichtigung der Rotationsenergie
- b) Mit Berücksichtigung der Rotationsenergie
- Bestimmen Sie die Unsicherheiten ihrer berechneten Größen nach dem Verfahren der Größtfehlerabschätzung.
- Vergleichen Sie ihre theoretischen Werte der Flugweite inkl. Größtunsicherheiten mit den gemessenen Weiten inkl. Standardunsicherheiten (für beide Höhen und beide Modelle).
- Beantworten Sie folgende Frage: Welche Schlussfolgerungen ziehen Sie aus diesem Versuch? Welche aus Ihrem Vergleich?
Bewegung der Kugel in horizontaler Richtung nach Verlassen der Rampe:
(1)
(2)
Bewegung der Kugel in senkrechter Richtung:
(3)
(4)
Die Unbekannte lässt sich aus der Energieerhaltung der Kugel berechnen.
Die potentielle Energie beim Start der Kugel beträgt:
(5)
Die kinetische Energie mit Verlassen der Bahn setzt sich aus der Translation und Rotation der Kugel zusammen:
(6)
Wobei das Trägheitsmoment der Kugel ist und ihre Winkelgeschwindigkeit:
(7)
(8)
Theoretische Modellierung - Ausführung
Aus (1) folgt:
In (2) eingesetzt folgt daraus die Wurfparabel:
Zur Bestimmung der Wurfweite ist die Fallzeit zu bestimmen. Also die Zeit, in der die Kugel die Höhe des Tisches durchläuft.
Aus (3) folgt:
Bzw.:
Aus der Energieerhaltung folgt: . Das Trägheitsmoment wird in diese Gleichung eingesetzt.
Es folgt:
Masse und Radius kürzen sich weg:
Daraus folgt die Geschwindigkeit unter Berücksichtigung der Rotationsenergie:
Ohne Rotationsenergie berechnet sich die Geschwindigkeit nach:
Es wird davon ausgegangen, dass die Geschwindigkeitskomponente der z-Richtung durch die feste Bahn in der Röhre vernachlässigbar ist. Somit entspricht diese Geschwindigkeit der Unbekannten .
Die Wurfweite lässt sich also mit:
berechnen.
Ohne Rotationsenergie entspricht die Wurfweite:
Muster
Berechnung der theoretischen Flugweite der Kugel für zwei Messungen
Es findet eine Größtfehlerabschätzung für und statt (Messung mit Lineal bzw. Zollstock), welche im Ergebniswert mit angegeben werden soll.
Vergleich der theoretischen und experimentellen Flugweiten
Die Studierenden sollen zunächst erkennen, dass ihre experimentell ermittelten Werte einer natürlichen Streuung unterliegen, die sich statistisch angeben lässt (Mittelwertberechnung + Konfidenzintervall). Dies kann folgenden Schluss zulassen:
- Es gibt keinen „wahren Wert“.
- Es gibt Wertebereiche, die experimentell ggf. verkleinert werden können.
Diese Ergebnisse sollen Sie nun mit den theoretischen Werten vergleichen, die mit einem Größtfehlerintervall angegeben wurden. Sie erkennen, dass sich die Wertebereiche nicht oder nur geringfügig decken, was diverse Schlüsse zulässt:
- Der Wurf aus geringerer Höhe ist näher am dazugehörigen Theoriewert
- Die mathematische Modellierung ist stets nur eine Näherung ans Experiment
- Das Weglassen vorhandener Einflüsse des experimentellen Aufbaus (Luftreibung, Fallen der Kugel zu Beginn im Rohr, Haftreibung) in der mathematischen Modellierung verdeutlicht diese Näherung
- Die Berücksichtigung der Rotationsenergie liefert ein besseres mathematisches Modell der realen physikalischen Vorgänge als die Vernachlässigung
- …
Es können einige Fragen bezüglich der Sinnhaftigkeit des Versuchs auftauchen. Das Ziel dieses Versuchs ist es, genau für Probleme der Passung von experimentellen und theoretischen Werten sowie der Statistik zu sensibilisieren, kurzum: es gibt in beiden Fällen Faktoren, die es erschweren, Theorie und Experiment (selbst unter Anwendung statistischer Verfahren) in Einklang zu bringen. Eine mögliche Lösung wäre eine kritische Prüfung des experimentellen Aufbaus (z.B. „Schlackern“ der Kugel im Rohr) und/oder eine Überarbeitung der mathematischen Modellierung (z.B. durch Berücksichtigung des Luftwiderstands), um bessere Werte zu erhalten, die aber auch dann immer (!) einer statistischen Streuung unterliegen.
Daten
Ergebnisse
| h_Tisch in m | h_Kugel in m | Berechnete Weite mit Rotation | Berechnete Weite ohne Rotation | Mittelwert der Datenmenge |
|---|---|---|---|---|
| 0,90 | 0,44 | 1,06 | 1,26 | 0,94 |
| 0,90 | 0,26 | 0,82 | 0,97 | 0,78 |
Messwerte
| # | Wurfweite bei h_Kugel=0,44 in m | Wurfweite bei h_Kugel=0,26 in m |
|---|---|---|
| 1 | 0,905 | 0,748 |
| 2 | 0,912 | 0,752 |
| 3 | 0,912 | 0,759 |
| 4 | 0,916 | 0,759 |
| 5 | 0,9165 | 0,761 |
| 6 | 0,9165 | 0,7635 |
| 7 | 0,917 | 0,7645 |
| 8 | 0,925 | 0,7655 |
| 9 | 0,926 | 0,7735 |
| 10 | 0,932 | 0,78 |
| 11 | 0,932 | 0,781 |
| 12 | 0,9315 | 0,781 |
| 13 | 0,9325 | 0,785 |
| 14 | 0,935 | 0,785 |
| 15 | 0,935 | 0,7875 |
| 16 | 0,935 | 0,7875 |
| 17 | 0,9355 | 0,788 |
| 18 | 0,937 | 0,789 |
| 19 | 0,9375 | 0,79 |
| 20 | 0,9405 | 0,79 |
| 21 | 0,941 | 0,791 |
| 22 | 0,9415 | 0,792 |
| 23 | 0,9415 | 0,793 |
| 24 | 0,942 | 0,797 |
| 25 | 0,948 | 0,798 |
| 26 | 0,949 | 0,802 |
| 27 | 0,95 | 0,803 |
| 28 | 0,956 | 0,804 |
| 29 | 0,957 | 0,805 |
| 30 | 0,96 | 0,812 |
| 31 | 0,9605 | 0,8125 |
| 32 | 0,964 | 0,814 |
| 33 | 0,964 | |
| 34 | 0,978 | |
| 35 | 0,9795 |
 Dies ist die
Dies ist die